Open Journal of Discrete Mathematics
Vol.06 No.02(2016), Article ID:65385,10 pages
10.4236/ojdm.2016.62009
On Polynomials 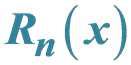 Related to the Stirling Numbers and the Bell Polynomials Associated with the p-Adic Integral on
Related to the Stirling Numbers and the Bell Polynomials Associated with the p-Adic Integral on 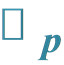
Hui Young Lee*, Cheon Seoung Ryoo
Department of Mathematics, Hannam University, Daejeon, South Korea

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).



Received 29 February 2016; accepted 5 April 2016; published 8 April 2016
ABSTRACT
In this paper, one introduces the polynomials 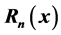 and numbers
and numbers 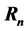 and derives some interesting identities related to the numbers and polynomials:
and derives some interesting identities related to the numbers and polynomials: 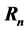 and
and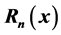 . We also give re- lation between the Stirling numbers, the Bell numbers, the
. We also give re- lation between the Stirling numbers, the Bell numbers, the 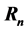 and
and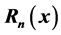 .
.
Keywords:
The Euler Numbers and Polynomials, The Stirling Numbers, The Bell Polynomials and Numbers

1. Introduction
Recently, many mathematicians have studied the area of the Stirling numbers, the Euler numbers and polynomials (see [1] - [11] ). We studied some properties of the polynomials 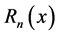 and numbers
and numbers 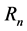 in com- plex field (see [12] ). In this paper, based on the Euler numbers and polynomials, we define the numbers
in com- plex field (see [12] ). In this paper, based on the Euler numbers and polynomials, we define the numbers 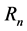 and polynomials
and polynomials 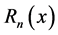 by using the p-adic integrals on
by using the p-adic integrals on 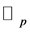 in p-adic field. Then, we get some interesting properties and relations of the Stirling numbers, the
in p-adic field. Then, we get some interesting properties and relations of the Stirling numbers, the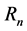 , and the Bell numbers. It is interesting that the Euler polynomials
, and the Bell numbers. It is interesting that the Euler polynomials 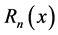 and
and 


Throughout this paper, we use the following notations. By





numbers, 





For
the fermionic p-adic integral on 

If we take 

From (1.2), we obtain

where 
The classical Euler polynomials are defined by the following generating function

with the usual convention of replacing 



But in this paper, Euler numbers are when


The Stirling number of the second kind 

The generating function of the Stirling numbers is defined as below:

As well known definition, the Bell polynomials are defined by Bell (1934) as below

Also, let 

In the special case, 
The motivation of this paper is the Euler numbers and Bell numbers’s generating function. From this idea, we induce some interesting properties related to the Stirling numbers, the Bell numbers, the Euler numbers and the
Our aim in this paper is to define analogue Euler numbers and polynomials. We investigate some properties which are related to



2. An Introduction to Numbers 
Our primary goal of this section is to define numbers 



By (1.2) and using p-adic integral on
Let

Hence, by (2.1) we get the following:

Also, Let

From (2.2) and (2.3), we define numbers and polynomials



respectively.
From above definition, one easily has the Witt’s formula as below:


with the usual convention of replacing 



From (2.6) and
Hence, we get the following;

where 
Also, from (2.5) and by simple calculus, one has

From (2.8) and (2.9), we get some polynomials as below:
3. Basic Properties for 

From (2.5) and by the simple calculation

where 
By comparing the coefficients of 
theorem immediately.
Theorem 1. For 

where 
From (2.5), one has
Let

By comparing the coefficients of 
immediately.
Theorem 2. For 


where 

where 
Also, from (2.1) one has

By comparing the coefficients of 
Theorem 3. For 

Let
Left side of (1.3) is as below:

and right side of (1.3) is as below:

Hence, from (3.4) and (3.5), we get the following theorem.
Theorem 4. For 

where 

By using the definition of 
and the equality above is expressed as follows:
It is well known that


Hence, one has the following theorem.
Theorem 5. For 

where 
By the same method above Theorem 5, we get the corollary as follows:
Corollary 6. For 


where 
It is well known that 

t in the generating function of the Euler polynomials as below:

The left-hand-side of (3.8) is

The right-hand-side of (3.8) is

By (3.9),(3.10) and comparing the coefficient of both sides, we get the following theorem.
Theorem 7. For 

where 

It is not difficult to see that

From the expression (3.11), one has
Specially, if
where 
4. Zeros of the Bell Polynomials 
In this section, we investigate the zeros of the Bell, Euler, and 
From (1.7), we get some polynomials as below:
We plot the zeros of 





Next, we plot the zeros of 







Our numerical results for numbers of real and complex zeros of 

We observe a remarkably regular structure of the complex roots of the Bell polynomials 





Next, we calculate an approximate solution satisfying
Stacks of zeros of 









Since n is the degree of the polynomial







Figure 1. Zeros of
Figure 2. Zeros of


Figure 3. Zeros of


Table 1. Numbers of real and complex zeros of 

Table 2. Approximate solutions of Bn(x) = 0.
zeros 





Acknowledgements
This research was supported by Hannam University Research Fund, 2015.
Cite this paper
Hui Young Lee,Cheon Seoung Ryoo, (2016) On Polynomials Rn(x) Related to the Stirling Numbers and the Bell Polynomials Associated with the p-Adic Integral on 
References
- 1. Rennie, B.C. and Dobson, A.J. (1969) On Stirling Numbers of the Second Kind. Journal of Combinatorial Theory, 7, 116-121.
http://dx.doi.org/10.1016/S0021-9800(69)80045-1 - 2. Abbas, M. and Bouroubi, S. (2005) On New Identities for Bells Polynomials. Discrete Mathematics, 293, 5-10.
http://dx.doi.org/10.1016/j.disc.2004.08.023 - 3. Yang, S.L. (2008) Some Identities Involving the Binomial Sequences. Discrete Mathematics, 308, 51-58.
http://dx.doi.org/10.1016/j.disc.2007.03.040 - 4. Xu, A.-M. and Cen, Z.-D. (2014) Some Identities Involving Exponential Functions and Stirling Numbers and Applications. Journal of Computational and Applied Mathematics, 260, 201-207.
http://dx.doi.org/10.1016/j.cam.2013.09.077 - 5. Kim, T. (2002) q-Volkenborn Integration. Russ. Journal of Mathematical Physics, 9, 288-299.
- 6. Kim, T. (2006) On the Euler Numbers and Polynomials Associated with p-Adic q-Integral on Zp at q = 1. Russian Journal of Mathematical Physics, in Press.
- 7. Kim, T. (2007) q-Euler Numbers and Polynomials Associated with p-Adic q-Integrals. Journal of Nonlinear Mathematical Physics, 14, 15-27.
http://dx.doi.org/10.2991/jnmp.2007.14.1.3 - 8. Kim, T., Choi, J., Kim, Y-.H. and Ryoo, C.S. (2011) A Note on the Weighted p-Adic q-Euler Measure on . Advanced Studies in Contemporary Mathematics, 21, 35-40.
- 9. Kupershmidt, B.A. (2005) Reflection Symmetries of q-Bernoulli Polynomials. Journal of Nonlinear Mathematical Physics, 12, 412-422.
http://dx.doi.org/10.2991/jnmp.2005.12.s1.34 - 10. Ryoo, C.S., Kim, T. and Jang, L.-C. (2007) Some Relationships between the Analogs of Euler Numbers and Polynomials. Journal of Inequalities and Applications, 2007, Article ID: 86052.
- 11. Ryoo, C.S. (2011) A Note on the Weighted q-Euler Numbers and Polynomials. Advanced Studies in Contemporary Mathematics, 21, 47-54.
- 12. Lee, H.Y. and Ryoo, C.S. (2014) On New Polynomials Related to Bell Numbers and Stirling Numbers. Advanced Studies in Theoretical Physics, 8, 763-769.
- 13. Ryoo, C.S. and Kang, J.Y. (2015) A Numerical Investigation on the Structure of the Zeros of Euler Polynomials. Discrete Dynamics in Nature and Society, 2015, Article ID: 174173.
- 14. Ryoo, C.S. (2014) Analytic Continuation of Euler Polynomials and the Euler Zeta Function. Discrete Dynamics in Nature and Society, 2014, Article ID: 568129.
NOTES
*Corresponding author.




























