Open Journal of Discrete Mathematics
Vol.3 No.3(2013), Article ID:34511,6 pages DOI:10.4236/ojdm.2013.33025
Dirichlet Regions and Perfect Codes in Additive Channel
BIT Group, Moscow, Russia
Email: garib@firmbit.ru
Copyright © 2013 Garib Movsisyan. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 13, 2013; revised April 15, 2013; accepted May 17, 2013
Keywords: Dirichlet Regions; Perfect Codes; Additive Channel
ABSTRACT
In the present work, the class of metrics connected with subsets of the linear space on the field, GF(2), is considered and a number of facts are established, which allow us to express the correcting capacity of codes for the additive channel in terms of this metrics. It is also considered a partition of the metric space, Bn, by means of D-representable codes. The equivalence of D-representable and the perfect codes in the additive channel is proved.
1. Introduction
We consider the additive channel of communication [1-4] as a transformer of information, which is a generalization of the classical binary channel with limited number of distortions, 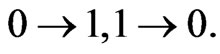 Many notions and facts in the present work take their origins in the classic coding theory and are the direct analogues of the well-known results [1-5].
Many notions and facts in the present work take their origins in the classic coding theory and are the direct analogues of the well-known results [1-5].
The “noise” generated by the additive channel leads to the fact that there appears a word at the outlet of the channel which is different from that at its inlet. In connection with this there rises a necessity of transforming (coding) information for conducting it through the given channel, as well as a necessity of retransforming (decoding) it at the channel outlet. This circumstance makes one introduce such standard notions in the coding theory as: error correcting code; transfer/decoding speed, etc.
On the other hand, as there are many additive channels, the problem of ordering and classification of such channels rises, taking into account the main difficulty, namely, the possibility of correcting the generated errors.
We consider the class of metrics connected with the subsets of the space on the field, GF(2), and establish a number of facts which allow us to express the correcting capacity of codes for the additive channel in terms of this metrics. Also, we consider the partition of the metric space, 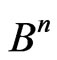 , through
, through  -representable codes. The equivalence of
-representable codes. The equivalence of 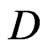 -representable and perfect codes in the additive channel is proved.
-representable and perfect codes in the additive channel is proved.
2. Codes in the Additive Channel
Let 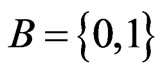 be a Galua field of two elements and
be a Galua field of two elements and 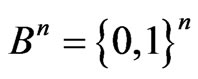 be an n-dimensional vector space on that field.
be an n-dimensional vector space on that field.
If 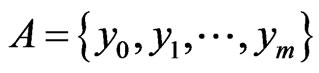 is a subset of
is a subset of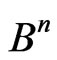 , then the notion of the additive channel is connected with A, as follows.
, then the notion of the additive channel is connected with A, as follows.
Any of the vectors,  , in the channel,
, in the channel,  , is transformed into one of the following vectors:
, is transformed into one of the following vectors:

where  is the operation of addition (with respect to mod 2) in the space,
is the operation of addition (with respect to mod 2) in the space,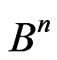 .
.
Definition [1]. For any vector,  , we call the neighbourhood of order t with respect to C, the following set:
, we call the neighbourhood of order t with respect to C, the following set:
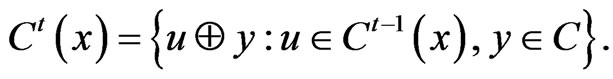
For convenience we take,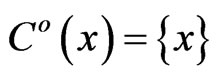 .
.
Examples:
1) Let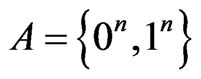 . Then
. Then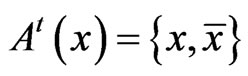 , where
, where 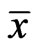 is the logic negation of
is the logic negation of .
.
2) If  is the parity counter, then:
is the parity counter, then:
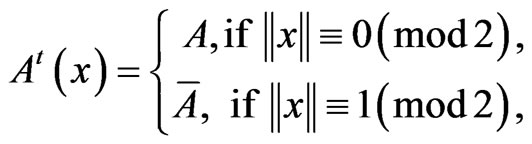
where 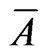 is complement of the set,
is complement of the set, 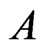 , in
, in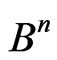 .
.
3) If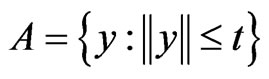 , then in the additive channel,
, then in the additive channel,  , can occur no more than t ‘errors’ of the form,
, can occur no more than t ‘errors’ of the form, 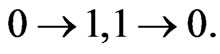 Consequently,
Consequently, 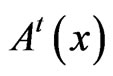 is a sphere of the radius, t, having its centre at the point, x.
is a sphere of the radius, t, having its centre at the point, x.
Thus, we get the classical case of the binary channel with limited number of errors.
Definition [2]. The code, 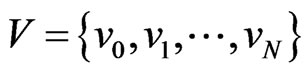 , corrects the errors of the additive channel,
, corrects the errors of the additive channel,  , if:
, if:
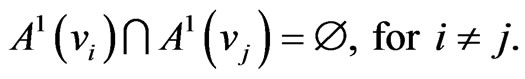
An equivalent form of this condition is:

or the one symmetrical to it:
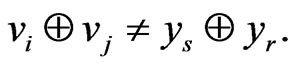
It is obvious that the preceding definitions are symmetric with respect to the pair, 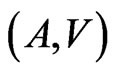 , and therefore, both “generation” and “correction” of errors have the same nature.
, and therefore, both “generation” and “correction” of errors have the same nature.
Statement 1 [3]. If the code, 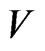 , corrects the errors of the additive channel,
, corrects the errors of the additive channel, 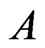 , then the code,
, then the code, 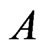 , corrects the errors of the additive channel,
, corrects the errors of the additive channel,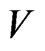 .
.
To describe the “relations” of the additive channel, 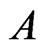 , and the code,
, and the code, 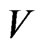 , correcting the errors of that channel it is convenient to introduce the following double-case predicate,
, correcting the errors of that channel it is convenient to introduce the following double-case predicate,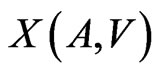 :
:

Definition. We call any pair, 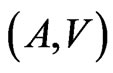 , additive if it is a solution of the following equation:
, additive if it is a solution of the following equation:
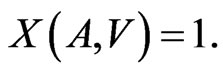
Taking this definition into account, the property of perfectness of codes can be written as follows:
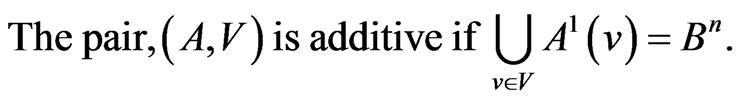
Note that there are as many additive channels, as there are Boolean functions, and a few of them do not essentially differ from each other. It is not clear how to classify such channels yet, but the following statements correspond the commonly accepted viewpoint.
Definition [3]. The channels, A and C, are called equivalent if any code correcting the errors of the additive channel, A, corrects the errors of the channel, C, and vice versa.
Introducing the following relation of partial order, one can formally write:
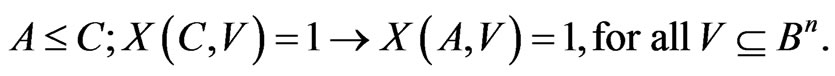
If , then
, then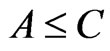 , which is natural.
, which is natural.
This property makes possible to look additive channels with the ‘best’ and ‘worst’ correcting capacities for each 
Statement 2 [3]. The additive channels, 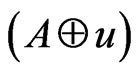 and
and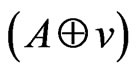 , are equivalent for any
, are equivalent for any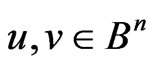 .
.
Statement 3 [3]. If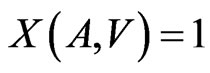 , then
, then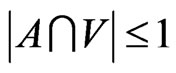 .
.
It follows from the preceding statements that one can consider—without loss of generality:
a) If  is a class of additive channels equivalent to
is a class of additive channels equivalent to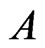 , then it is sufficient to solve the coding problem for any representative of that class.
, then it is sufficient to solve the coding problem for any representative of that class.
b) The additive channel, 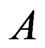 , includes the null vector, which can be interpreted as the possibility of errorless transfer of the signal through that channel.
, includes the null vector, which can be interpreted as the possibility of errorless transfer of the signal through that channel.
As it follows from 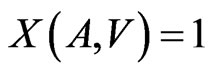 that
that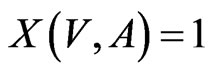 , then an analogical statement is correct for the vector,
, then an analogical statement is correct for the vector, 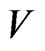 , too, i.e. it is sufficient to discuss the codes including the null vector.
, too, i.e. it is sufficient to discuss the codes including the null vector.
Thus, it follows from 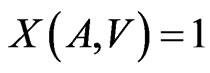 that the sets,
that the sets, 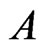 and
and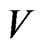 , can overlap only at zero, and the search of the code,
, can overlap only at zero, and the search of the code, 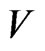 , is to be organized in the set,
, is to be organized in the set,  Below:
Below:
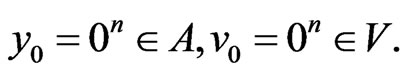
As the power of the neighbourhood of order t does not depend on the vector,  , we make the following denotation,
, we make the following denotation, 
Note that for the additive pair, 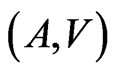 , the following limits take place [2]:
, the following limits take place [2]:
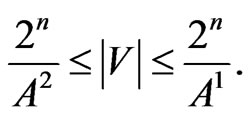
It is clear that the upper limit is reached for the perfect pair, 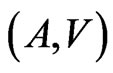
3. Metrics and Codes
The standard and most used metrics in coding theory is Hamming’s metrics, i.e. the following function:
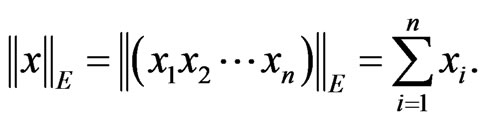
One can consider that this metrics is connected with the “natural” basis, 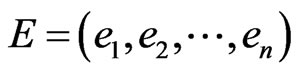 , in the following way:
, in the following way:

It is obvious that if another basis, 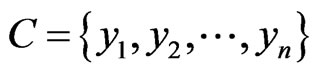 , is chosen then another metrics is generated:
, is chosen then another metrics is generated:
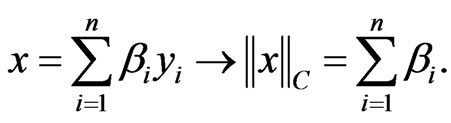
The more general procedure of metrics generation in the above-mentioned way is as follows. For the given subset, 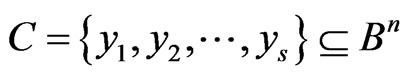 , and the given vector,
, and the given vector, 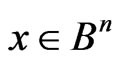 , we consider all expansions of x with respect to
, we consider all expansions of x with respect to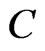 , i.e. the expansions having the following form:
, i.e. the expansions having the following form:
 (1)
(1)
and then we put the following number into correspondence with the above expansion:
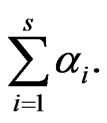
Then, choosing the least of these numbers, we define the following norm (the MLM norm) connected with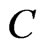 :
:

Lemma 1 [4]. The function,  , is a metrics (below, MLM metrics) for any subset,
, is a metrics (below, MLM metrics) for any subset,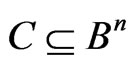 .
.
Example:
4) If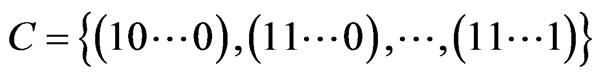 , the MLM norm has the following form:
, the MLM norm has the following form:
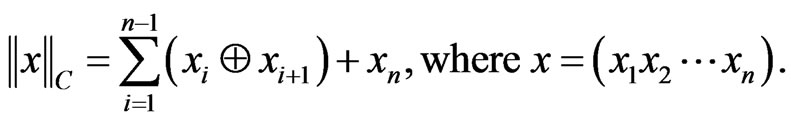
In particular, for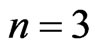 , the MLM norms of vectors in
, the MLM norms of vectors in 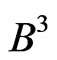 take the following values:
take the following values:
In terms of graph theory, the above situation is as follows. We give the following binary relation on the set of vortices, :
:
This relation defines adjacency and, geometrically, the set of vortices of the N-dimensional unit cube corresponds to the metrical space, 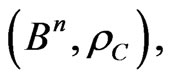 and the distance between two points in
and the distance between two points in 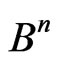 is equal to the minimum number of sides in the circuit connecting the corresponding vortices, or it is infinity, if there is no such circuit.
is equal to the minimum number of sides in the circuit connecting the corresponding vortices, or it is infinity, if there is no such circuit.
Let 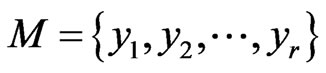 be a basis for the additive channel, A. We consider any basis,
be a basis for the additive channel, A. We consider any basis,  , in the space,
, in the space, 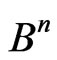 , where
, where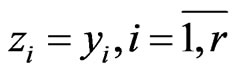 , and f is a linear reversible transformation,
, and f is a linear reversible transformation, 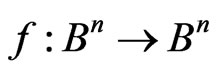 , defined in the following way:
, defined in the following way:

We denote the image of the set, 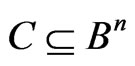 , by
, by :
:

It is obvious that if , then
, then  for all
for all .
.
We denote the linear shell of the set, 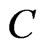 , by
, by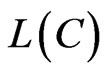 , and we denote by
, and we denote by 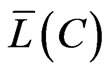 the subset in
the subset in 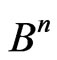 satisfying the following condition:
satisfying the following condition:
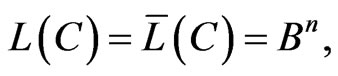
where + means the direct sum the subspaces. It is obvious that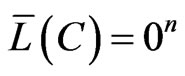 , if
, if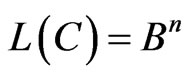 .
.
The following holds true.
Lemma 2 [4]. For any vectors, 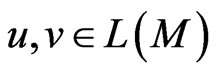 , the following relations hold true:
, the following relations hold true:
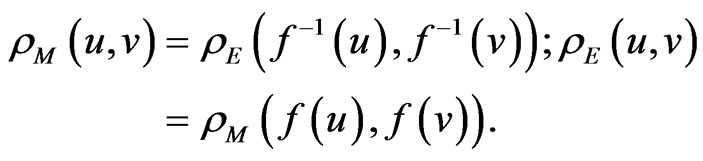
Lemma 3 [6]. The code, 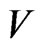 , corrects the errors of the additive channel, А, iff the following holds true:
, corrects the errors of the additive channel, А, iff the following holds true:
Example:
5) We consider the channel,
 , as an illustration. “Physically”, the channel A means that the “errors” of the form,
, as an illustration. “Physically”, the channel A means that the “errors” of the form, 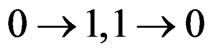 , which take place either in the 1st place, or in the 1st and 2nd places simultaneously, and so on. Thus,
, which take place either in the 1st place, or in the 1st and 2nd places simultaneously, and so on. Thus,  and to build a maximum volume code correcting the errors of the given channel we use Lemma 3. It is sufficient to consider all the subsets,
and to build a maximum volume code correcting the errors of the given channel we use Lemma 3. It is sufficient to consider all the subsets, 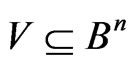 , for which:
, for which:
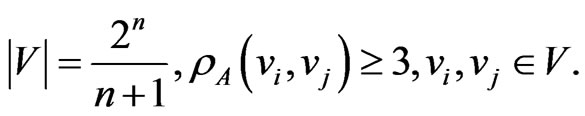
Let 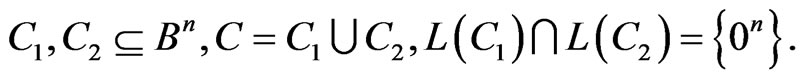
Lemma 4. For any 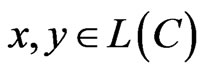 holds true the equation:
holds true the equation:
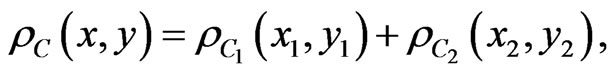
where .
.
Proof. It follows from the conditions of lemma that the vectors, 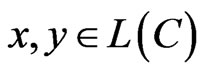 , are one to one represented in the form [7]:
, are one to one represented in the form [7]:
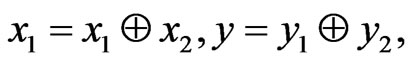 where
where .
.
Consequently:
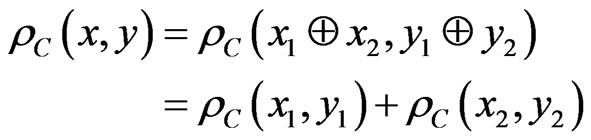 (2)
(2)
We assume—without loss of generality—that:
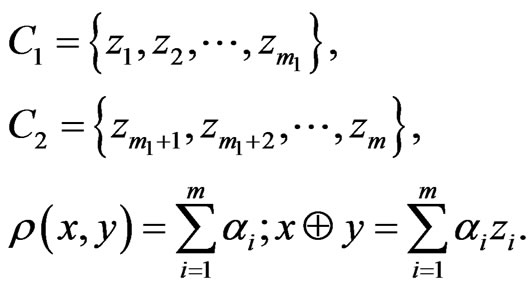
Then:
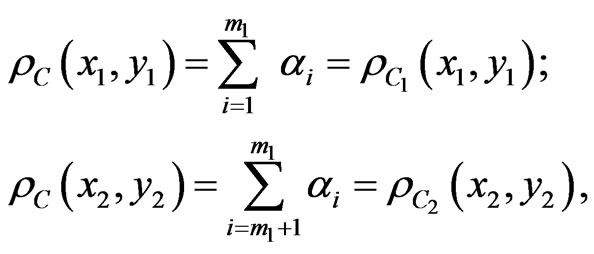
where:
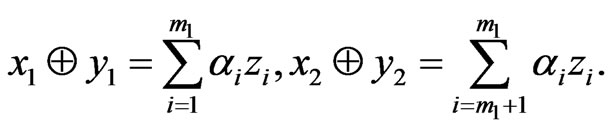
Consequently, taking (2) into account, we get:
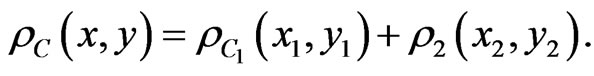
Q.E.D.
Lemma 5. For any additive pairs, 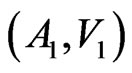 and
and
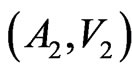 , where
, where  the pair,
the pair,
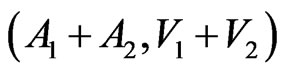 , is additive, too.
, is additive, too.
Proof. Let for 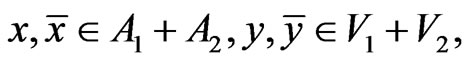 hold the following equation:
hold the following equation:
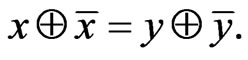 (3)
(3)
From the definition of the direct sum of sets it follows that:

where 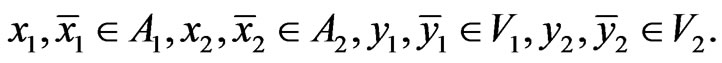
Consequently, taking (3) into account, we get:
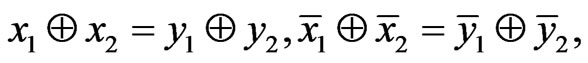
That is, the pairs,  and
and  are not additive.
are not additive.
Q.E.D.
4. Partition of the Metric Space into Dirichlet’s Regions
Let 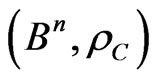 be the metric space with an MLM norm,
be the metric space with an MLM norm, 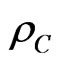 , where
, where 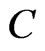 is a subset in
is a subset in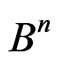 .
.
We define for any 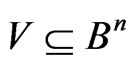 the Dirichlet region,
the Dirichlet region,  , of the point,
, of the point, 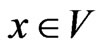 , in the following way:
, in the following way:

It is obvious that:
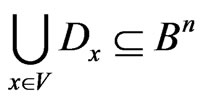 (4)
(4)
In fact, Dirichlet’s region of the point,  , includes all points of the metric space,
, includes all points of the metric space, 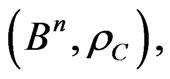 which are not farther from
which are not farther from 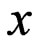 than from the other points in
than from the other points in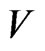 .
.
It is easy to notice that it is sufficient given the coincidence of the sets, 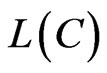 and
and , for (4). Nevertheless, this condition is not always necessary, which can be seen from the following example.
, for (4). Nevertheless, this condition is not always necessary, which can be seen from the following example.
Examples:
6) Let
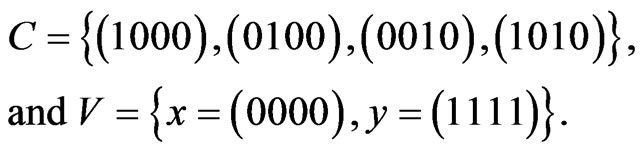
Then we have:
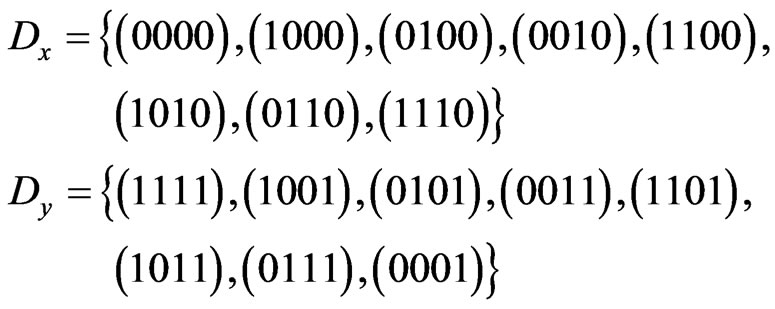
that is, 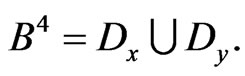
7) Let
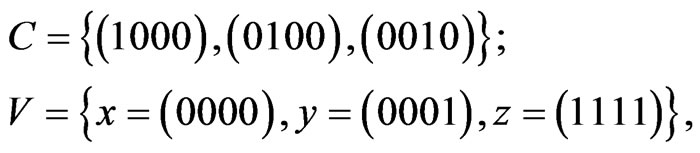
then:
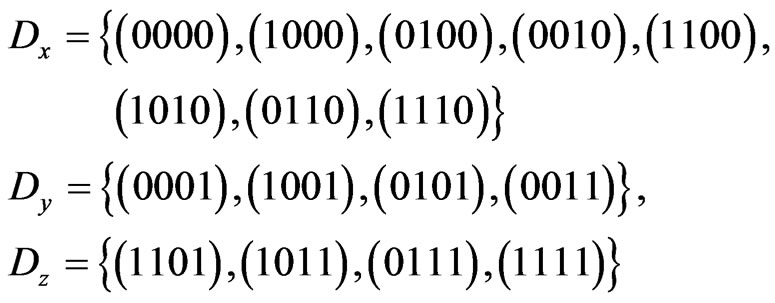
It is obvious that: 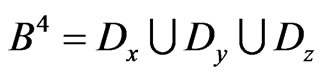 and
and 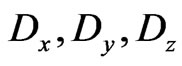 do not overlap in pairs. It follows from this example that the condition,
do not overlap in pairs. It follows from this example that the condition,  , or
, or  is not necessary for the equality (4).
is not necessary for the equality (4).
The following theorem ‘connects’ 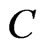 and
and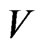 , giving the answer to the question: which are the conditions providing Equation (4).
, giving the answer to the question: which are the conditions providing Equation (4).
Theorem 2. The equation:
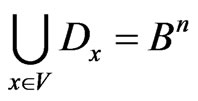
holds true for all 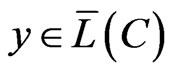 iff:
iff:
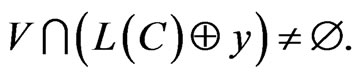
Proof. Taking (4) into account, it is sufficient to prove that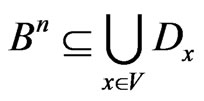 , i.e. for every vector,
, i.e. for every vector,
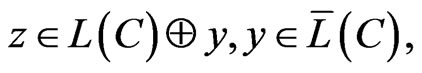 there is such
there is such 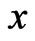 that
that . As for any vectors,
. As for any vectors, 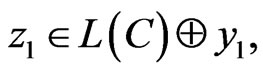
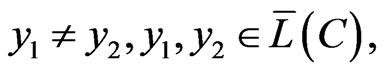
 holds the following:
holds the following:
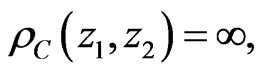
then  iff
iff 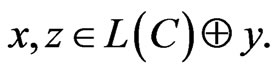
Q.E.D.
Definition. The code,  , is called
, is called  -representable in the metrical space,
-representable in the metrical space, 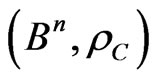 , if all Dirichlet regions of the points in
, if all Dirichlet regions of the points in 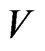 do not overlap in pairs.
do not overlap in pairs.
We note that D-representability of a code is connected with a certain metrics and, in general, this property does not preserve if the metrics is changed.
Example:
8) Let:
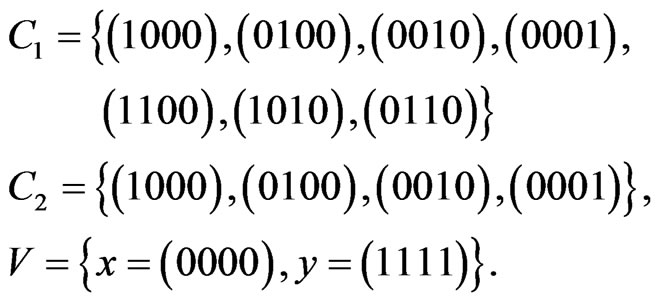
We have in the metric space, 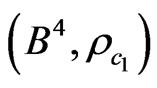 that
that
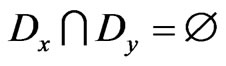 . But
. But 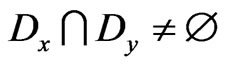 in the metric space,
in the metric space,

Theorem 3. The code, 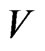 , is D-representable in the metrical space,
, is D-representable in the metrical space, 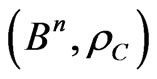 , iff the code,
, iff the code, 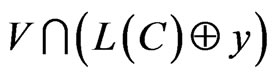 is D-representable in the metrical space,
is D-representable in the metrical space, 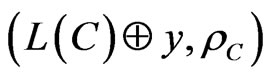 , for all
, for all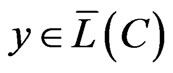 .
.
Proof. For 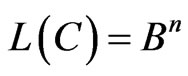 we have:
we have:

then it is logical to consider the case, 
Necessity. Let the code, 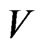 , be D-representable in
, be D-representable in 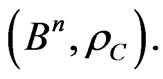 Then the following holds true: for every vector,
Then the following holds true: for every vector, 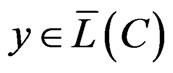 , the vector,
, the vector,  belongs only to one Dirichlet region,
belongs only to one Dirichlet region, 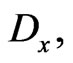 where
where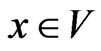 . Then, according to Theorem 2, we have that
. Then, according to Theorem 2, we have that
 Consequently, the code,
Consequently, the code,
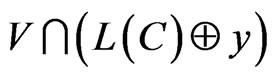 , is D-representable in
, is D-representable in .
.
Sufficiency. Let 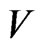 be not D-representable in
be not D-representable in
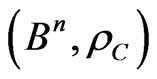 . Then there is such vector,
. Then there is such vector, 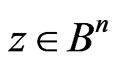 , that
, that
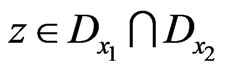 , where
, where
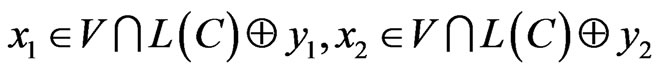 , and
, and
 . The following cases are possible:
. The following cases are possible:
a) 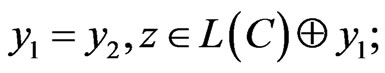
b) 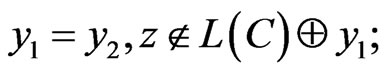
c) 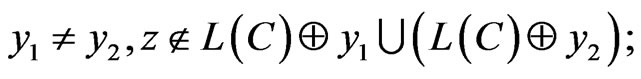
d) 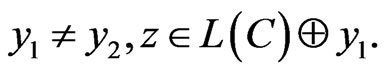
It is not difficult to prove with these that in the space,
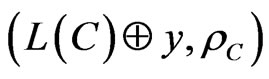 , including the vector,
, including the vector,  , the code,
, the code,
 , is not D-representable, which is a contradiction. Q.E.D.
, is not D-representable, which is a contradiction. Q.E.D.
This theorem can be formulated in another way.
Corollary. The metric space, 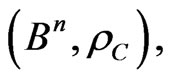 is partitioned into Dirichlet’s regions of the points of the code,
is partitioned into Dirichlet’s regions of the points of the code, 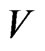 , iff the metric space,
, iff the metric space, 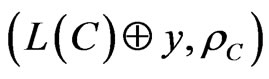 , is partitioned into Dirichlet’s regions of the points,
, is partitioned into Dirichlet’s regions of the points,
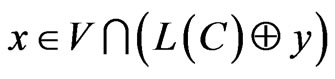 , for all
, for all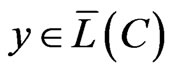 .
.
We describe the algorithm of building the code, 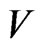 , partitioning the metric space,
, partitioning the metric space, 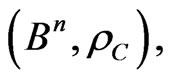 into Dirichlet’s regions.
into Dirichlet’s regions.
Step 1. We choose an arbitrary code, 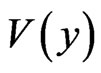 , from the space,
, from the space,  , partitioning the metric space,
, partitioning the metric space,
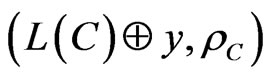 , into Dirichlet’s regions for which
, into Dirichlet’s regions for which
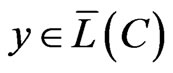 .
.
Step 2. The code obtained through the formula:
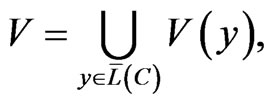
partitions the metric space,  into Dirichlet’s regions.
into Dirichlet’s regions.
Let  any basis of the channel,
any basis of the channel, .
.
Theorem 4. If the code,  , is
, is 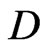 -representable in the metric space,
-representable in the metric space, 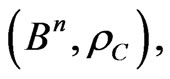 then the additive pair,
then the additive pair, 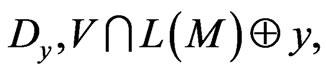 is perfect for
is perfect for .
.
Proof. It follows from Theorem 3 that the code,
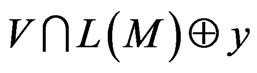 , is
, is 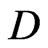 -representable in
-representable in
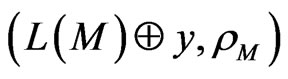 . As M is a basis for
. As M is a basis for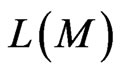 , then it follows from Theorem 4 [8] (taking Lemma 2 and Lemma 3 into account) that the code,
, then it follows from Theorem 4 [8] (taking Lemma 2 and Lemma 3 into account) that the code, 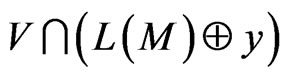 , is perfect in
, is perfect in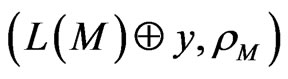 . Applying Lemma 3 and Lemma 4, we get that the additive pair,
. Applying Lemma 3 and Lemma 4, we get that the additive pair,
 , is perfect for every vector,
, is perfect for every vector,
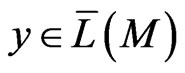 .
.
Q.E.D.
Nevertheless, we note that the perfectness of the additive pairs:
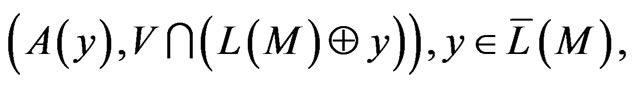
is not a sufficient condition for 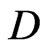 -representability of the code,
-representability of the code, 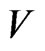 , in
, in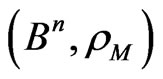 , though
, though  is a basis for all
is a basis for all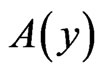 .
.
Example:
9)
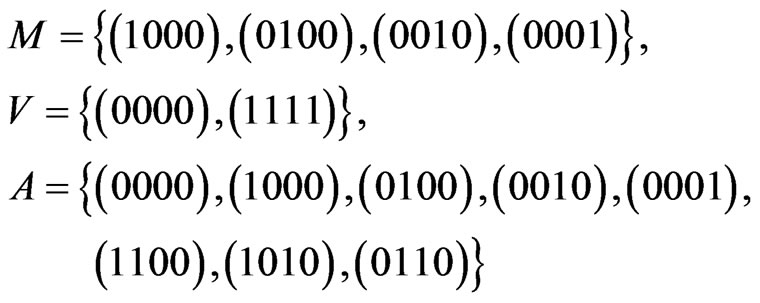
The code, 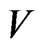 , is
, is 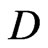 -representable in
-representable in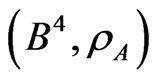 , but it is not
, but it is not 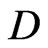 -representable in
-representable in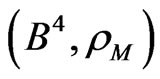 , though the additive pair,
, though the additive pair, 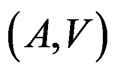 , is perfect in
, is perfect in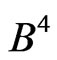 .
.
Theorem 5. If the additive pair,  is perfect, then V is
is perfect, then V is 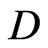 -representable in the metric space,
-representable in the metric space, 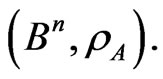
Proof. As 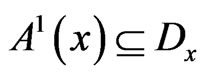 for every vector,
for every vector, 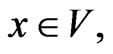 and
and
 , then
, then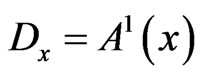 . On the other handfrom perfectness of the code, V, it follows that the set,
. On the other handfrom perfectness of the code, V, it follows that the set, 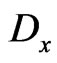 , for all
, for all 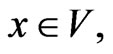 disjoints. That is, V is D-representable.
disjoints. That is, V is D-representable.
Corollary. The additive pair, ( is perfect if the metric space,
is perfect if the metric space, 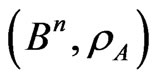 , is partitioned by the Dirichlet’s regions,
, is partitioned by the Dirichlet’s regions, 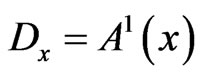 , of the points,
, of the points, 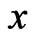 , from
, from .
.
Thus, we reduced the problem of building the perfect Pair, 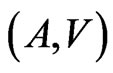 to the problem of
to the problem of 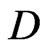 -representability of the code,
-representability of the code,  , in the metric space,
, in the metric space, 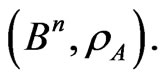
REFERENCES
- V. K. Leontyev and G. L. Movsisyan, “On the Additive Channel of Communication,” Reports of Academy of Sciences of Armenia, Vol. 104, No. 1, 2004, pp. 23-27.
- V. K. Leontyev, G. L. Movsisyan and J. G. Margaryan, “Perfect Codes in Additive Channels,” Reports of RAS, Vol. 411, No. 3, 2006, pp. 306-309.
- V. K. Leontyev, G. L. Movsisyan and J. G. Margaryan, “On Perfect Codes in Additive Channels,” Problems of Information Communication, Vol. 44, No. 4, 2008, pp. 12-19.
- V. K. Leontyev, G. L. Movsisyan and J. G. Margaryan, “Codes in Additive Channels,” Report of the Academy of Sciences of Armenia, Vol. 110, No. 4, 2010, pp. 334-339.
- F. J. M. Williams and N. J. A. Sloane, “The Theory of Error-Correcting Codes,” Bell Laboratories, Marray Hill, 1977.
- V. K. Leontyev, G. L. Movsisyan and J. G. Margaryan, “Correction of Errors in the Additive Channel,” Vestnik RAU, Vol. 2, No. 1, 2010, pp. 12-25.
- Yu. M. Movsisyan, “Higher Algebra and Number Theory,” Yerevan State University, Yerevan, 2008, p. 455.
- V. K. Leontyev, G. L. Movsisyan and J. G. Margaryan, “Partition of N-Dimensional Space on GF(2) into Dirichlet’s Regions,” Vestnik RAU, Vol. 2, No. 1, 2011, pp. 26-41.

