Open Journal of Discrete Mathematics
Vol.2 No.1(2012), Article ID:17157,11 pages DOI:10.4236/ojdm.2012.21006
On the Line Graph of the Complement Graph for the Ring of Gaussian Integers Modulo n
1Department of Mathematics, Irbid National University, Irbid, Jordan
2Department of Mathematics, Palestine Technical University (Kadoorie), Tulkarm, Palestine
Email: dr_mghanem@yahoo.com, k.nazzal@ptuk.edu.ps
Received October 13, 2011; revised November 2, 2011; accepted November 22, 2011
Keywords: Complement of a graph; Chromatic index; Diameter; Domination number; Eulerian graph; Gaussian integers modulo n; Hamiltonian graph; Line graph; radius; Zero divisor graph
ABSTRACT
The line graph for the complement of the zero divisor graph for the ring of Gaussian integers modulo n is studied. The diameter, the radius and degree of each vertex are determined. Complete characterization of Hamiltonian, Eulerian, planer, regular, locally  and locally connected
and locally connected 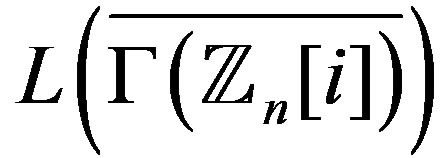 is given. The chromatic number when
is given. The chromatic number when 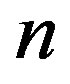 is a power of a prime is computed. Further properties for
is a power of a prime is computed. Further properties for 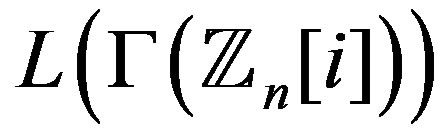 and
and 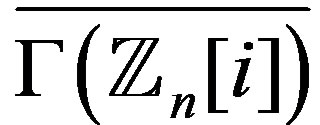 are also discussed.
are also discussed.
1. Introduction
The line graph 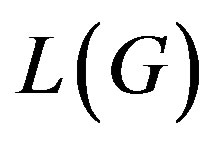 of a graph
of a graph 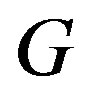 is defined to be the graph whose vertex set constitutes of the edges of
is defined to be the graph whose vertex set constitutes of the edges of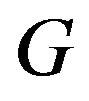 , Where two vertices are adjacent if the corresponding edges have a common vertex in
, Where two vertices are adjacent if the corresponding edges have a common vertex in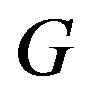 . The importance of line graphs stems from the fact that the line graph transforms the adjacency relations on edges to adjacency relations on vertices. For example, the chromatic index of a graph leads to the chromatic number of its line graph. The zero divisor graph of a commutative ring
. The importance of line graphs stems from the fact that the line graph transforms the adjacency relations on edges to adjacency relations on vertices. For example, the chromatic index of a graph leads to the chromatic number of its line graph. The zero divisor graph of a commutative ring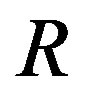 , denoted by
, denoted by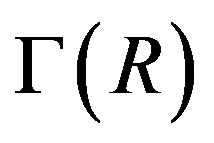 , is defined as the graph whose vertex set is the set of all non-zero zero divisors of
, is defined as the graph whose vertex set is the set of all non-zero zero divisors of 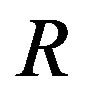 and edge set
and edge set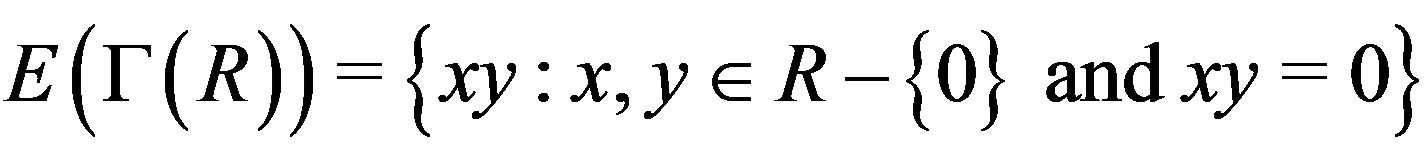 . This type of graphs provides an example showing that algebraic methods could be applied to problems about graphs. The set of Gaussian integers, denoted by
. This type of graphs provides an example showing that algebraic methods could be applied to problems about graphs. The set of Gaussian integers, denoted by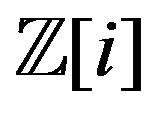 , is defined as the set of complex numbers
, is defined as the set of complex numbers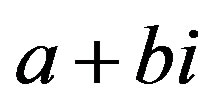 , where
, where 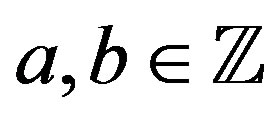 . If
. If  is a prime Gaussian integer, then
is a prime Gaussian integer, then 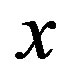 is either 1)
is either 1) 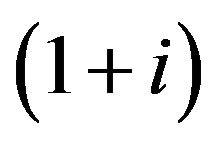 or
or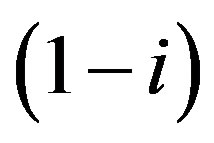 , or 2) q where q is a prime integer and
, or 2) q where q is a prime integer and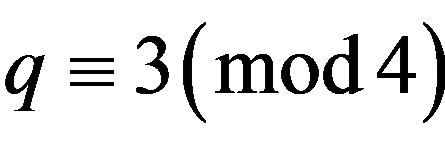 , or 3)
, or 3)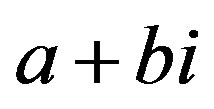 ,
, 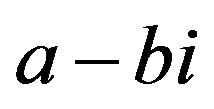 where
where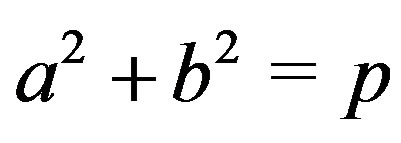 ,
, 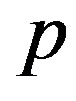 is a prime integer and
is a prime integer and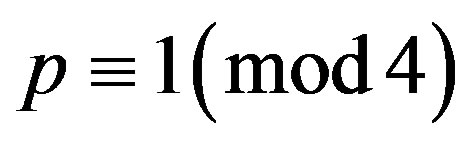 .
.
Throughout this paper, 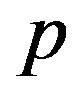 and
and 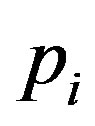 denote prime integers which are congruent to 1 modulo 4, while
denote prime integers which are congruent to 1 modulo 4, while 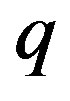 and and
and and 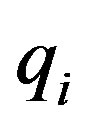 denote prime integers which are congruent to 3 modulo 4. All rings in this paper are assumed to be commutative with unity. The zero divisor graph for the ring of Gaussian integers modulo
denote prime integers which are congruent to 3 modulo 4. All rings in this paper are assumed to be commutative with unity. The zero divisor graph for the ring of Gaussian integers modulo 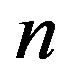 is studied in [1] and [2], the complement of this graph is discussed in [3]. While the line graph of the zero divisor graph for the ring of Gaussian integers modulo n is investigated in [4]. In this paper it should be kept in mind that
is studied in [1] and [2], the complement of this graph is discussed in [3]. While the line graph of the zero divisor graph for the ring of Gaussian integers modulo n is investigated in [4]. In this paper it should be kept in mind that
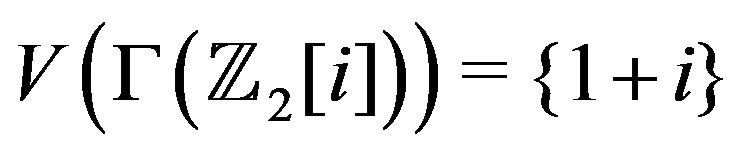 , and hence, its line graph is
, and hence, its line graph is ,
,
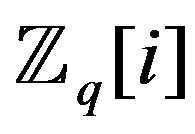 is an integral domain, so
is an integral domain, so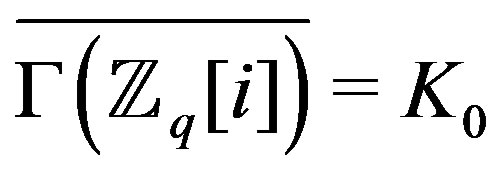 . Further,
. Further,
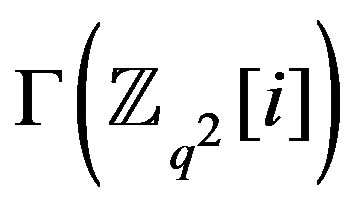 is a complete graph whose complement is totally disconnected and thus its line graph is
is a complete graph whose complement is totally disconnected and thus its line graph is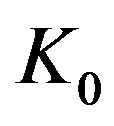 . While
. While
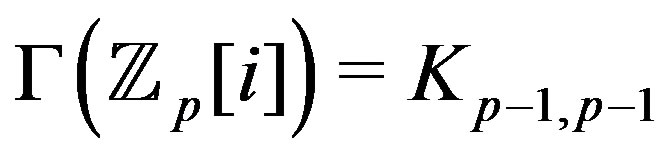 , so its complement is disconnected with two components each of which is isomorphic to
, so its complement is disconnected with two components each of which is isomorphic to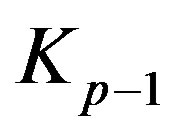 . Finally, note that the graph
. Finally, note that the graph 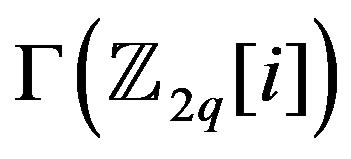 is bipartite, [1] and
is bipartite, [1] and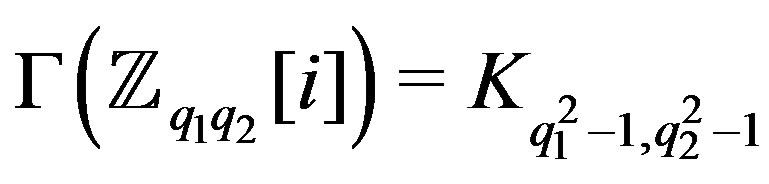 .
.
In this paper, we investigate properties of the graph
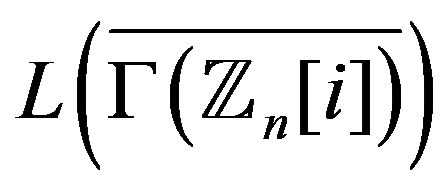 . We find the diameter, the radius of
. We find the diameter, the radius of
 . We determine which
. We determine which 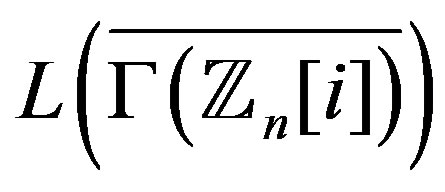 is Eulerian, Hamiltonian, regular, locally
is Eulerian, Hamiltonian, regular, locally , locally connected or planer. Furthermore, the chromatic index and the edge domination number of
, locally connected or planer. Furthermore, the chromatic index and the edge domination number of 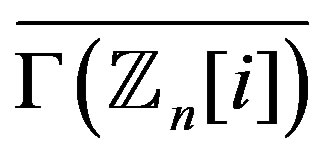 where
where  is a power of a prime are computed. While the domination number of
is a power of a prime are computed. While the domination number of 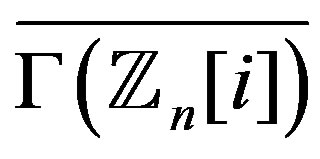 is given. On the other hand, a formula which gives the degree of each vertex in
is given. On the other hand, a formula which gives the degree of each vertex in 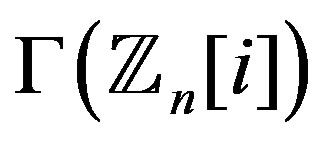 is derived, thus the degree of its complement as well as its line graph could easily be found.
is derived, thus the degree of its complement as well as its line graph could easily be found.
2. When Is 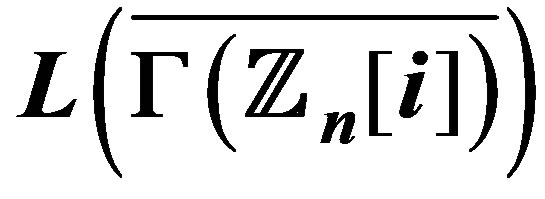 Eulerian or Planner
Eulerian or Planner
If 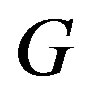 is a connected graph. Then
is a connected graph. Then 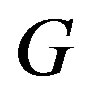 is Eulerian if and only if every vertex of
is Eulerian if and only if every vertex of 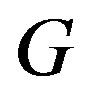 has even degree. For a finite ring
has even degree. For a finite ring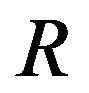 , the line graph
, the line graph 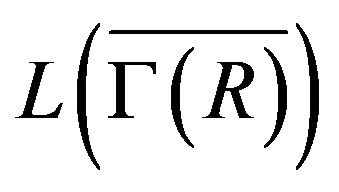 of a connected graph
of a connected graph 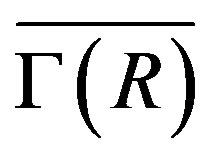 is Eulerian if and only if all vertices of
is Eulerian if and only if all vertices of 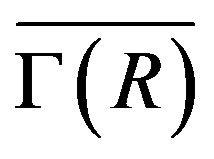 have the same parity ( see the proof of Lemma 3.10, [5]). On the other hand, if
have the same parity ( see the proof of Lemma 3.10, [5]). On the other hand, if 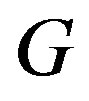 has both even and odd vertices, then so is its complement. So, for a connected graph
has both even and odd vertices, then so is its complement. So, for a connected graph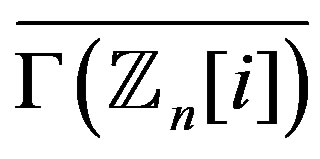 , the graph
, the graph 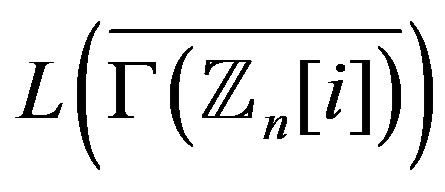 is Eulerian if and only if all vertices in
is Eulerian if and only if all vertices in 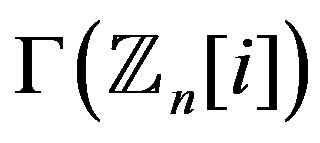 are either even or all vertices in
are either even or all vertices in 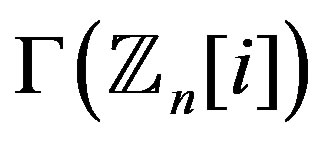 are all odd. But
are all odd. But 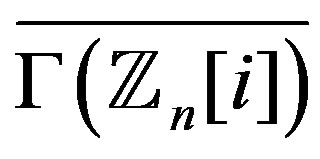 is connected if
is connected if 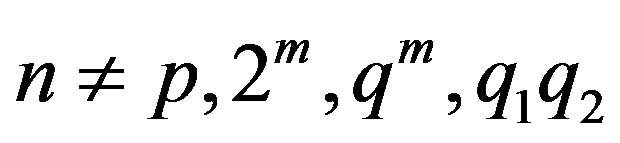 [3] and
[3] and 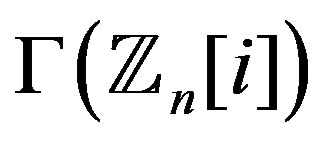 is Eulerian if
is Eulerian if 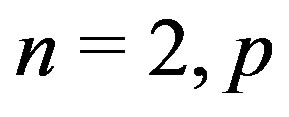 or
or 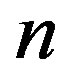 is a product of distinct odd primes [1]. It is easy to show that all vertices of
is a product of distinct odd primes [1]. It is easy to show that all vertices of 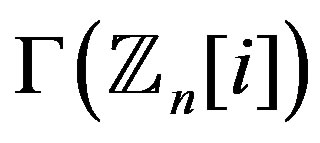 are odd if and only if
are odd if and only if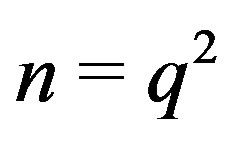 . This proves the following theorem.
. This proves the following theorem.
Theorem 2.1 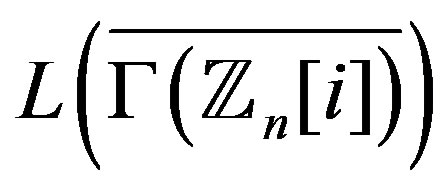 is Eulerian if and only if
is Eulerian if and only if  is a product of distinct odd primes.
is a product of distinct odd primes.
A planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints.
Next we determine when the graph 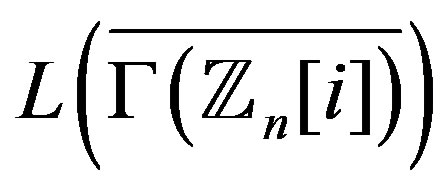 is planar.
is planar.
In a graph 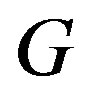 the maximum vertex degree and the minimum vertex degree will be denoted by
the maximum vertex degree and the minimum vertex degree will be denoted by 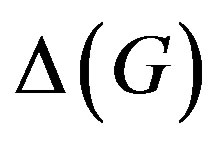 and
and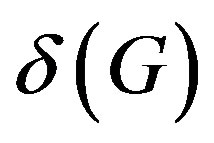 , respectively.
, respectively.
The following theorem characterizes graphs 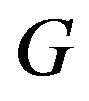 whose line graph
whose line graph 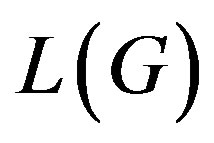 is planer.
is planer.
Theorem 2.2 [6]
A nonempty graph 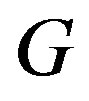 has a planer line graph
has a planer line graph 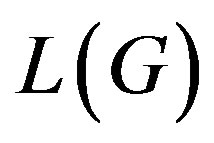 if and only if 1)
if and only if 1) 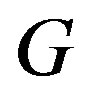 is planer.
is planer.
2)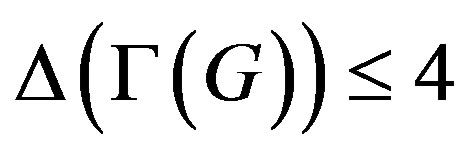 , and 3) if
, and 3) if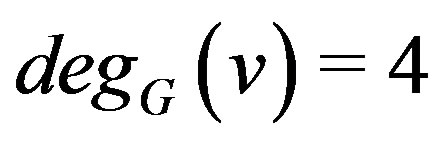 , then
, then  is a cut vertex.
is a cut vertex.
The graph 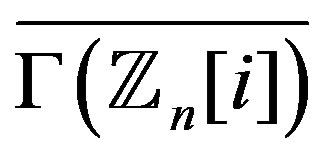 is planer if and only if
is planer if and only if 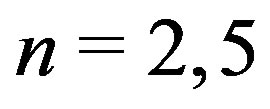
or 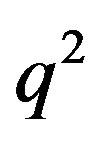 [3]. For
[3]. For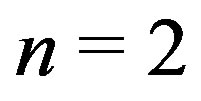 ,
, 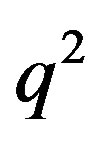 ,
,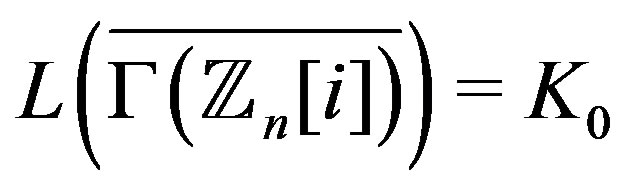 . While for
. While for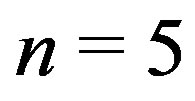 ,
, 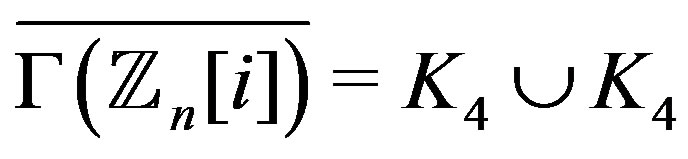 , this graph is regular of degree 3.
, this graph is regular of degree 3.
Thus we obtain the following.
Theorem 2.3 The graph 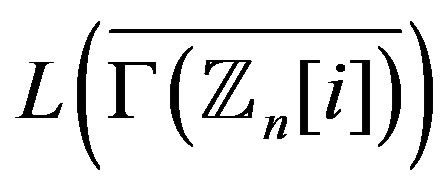 is planer if and only is
is planer if and only is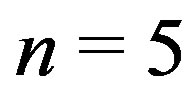 .
.
3. The Diameter of 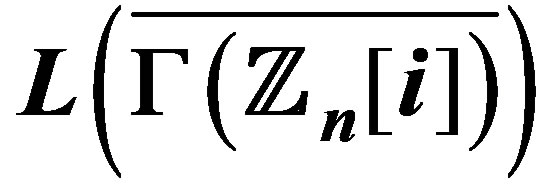
For a connected graph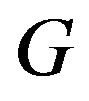 , the distance,
, the distance, 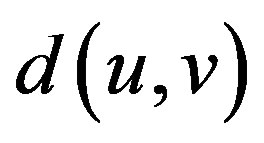 , between two vertices
, between two vertices 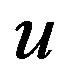 and
and 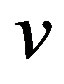 is the minimum of the lengths of all
is the minimum of the lengths of all 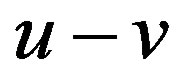 paths of
paths of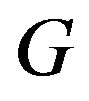 . The eccentricity of a vertex
. The eccentricity of a vertex 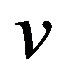 in
in 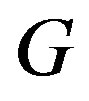 is the maximum distance from
is the maximum distance from 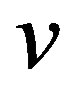 to any vertex in
to any vertex in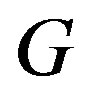 . The diameter of
. The diameter of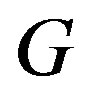 ,
, 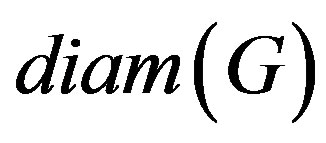 , is the maximum eccentricity among the vertices of
, is the maximum eccentricity among the vertices of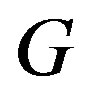 . Since
. Since
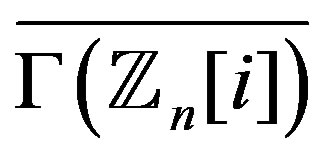 is connected if
is connected if 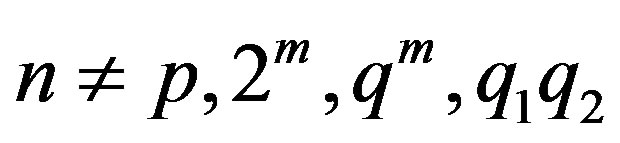 and each of
and each of 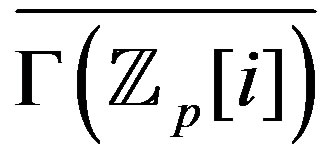 and
and 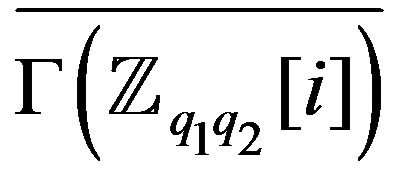 is the union of two complete graphs, while
is the union of two complete graphs, while 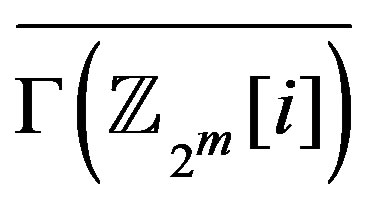 and
and 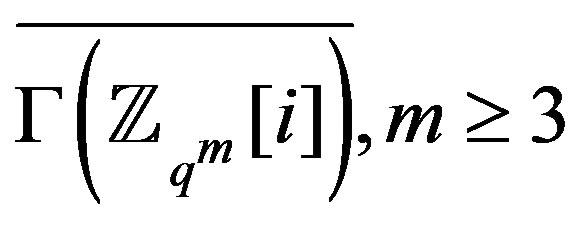 are the union of a nullgraph and a connected graph [3], we have the following.
are the union of a nullgraph and a connected graph [3], we have the following.
Theorem 3.1 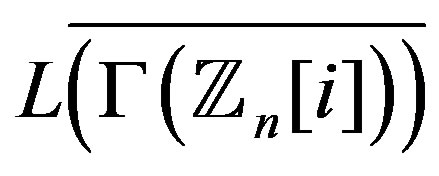 is connected if and only if
is connected if and only if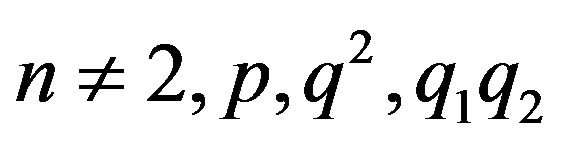 .
.
Theorem 3.2 If 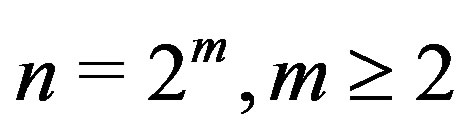 or
or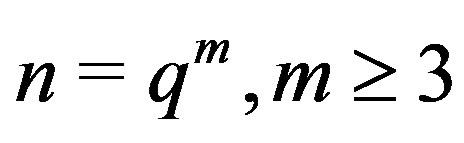 , then
, then
 .
.
Proof. 1) Assume that 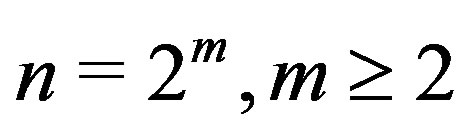 and
and
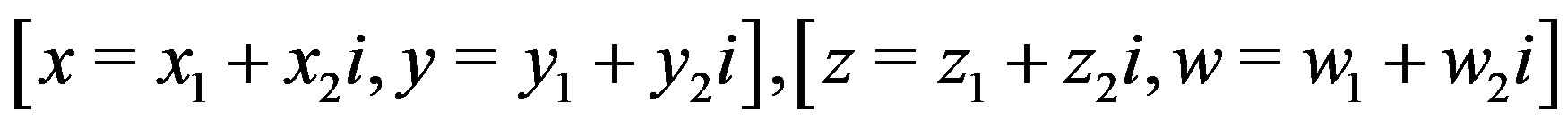
are two nonadjacent vertices in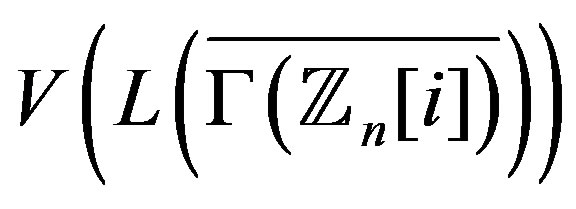 . Since for every
. Since for every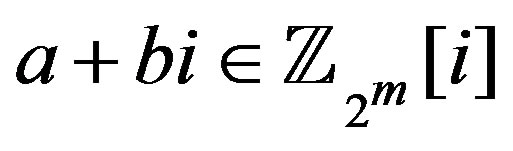 ,
,  and
and  are both even or odd [1], we have three cases:
are both even or odd [1], we have three cases:
Case I: for ,
, 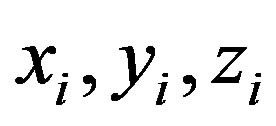 and
and 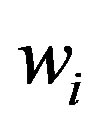 are odd. Then we have the path
are odd. Then we have the path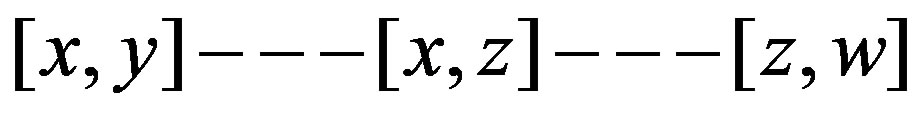 .
.
Case II: for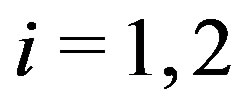 ,
, 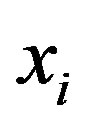 or
or 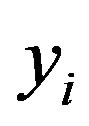 is odd(even) and
is odd(even) and 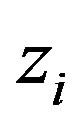 or
or 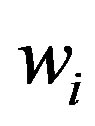 is even (odd). Assume that
is even (odd). Assume that 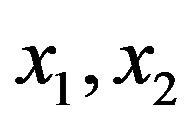 are even and
are even and 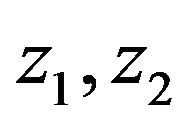 are odd. Then we have the path
are odd. Then we have the path  .
.
Case III: for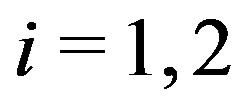 ,
, 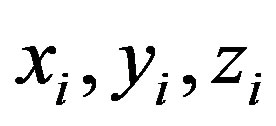 and
and 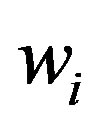 are even.
are even.
Then 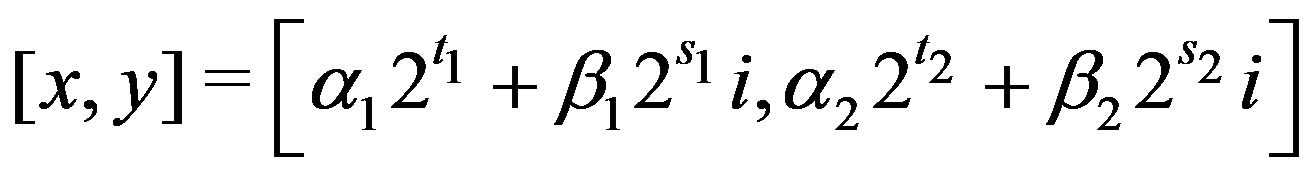 and
and
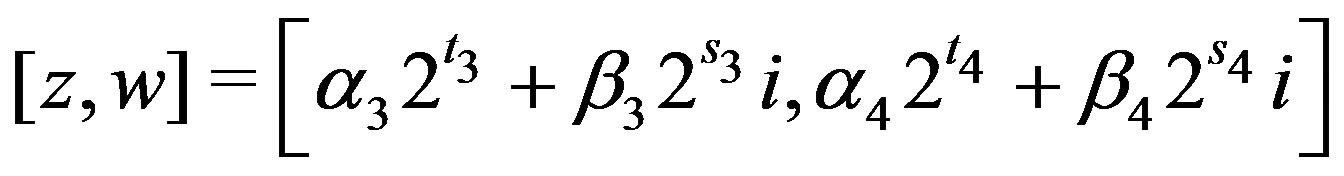 where
where 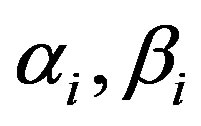
are odd and 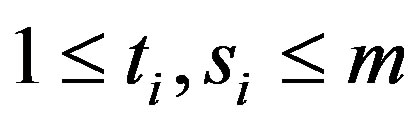 for
for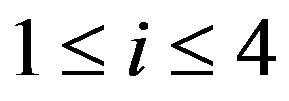 . If
. If 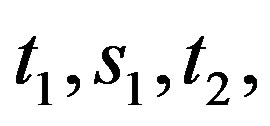 or
or
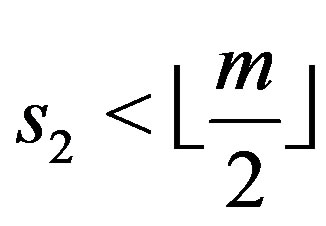 , say
, say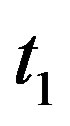 , then
, then 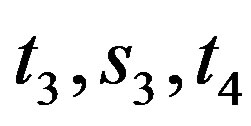 or
or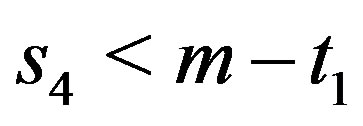 , say
, say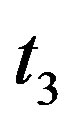 .
.
So, we have the path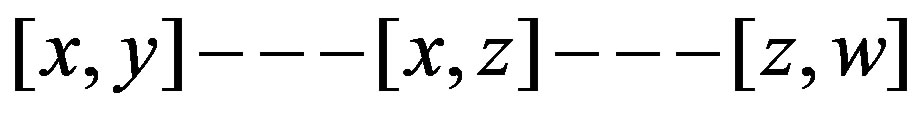 . Now suppose that
. Now suppose that 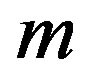 is odd. Then a) If
is odd. Then a) If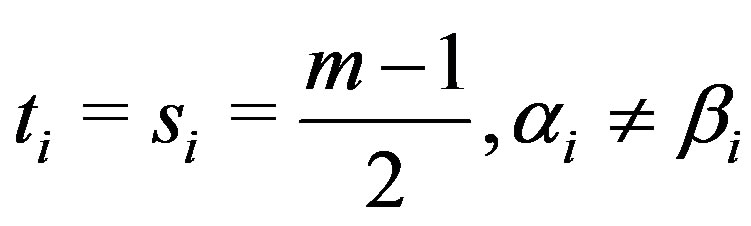 , for
, for 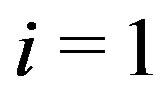 or 2, say for
or 2, say for
 , then
, then 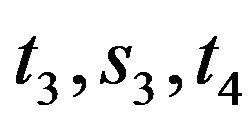 or
or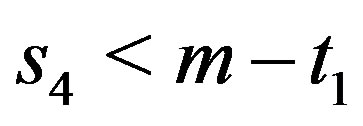 , say
, say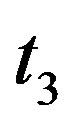 . Hence, we have the path
. Hence, we have the path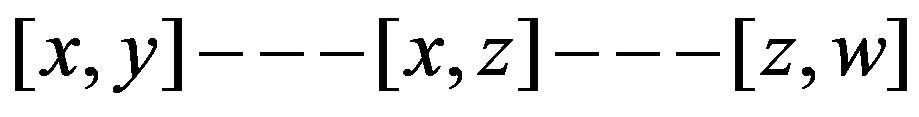 .
.
b) If 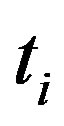 or
or 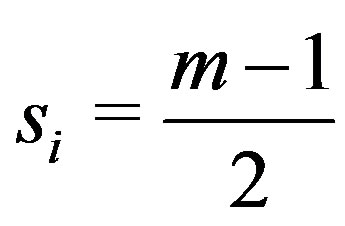 and
and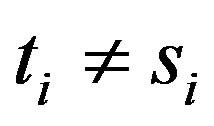 , for
, for 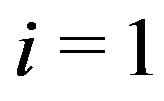 or 2, say for
or 2, say for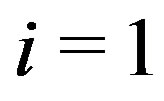 , then we have a path
, then we have a path 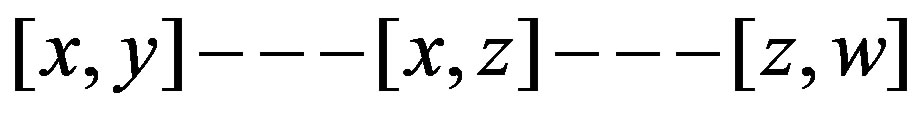 or
or 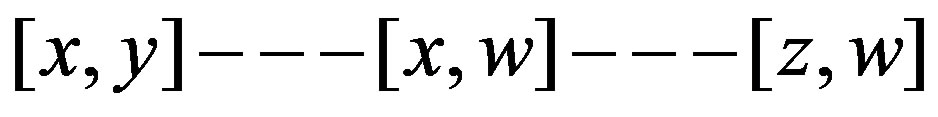 .
.
c) If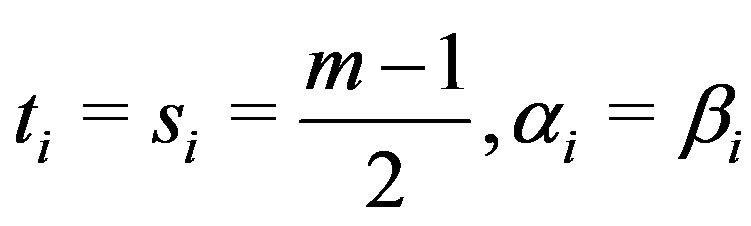 , for
, for 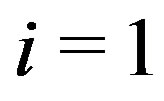 or 2, say for
or 2, say for
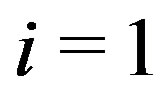 , then
, then 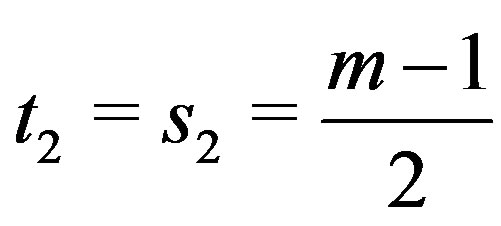 implies that
implies that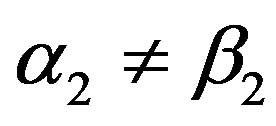 . Otherwise
. Otherwise 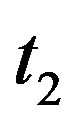 or
or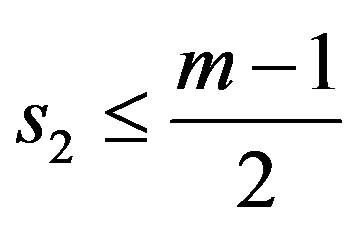 . Then we have a path
. Then we have a path
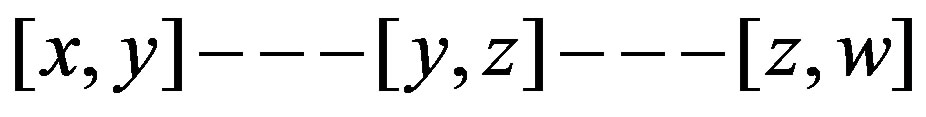 or
or 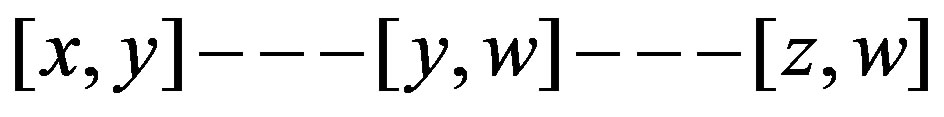 .
.
2) Assume that 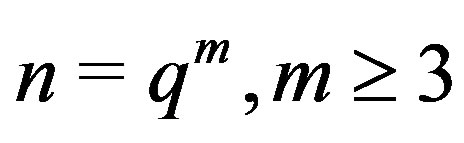 and
and
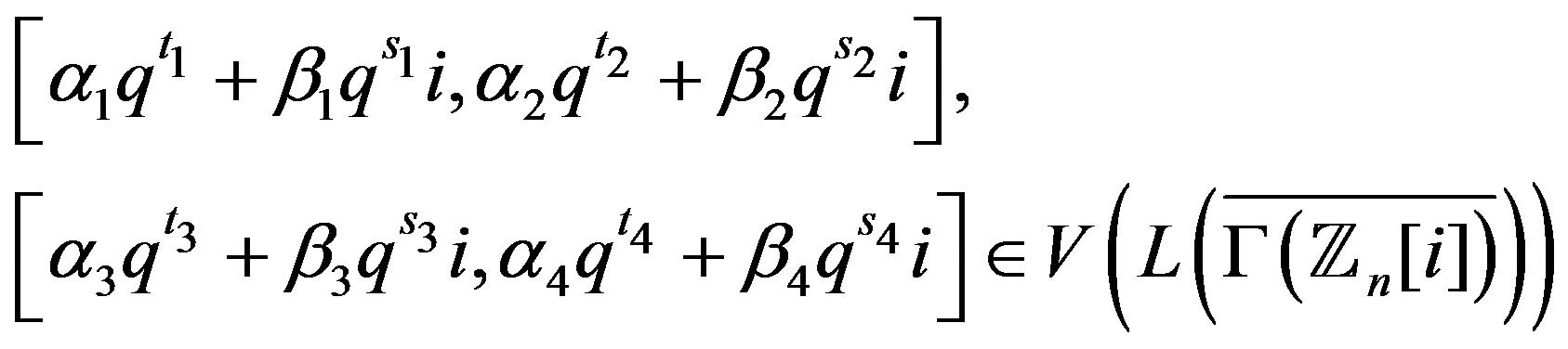
Then 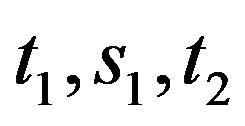 or
or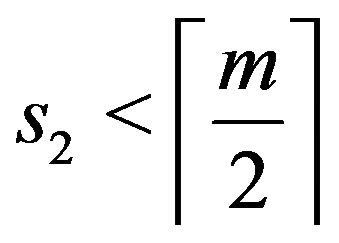 , say
, say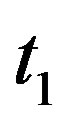 . Hence
. Hence 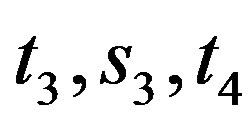 or
or
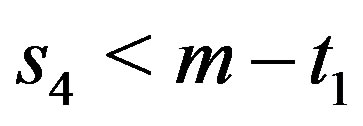 , say
, say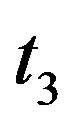 . Then we have the path
. Then we have the path
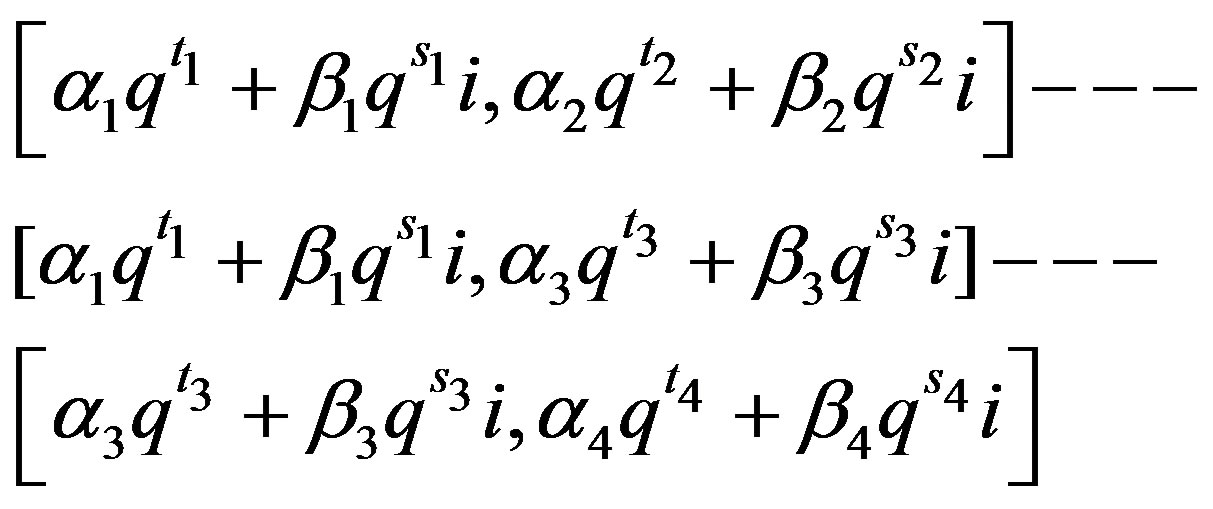 .
. 
Theorem 3.3 Let 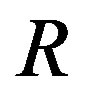 be a ring that is a product of two rings
be a ring that is a product of two rings 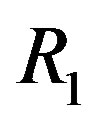 and
and 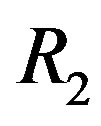 with at least one of them is not ID with more than one regular element and the other has more than two regular elements. Then
with at least one of them is not ID with more than one regular element and the other has more than two regular elements. Then 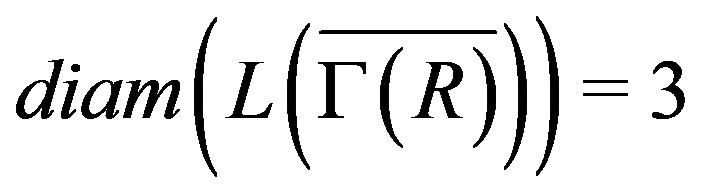 .
.
Proof. Suppose that 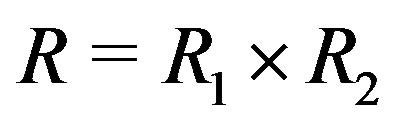 and
and 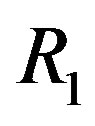 is not ID,
is not ID, 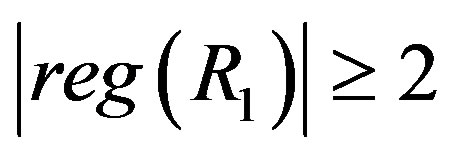 and
and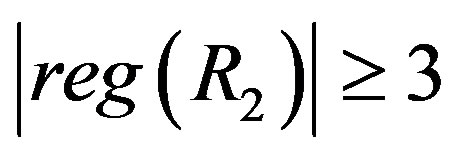 . Let
. Let 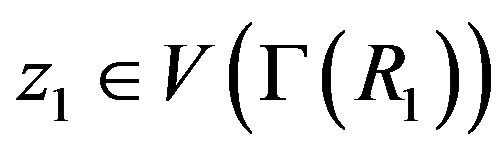 and
and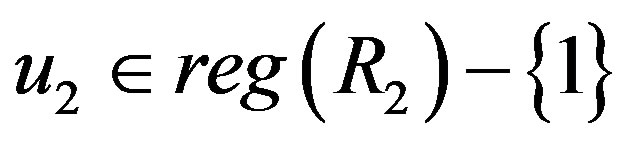 . Clearly,
. Clearly,
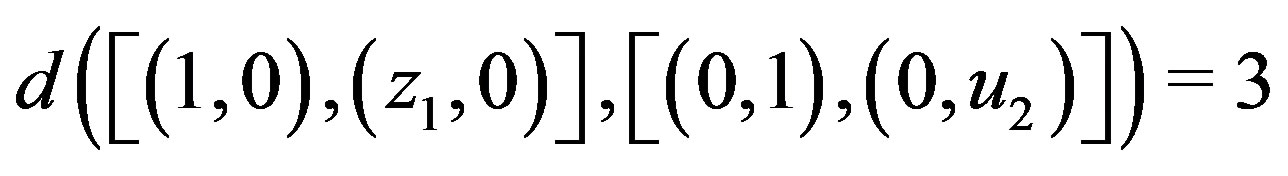 in
in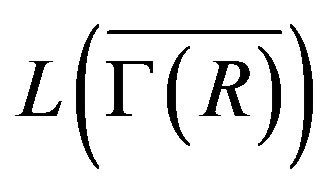 . So,
. So,
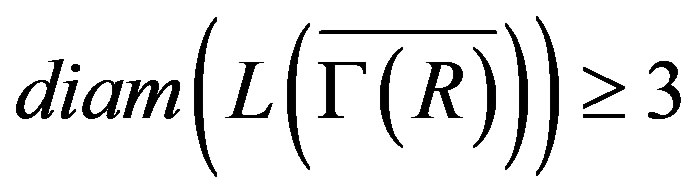 . Now, let
. Now, let
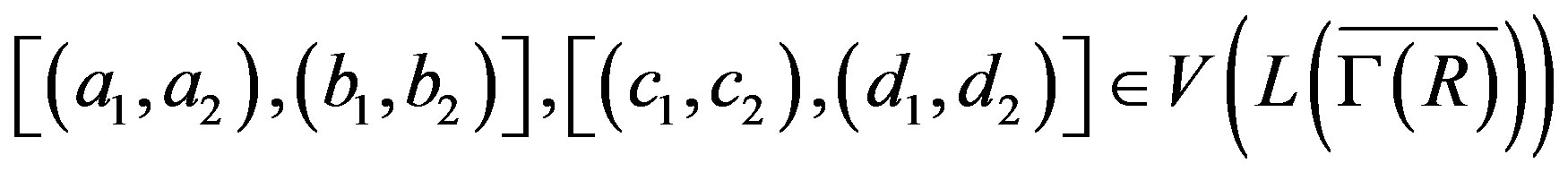 then
then  or
or 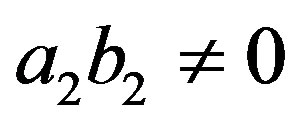 and
and 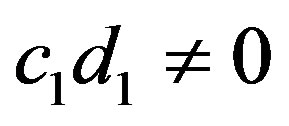 or
or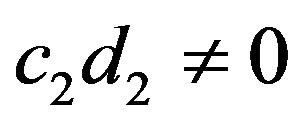 . So, we have three cases:
. So, we have three cases:
Case I: 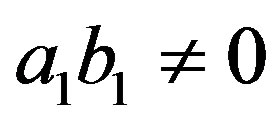 and
and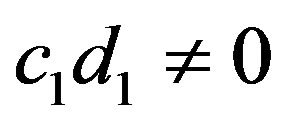 . Then
. Then
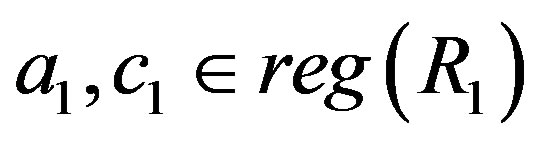 implies that
implies that
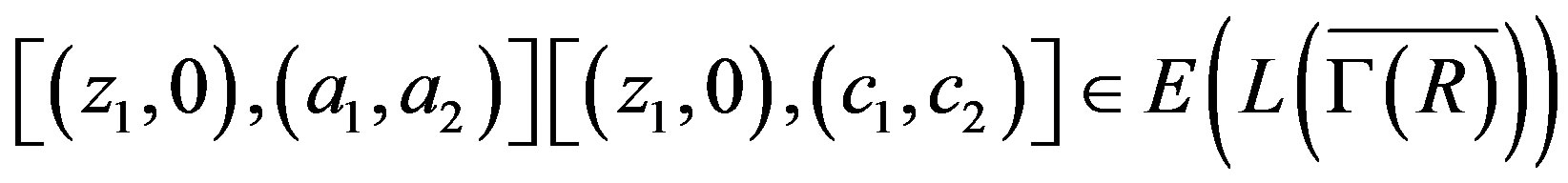 .
.
And 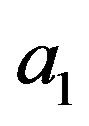 or
or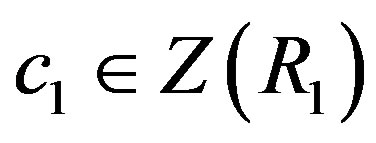 , say
, say 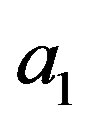 implies that
implies that
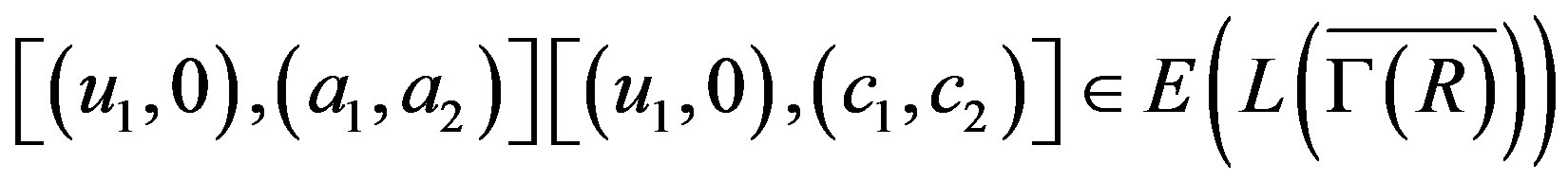
where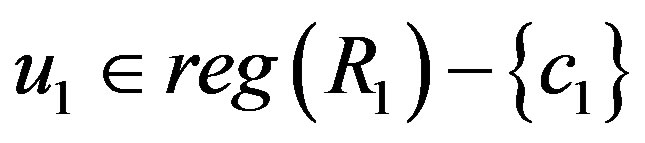 .
.
Case II: 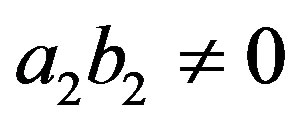 and
and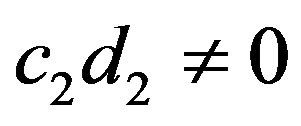 . Then there exists
. Then there exists 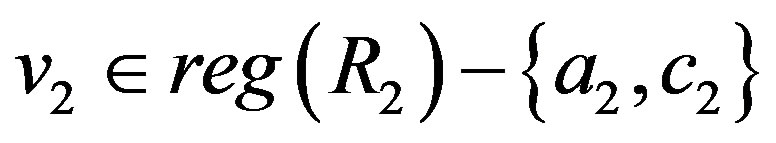 and hence
and hence
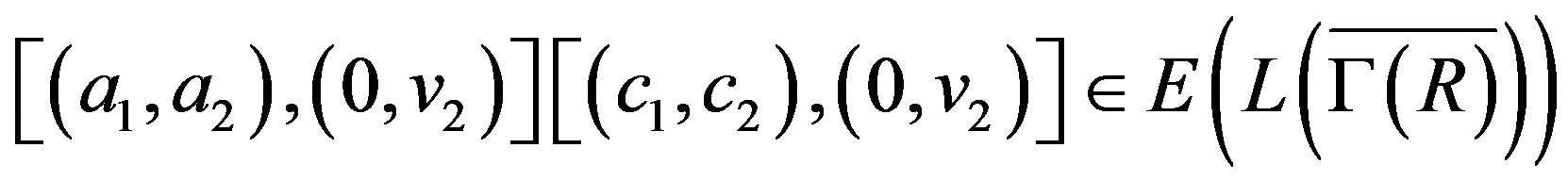 .
.
Case III: 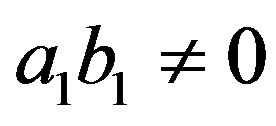 and
and 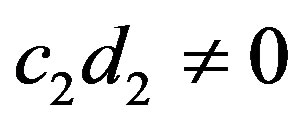 or
or 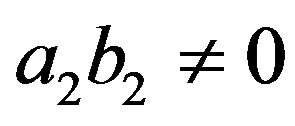 and
and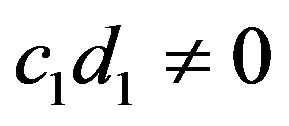 . Let
. Let 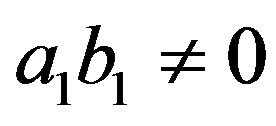 and
and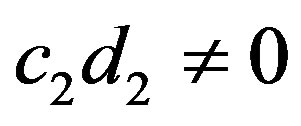 . Then
. Then
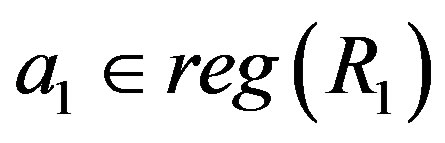 implies that
implies that
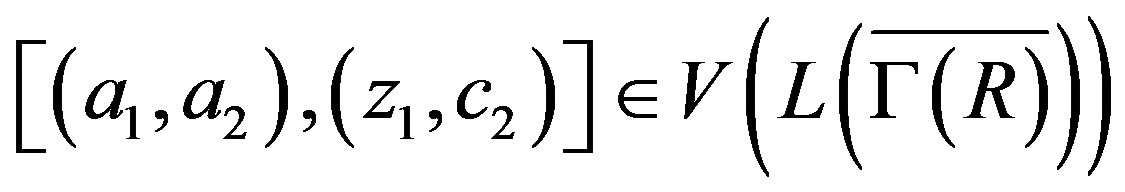 and
and
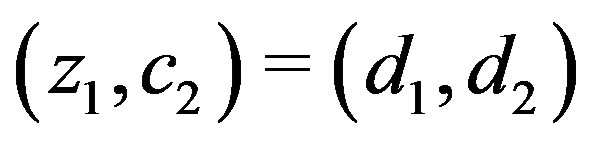 or
or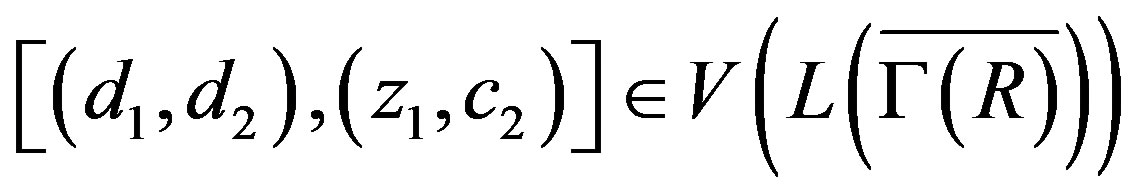 .
.
And if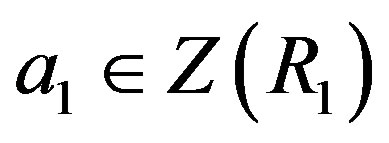 , then
, then 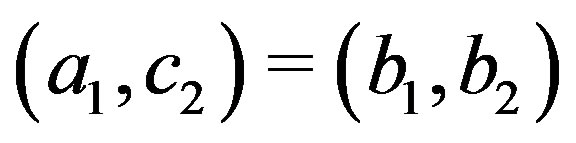 or
or
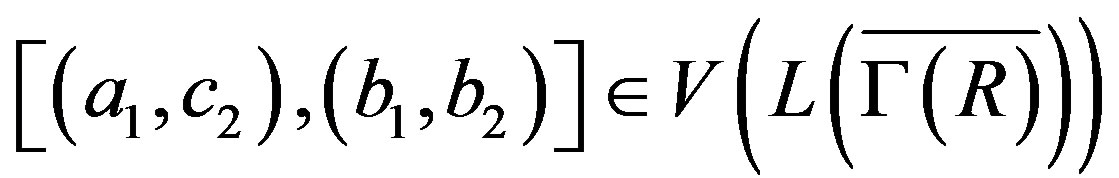 and
and 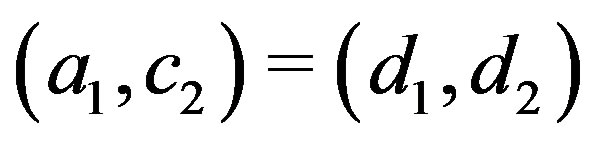 or
or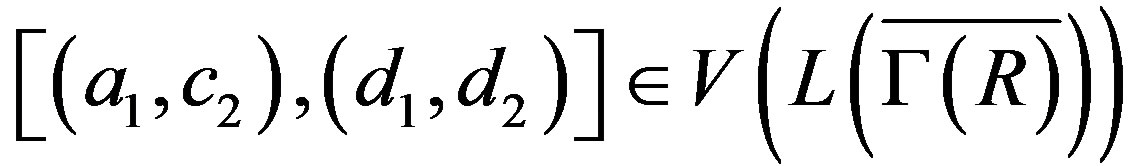 .
. 
For ,
, 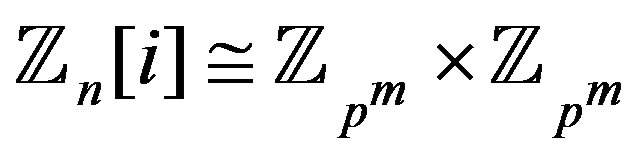 [7] and for
[7] and for
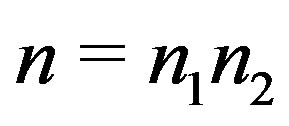 with
with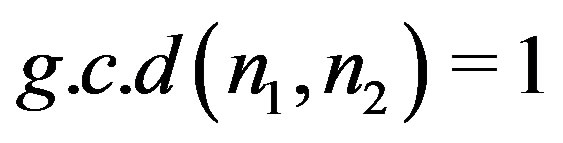 ,
,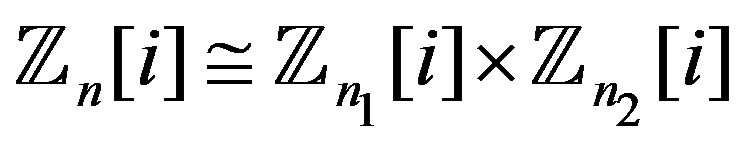 .
.
Moreover 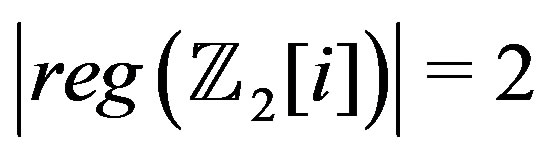 and
and 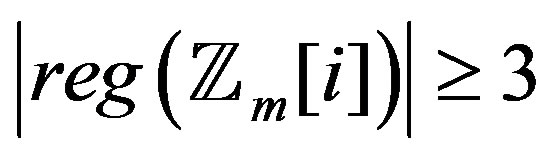 for
for
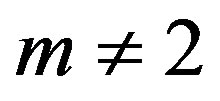 . An immediate consequence of Theorem 3.3 is the following.
. An immediate consequence of Theorem 3.3 is the following.
Theorem 3.4 Let 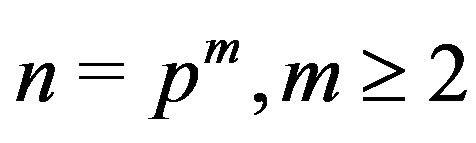 or n is a composite such that
or n is a composite such that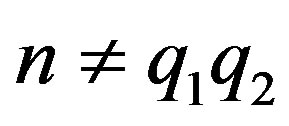 . Then
. Then
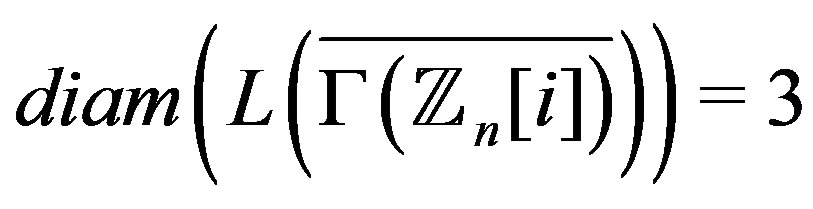 .
.
4. The Radius and the Girth of the Graph 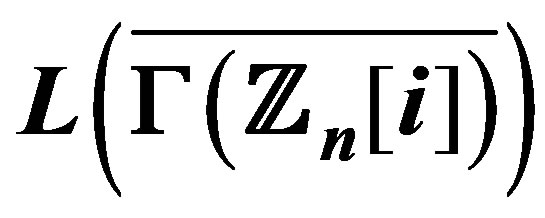
For a connected graph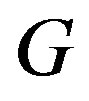 , the radius of
, the radius of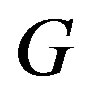 ,
, 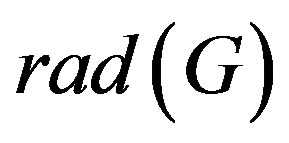 , is the minimum eccentricity among the vertices of
, is the minimum eccentricity among the vertices of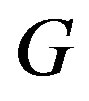 . So,
. So,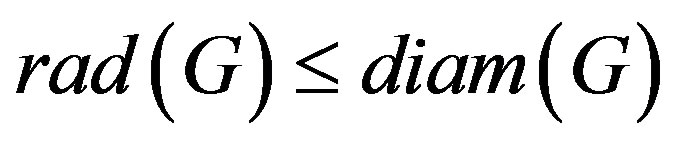 . Since for any
. Since for any
 ,
, 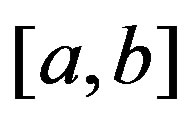 and
and 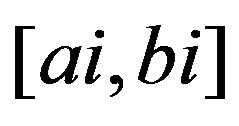 are non adjacent,
are non adjacent, . Using Theorem 3.2 gives for
. Using Theorem 3.2 gives for  or
or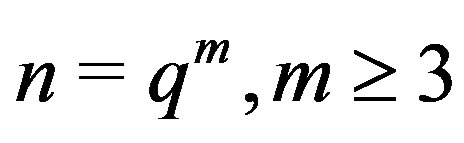 ,
,
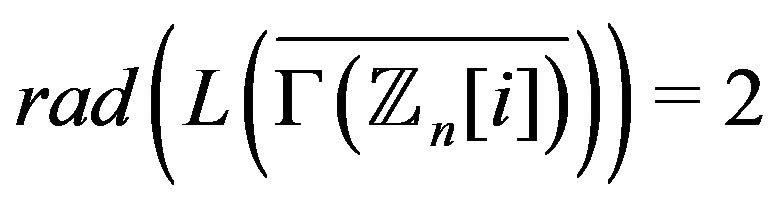 .
.
Theorem 4.1 If 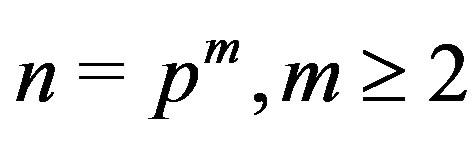 or
or 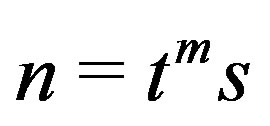 where
where
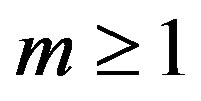 ,
, 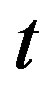 is prime integer,
is prime integer, 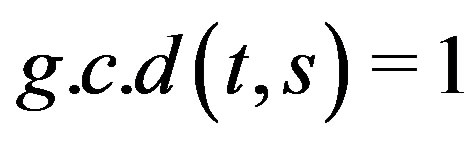 and
and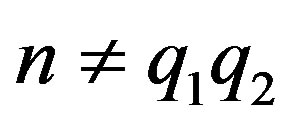 then
then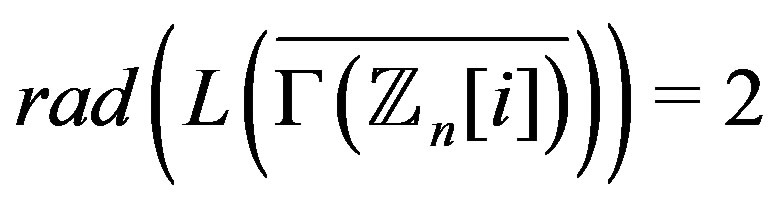 .
.
Proof. Since 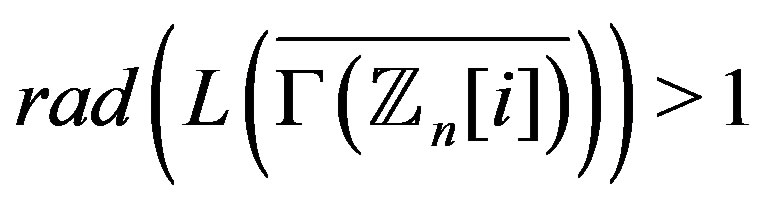 to show that
to show that
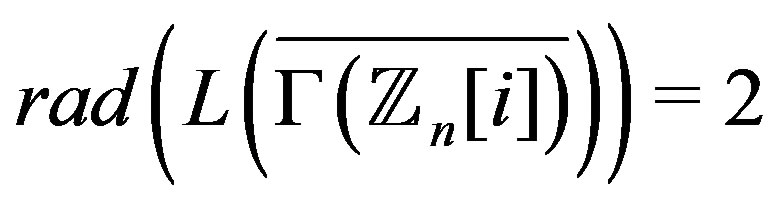 it is enough to find a vertex
it is enough to find a vertex
 with eccentricity 2. If
with eccentricity 2. If
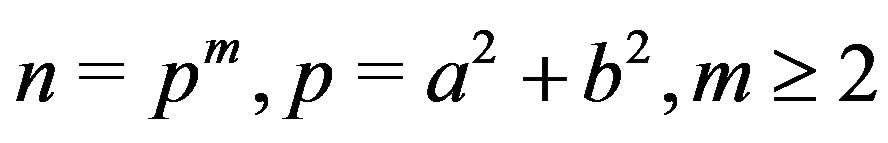 , then
, then
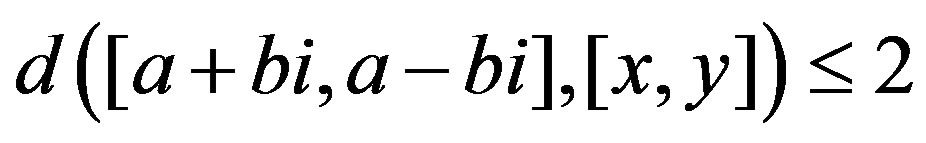 for every
for every
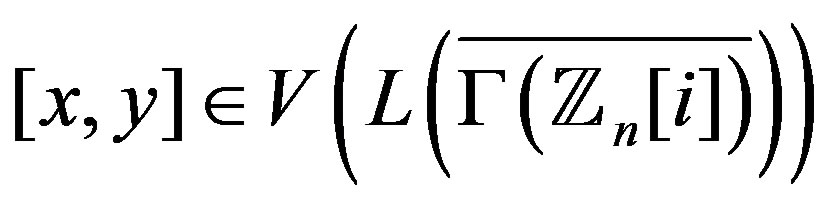 . So
. So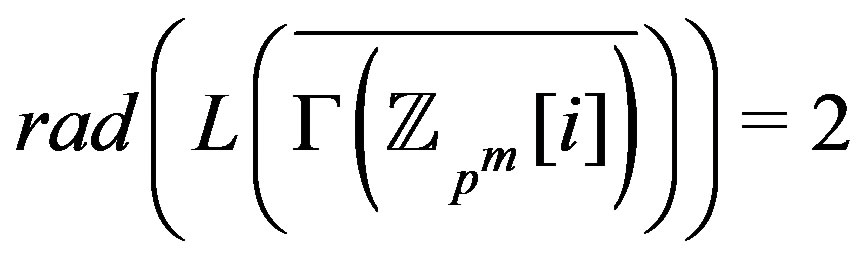 .
.
Now, assume that 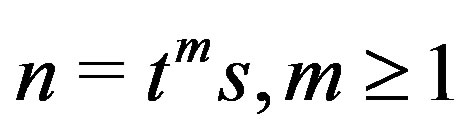 and
and
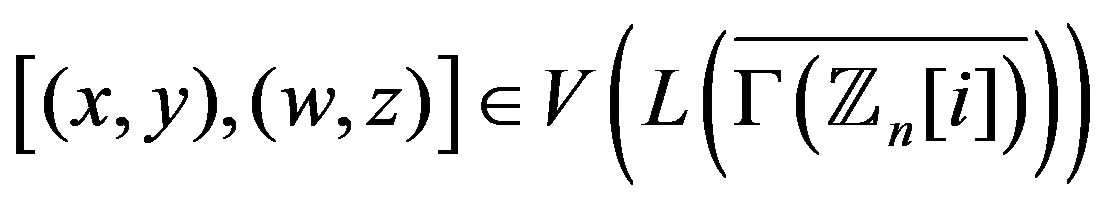 .
.
Then we have four cases:
Case I: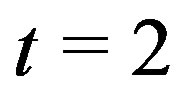 . Then
. Then
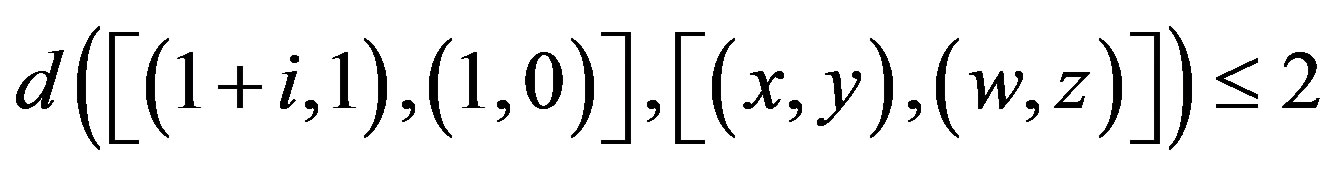 .
.
Case II: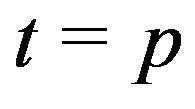 . Then
. Then
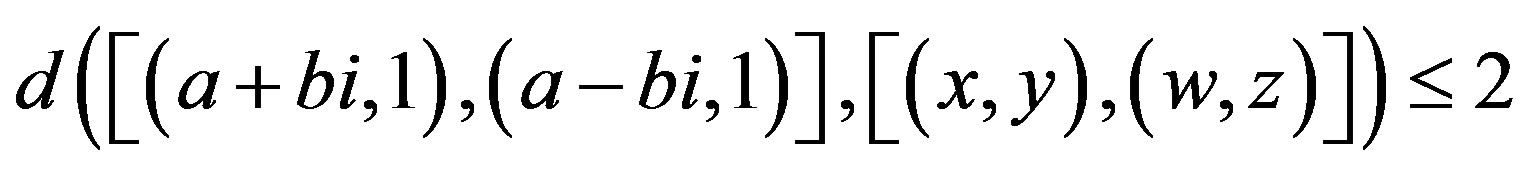 .
.
Case III: 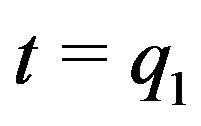 and
and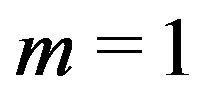 . Then
. Then  and hence there exists
and hence there exists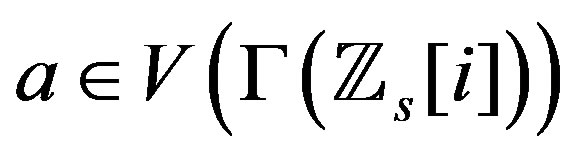 . So,
. So,
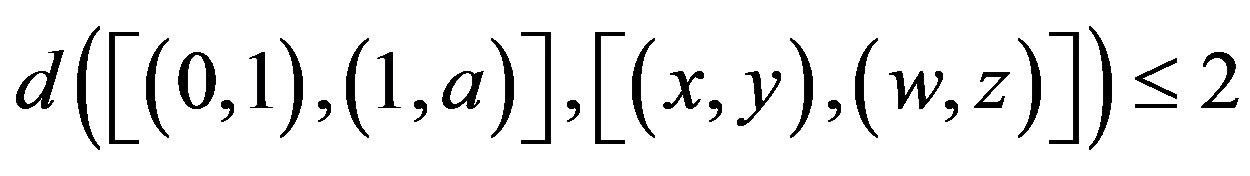 .
.
Case IV: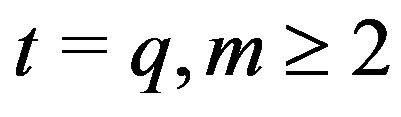 . Then
. Then
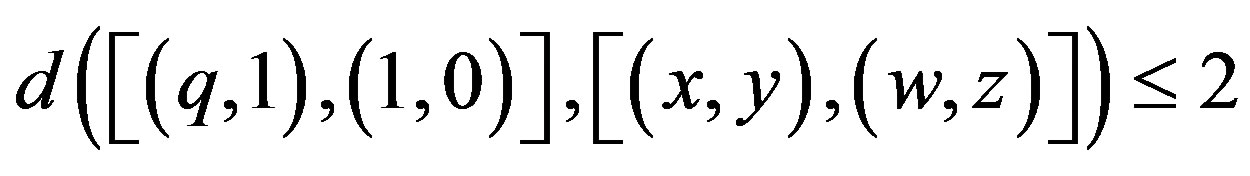 .
. 
Theorem 4.2 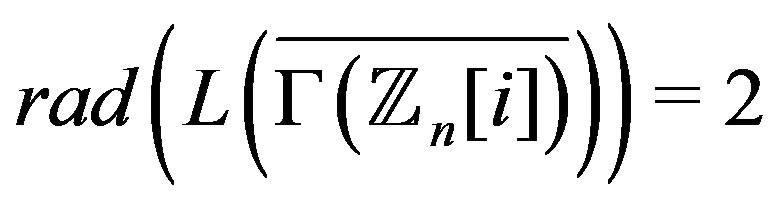 if and only if
if and only if
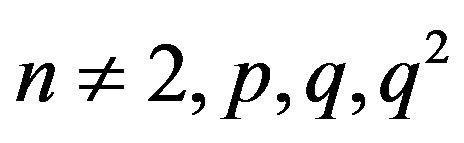 or
or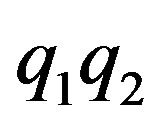 .
.
Vising [8], proved that for a connected simple graph 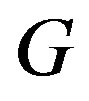 with n-vertices and radius 2, the upper bound of the number of edges of
with n-vertices and radius 2, the upper bound of the number of edges of 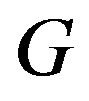 is
is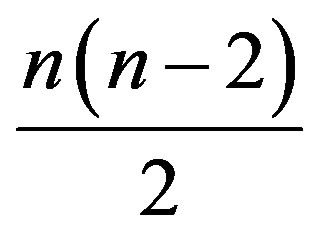 . Then Golberg [9]
. Then Golberg [9]
proved that the lower bound of numbers of edges of a simple connected graph 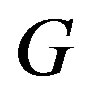 with radius 2 is
with radius 2 is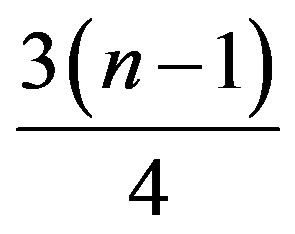 .
.
So we can conclude the following.
Theorem 4.3 For 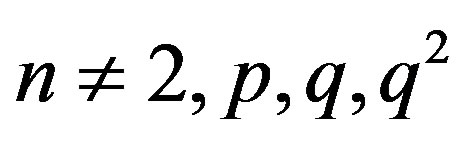 or
or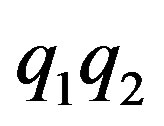 ,
,
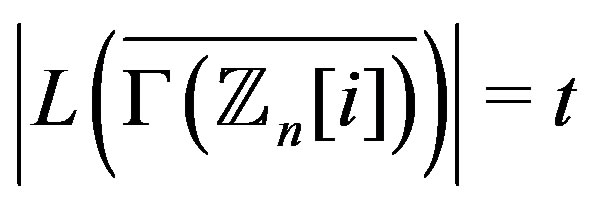 implies that
implies that
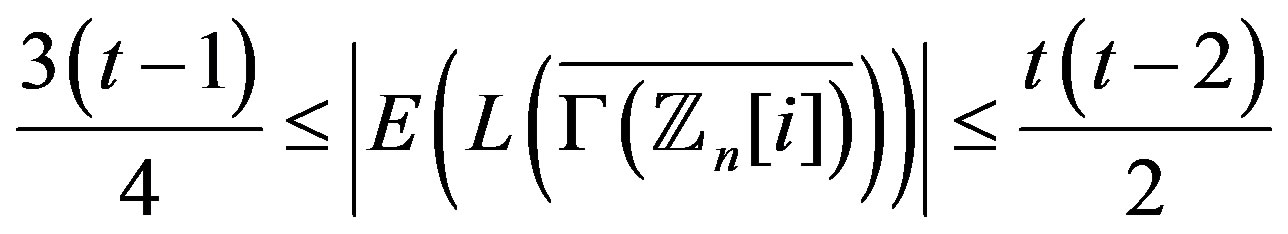 .
.
The girth of a graph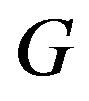 ,
, 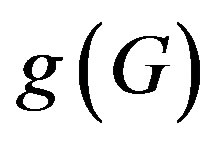 is the length of a shortest cycle contained in the graph. If the graph does not contain any cycles (i.e.. it’s an acyclic graph), its girth is defined to be infinity. If
is the length of a shortest cycle contained in the graph. If the graph does not contain any cycles (i.e.. it’s an acyclic graph), its girth is defined to be infinity. If 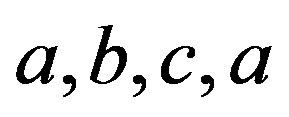 is a cycle of length three in
is a cycle of length three in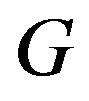 . Then
. Then 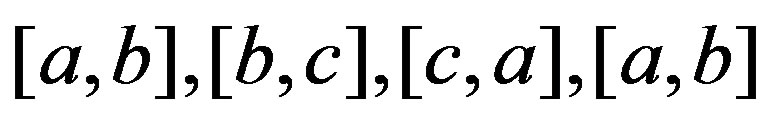 is a cycle of length 3 in
is a cycle of length 3 in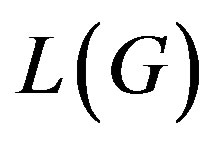 . So,
. So, 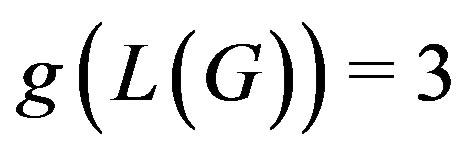 whenever
whenever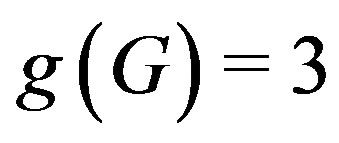 . In [3] it is proved that the girth of
. In [3] it is proved that the girth of
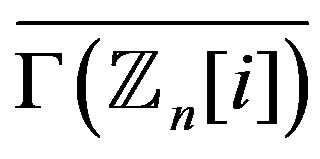 equals 3 for
equals 3 for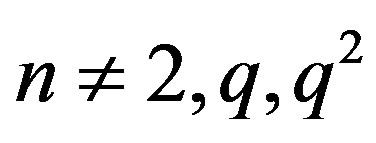 . So, we have the following.
. So, we have the following.
Theorem 4.4 For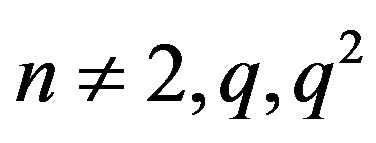 ,
,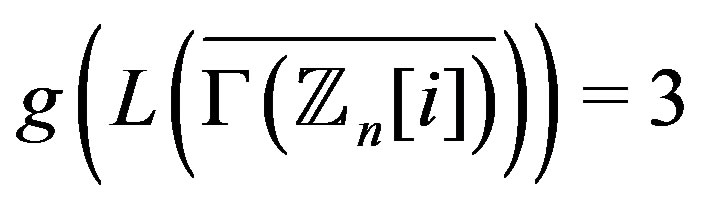 .
.
5. The Locally Connected Property of the Graphs  and
and 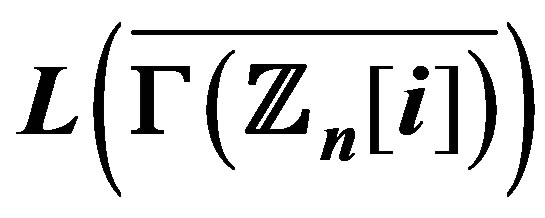
We say that a vertex 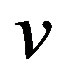 is locally connected if the neighborhood of
is locally connected if the neighborhood of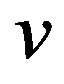 ,
,  , is connected; and
, is connected; and 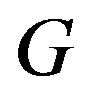 is locally connected if every vertex of
is locally connected if every vertex of 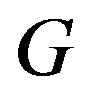 is locally connected.
is locally connected.
Theorem 5.1 If 
 for
for 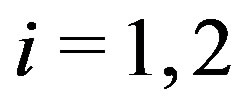 and either
and either 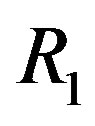 or
or 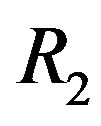 is not ID, then
is not ID, then 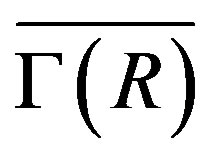 is locally connected.
is locally connected.
Proof. Suppose that 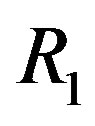 is not ID and
is not ID and
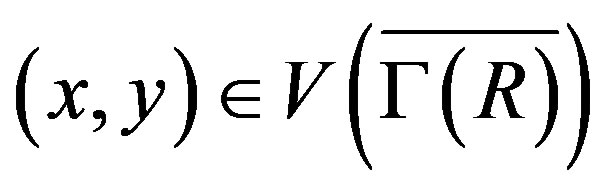 . Then we have two cases:
. Then we have two cases:
Case I: 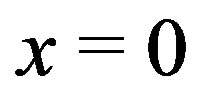 or
or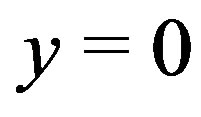 . If
. If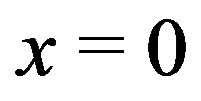 , then there exists
, then there exists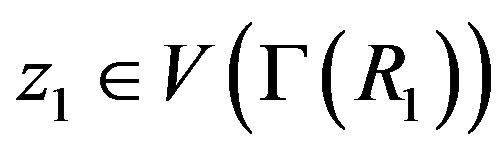 . So
. So 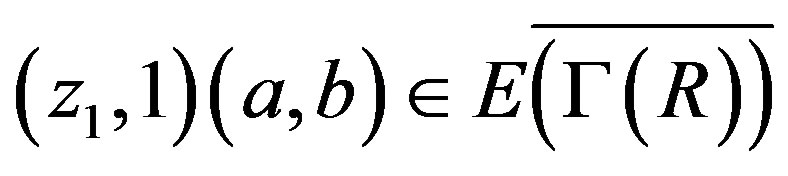 for all
for all
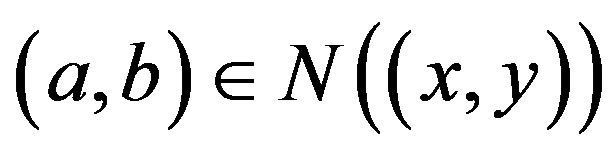 . And if
. And if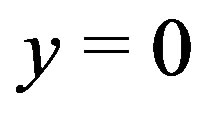 , then there exists
, then there exists
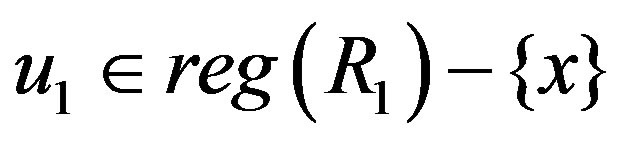 such that
such that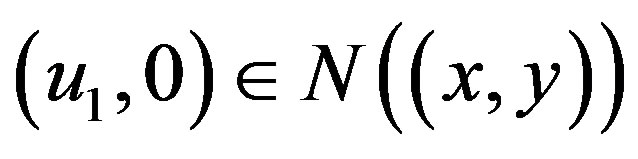 . Therefore,
. Therefore, 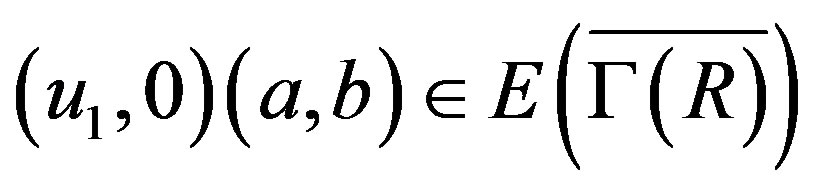 for every
for every
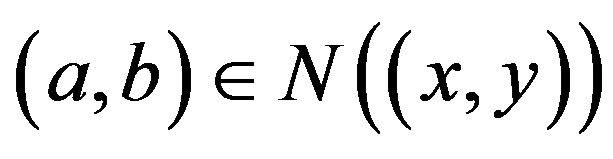 . So
. So 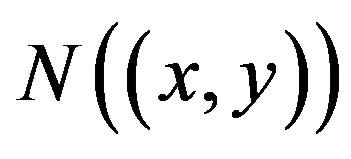 is connected.
is connected.
Case II:  and
and . Then there exist
. Then there exist
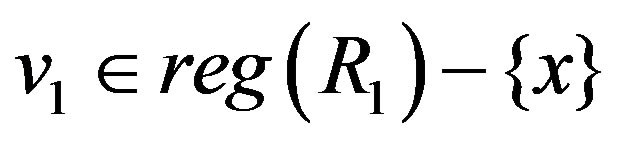 ,
, 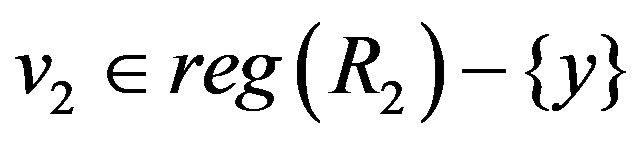 and
and
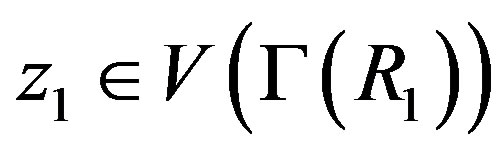 such that
such that 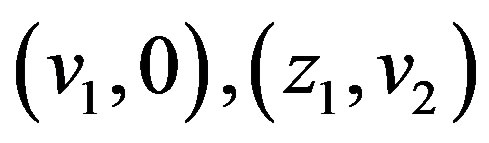 and
and
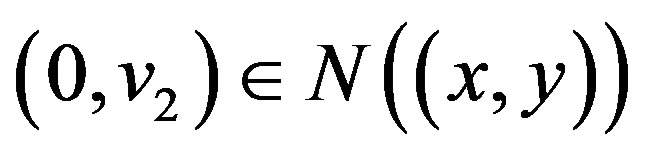 . Moreover,
. Moreover,
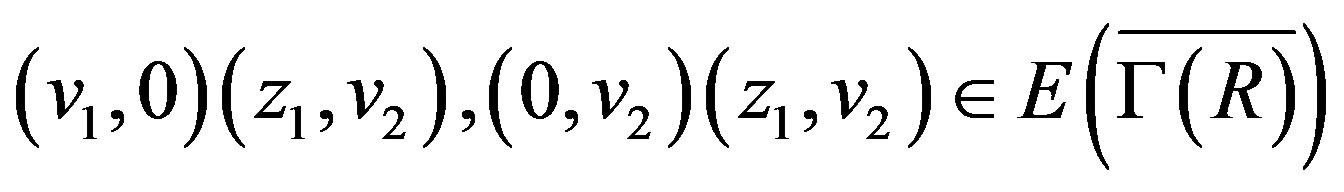 . And for every
. And for every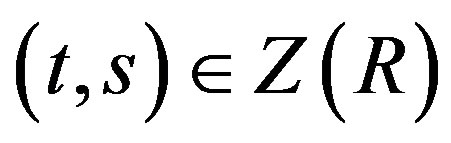 ,
, 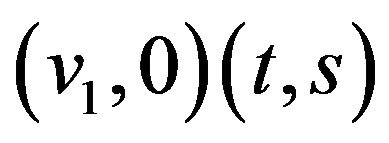 or
or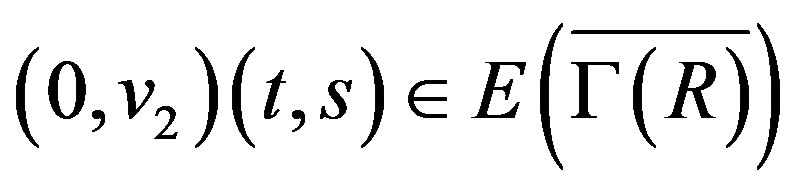 . So
. So 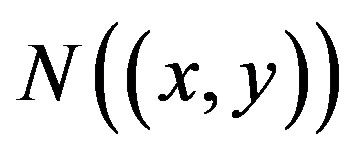 is connected.
is connected. 
Theorem 5.2 If 
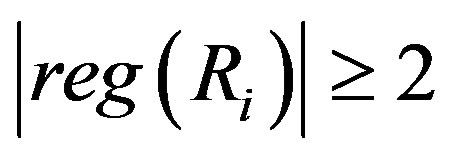 for
for
 and either
and either 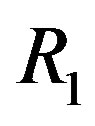 or
or 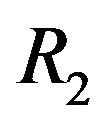 is not ID, then
is not ID, then 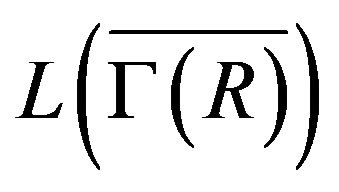 is locally connected.
is locally connected.
Proof. Suppose that 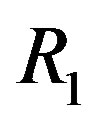 is not ID,
is not ID, 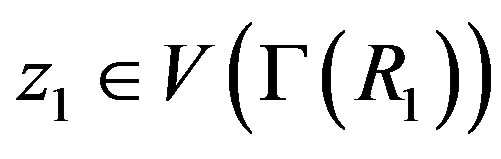
and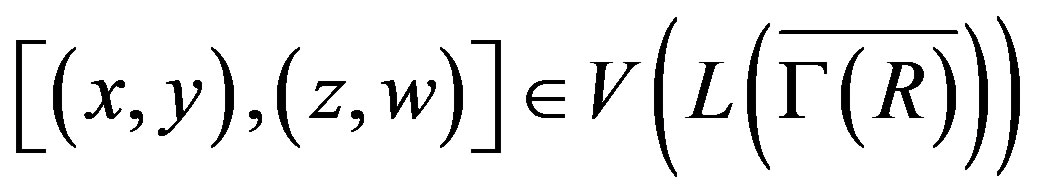 , then we have three cases:
, then we have three cases:
Case I: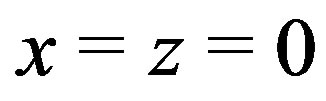 . Then
. Then
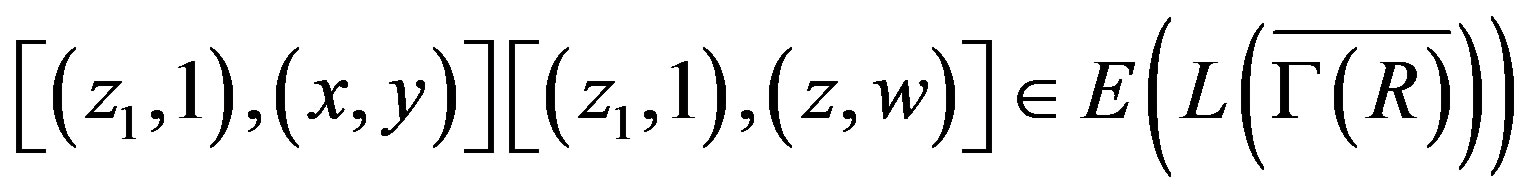 .
.
Case II: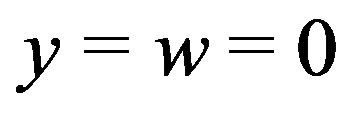 . If
. If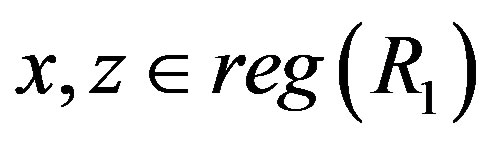 , then
, then
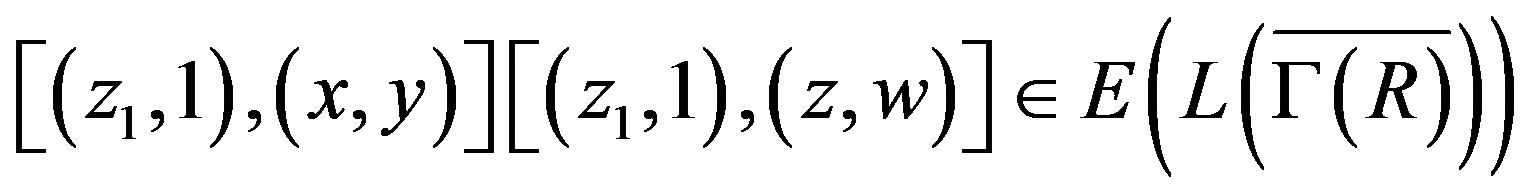 .
.
Otherwise there exists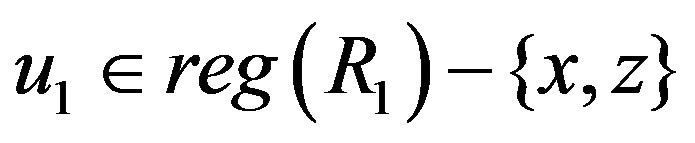 . So,
. So,
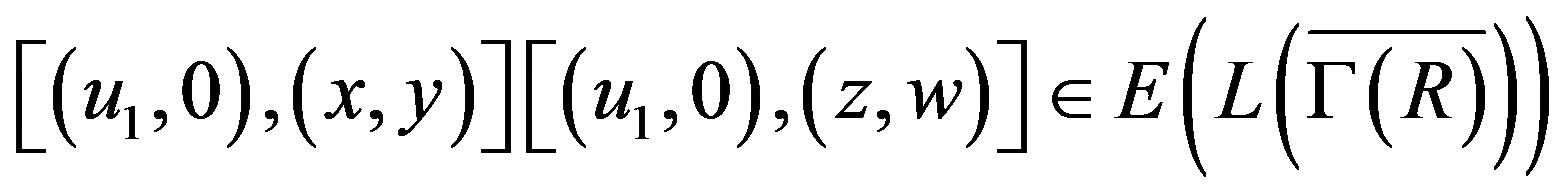 .
.
Case III: 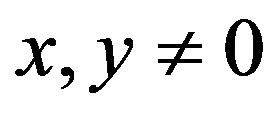 or
or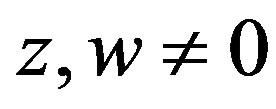 . Assume that
. Assume that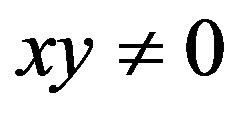 , then
, then 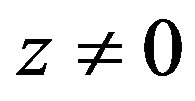 implies that there exists
implies that there exists 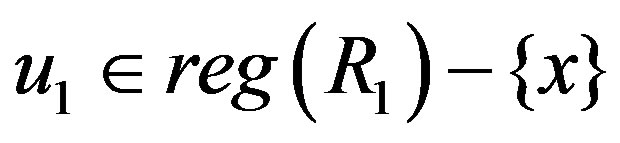 satisfies
satisfies
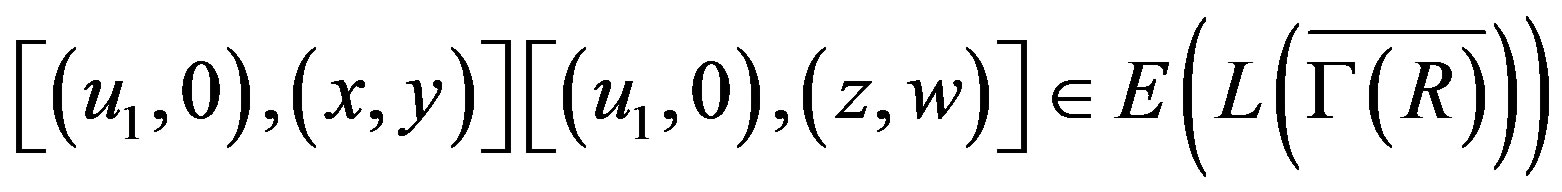 .
.
While 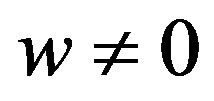 implies that that there exists
implies that that there exists
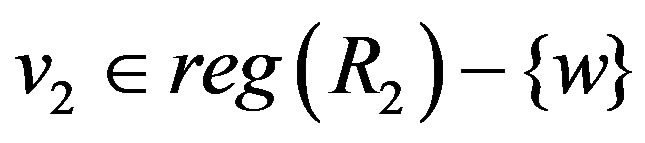 satisfies
satisfies
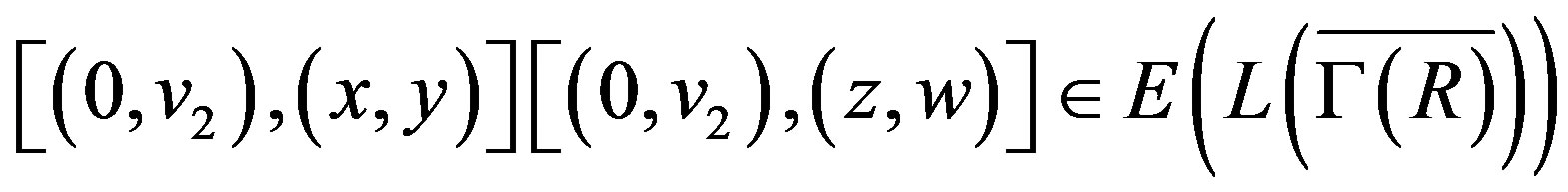 .
. 
From Theorem 5.1 and Theorem 5.2 we conclude the following.
Theorem 5.3 If 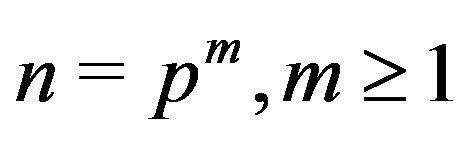 or
or 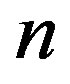 is a composite integer such that
is a composite integer such that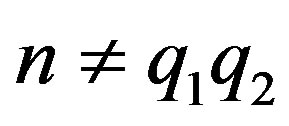 , then both
, then both 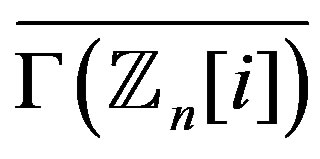 and
and
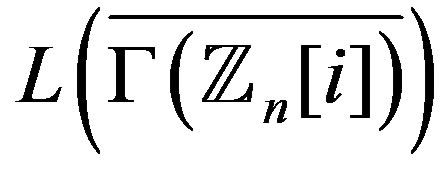 are locally connected.
are locally connected.
6. When Is 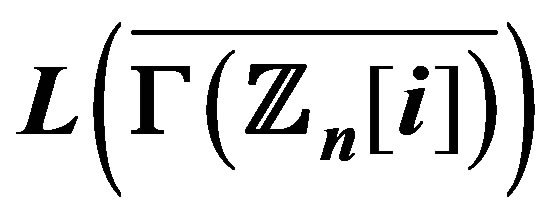 Hamiltonian?
Hamiltonian?
A Hamiltonian cycle is a cycle that visits each vertex exactly once (except the vertex which is both the start and end, and so is visited twice). A graph that contains a Hamiltonian cycle is called a Hamiltonian graph. The line graph of a graph 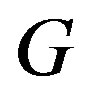 with more than 4 vertices and diameter 2 is Hamiltonian [10]. But
with more than 4 vertices and diameter 2 is Hamiltonian [10]. But 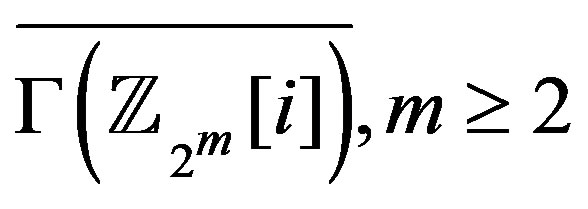 is disconnected with one isolated vertex
is disconnected with one isolated vertex 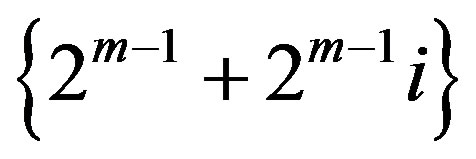 and the other component, call this component
and the other component, call this component , with diameter 2 [3]. So,
, with diameter 2 [3]. So,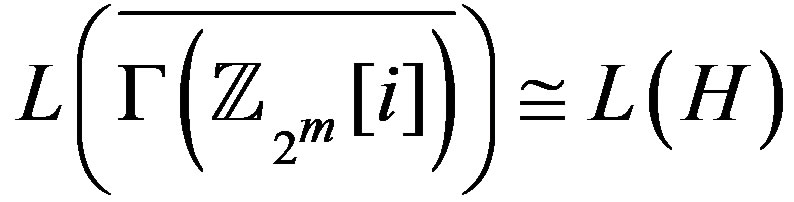 . Similarly,
. Similarly,
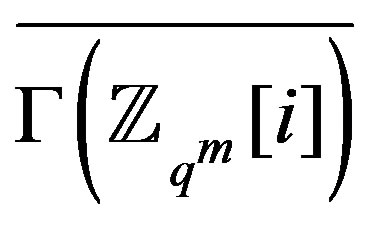 has a connected subgraph
has a connected subgraph  with diameter 2 and
with diameter 2 and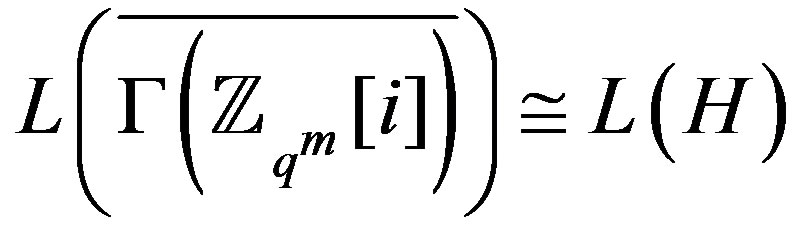 . Hence, the following result is obtained.
. Hence, the following result is obtained.
Theorem 6.1 If 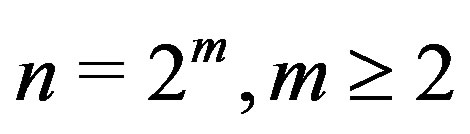 or
or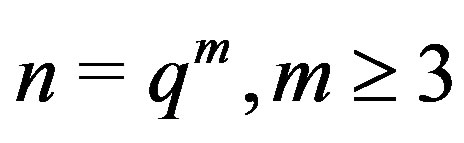 , then
, then
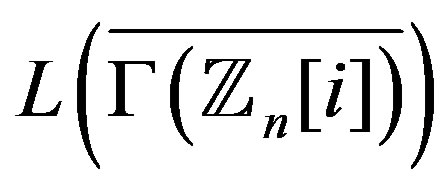 is Hamiltonian.
is Hamiltonian.
Oberly and Sumner [11] proved that every connected, locally connected claw free graph (i.e. it does not contain a complete bipartite graph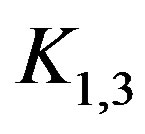 ) is hamiltonian. Since the line graph is claw free, using Theorem 5.3, we get the following.
) is hamiltonian. Since the line graph is claw free, using Theorem 5.3, we get the following.
Theorem 6.2 If 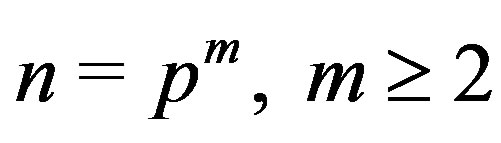 or
or 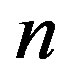 is a composite integer such that
is a composite integer such that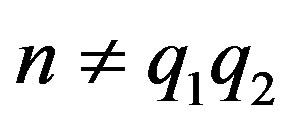 , then
, then 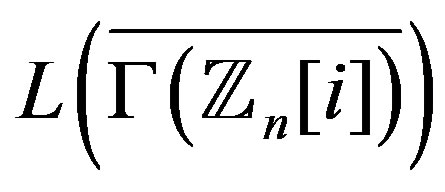 is hamiltonian.
is hamiltonian.
7. The Chromatic Number of the Graph 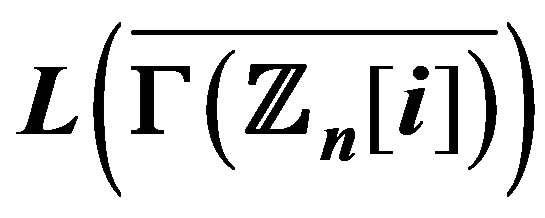
The edge coloring of a graph 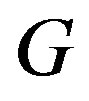 is an assignment of colors to the edges of the graph so that no two adjacent edges have the same color. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph denoted by
is an assignment of colors to the edges of the graph so that no two adjacent edges have the same color. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph denoted by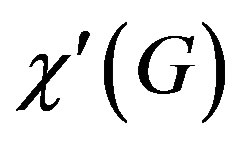 .
.
Lemma 7.1 [12]
If 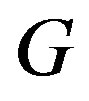 has order
has order 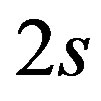 and
and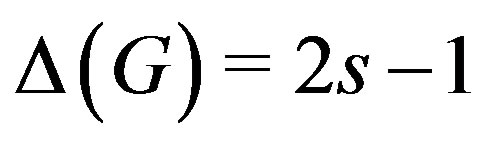 , then
, then 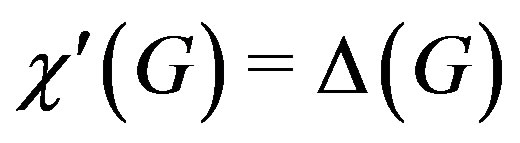 .
.
Theorem 7.2 If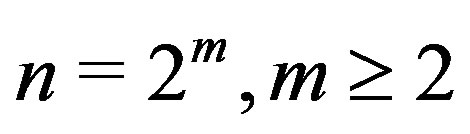 , then
, then
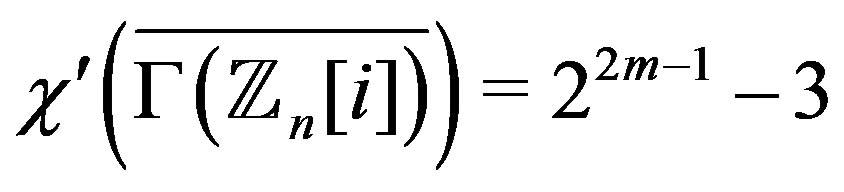 .
.
Proof. Note that in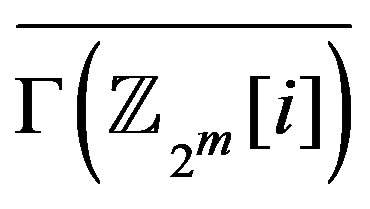 , the induced subgraph,
, the induced subgraph,
 , with
, with 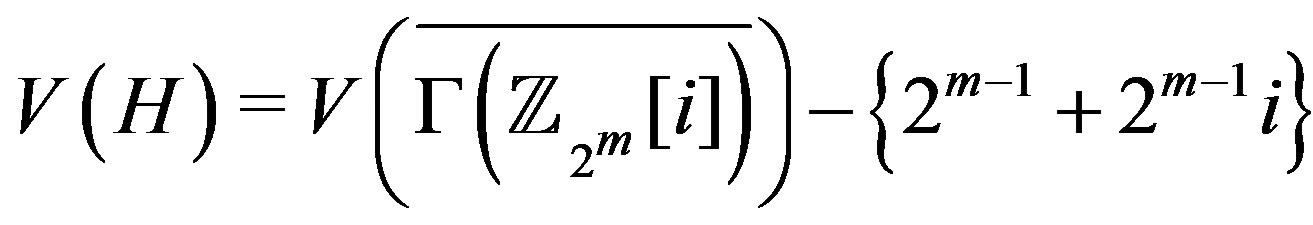 is connected,
is connected, 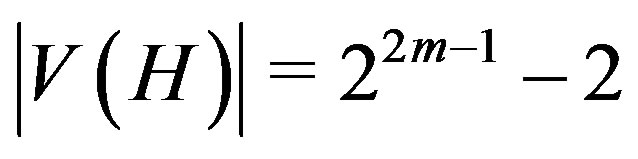 , [1] and
, [1] and
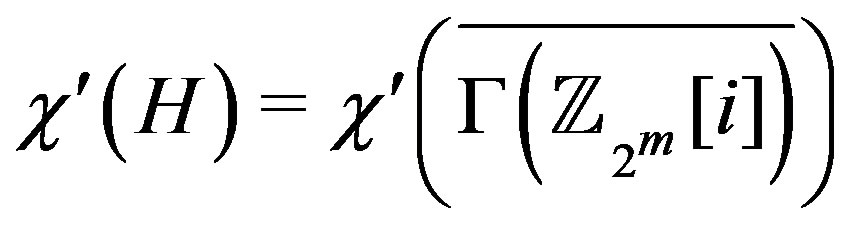 . Since the vertex
. Since the vertex 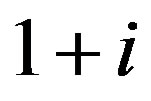 is adjacent to all other vertices in
is adjacent to all other vertices in , we have
, we have
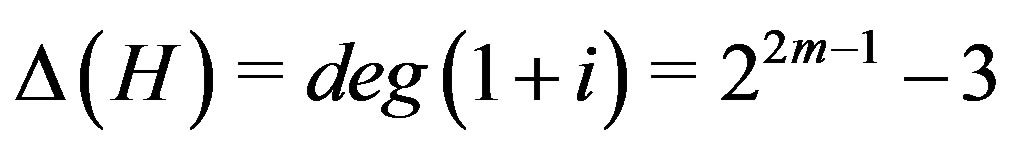 . Using Lemma 6.1,
. Using Lemma 6.1,
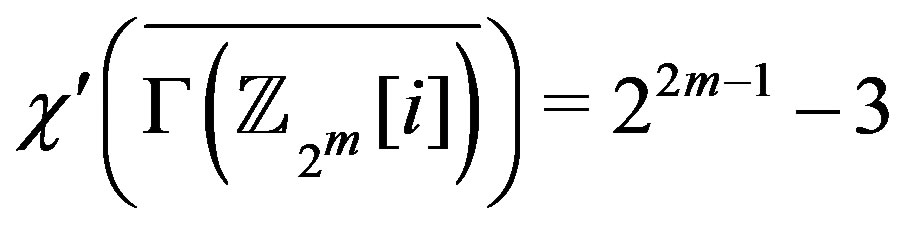 .
. 
Since 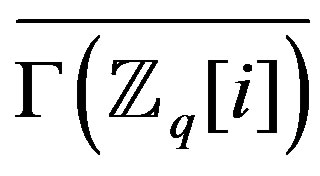 is empty graph and
is empty graph and
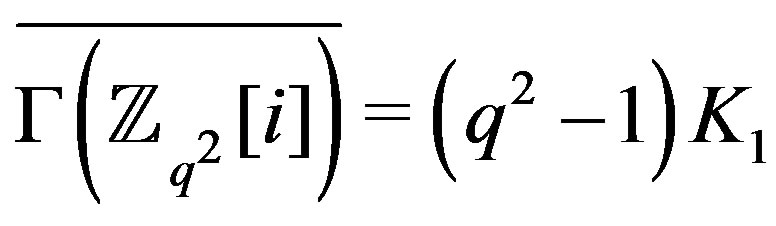 is edgeless with
is edgeless with 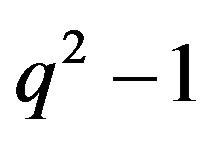 vertices, we consider the case
vertices, we consider the case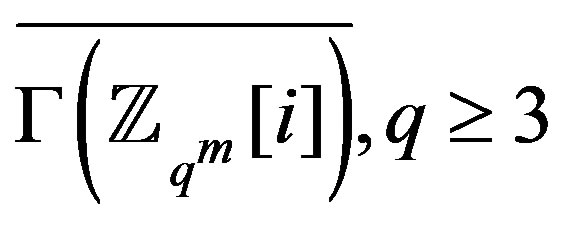 .
.
Theorem 7.3 If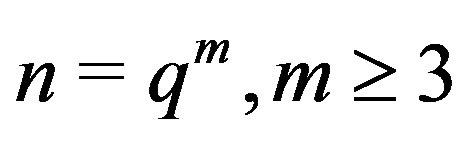 , then
, then
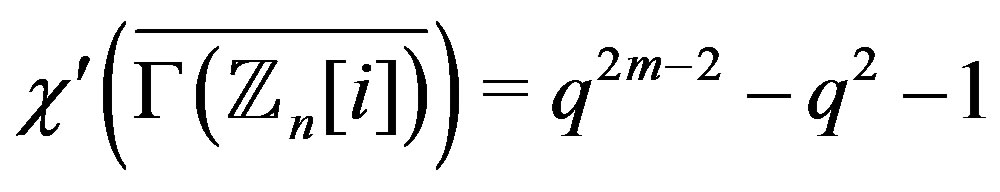
Proof. Let 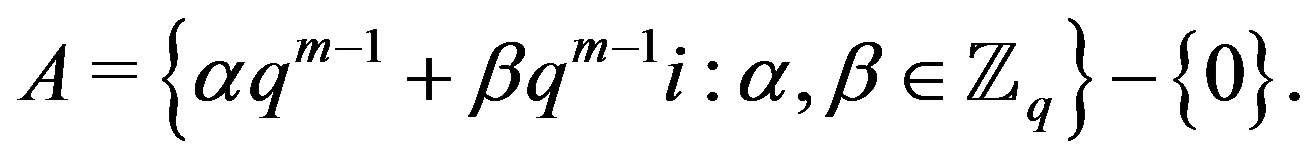
Then  is the set of all isolated vertices in
is the set of all isolated vertices in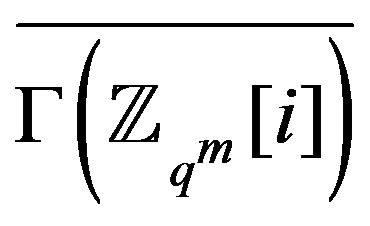 .
.
So the induced subgraph,  , with the vertices
, with the vertices
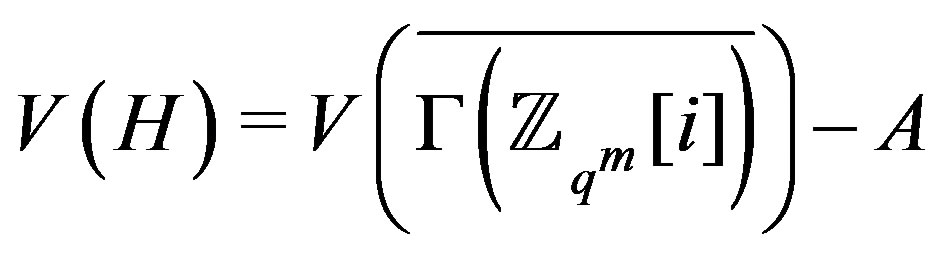 is a connected graph,
is a connected graph,
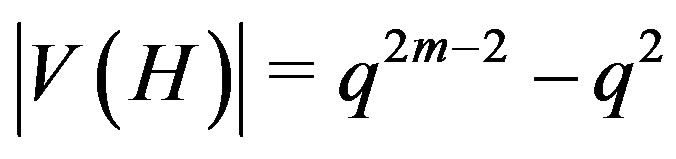 . Clearly the vertex
. Clearly the vertex 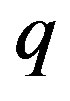 is adjacent to all other vertices in
is adjacent to all other vertices in  and hence,
and hence,
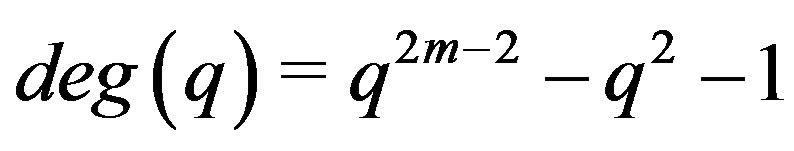 . Using Lemma 7.1,
. Using Lemma 7.1,

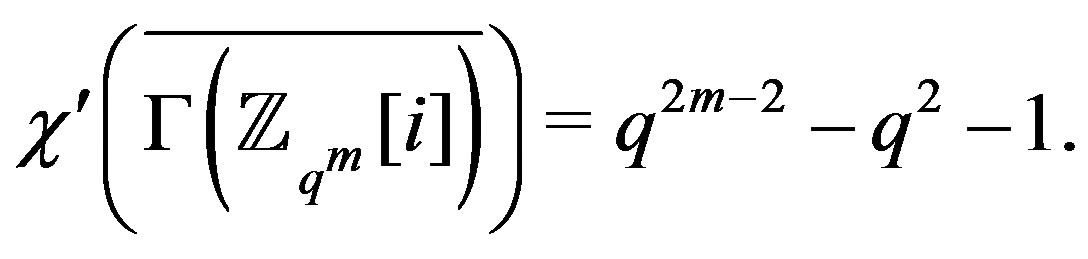
Finally we find the chromatic index of
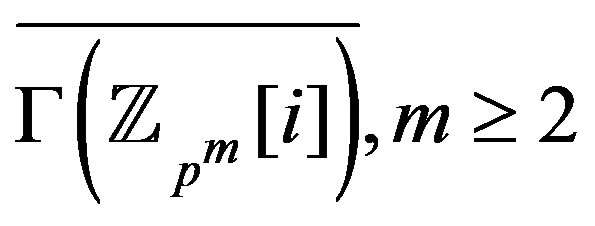 .
.
A subset  of the vertex set
of the vertex set 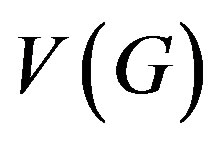 is said to be independent if no two vertices in this set are adjacent. A clique of a graph is a maximal complete subgraph. A graph
is said to be independent if no two vertices in this set are adjacent. A clique of a graph is a maximal complete subgraph. A graph 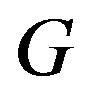 is said to be split if it’s vertex set can be partitioned into two subsets
is said to be split if it’s vertex set can be partitioned into two subsets  and
and 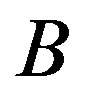 such that
such that  induces a clique and
induces a clique and 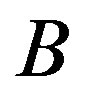 is independent in
is independent in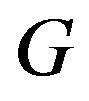 .
.
Lemma 7.4 [13] Let 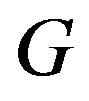 be a split graph. If
be a split graph. If 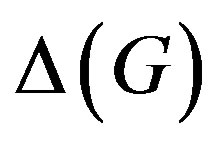 is odd, then
is odd, then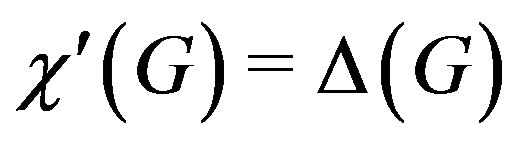 .
.
Theorem 7.5 If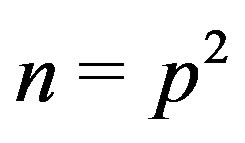 , then
, then
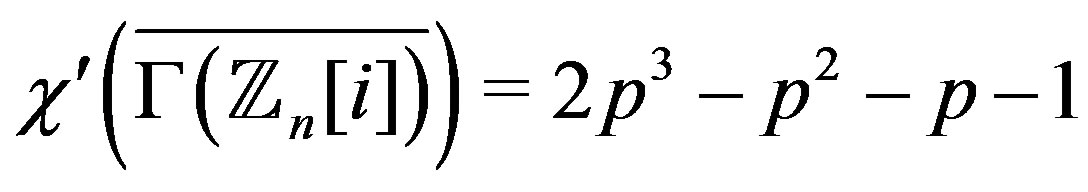 .
.
Proof. Since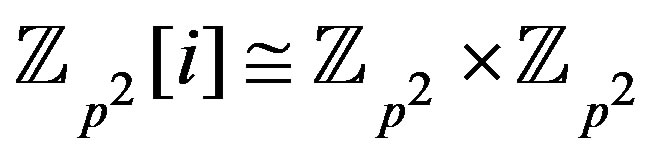 , it is enough to find
, it is enough to find
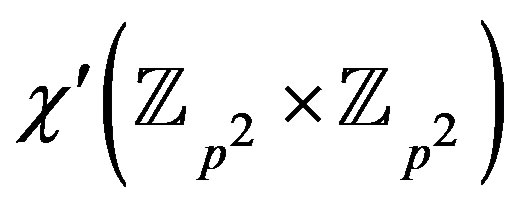 . First, we’ll show that
. First, we’ll show that 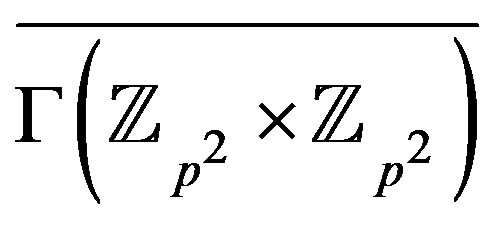 is a split graph. Let
is a split graph. Let
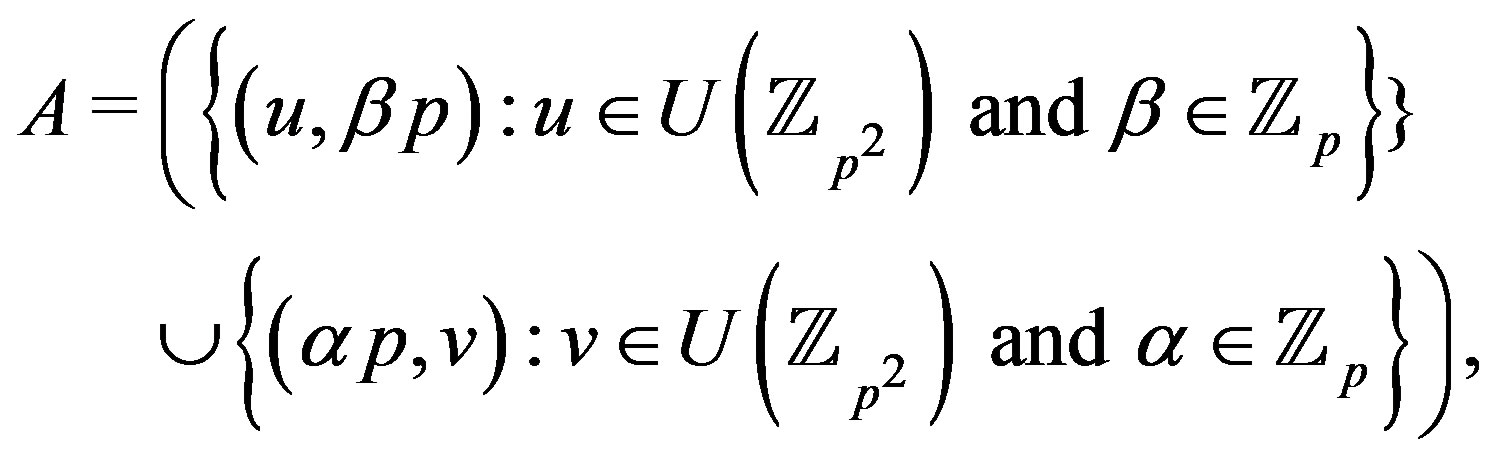
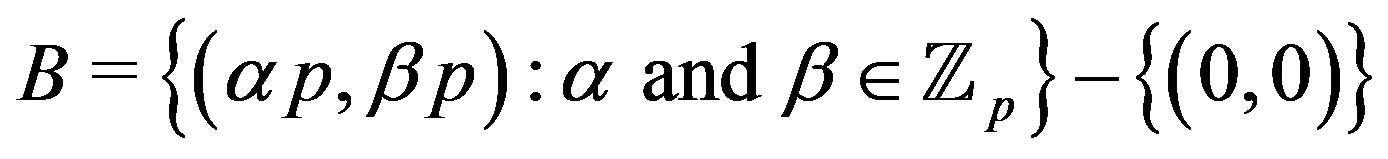 .
.
Clearly, 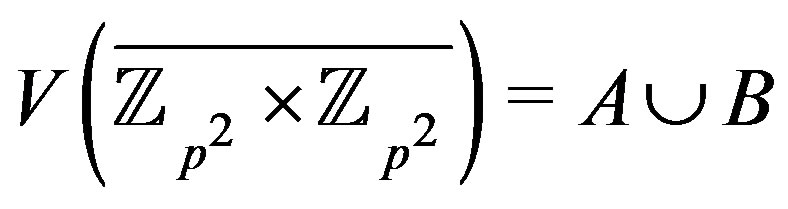 ,
,  induces a clique and
induces a clique and 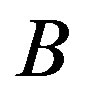 is independent. Therefore,
is independent. Therefore, 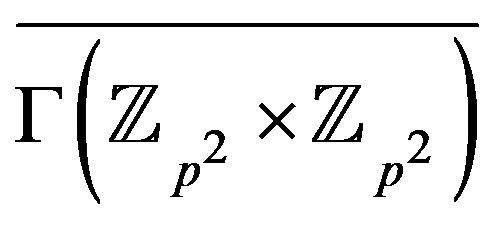 is a split graph. Moreover,
is a split graph. Moreover,
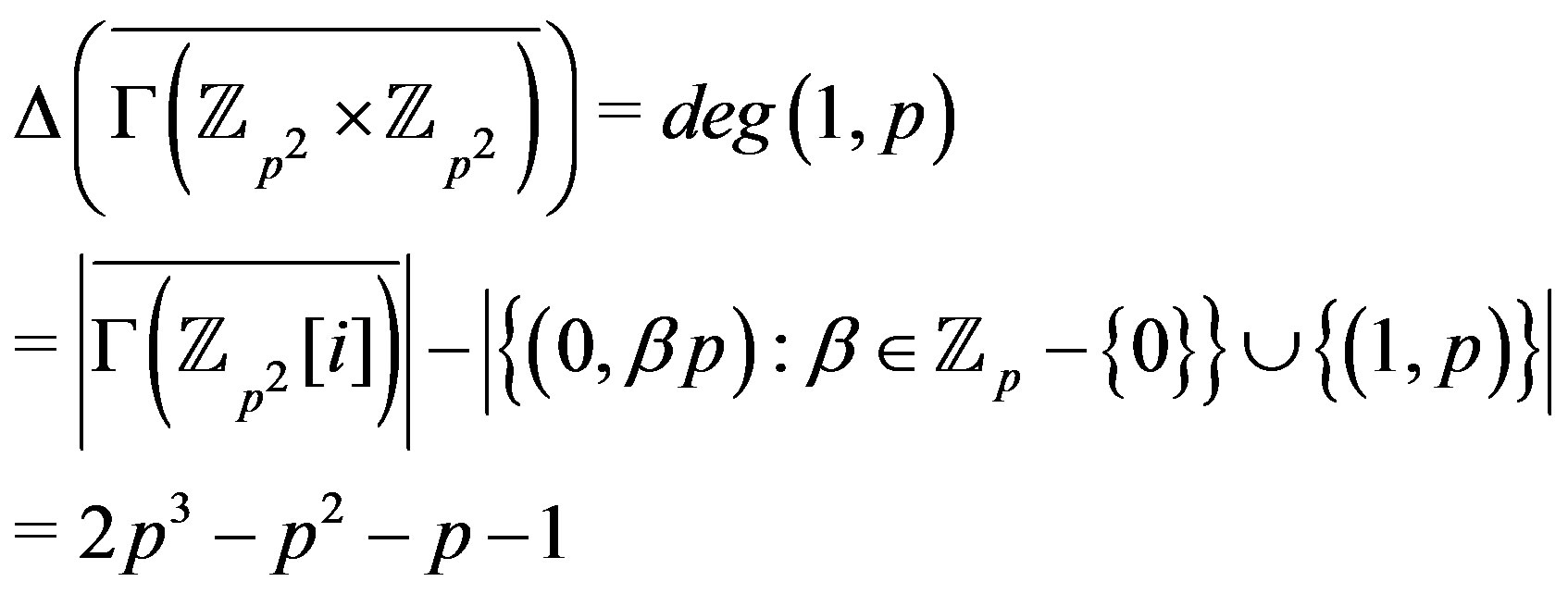
is odd. From Lemma 7.4,
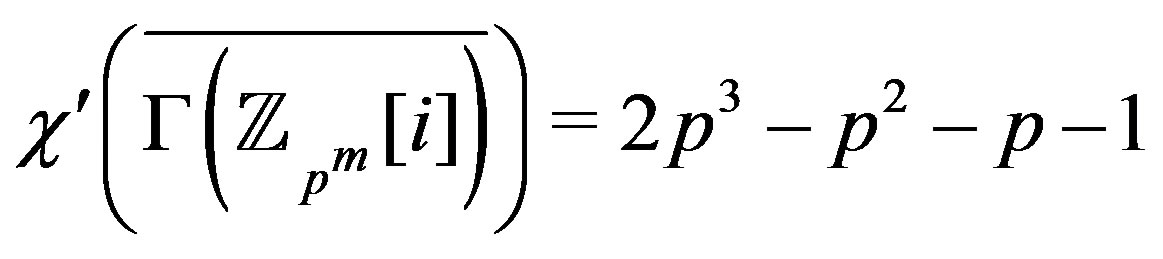 .
. 
A graph 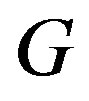 is said to be critical if
is said to be critical if 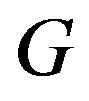 is connected and
is connected and 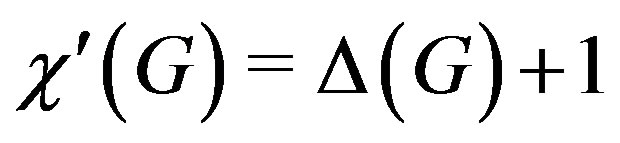 and for every edge
and for every edge  of
of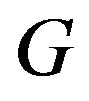 , we have
, we have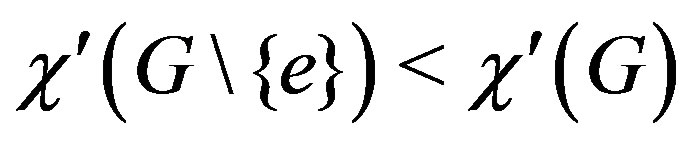 . The well-known Vizing’s theorem states that for a simple graph
. The well-known Vizing’s theorem states that for a simple graph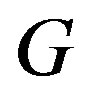 ,
, 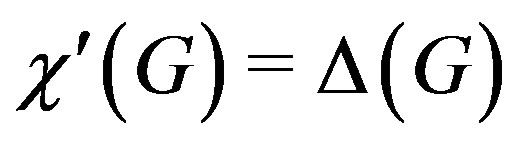 or
or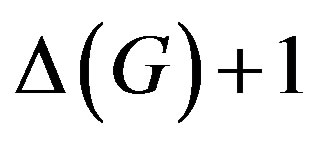 .
.
Lemma 7.6 [14]
If 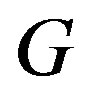 is a critical graph, then
is a critical graph, then 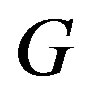 has at least
has at least 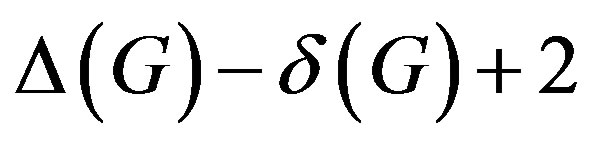 of vertices of maximum degree.
of vertices of maximum degree.
Therefore, if 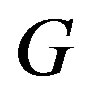 is a simple graph such that for every vertex
is a simple graph such that for every vertex 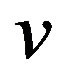 of maximum degree there exists an edge
of maximum degree there exists an edge 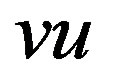 such that
such that 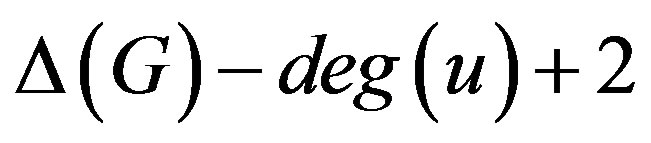 is more than the number of vertices with maximum degree in
is more than the number of vertices with maximum degree in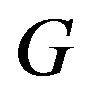 , we have
, we have 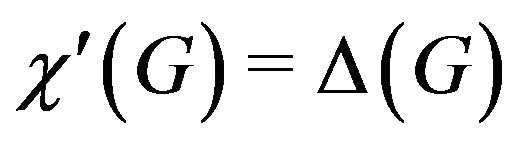 [13].
[13].
Theorem 7.7 If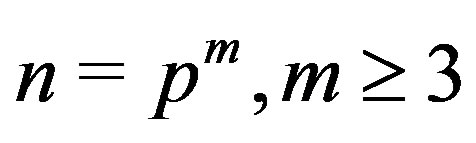 , then
, then
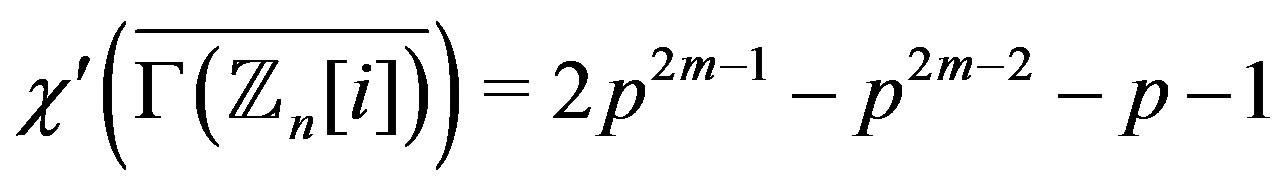 .
.
Proof. Let 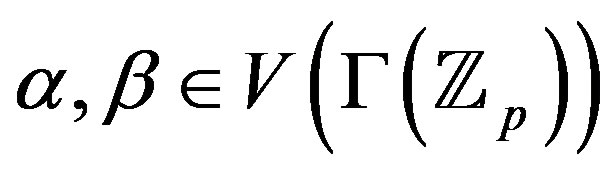 and
and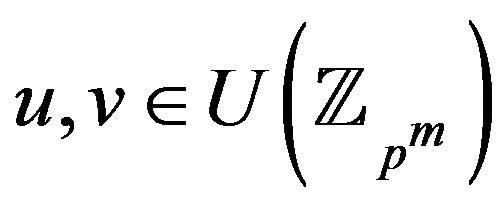 .
.
Then the vertices of 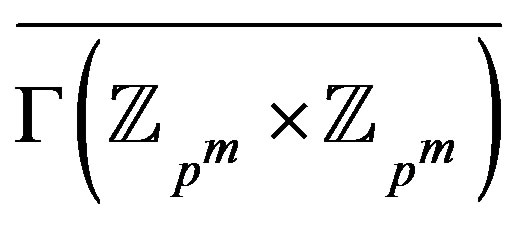 with maximum degree have the form
with maximum degree have the form 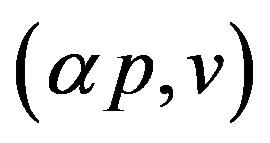 or
or 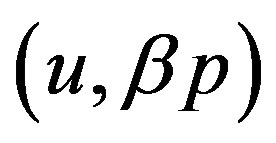 where
where 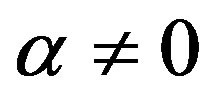 and
and 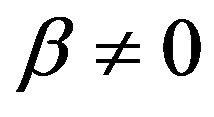 and
and
and
So,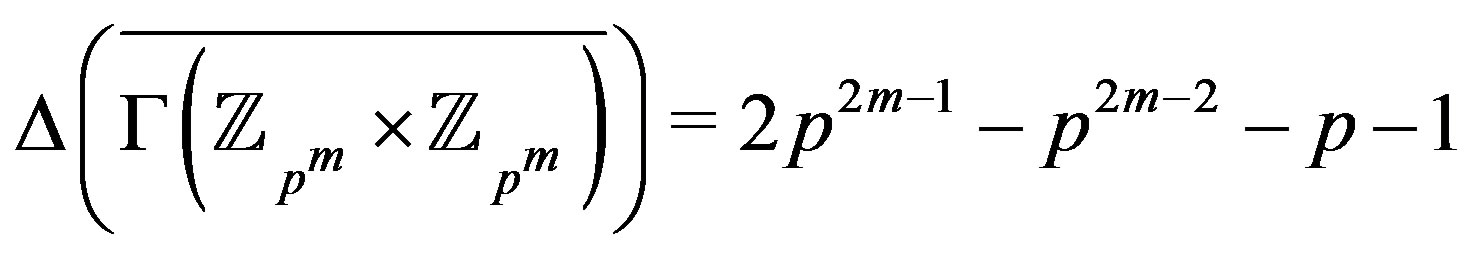 . And the vertices of
. And the vertices of 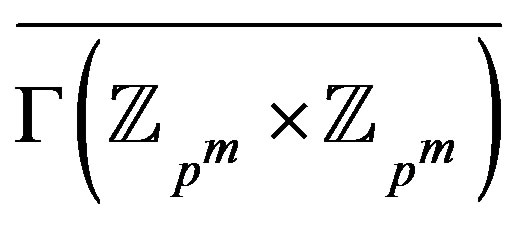 with minimum degree have the form
with minimum degree have the form 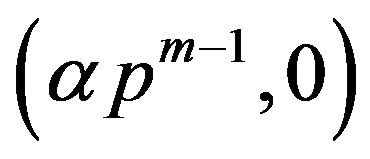 or
or 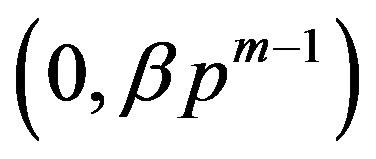 where
where
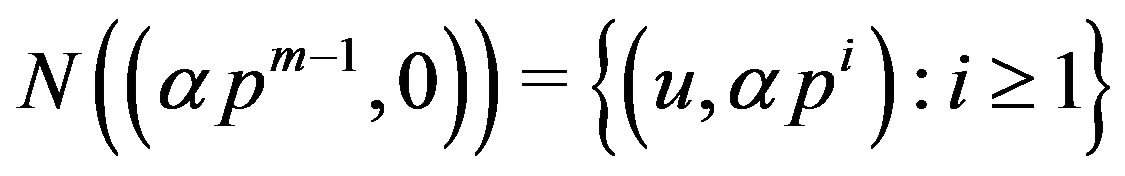 and
and
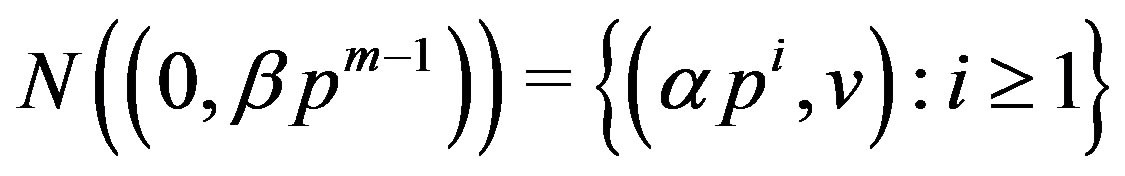 . So
. So
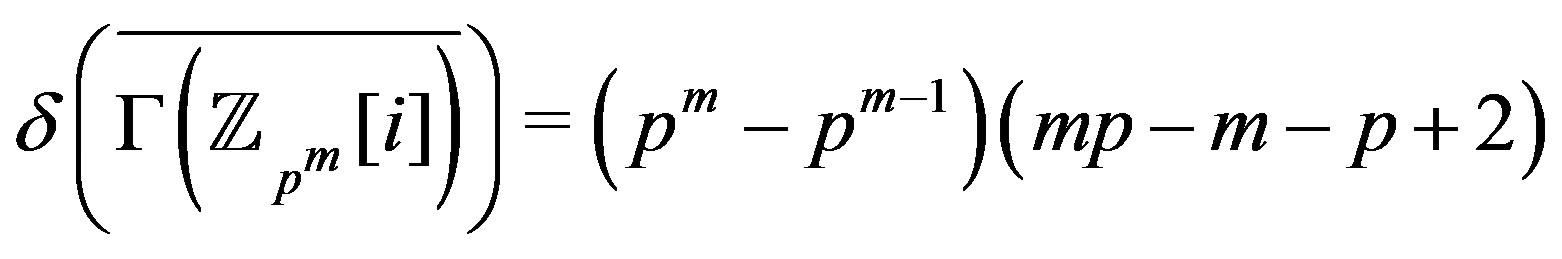 .
.
Therefore,
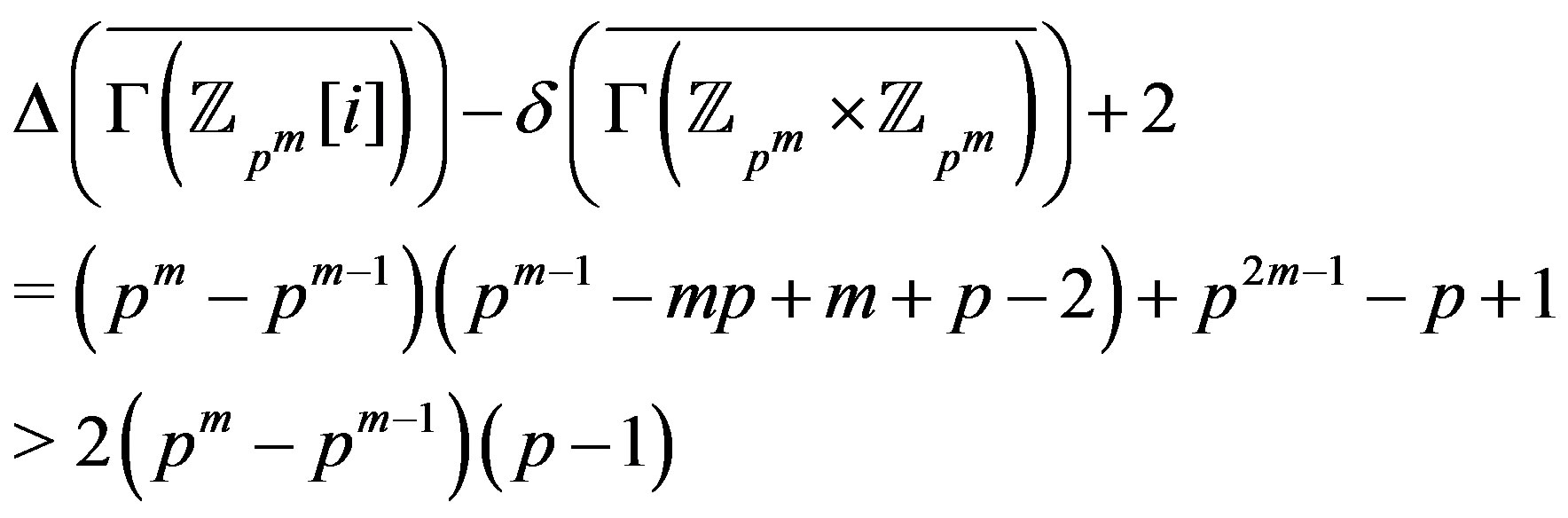 .
.
But the graph 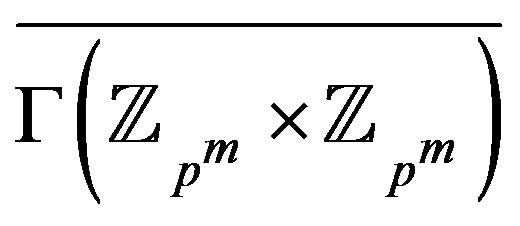 has only
has only
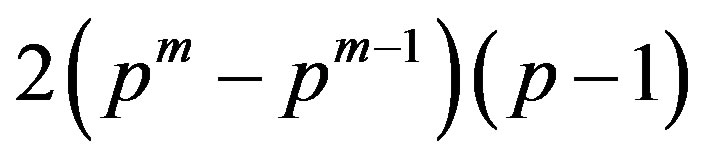 vertices of maximum degree. So,
vertices of maximum degree. So,
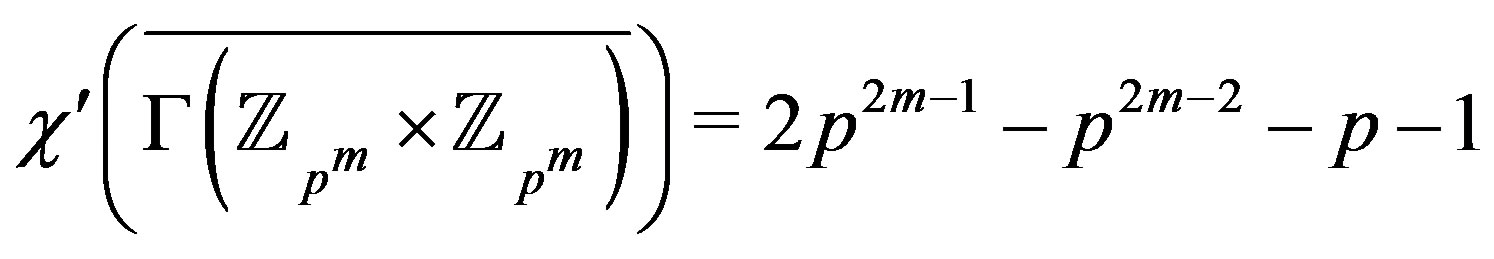 .
.
Since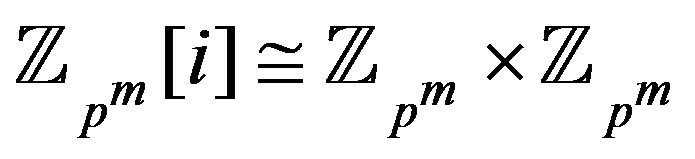 , the result holds.
, the result holds. 
Since the edge coloring of any graph leads to a vertex coloring of its line graph, we obtain the following.
Corollary 7.8 1) If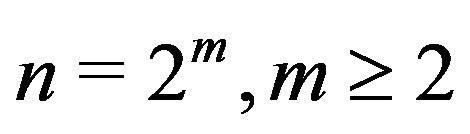 , then
, then
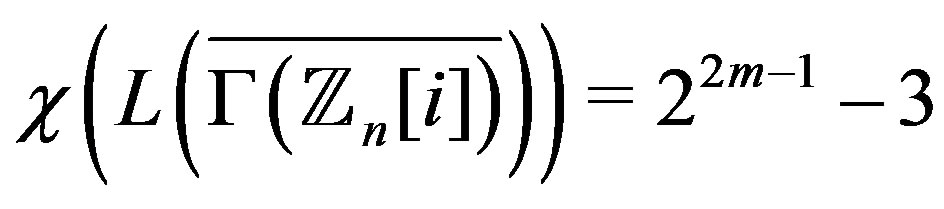 .
.
2) If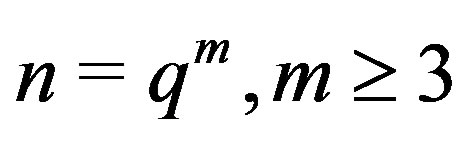 , then
, then
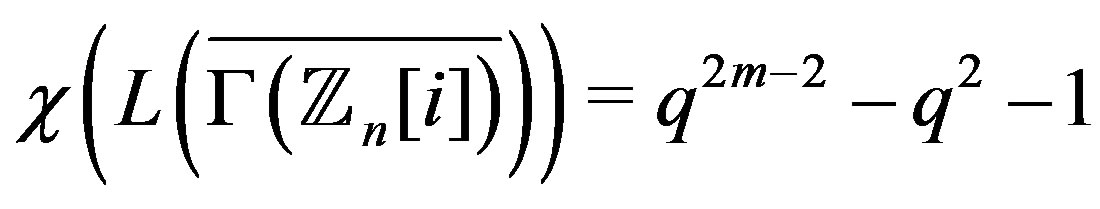 .
.
3) If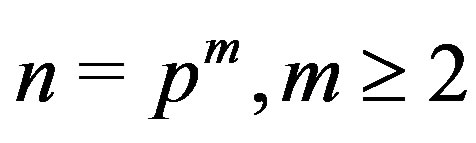 , then
, then
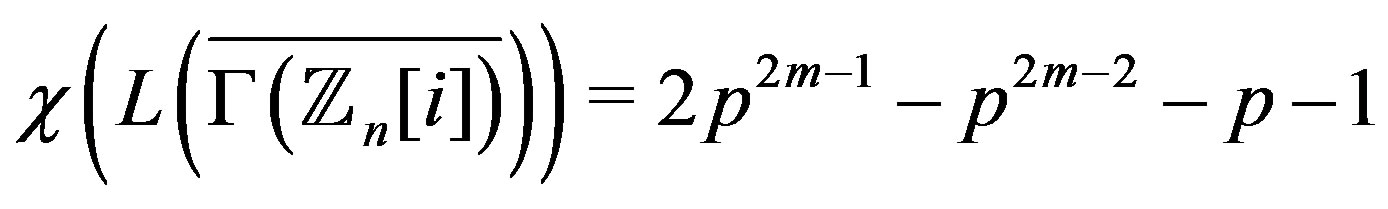 .
.
8. The Domination Number of 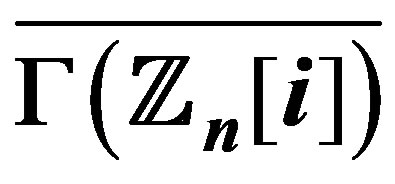
A subset  of the vertex set
of the vertex set 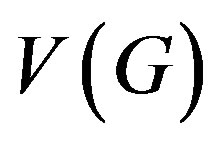 of a graph
of a graph 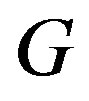 is a dominating set in
is a dominating set in 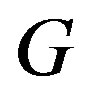 if each vertex of
if each vertex of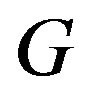 , not in
, not in , is adjacent to at least one vertex of
, is adjacent to at least one vertex of . The minimum cardinality of all dominating sets in
. The minimum cardinality of all dominating sets in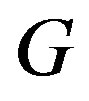 ,
, 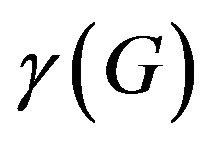 , is called the domination number of
, is called the domination number of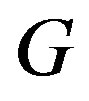 .
.
In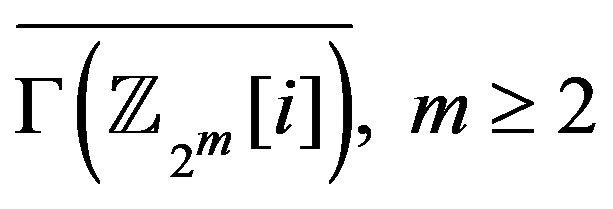 , the vertex
, the vertex 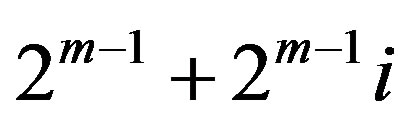 is an isolated vertex while the vertex
is an isolated vertex while the vertex 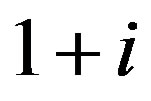 dominates all vertices in the second component. Therefore,
dominates all vertices in the second component. Therefore,
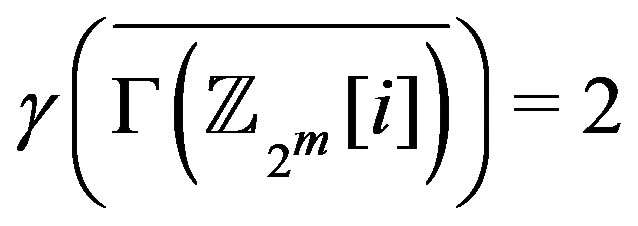 . The graph
. The graph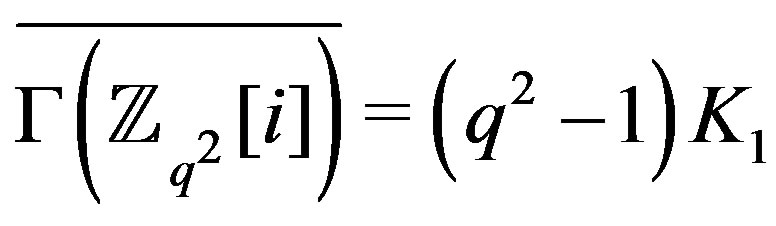 thus
thus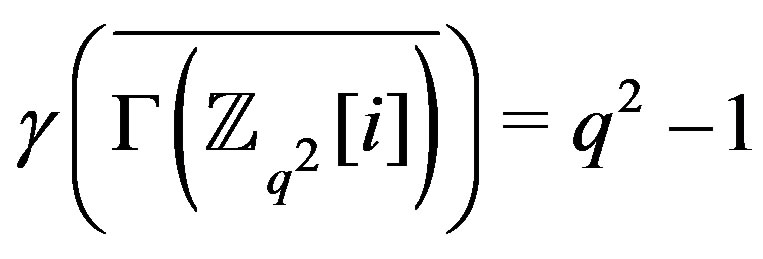 . In
. In 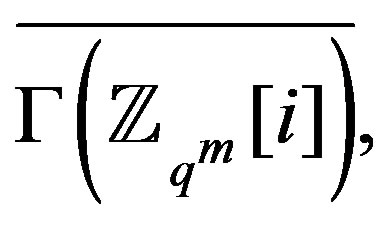
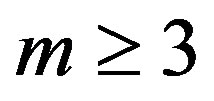 the vertices
the vertices 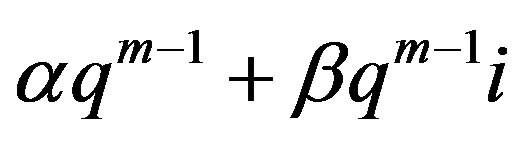 are isolated while the vertex
are isolated while the vertex  is adjacent to all other vertices in
is adjacent to all other vertices in
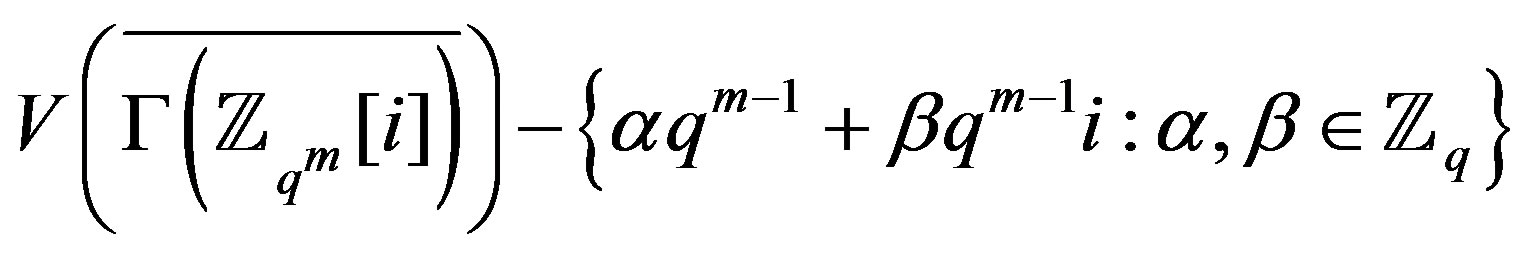 so
so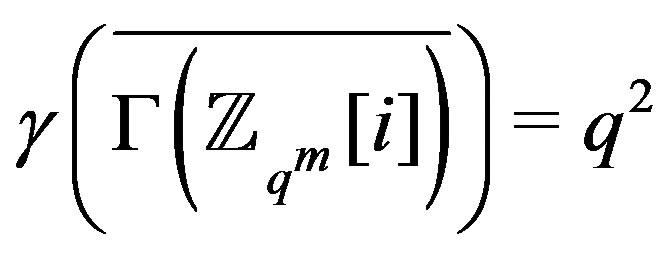 . Since
. Since

and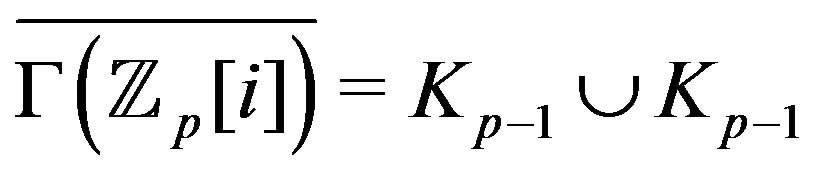 ,
,
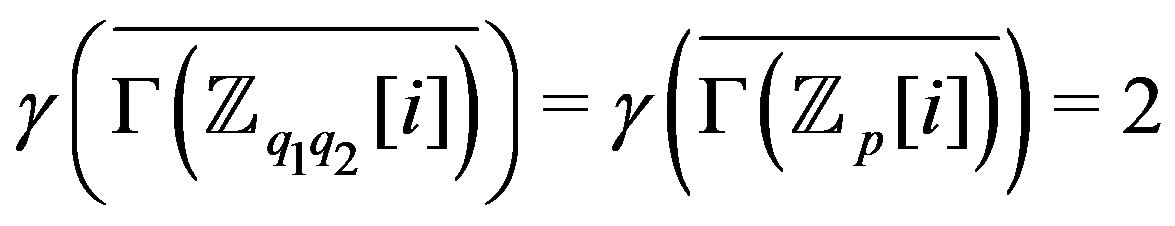 .
.
The set 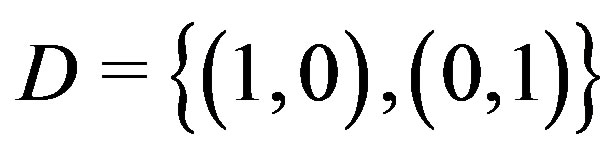 is a minimum dominating set for
is a minimum dominating set for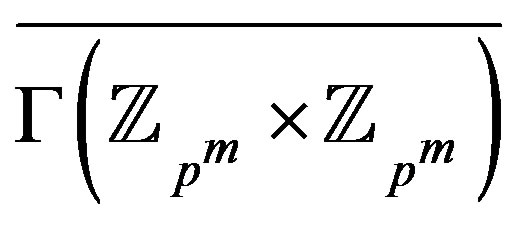 . And if
. And if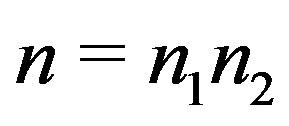 , where
, where
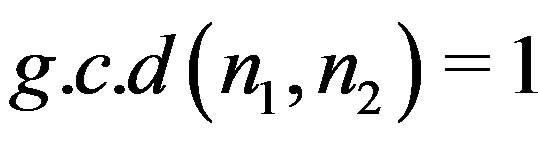 , then
, then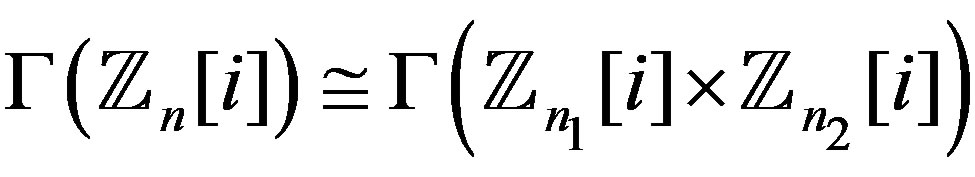 . This graph is connected and the set
. This graph is connected and the set 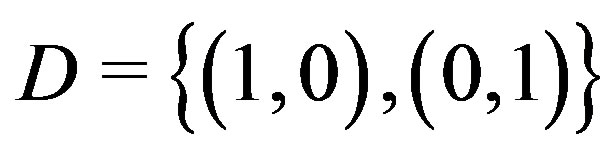 is a minimum dominating set for
is a minimum dominating set for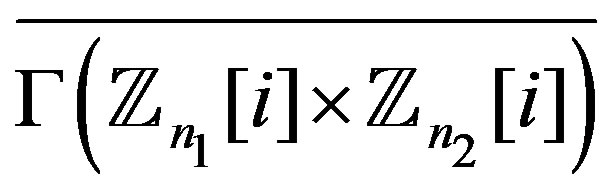 .
.
Theorem 8.1 1) If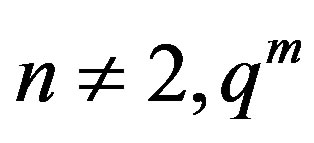 , then
, then
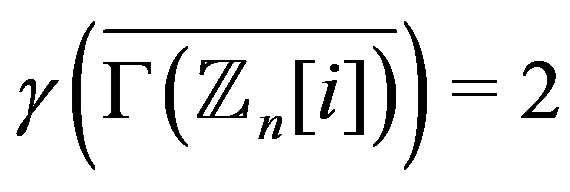 .
.
2) 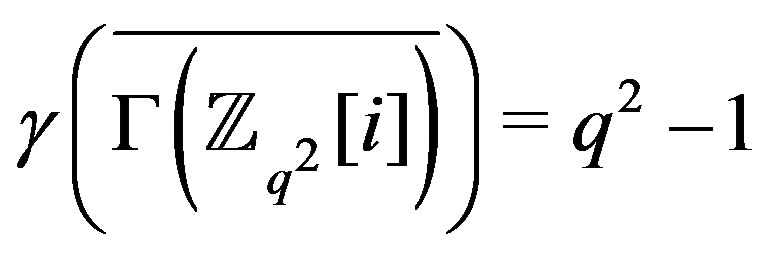 and
and
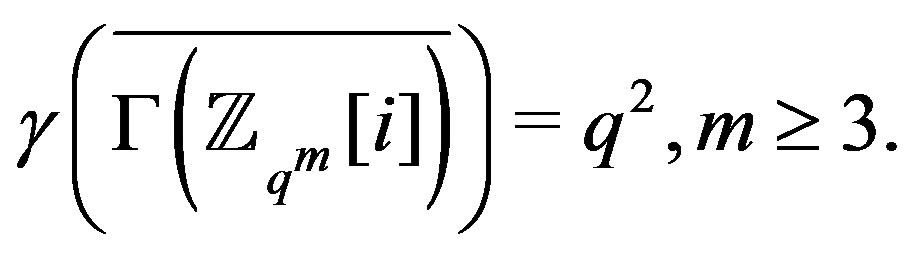
9. The Domination Number of 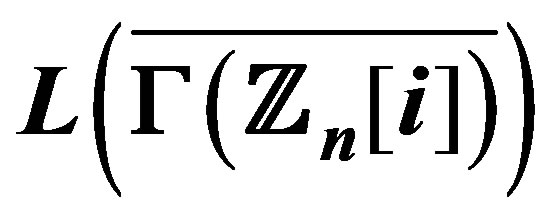
The independence number of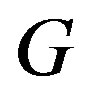 ,
, 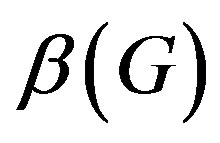 , is the maximum cardinality of all independent sets in
, is the maximum cardinality of all independent sets in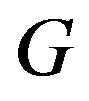 . A subset
. A subset  of the edge set
of the edge set 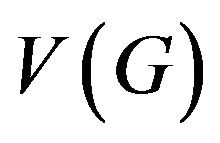 of a graph
of a graph 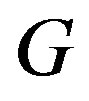 is an edge dominating set in
is an edge dominating set in 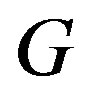 if each edge of
if each edge of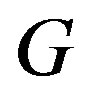 , not in
, not in , is adjacent to at least one edge of
, is adjacent to at least one edge of . The minimum cardinality of all edge dominating sets in
. The minimum cardinality of all edge dominating sets in ,
, 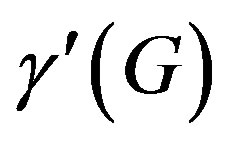 , is called the edge domination number of
, is called the edge domination number of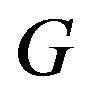 . The minimum cardinality of all independent edge dominating sets,
. The minimum cardinality of all independent edge dominating sets, 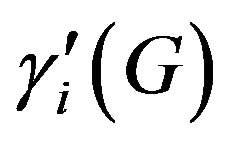 , is called the independence edge domination number of
, is called the independence edge domination number of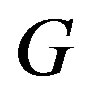 . The study of the domination number of the line graph of
. The study of the domination number of the line graph of 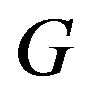 leads to the study of edge or line domination number of
leads to the study of edge or line domination number of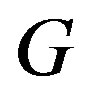 , i.e.
, i.e.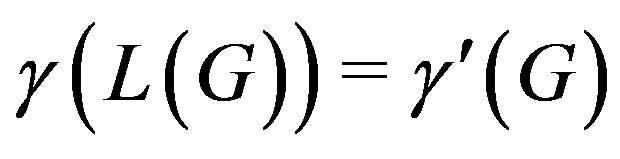 . On the other hand, for any graph
. On the other hand, for any graph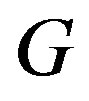 ,
, 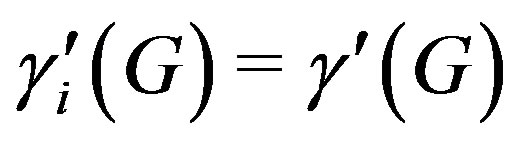 [15].
[15].
If 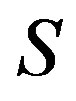 is an independent set in
is an independent set in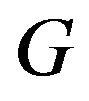 , then
, then 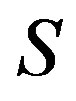 induces a complete graph in
induces a complete graph in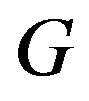 . While if
. While if 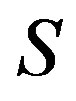 induces a complete graph in
induces a complete graph in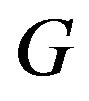 , then it is independent in
, then it is independent in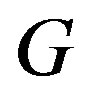 . Recall that
. Recall that 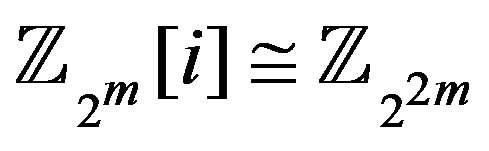 [2]. Then the sets,
[2]. Then the sets,
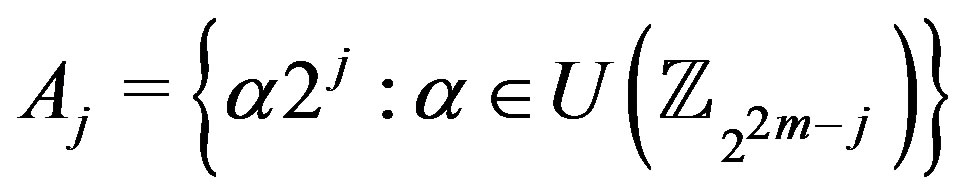 ,
, 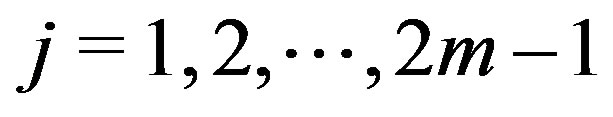 form a partition for the set
form a partition for the set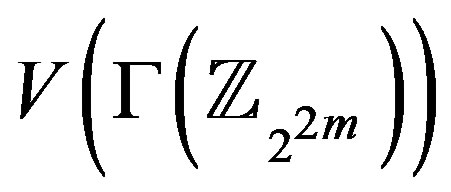 . Clearly, the set
. Clearly, the set 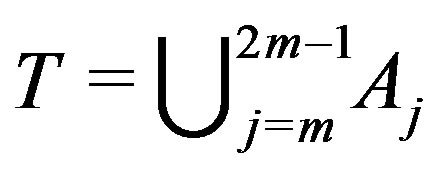 is the maximum independent set in
is the maximum independent set in
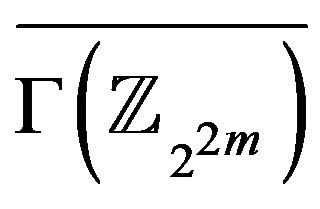 , while the set
, while the set 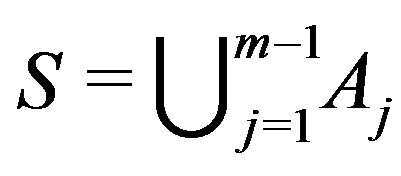 induces a maximum complete subgraph in
induces a maximum complete subgraph in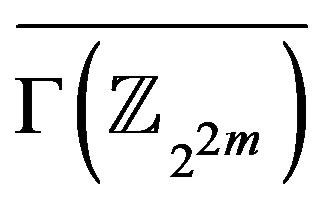 . There are some edges joining
. There are some edges joining 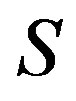 to
to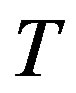 , no other adjacency exists in
, no other adjacency exists in
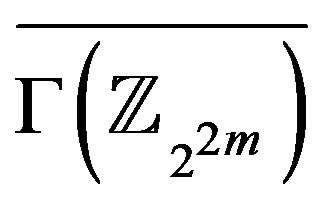 . Any edge dominating set for
. Any edge dominating set for 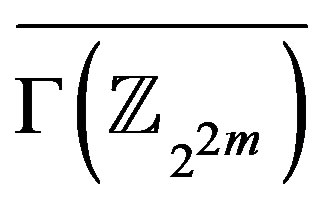 must contain at least
must contain at least 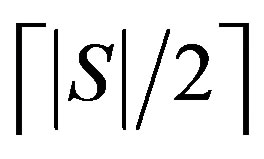 element in order to dominate
element in order to dominate
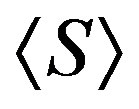 . On the other hand, this dominating set for
. On the other hand, this dominating set for 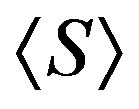 dominates all other edges in
dominates all other edges in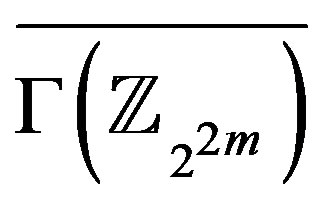 . Since
. Since
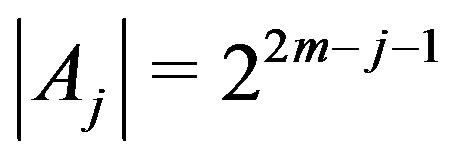 , then
, then 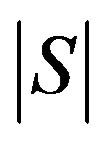 and
and , could easily be computed to get the following theorem.
, could easily be computed to get the following theorem.
Theorem 9.1 For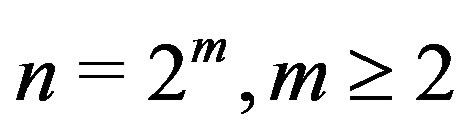 .
.
1)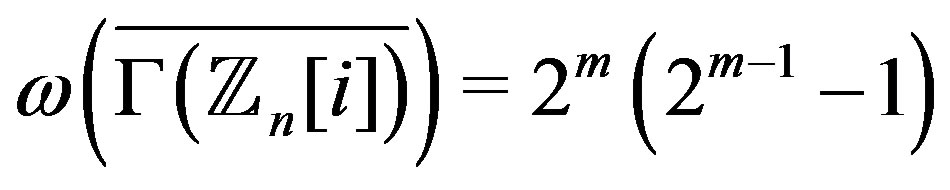 .
.
2)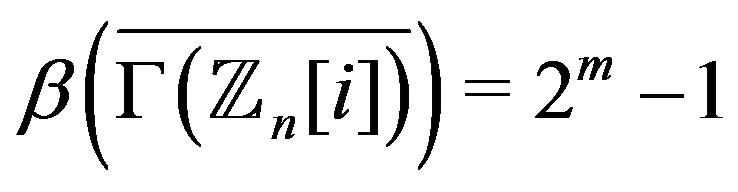 .
.
3) 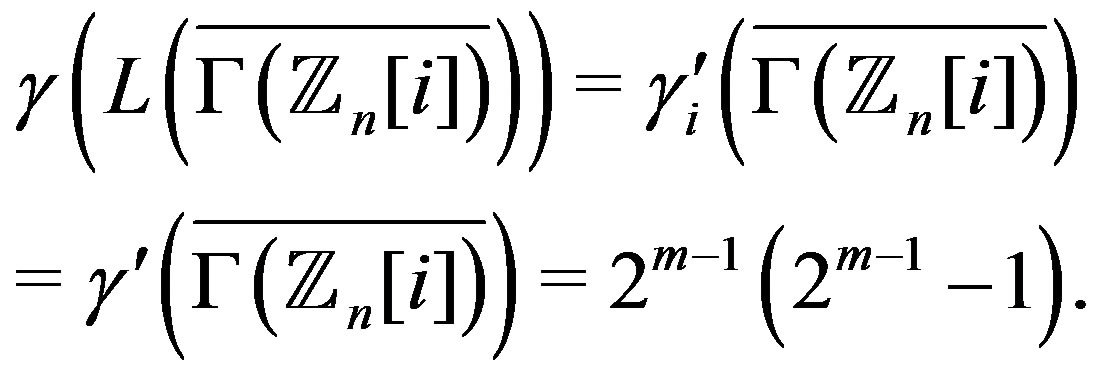
To study the graph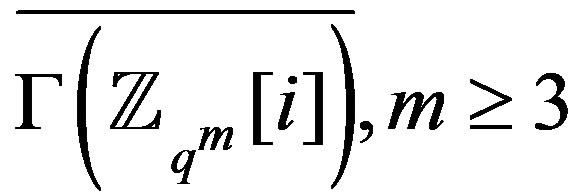 , consider the partition of
, consider the partition of 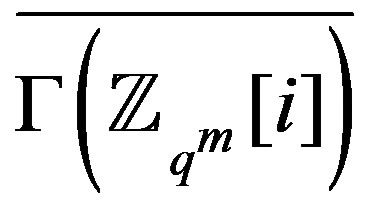 given by
given by
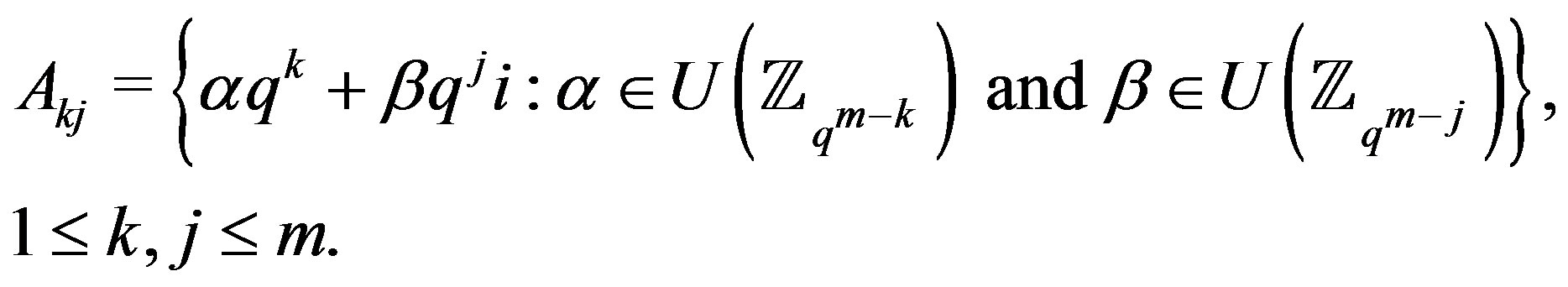
and not both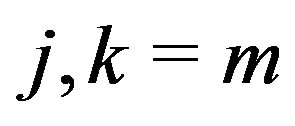 . The set
. The set
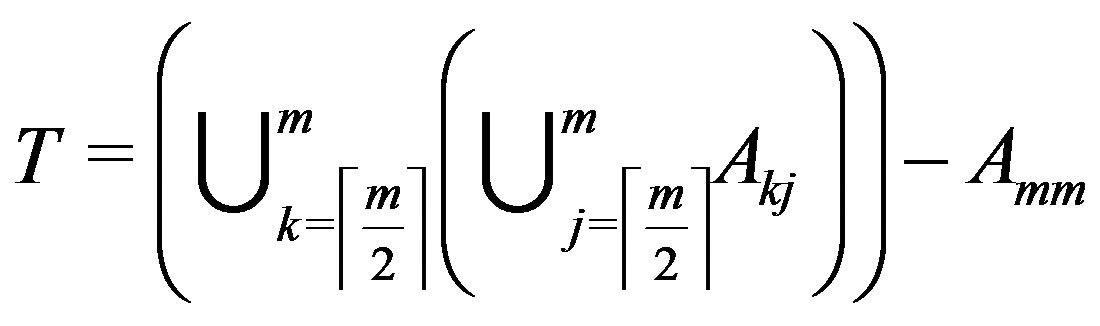 is the maximum independent set, while
is the maximum independent set, while 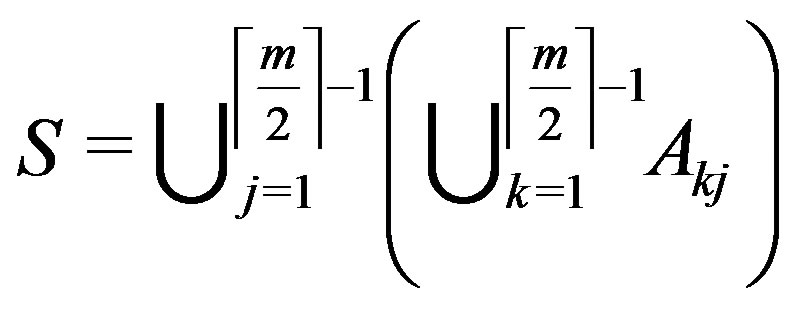 induces a maximum complete subgraph in
induces a maximum complete subgraph in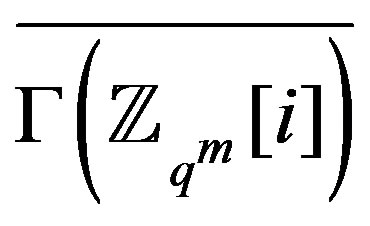 . There are some edges joining
. There are some edges joining 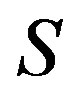 to
to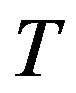 , and
, and  has no other adjacency. Easy calculations give
has no other adjacency. Easy calculations give
 when
when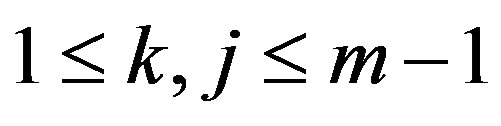 ,
,
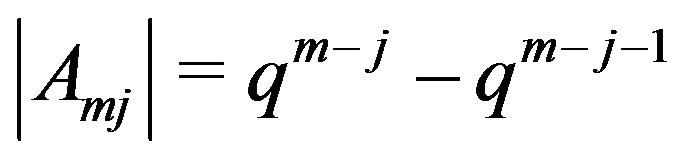 and
and 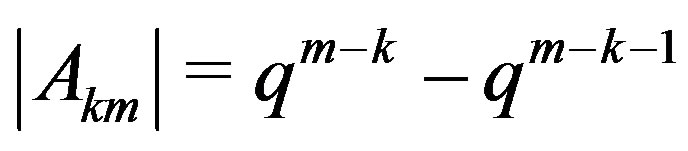 when
when
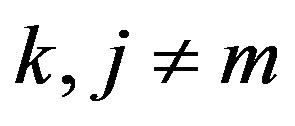 . While
. While 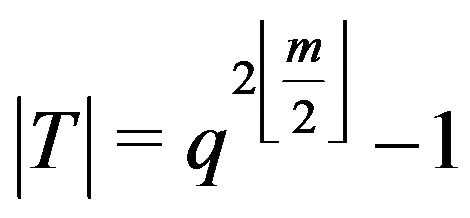 and
and
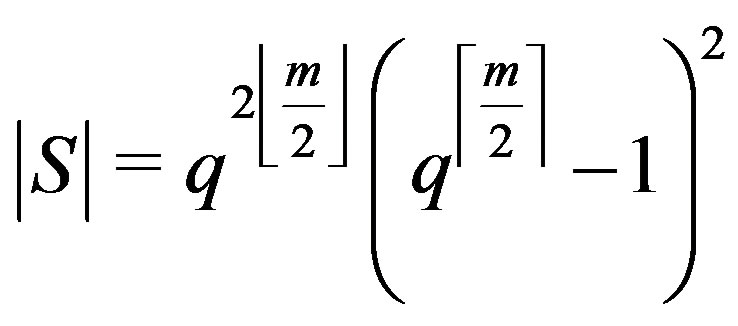 .
.
Thus we obtain the following theorem.
Theorem 9.2 If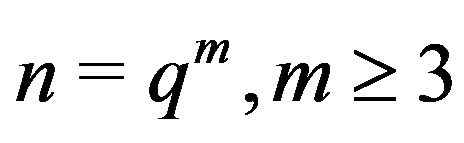 , then 1)
, then 1)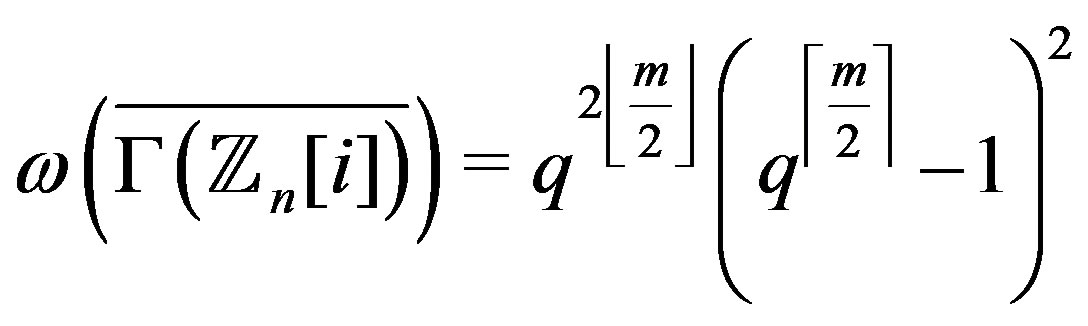 .
.
2) 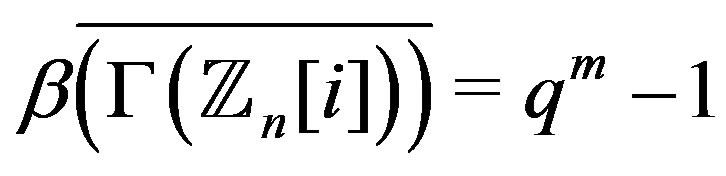 if
if 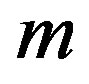 is even and
is even and 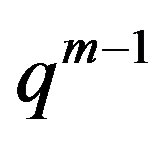 if
if 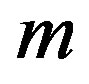 is odd.
is odd.
3) 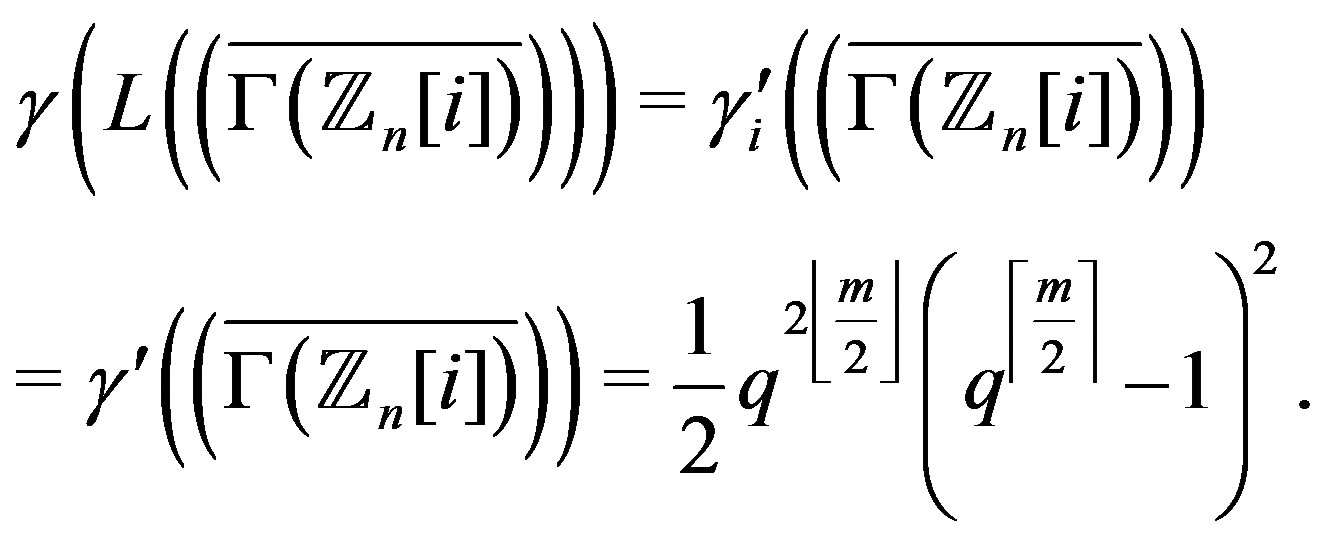
Now, we move to the case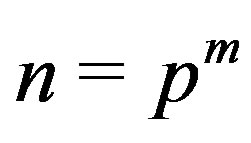 . Let
. Let
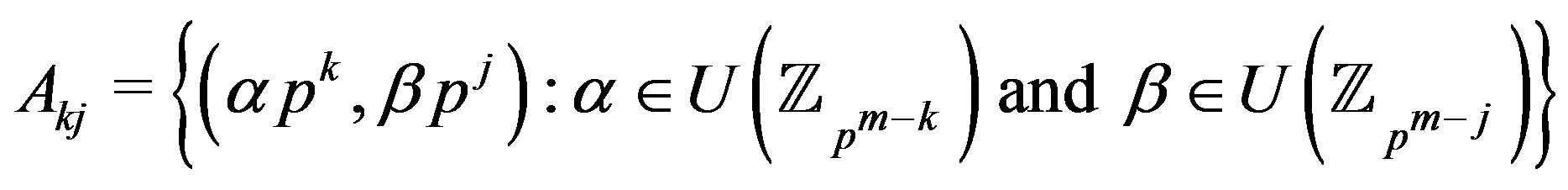 .
.
Clearly, the sets 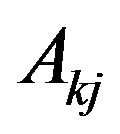 where
where 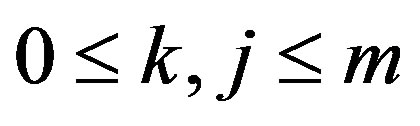 and not both
and not both 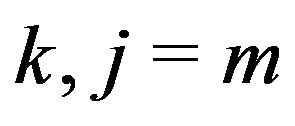 or 0, partition the vertices of
or 0, partition the vertices of
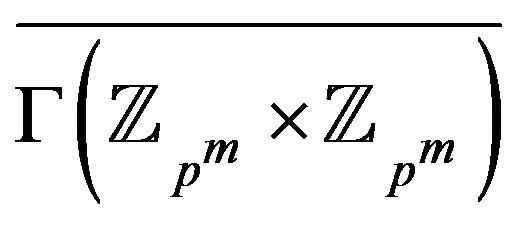 and
and . Let
. Let
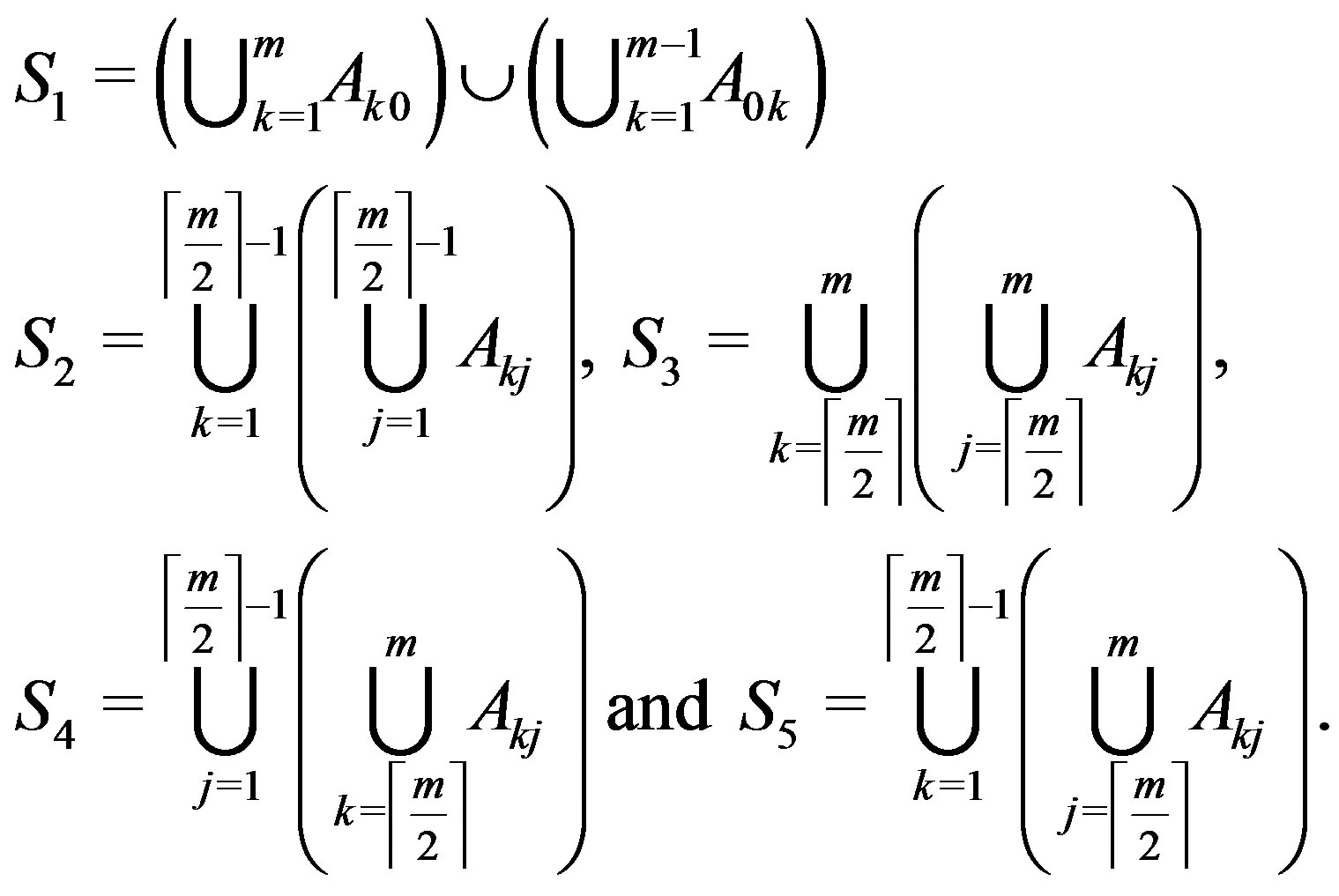
Note that  induces a complete graph in
induces a complete graph in
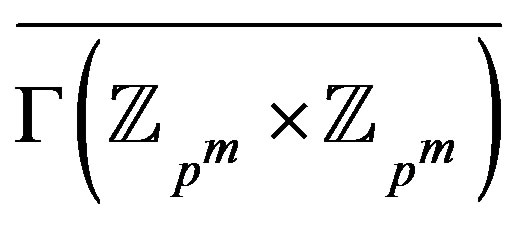 . Vertices in
. Vertices in  are adjacent to all vertices except some vertices in
are adjacent to all vertices except some vertices in 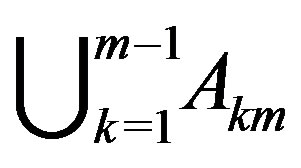 . Similarly, vertices in
. Similarly, vertices in 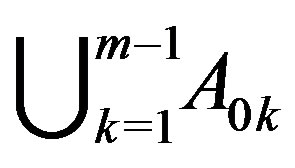 are adjacent to all vertices except some vertices in
are adjacent to all vertices except some vertices in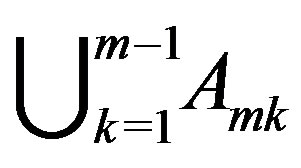 , and vertices in
, and vertices in 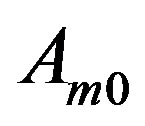 are adjacent to all vertices except vertices in
are adjacent to all vertices except vertices in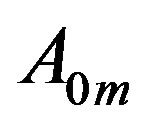 . On the other hand
. On the other hand 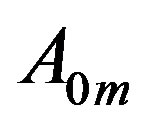 induces a complete subgraph and vertices in this set are adjacent to all other vertices except those of
induces a complete subgraph and vertices in this set are adjacent to all other vertices except those of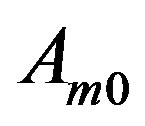 . Clearly
. Clearly 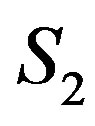 induces a complete subgraph. Vertices in
induces a complete subgraph. Vertices in 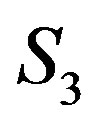 form an independent set, and are adjacent to some vertices in
form an independent set, and are adjacent to some vertices in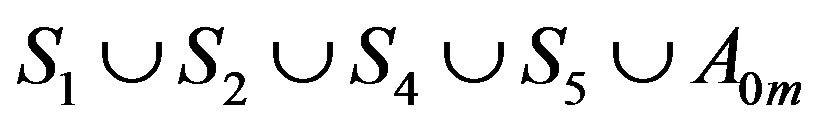 . Each of
. Each of 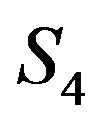 and
and 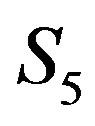 induces a complete subgraph and are adjacent to some vertices in
induces a complete subgraph and are adjacent to some vertices in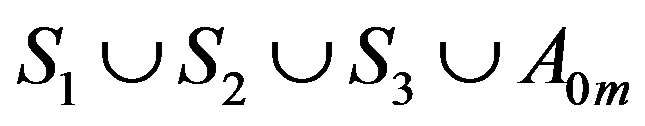 . Besides, there are some edges between
. Besides, there are some edges between 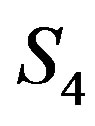 and
and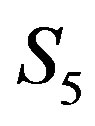 . On the other hand,
. On the other hand,
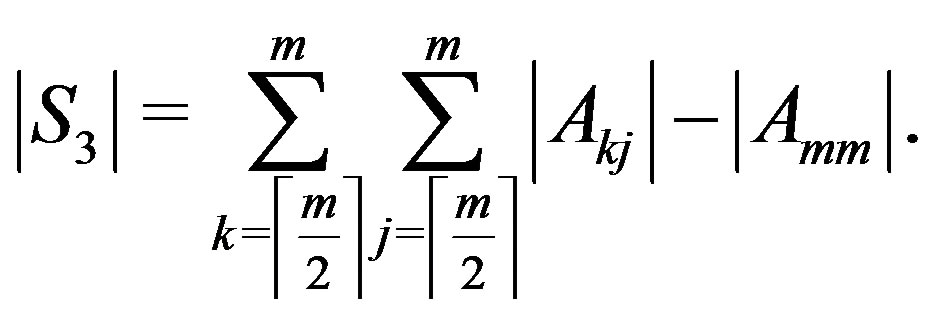
The above argument shows that
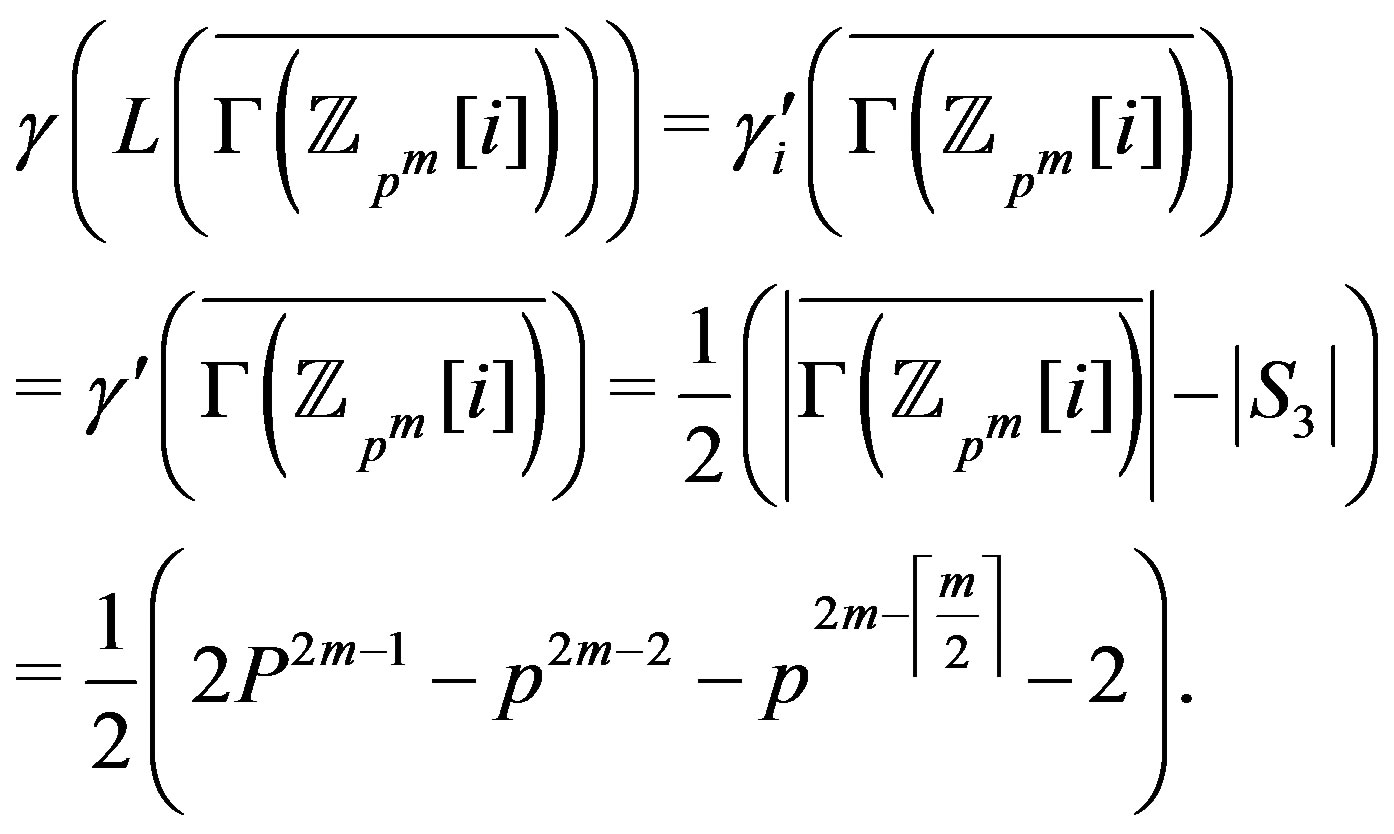
10. The Degree of the Vertices in 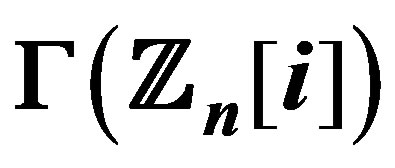 and
and 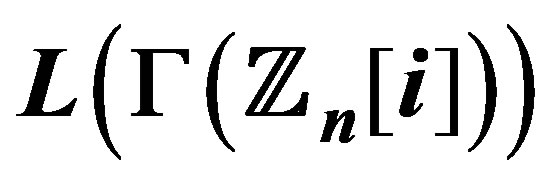
Now, we determine the cardinality of the annihilator of the element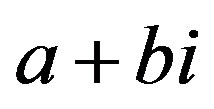 ,
, 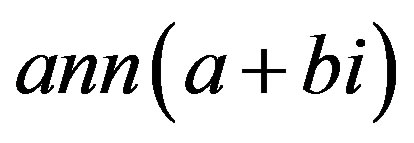 in
in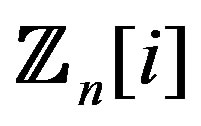 . This helps find the degree of each vertex in
. This helps find the degree of each vertex in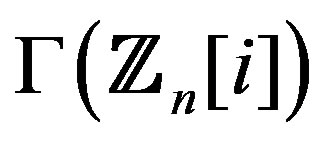 , its complement, as well as the degree of each vertex in their corresponding line graphs.
, its complement, as well as the degree of each vertex in their corresponding line graphs.
Theorem 10.1 If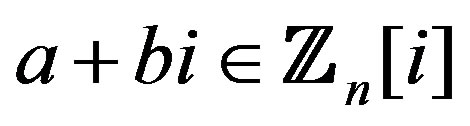 , then
, then
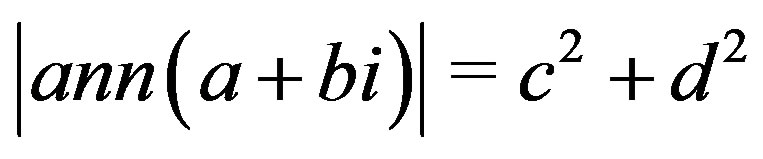 where
where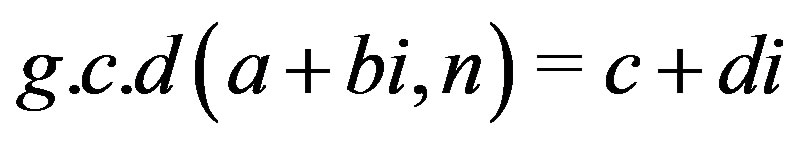 .
.
Proof. Let 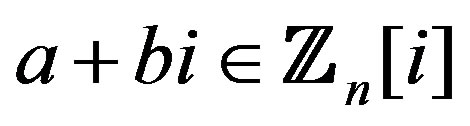 and
and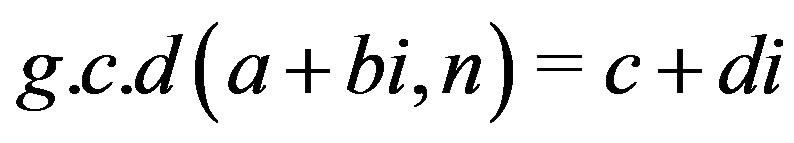 . Then
. Then
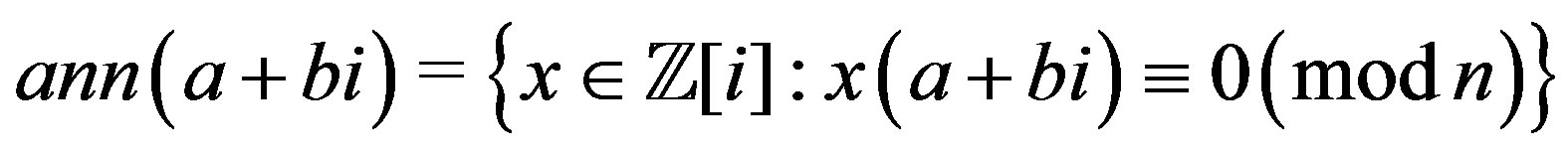 .
.
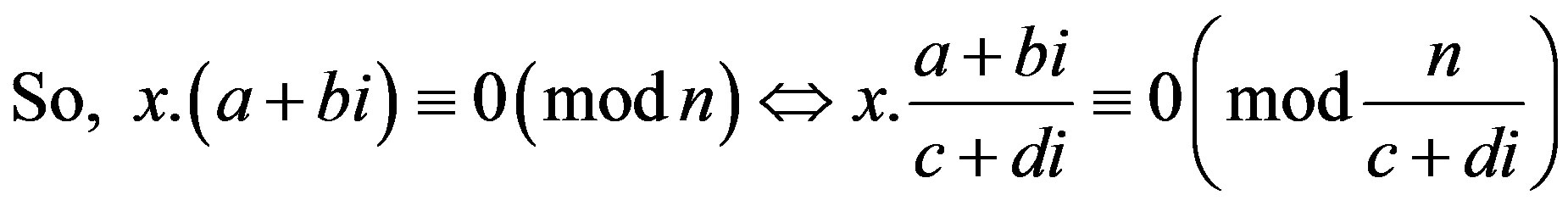 .
.
But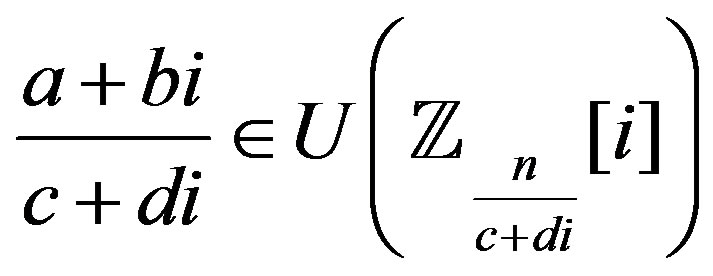 . So,
. So, 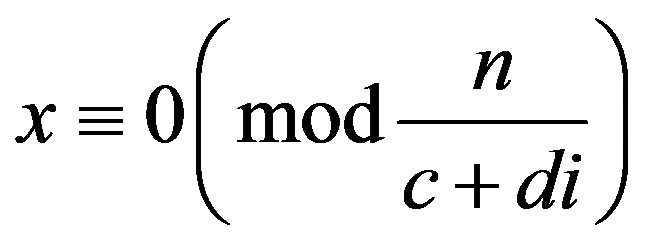
and hence there exists 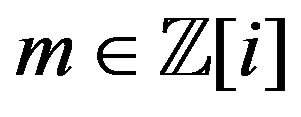 such that
such that .
.
Since 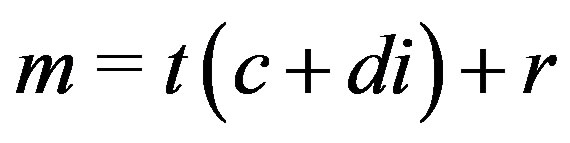 where
where 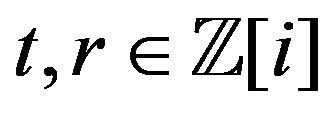 and the norm of
and the norm of 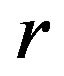 is less than the norm of
is less than the norm of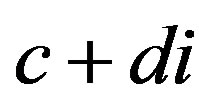 ,
,
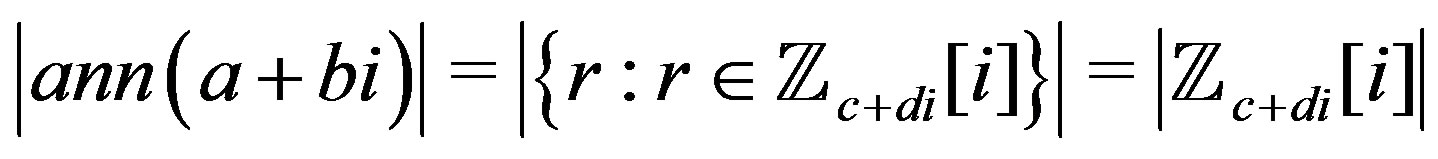 . By Theorem 2 of [7],
. By Theorem 2 of [7], 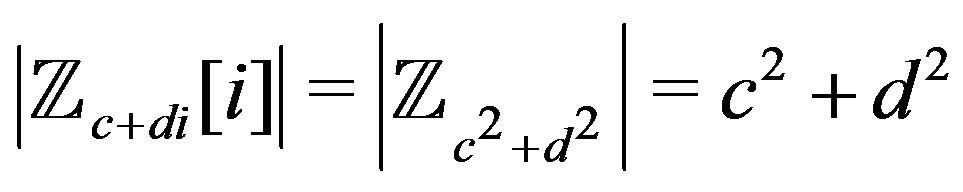 , so the result holds.
, so the result holds. 
Theorem 10.2 Let 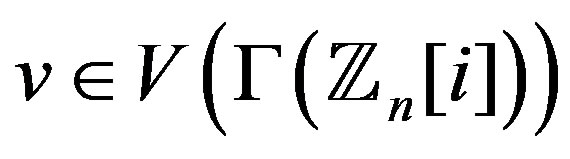 and
and 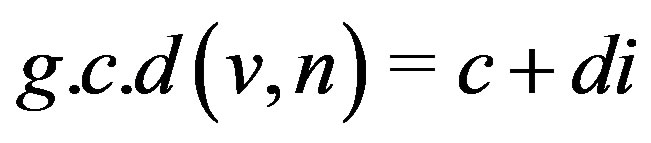 . Then
. Then
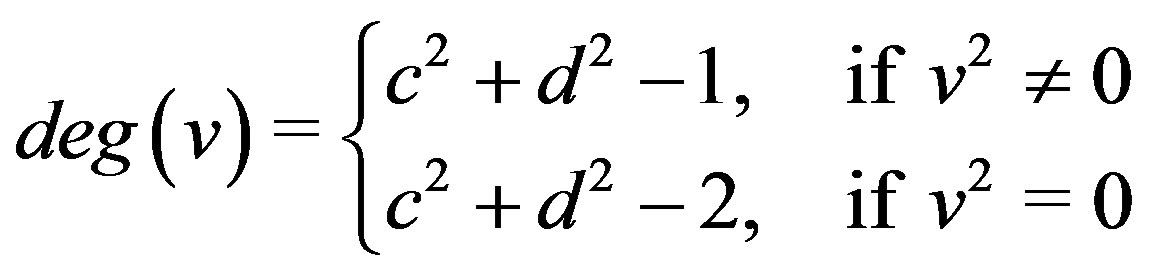 .
.
The order of 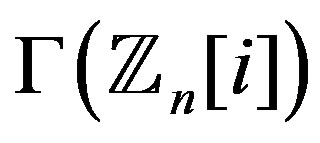 can be easily computed using formulas given in [1]. Thus we can find the degree of each vertex in the complement of
can be easily computed using formulas given in [1]. Thus we can find the degree of each vertex in the complement of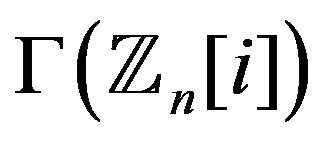 , here we give the degree of each vertex in the line graph of
, here we give the degree of each vertex in the line graph of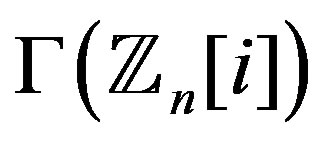 , an analogous formula for the degree of vertices in
, an analogous formula for the degree of vertices in 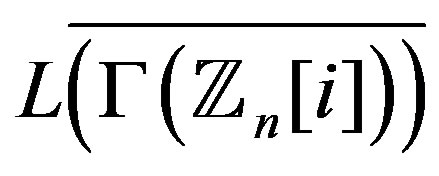 could be obtained.
could be obtained.
Corollary 10.3 Let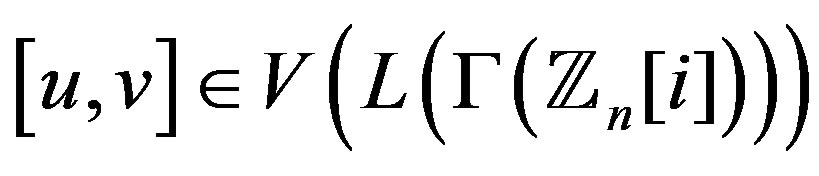 ,
,
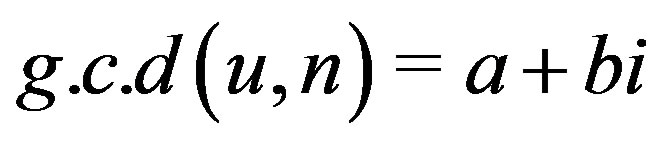 and
and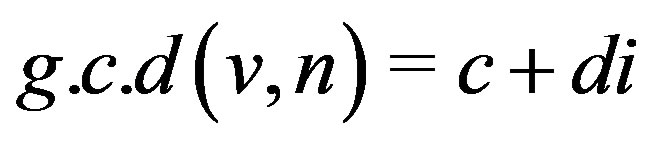 . Then
. Then
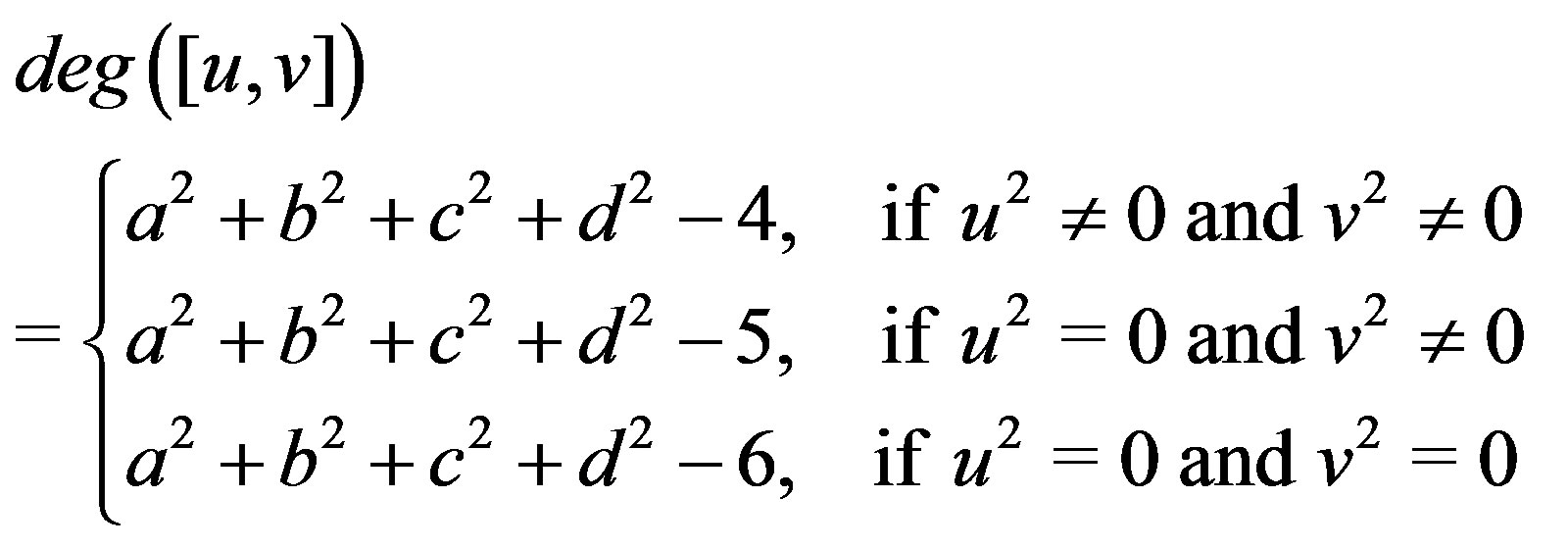 .
.
Proof. Note that, for any graph 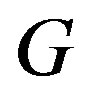 and
and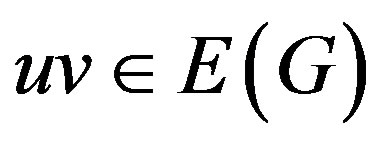 ,
,
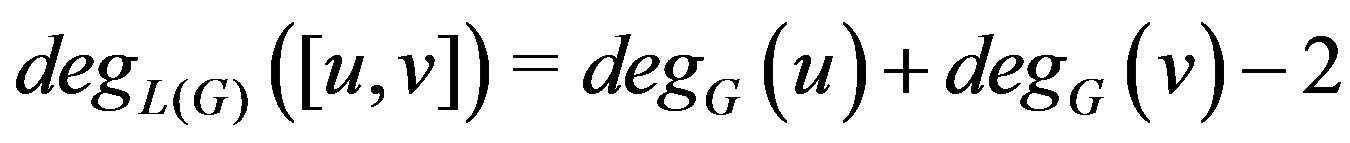 .
. 
In the following we determine the degree of every vertex in the graphs 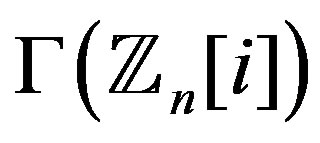 when
when 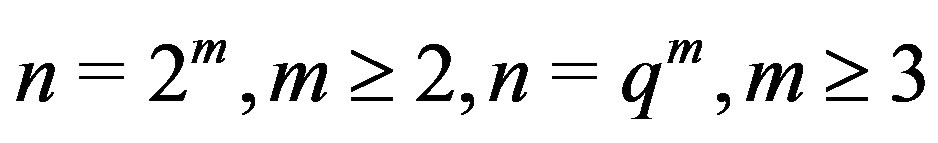 and
and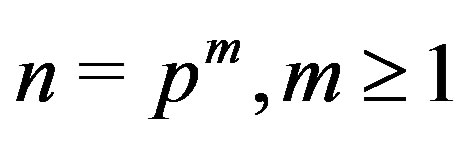 .
.
Theorem 10.4 Let 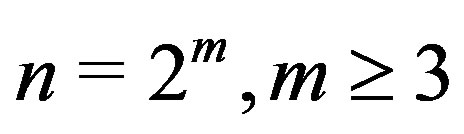 and
and 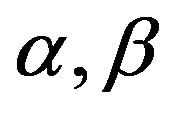 are odd. Then in
are odd. Then in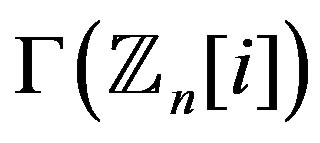 1)
1)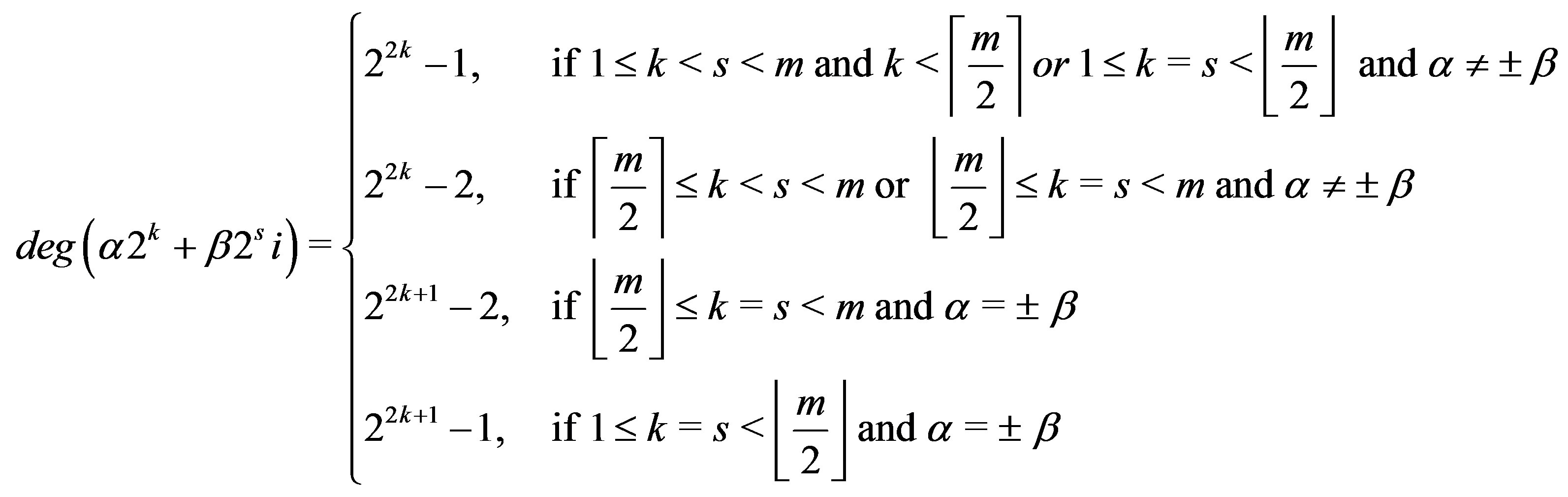 .
.
2) 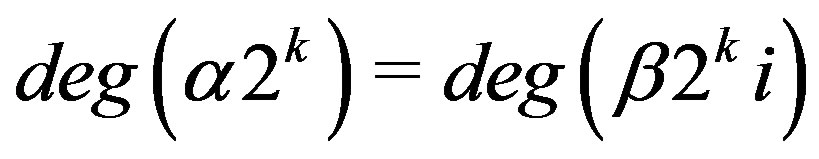
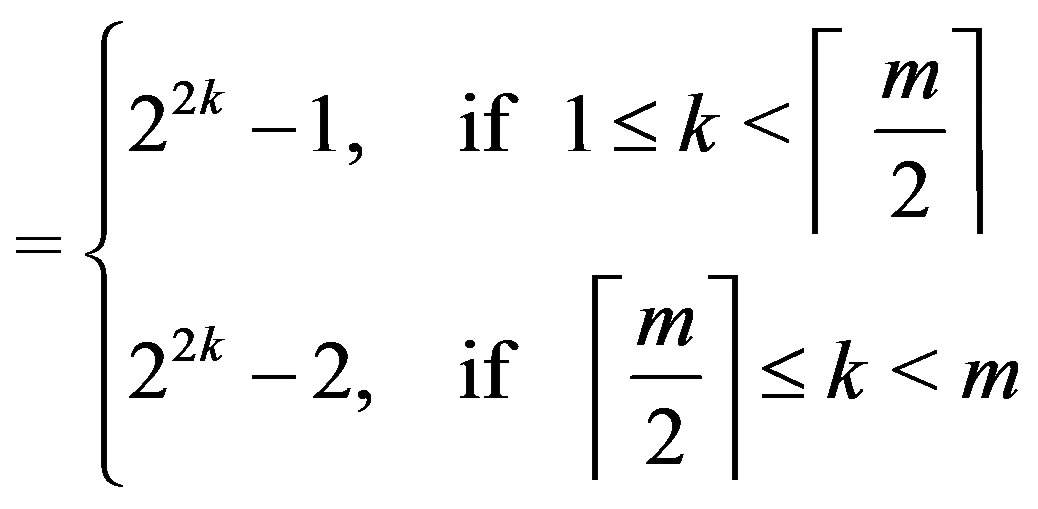 .
.
3)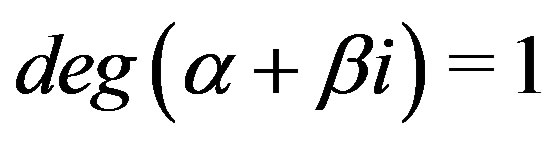 .
.
Proof. 1) Note that, 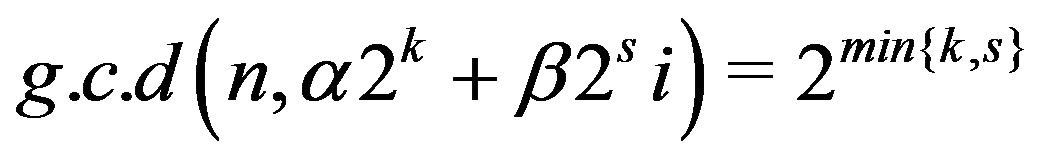 if
if
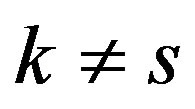 or
or 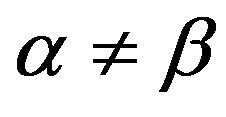 and
and 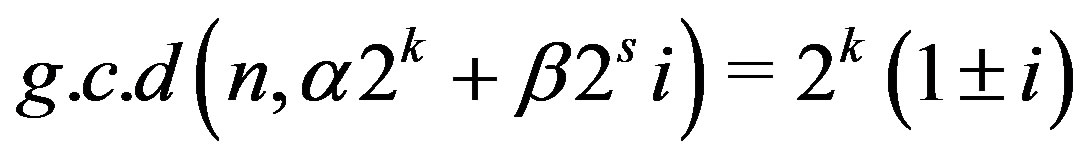
if and only if 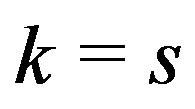 and
and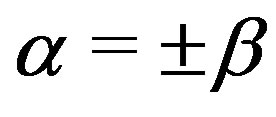 . Moreover
. Moreover
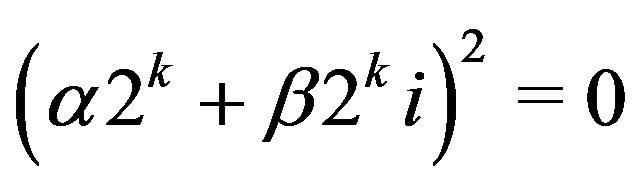 if and only if
if and only if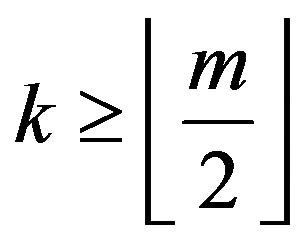 .
.
2) Obvious.
3) Note that if  are odd, then
are odd, then 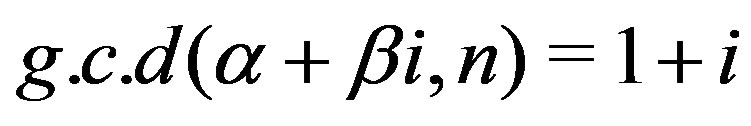 .
. 
Theorem 10.5 Let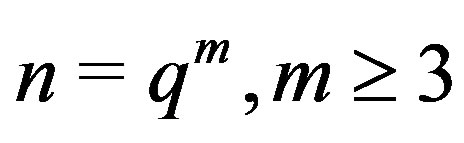 ,
, 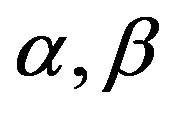 are relatively prime with
are relatively prime with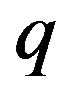 . Then in
. Then in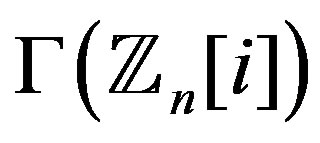 ,
,
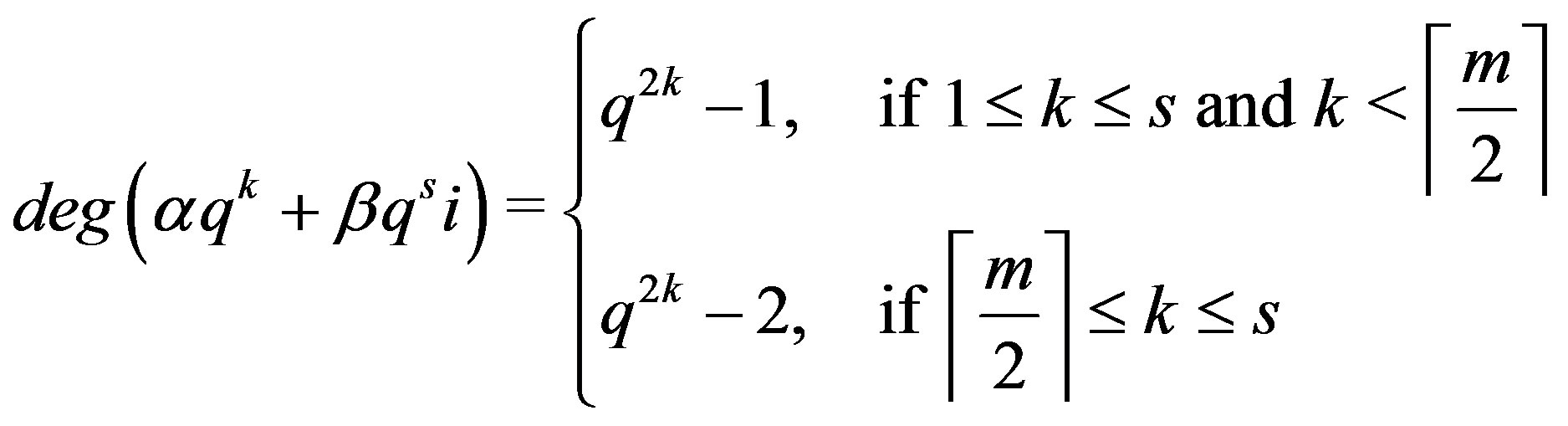 .
.
Theorem 10.6 Let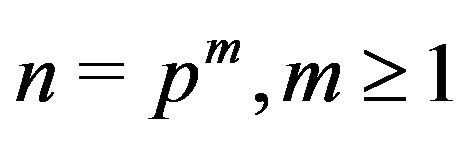 ,
, 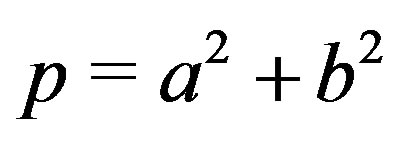 and
and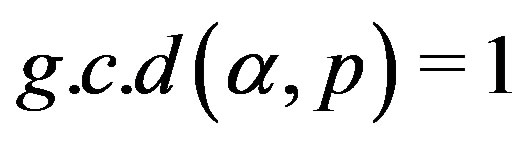 . Then in
. Then in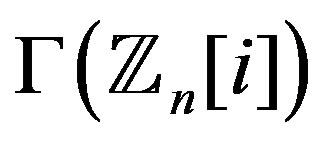 ,
,
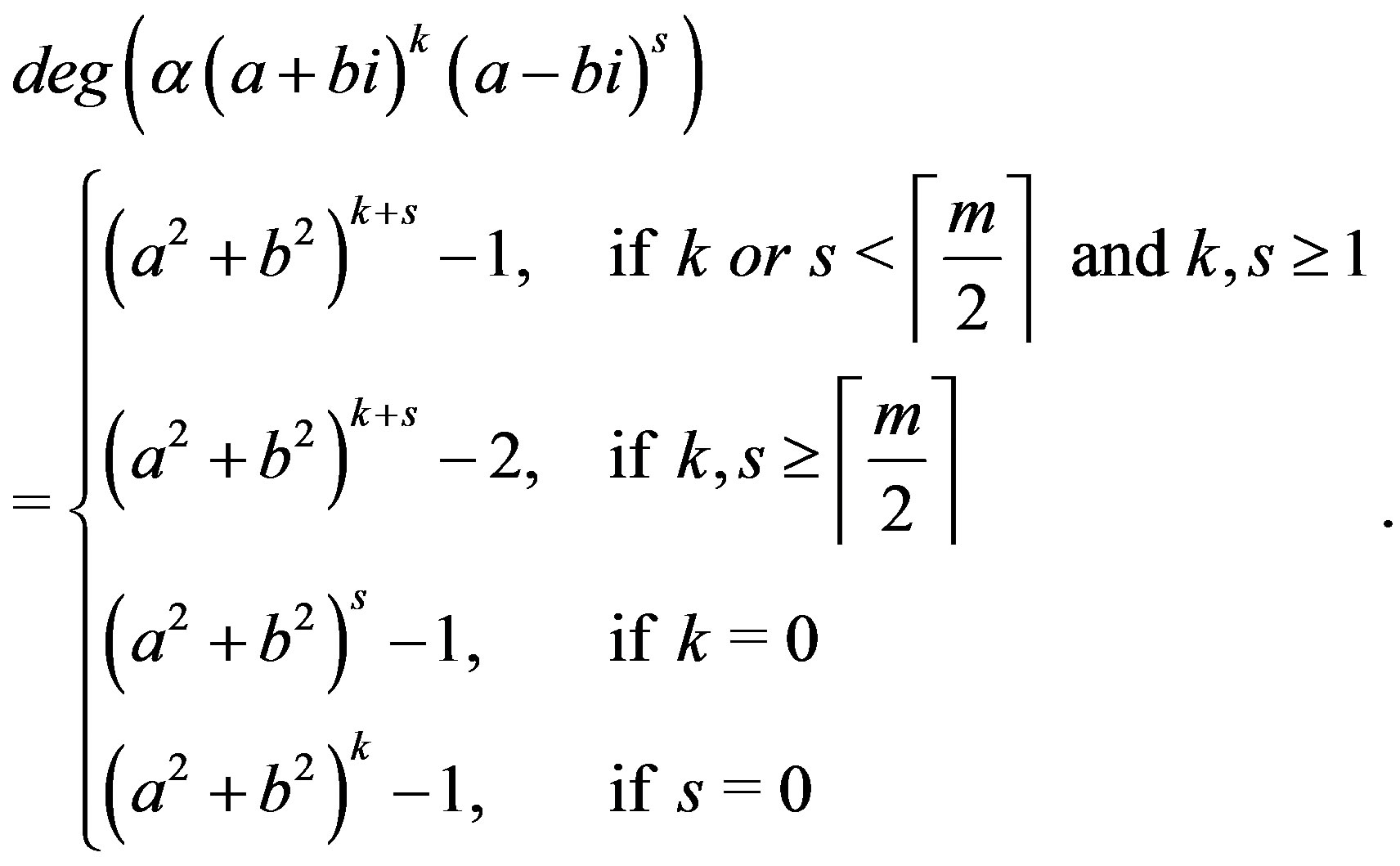
11. When is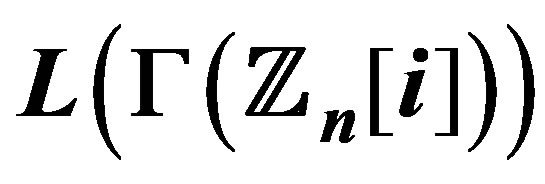 ,
, 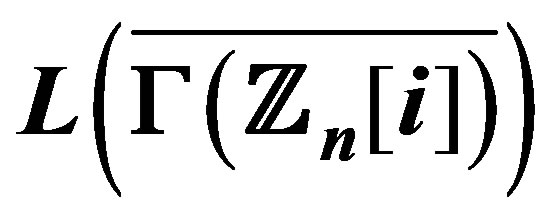 Regular?
Regular?
A graph 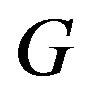 in which all vertices have the same degree is called regular graph.
in which all vertices have the same degree is called regular graph.
Regularity of 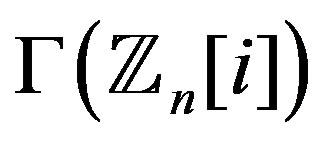 was studied in [1]. However, we provide our own proof, since it comes as an immediate consequence of Theorem 10.2. Clearly, if
was studied in [1]. However, we provide our own proof, since it comes as an immediate consequence of Theorem 10.2. Clearly, if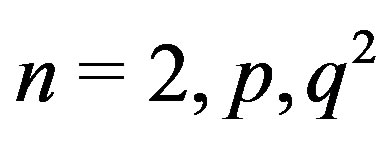 , then
, then 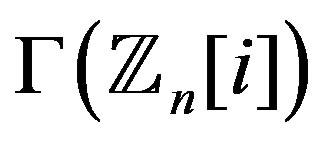 is regular. If
is regular. If 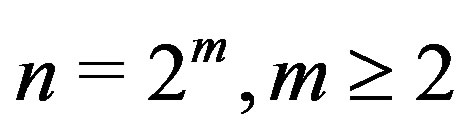 or
or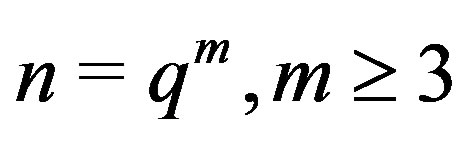 , then the graph
, then the graph 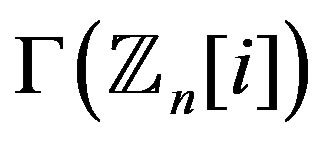 has a vertex which is adjacent to all other vertices and it is not complete graph, thus
has a vertex which is adjacent to all other vertices and it is not complete graph, thus 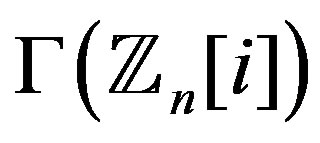 is not regular.
is not regular.
Now, we show that 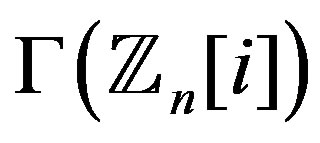 is regular if and only if
is regular if and only if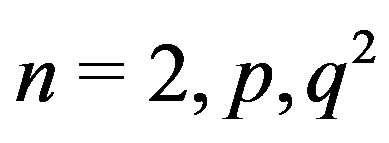 .
.
Theorem 11.1 If 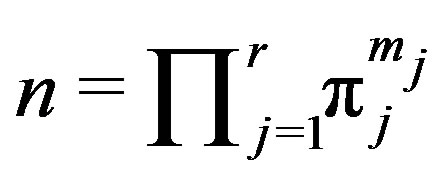 where
where 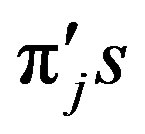 are distinct Gaussian primes and
are distinct Gaussian primes and 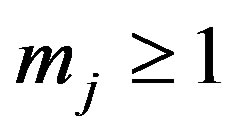 and
and 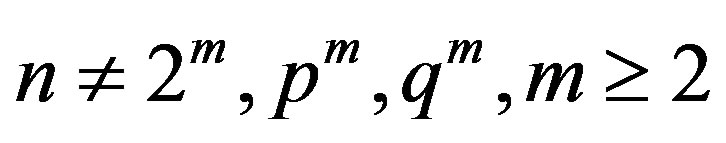 , then
, then 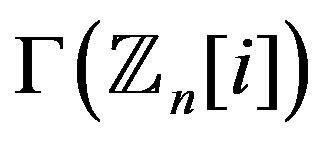 is not regular.
is not regular.
Proof. Choose two vertices  and
and  such that
such that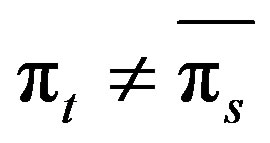 , then
, then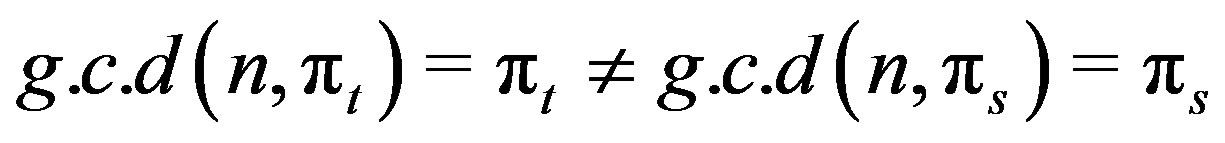 . So, the result follows.
. So, the result follows. 
Next, we discuss regularity of the graph
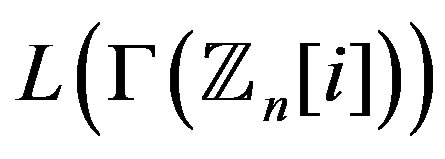 and
and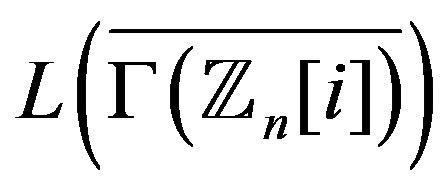 . Clearly, if
. Clearly, if 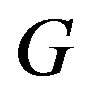 is regular, then
is regular, then 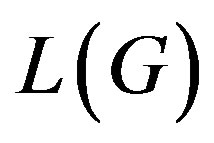 is also regular, so if
is also regular, so if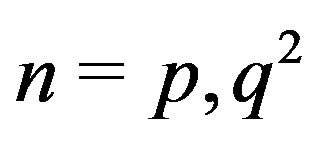 , then the graph
, then the graph 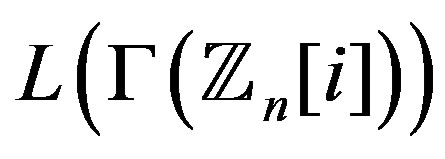 is regular. On the other hand, if
is regular. On the other hand, if 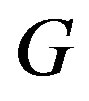 is the complete bipartite graph
is the complete bipartite graph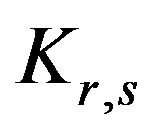 , then
, then
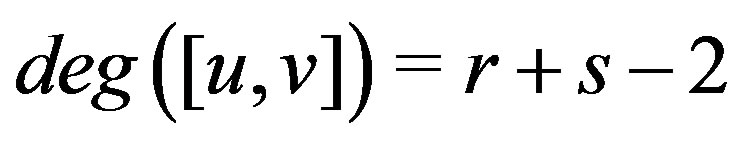 for all vertices in
for all vertices in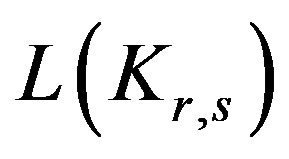 . Thus
. Thus
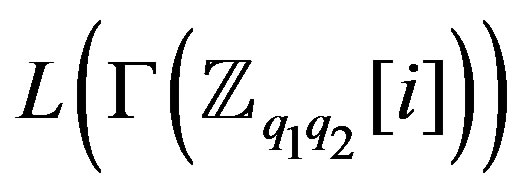 is regular. While
is regular. While 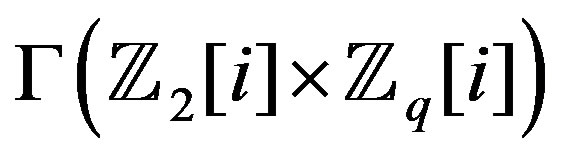 is a bipartite graph with partite sets
is a bipartite graph with partite sets
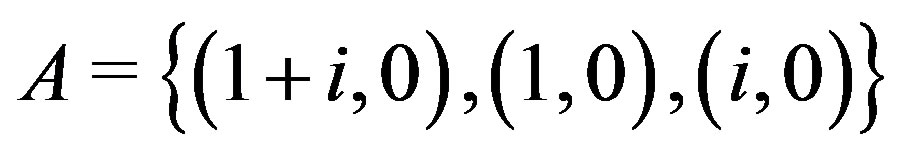 and
and
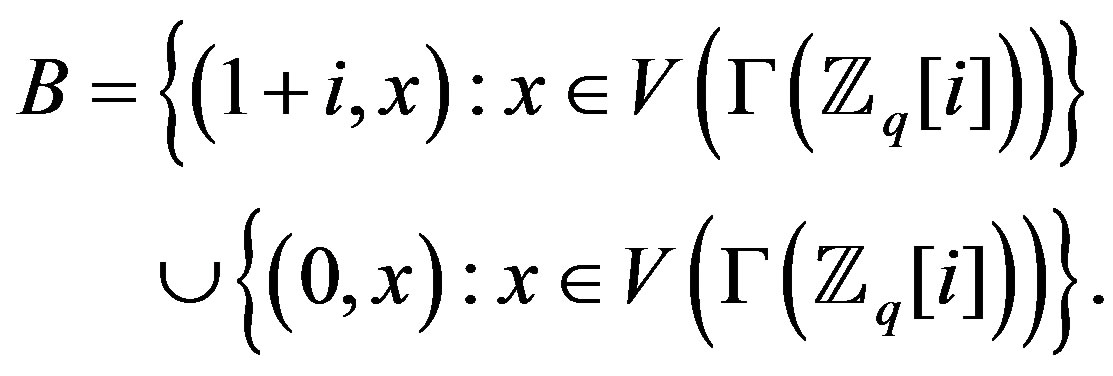
Moreover, 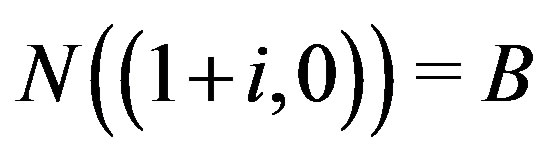 ,
, 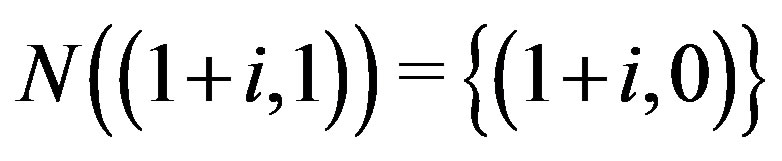 and
and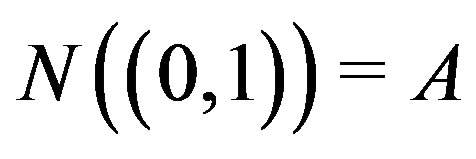 . Thus,
. Thus,
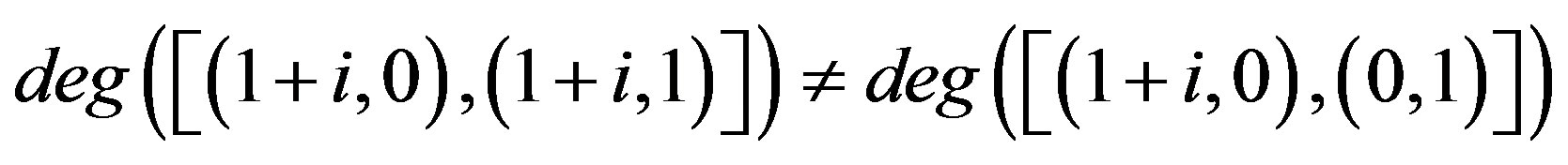 and hence,
and hence, 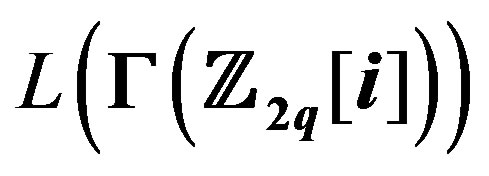 is not regular.
is not regular.
Theorem 11.2 If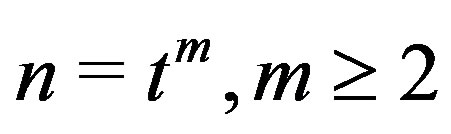 ,
, 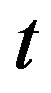 is a prime and
is a prime and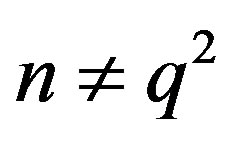 , then the graph
, then the graph 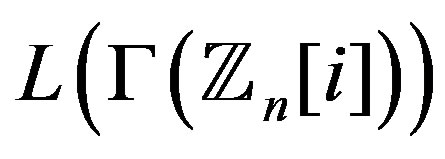 is not regular.
is not regular.
Proof. If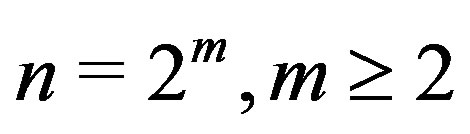 , then
, then
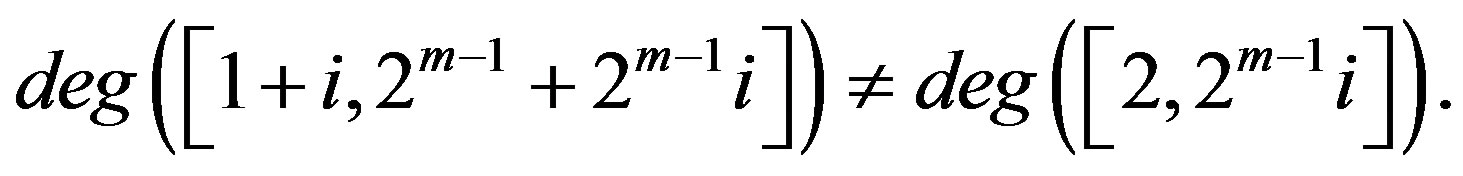 If
If
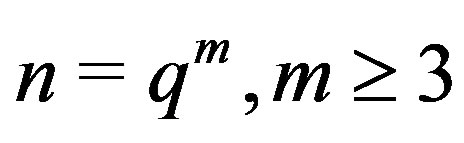 , then
, then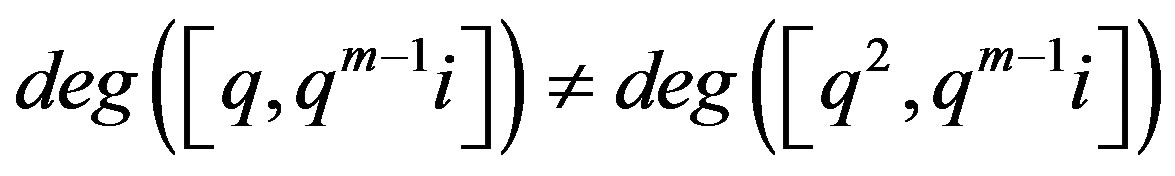 .
.
And if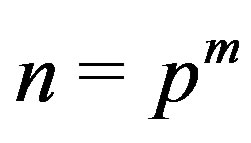 ,
, 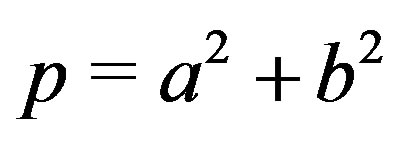 ,
, 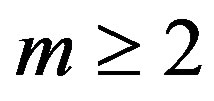 , then
, then

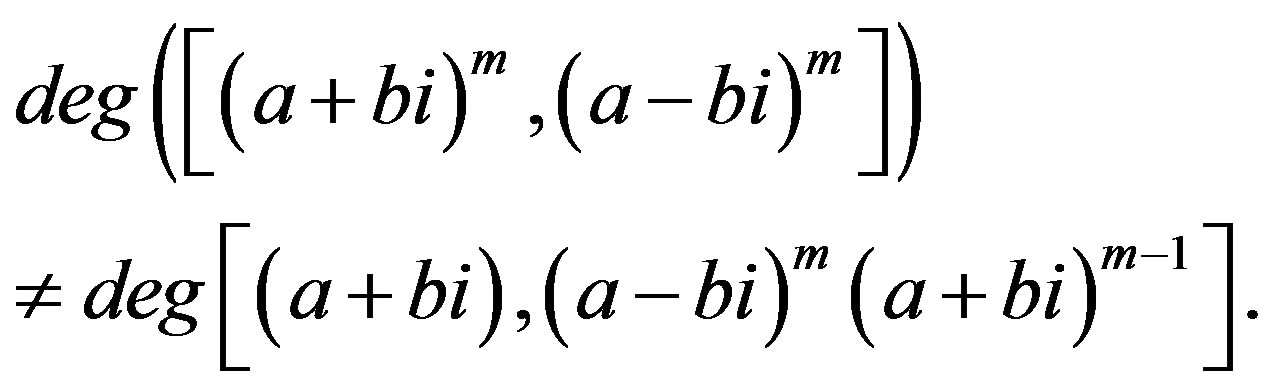
Theorem 11.3 Let 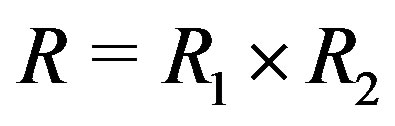 where
where 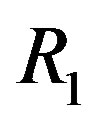 and
and 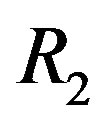 are commutative rings with unity with at least one of them is not ID. Then
are commutative rings with unity with at least one of them is not ID. Then 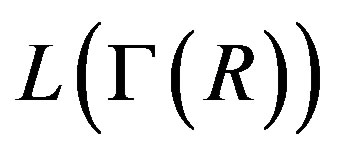 is not regular.
is not regular.
Proof. Suppose that 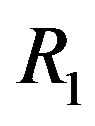 is not ID and
is not ID and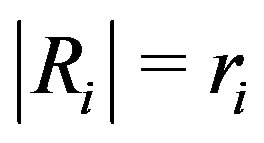 , for
, for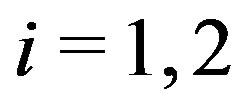 . Let
. Let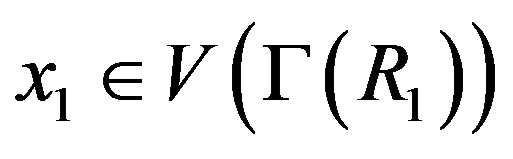 . If
. If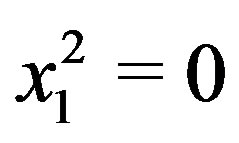 , then
, then

and 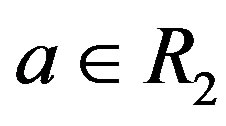 if
if
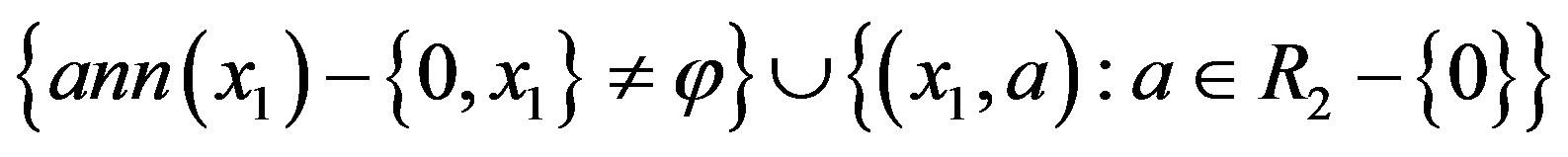 , hence
, hence
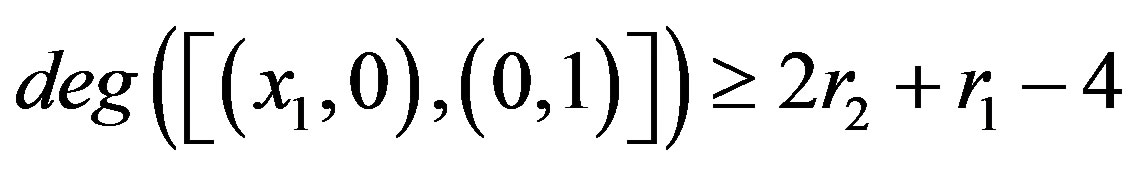 . And if
. And if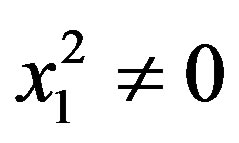 ,
,
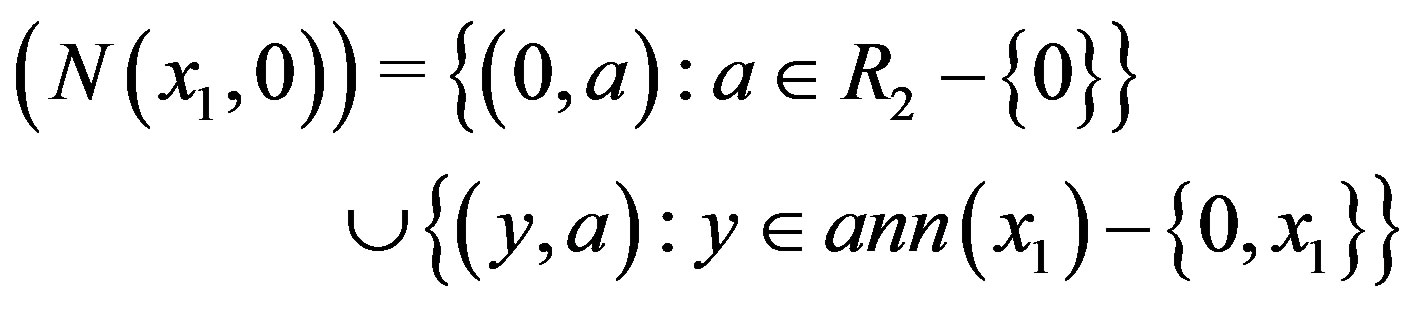
and 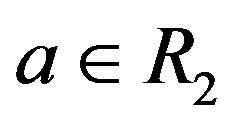 if
if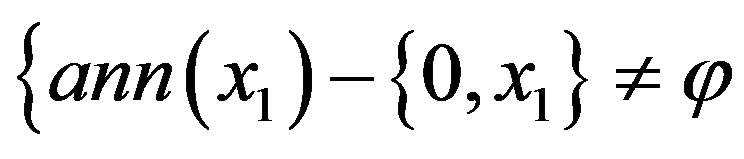 , hence
, hence
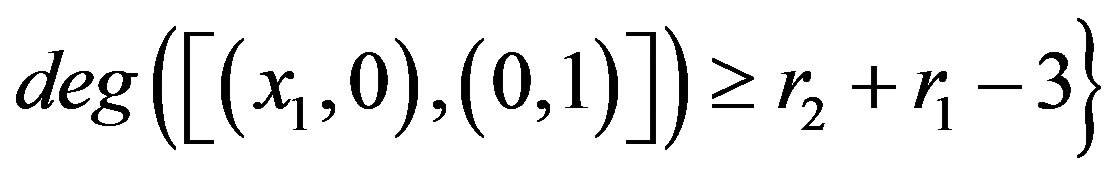 . But
. But
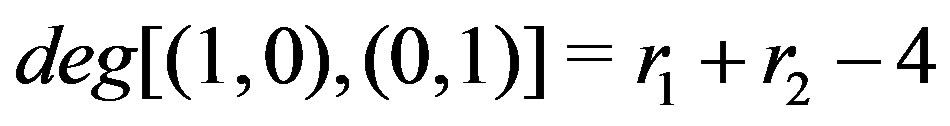 . So
. So 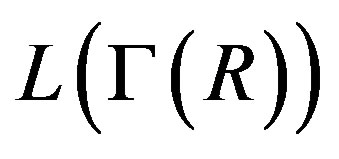 is not regular.
is not regular. 
So as a consequence of Theorem 11.2 and Theorem 11.3, we conclude the following.
Theorem 11.4 The graph 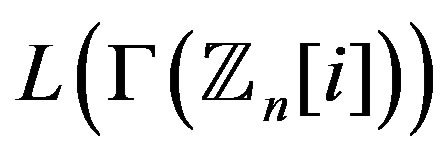 is regular if and only if
is regular if and only if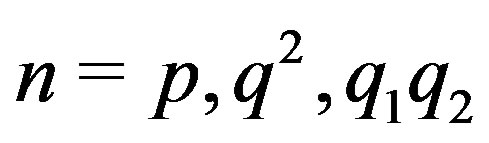 .
.
Observe that, for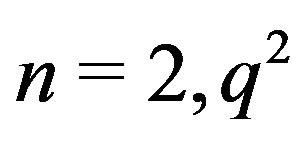 ,
, 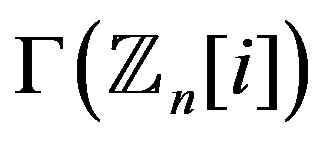 is the empty graph.
is the empty graph.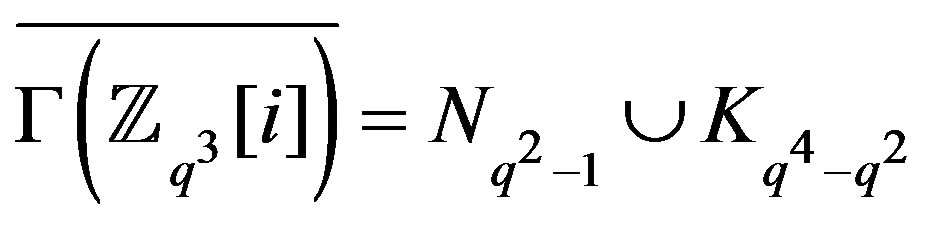 , so the line graph
, so the line graph
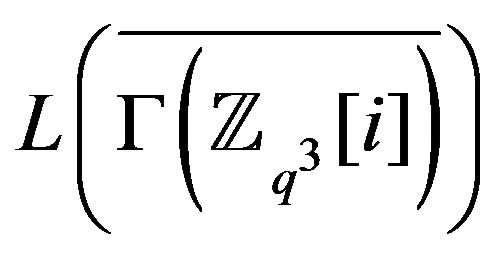 is regular. While
is regular. While 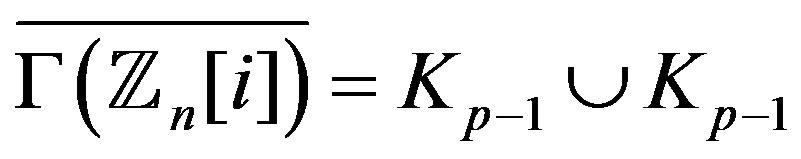
which is regular, so is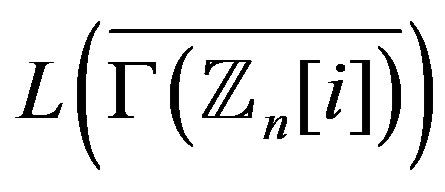 .
.
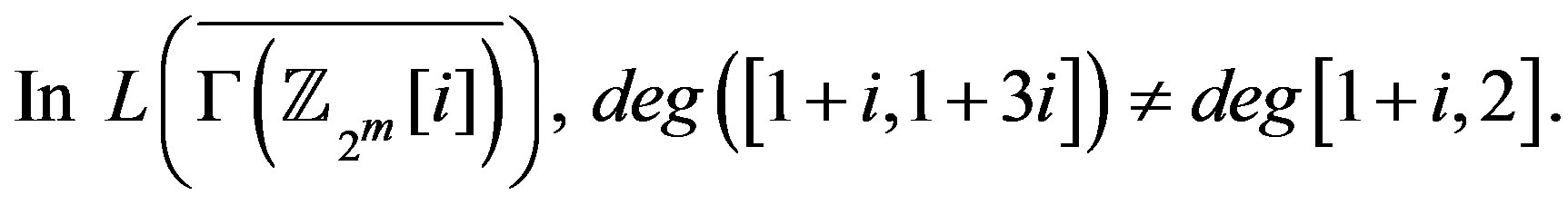
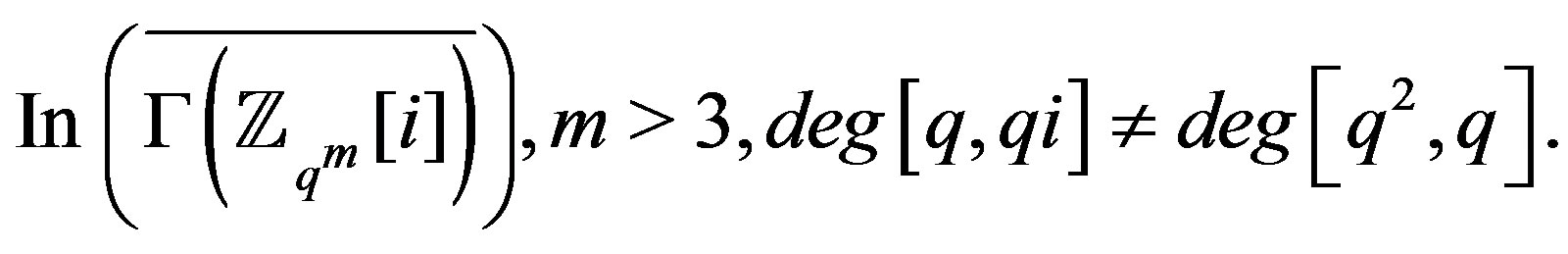
And in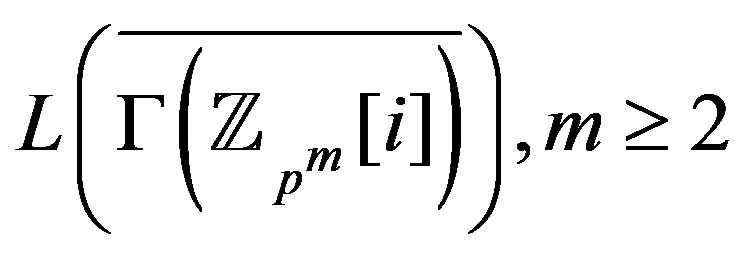 ,
,
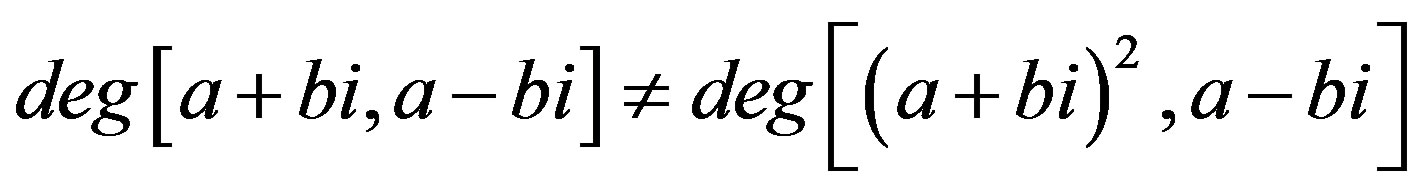 . So, the graph
. So, the graph
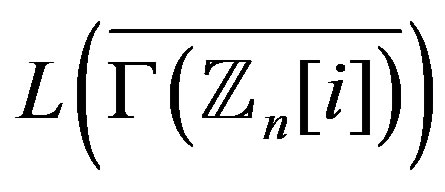 is not regular for
is not regular for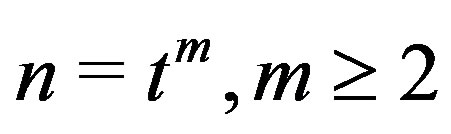 ,
, 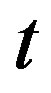 is a prime and
is a prime and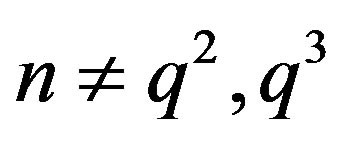 .
.
Theorem 11.5 Let 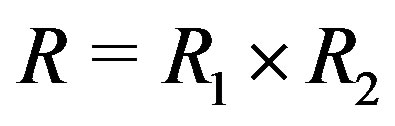 where
where 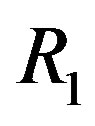 and
and 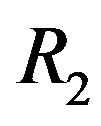 are commutative rings with unity such that
are commutative rings with unity such that
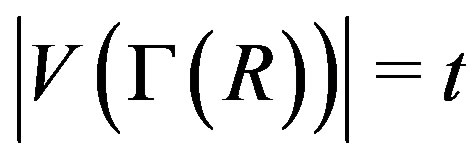 ,
, 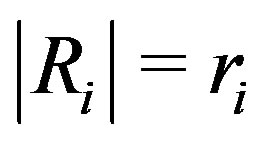 for
for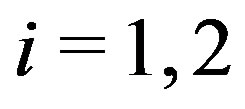 . If
. If 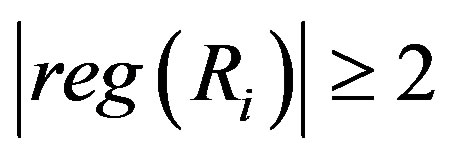
and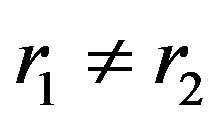 , then
, then 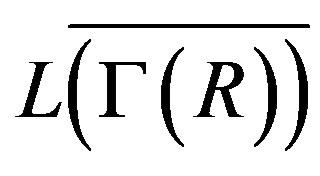 is not regular.
is not regular.
Proof. Since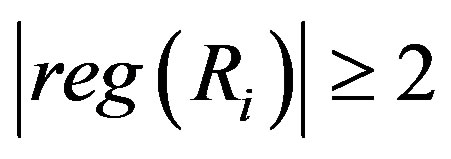 , for
, for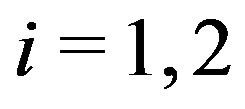 , there exist
, there exist 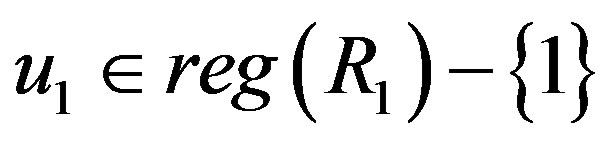 and
and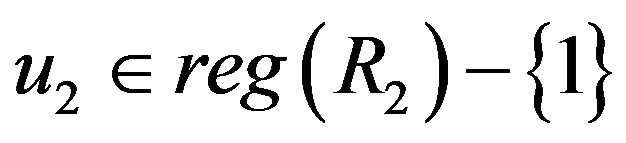 . Therefore
. Therefore
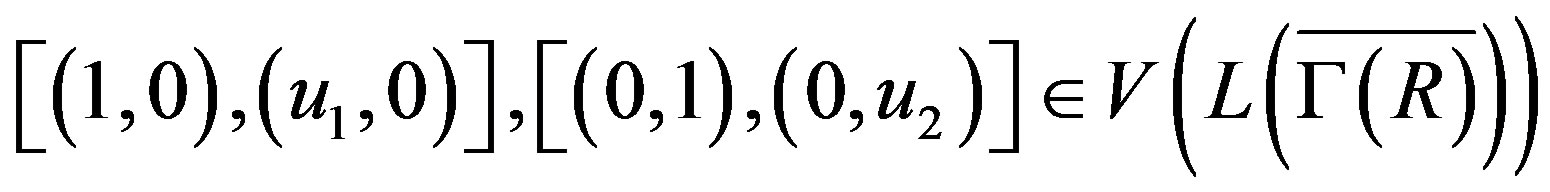 . Since
. Since
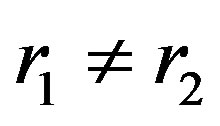 ,
,
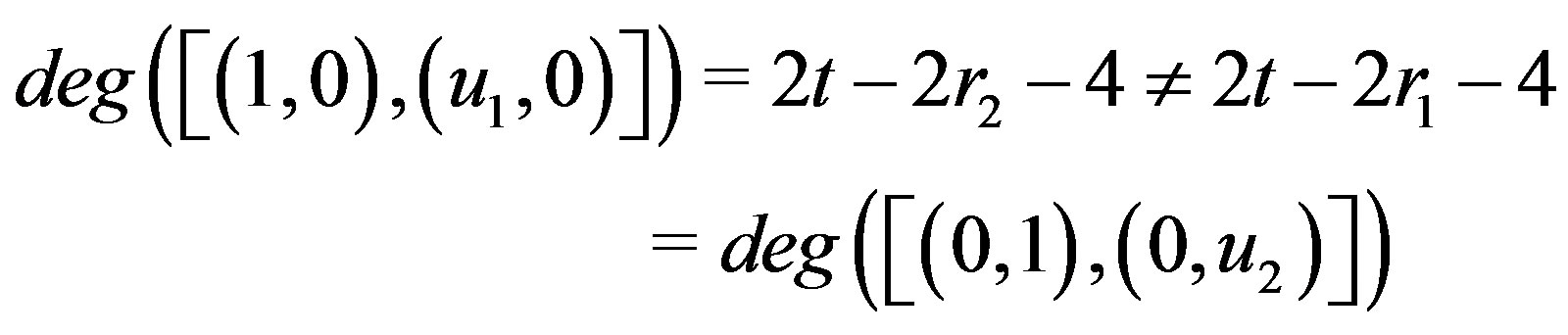 .
.
So, 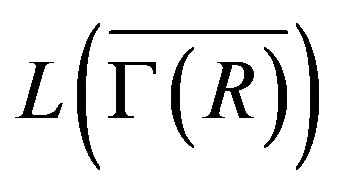 is not regular.
is not regular. 
Theorem 11.6 The graph 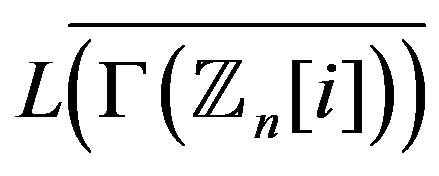 is regular if and only if
is regular if and only if 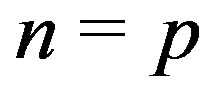 or
or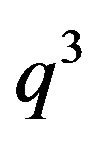 .
.
12. When is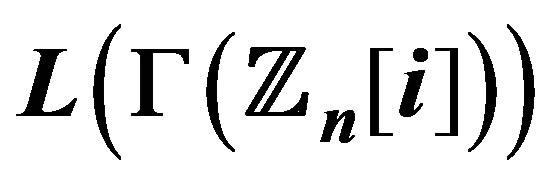 ,
, 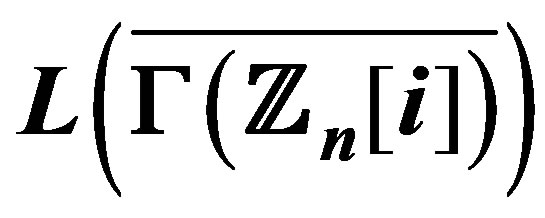 Locally H?
Locally H?
A simple graph 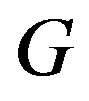 is said to be locally
is said to be locally  if the neighborhood of each vertex in
if the neighborhood of each vertex in 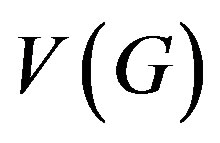 induces the same graph
induces the same graph . The cartesian product
. The cartesian product 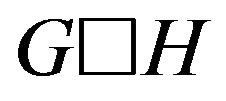 of two graphs
of two graphs 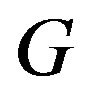 and
and  is the graph with vertex set
is the graph with vertex set 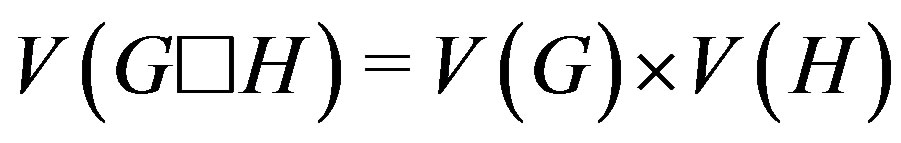 and two vertices in
and two vertices in
 are adjacent if and only if they are equal in one coordinate and adjacent in the other. Before we proceed, we give the following lemma.
are adjacent if and only if they are equal in one coordinate and adjacent in the other. Before we proceed, we give the following lemma.
Lemma 12.1 1) If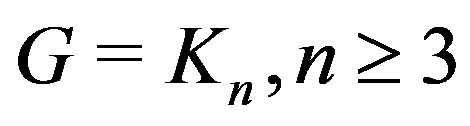 , then
, then 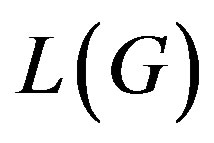 is locally
is locally 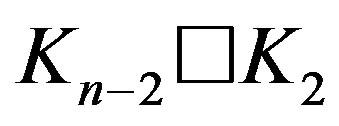 .
.
2) If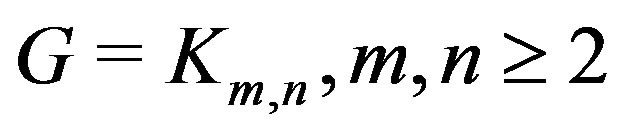 , then
, then 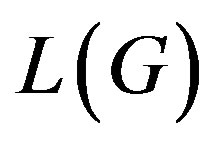 is locally
is locally 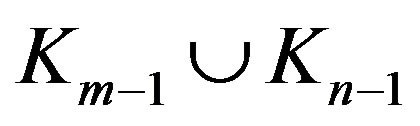 .
.
Proof. 1) Let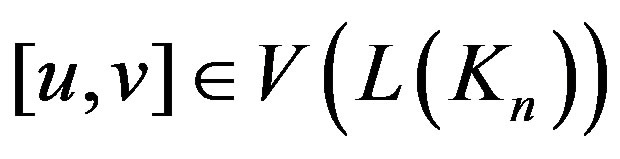 , then
, then
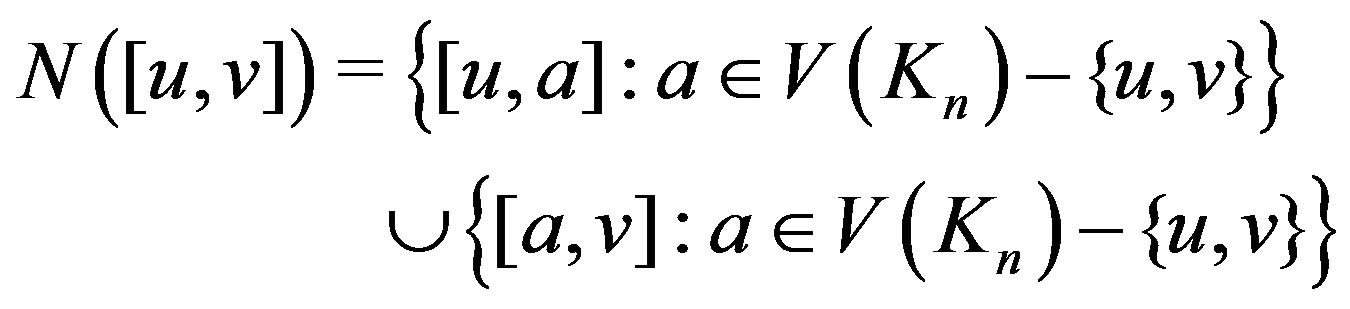
each of the sets 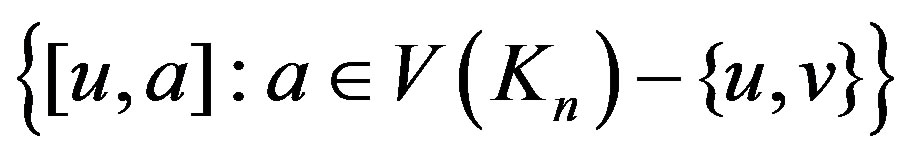 and
and
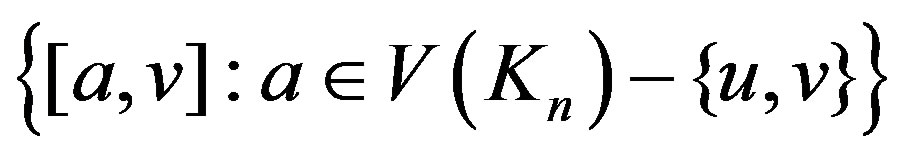 induces a copy of
induces a copy of 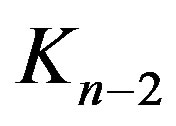 and since we deal with an undirected graphs, then for a fixed
and since we deal with an undirected graphs, then for a fixed ,
, 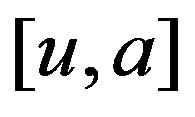 and
and 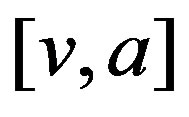 are adjacent. Thus the result holds.
are adjacent. Thus the result holds.
3) Let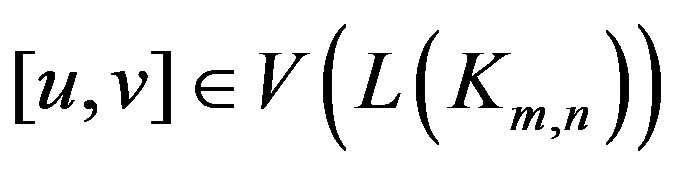 , with partite sets
, with partite sets  and
and 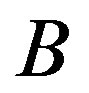 and with
and with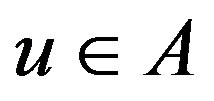 ,
,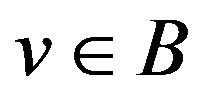 . Then
. Then
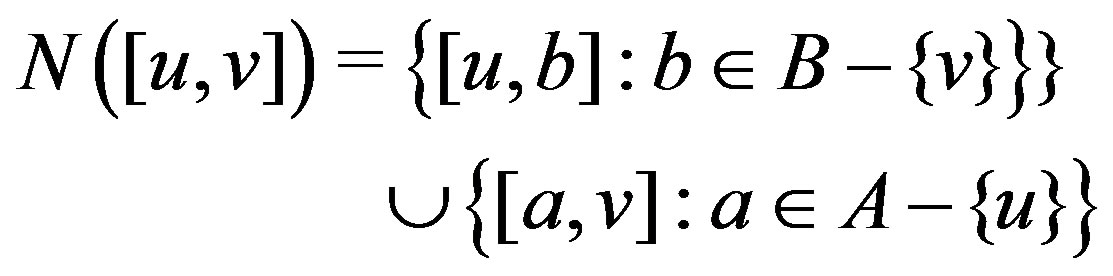 .
.
Each set induces a complete graph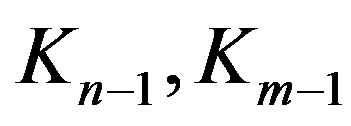 , respectively. And
, respectively. And  has no other edges. Thus
has no other edges. Thus 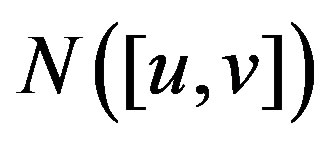 induces
induces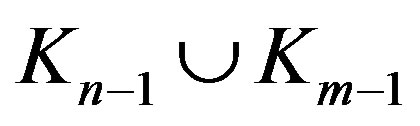 .
. 
In order for a graph to be locally , it should be regular graph. Thus for the graph
, it should be regular graph. Thus for the graph , it suffices to check the cases
, it suffices to check the cases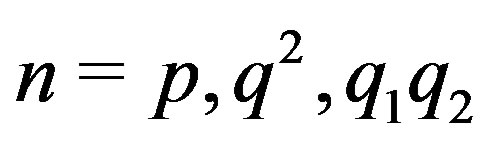 , and for
, and for
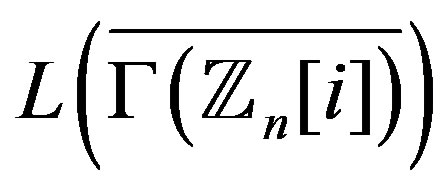 , we consider only the cases
, we consider only the cases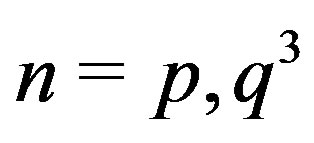 . Since
. Since 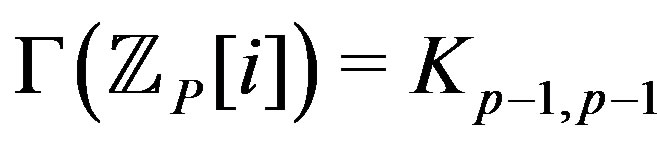 and
and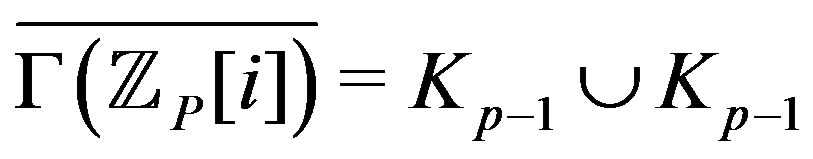 ,
,
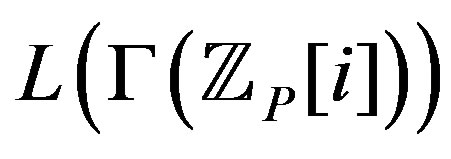 is locally
is locally 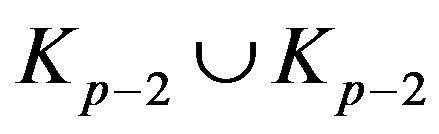 and
and
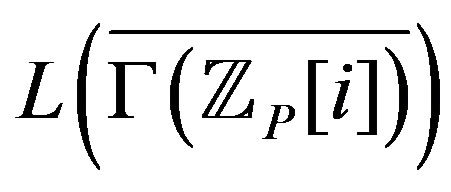 is locally
is locally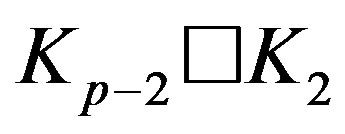 . In the same manner we can show that
. In the same manner we can show that 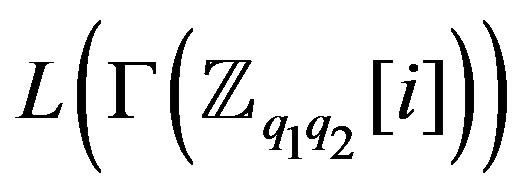 is locally
is locally 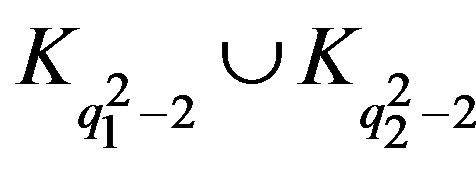 ,
, 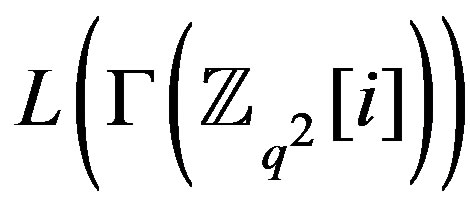 is locally
is locally 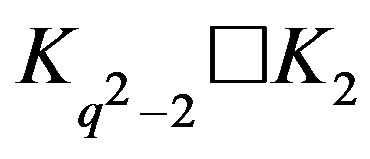 and
and
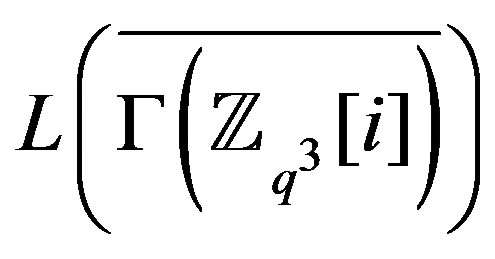 is locally
is locally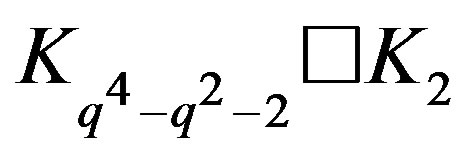 .
.
Theorem 12.2 The following statements are equivalent.
1) The graph 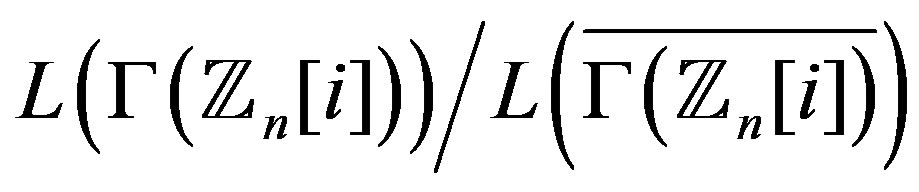 is regular2) The graph
is regular2) The graph 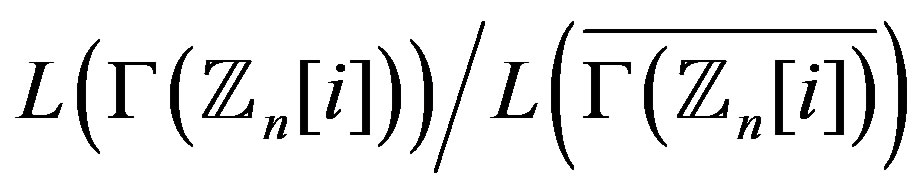 is locally
is locally .
.
REFERENCES
- E. Abu Osba, S. Al-Addasi and N. Abu Jaradeh, “Zero Divisor Graph for the Ring of Gaussian Integers Modulo n,” Communication in Algebra, Vol. 36, No. 10, 2008, pp. 3865-3877. doi:10.1080/00927870802160859
- E. Abu Osba, S. Al-Addasi and B. Al-Khamaiseh, “Some Properties of the Zero Divisor Graph for the Ring of Gaussian Integers Modulo n,” Glasgow Journal of Math, Vol. 53, No. 1, 2011, pp. 391-399. doi:10.1017/S0017089511000024
- E. Abu Osba, “The Complement Graph for Gaussian Integers Modulo n,” Communication in Algebra, accepted.
- K. Nazzal and M. Ghanem, “On the Line Graph of the Zero Divisor Graph for the Ring of Gaussian Integers Modulo n,” International Journal of Combinatorics, Vol. 2012, Article ID 957284. doi:10.1155/2012/957284
- P. F. Lee, “Line Graph of Zero Divisor Graph in Commutative Rings,” Master’s Thesis, Colorado Christian University, 2007.
- J. Sedlàĉek, “Some Properties of Interchange Graphs, Theory of Graphs and Its Applications,” Academic Press, New York, 1962, pp. 145-150.
- G. Dersden and W. M. Dymcek, “Finding Factors of Factor Rings over the Gaussian Integers,” American Mathematical Monthly, Vol. 112, No. 7, 2005, pp. 602- 611. doi:10.2307/30037545
- V. G. Vising, “The Number of Edges in a Graph of a Given Radius,” Soviet Mathematics—Doklady, Vol. 8, 1967, pp. 535-536.
- C. Berg, “Graphs and Hypergraphs,” American Elsevier Publishing Co, Inc., New York, 1976.
- H. J. Veldman, “A Result on Hamiltonian Line Graphs Involving Restrictions on Induced Subgraphs,” Journal of Graph Theory, Vol. 12, No. 3, 1988, pp. 413-420. doi:10.1002/jgt.3190120312
- D. J. Oberly and D. P. Sumner, “Every Connected, Locally Connected Nontrivial Graph with No Induced Claw Is Hamiltonian,” Journal Graph Theory, Vol. 3, No. 4, 1979, pp. 351-356. doi:10.1002/jgt.3190030405
- M. J. Plantholt, “The Chromatic Index of Graphs with Large Maximum Degree,” Discrete Mathematics, Vol. 47, 1983, pp.91-96. doi:10.1016/0012-365X(83)90074-2
- B.-L. Chen and H.-L. Fu, “Total Chromatic Number and Chromatic Index of Split Graphs,” The Journal of Combinatorial Mathematics and Combinatorial Computing, Vol. 17, 1995, pp. 137-146.
- S. Akbari and A. Mohamamadaian, “On the Zero Divisor Graph of a Commutative Ring,” Journal of Algebra, Vol. 274, No. 2, 2004, pp. 847-855. doi:10.1016/S0021-8693(03)00435-6
- S. Arumugam and S. Velammal, “Edge Domination in Graphs,” Taiwanese Journal of Mathematics, Vol. 2, No. 2, 1998, pp. 173-179.

