Open Journal of Discrete Mathematics
Vol.1 No.2(2011), Article ID:5742,4 pages DOI:10.4236/ojdm.2011.12010
b-Chromatic Number of 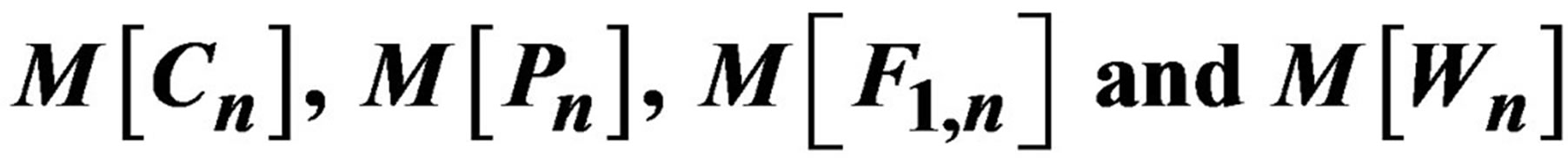
1Department of Maths CA, Kongunadu Arts & Science College, Coimbatore, India
2Department of Mathematics, Kongunadu Arts & Science College, Coimbatore, India
3Department of Mathematics, Indus College of Engineering, Coimbatore, India
E-mail: vijikasc@gmail.com, ktmaths@yahoo.com, roopeshsha@gmail.com
Received April 2, 2011; revised May 2, 2011; accepted May 15, 2011
Keywords: chromatic number, b-chromatic, b-colouring, Middle graph
Abstract
In this paper, we discuss about the b-colouring and b-chromatic number for middle graph of Cycle, Path, Fan graph and Wheel graph denoted as .
.
1. Introduction
Let G be a finite undirected graph with no loops and multiple edges. A coloring (i.e., proper coloring) of a graph G = (V,E) is an assignment of colors to the vertices of G, such that any two adjacent vertices have different colors. A coloring is called a b-coloring [1], if for each color i there exists a vertex xi of color i such that every color j ≠ i, there exists a vertex yj of color j adjacent to xi, such a vertex xi is called a dominating vertex for the colour class i or color dominating vertex which is known as b-chromatic vertex.
The b-chromatic number of a graph G, denoted by j(G) is the largest positive integer k such that G has a b-colouring by k colors. The b-chromatic number of a graph was introduced by R.W. Irwing and manlove [2] in the year 1999 by considering proper colorings that are minimal with respect to a partial order defined on the set of all partitions of V(G). They proved that determining j(G)[3] is NP-hard for general graphs, but polynomial for trees.
Let G be a graph with vertex set V(G) and the edge set E(G). The middle graph [4,5] of G, denoted by M(G) is defined as follows. The vertex set of M(G) is defined as follows. The vertex set of M(G) is V(G) È E(G). Two vertices x, y in the vertex set of M(G) are adjacent in M(G) in case one of the following holds;
1) x, y are in E(G) and x, y are adjacent in G
2) x is in V(G), y is in E(G), and x, y are incident in G.
2. b-Chromatic Number of Middle Graph of Cycle
2.1. Definition of Cycle
A Cycle is a circuit in which no vertex except the first (which is also the last) appears more than once. A cycle with n vertices is denoted by Cn.
2.2. Theorem
For any n ≥ 3, j[M(Cn)] = n.
Proof
Let Cn be a cycle of length n with the vertices V1, V2,  , Vn. By the definition of middle graph the edge Vij for 1 ≤ i ≤ n, 1 ≤ j ≤ n of the cycle Cn is subdivided by the vertex
, Vn. By the definition of middle graph the edge Vij for 1 ≤ i ≤ n, 1 ≤ j ≤ n of the cycle Cn is subdivided by the vertex 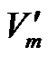 for m = 1, 2,
for m = 1, 2, , n. Here the vertices
, n. Here the vertices , Vi induces a clique of order n.
, Vi induces a clique of order n.
Now assign a proper colouring to these vertices as follows. Consider a colour class C = {c1, c2, c3, , cn}. Assign the color ci to the vertex
, cn}. Assign the color ci to the vertex 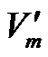 for i = 1, 2,
for i = 1, 2, , n. Here M(Cn) contains a clique of order n, so for proper colouring we require maximum n colours to colour the vertices of
, n. Here M(Cn) contains a clique of order n, so for proper colouring we require maximum n colours to colour the vertices of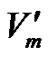 , which produces a b-chromatic coloring. Next we assign a colouring to the vertices Vi for i = 1, 2,
, which produces a b-chromatic coloring. Next we assign a colouring to the vertices Vi for i = 1, 2,  , n. Suppose if we assign any new colour cn+1 to the vertex Vi
, n. Suppose if we assign any new colour cn+1 to the vertex Vi  i = 1, 2,
i = 1, 2, , n, it will not produce a b-chromatic colouring because none of the vertices vi does not realizes its own colours. Therefore the only possibility is to assign an existing colors to the vertices vi.
, n, it will not produce a b-chromatic colouring because none of the vertices vi does not realizes its own colours. Therefore the only possibility is to assign an existing colors to the vertices vi.
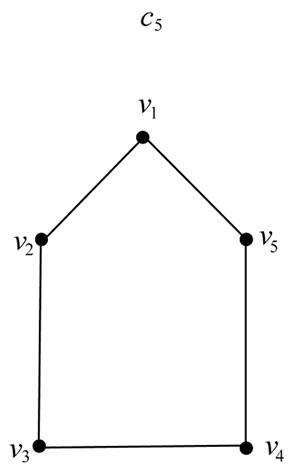 (a)
(a)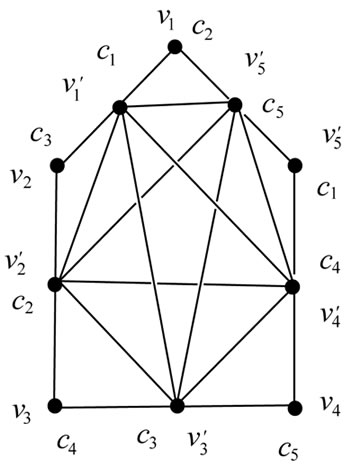 (b)
(b)
Figure 1. (a) [C5]; (b) j{M(C5)} = 5.
Hence by colouring procedure the above said colouring is maximal and b-chromatic.

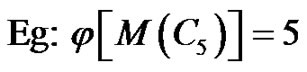
3. b-Chromatic Number of Middle Graph of Path
3.1. Definition of Path
A Path is a sequence of consecutive edges in a graph and the length of the path is the number of edges traversed. A path with n vertices is denoted as Pn.
3.2. Theorem
For any n ≥ 2, 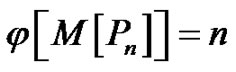
Proof
Let Pn be any path of length n – 1 with vertices v1, v2,  , vn. By the definition of middle graph each edge of vij for 1 ≤ i ≤ n, 1 ≤ j ≤ n of the path graph Pn is subdivided by the vertex
, vn. By the definition of middle graph each edge of vij for 1 ≤ i ≤ n, 1 ≤ j ≤ n of the path graph Pn is subdivided by the vertex 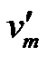 in M[Pn] and the vertices
in M[Pn] and the vertices 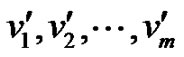 along with
along with 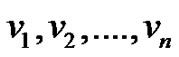 induces a clique of order n in M[Pn].
induces a clique of order n in M[Pn].
i.e., 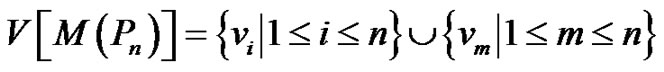
Now consider a proper colouring to M[Pn] as follows. Consider the colour class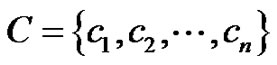 . Assign the color ci to the vertices
. Assign the color ci to the vertices 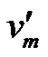 for i = 1, 2,
for i = 1, 2,  , n. Here M[Pn] contains a clique of order n. So for proper colouring it require n distinct colours which results in b-chromatic coloring. Next we assign the coloring to the vertices vi for i = 1, 2,
, n. Here M[Pn] contains a clique of order n. So for proper colouring it require n distinct colours which results in b-chromatic coloring. Next we assign the coloring to the vertices vi for i = 1, 2, , n. Suppose if we assign the colour cn+1 to the vertex vi
, n. Suppose if we assign the colour cn+1 to the vertex vi  i =
i = n which does not produces b-coloring. Hence we should assign only an existing colours to the vertices
n which does not produces b-coloring. Hence we should assign only an existing colours to the vertices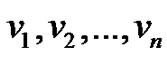 . Hence by coloring procedure it is the maximal and b-chromatic coloring.
. Hence by coloring procedure it is the maximal and b-chromatic coloring.
 (a)
(a) (b)
(b)
Figure 2. (a) P3; (b) j[M(P3)] = 3.
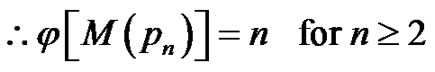 .
.

4. b-Chromatic Number of Midlle Graph of Fan Graph
4.1. Definition of Fan Graph
A fan graph Fm,n is defined as the graph join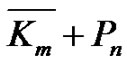 , where
, where  is the empty graph on nodes and
is the empty graph on nodes and 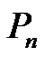 is the path on n nodes.
is the path on n nodes.
4.2. Theorem
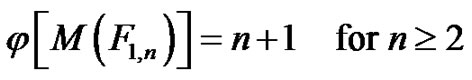
Proof
Let (x,y) be the bipartition of Fm,n with |x| = m and |y| = n. Let V be the only vertex of x and y = {v, v2,  , vn}. By the definition of Middle graph each edge vvi for i = 1, 2, 3,
, vn}. By the definition of Middle graph each edge vvi for i = 1, 2, 3,  , n of F1,n is subdivided by the vertex
, n of F1,n is subdivided by the vertex 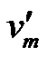 in M[F1,n] and the vertices
in M[F1,n] and the vertices , v induces a clique of order n + 1 in M[F1,n].
, v induces a clique of order n + 1 in M[F1,n].
i.e.,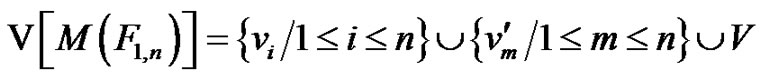 .
.
Now assign a proper colouring to these vertices as follows. Consider a colour class C = {c1, c2, , cn+1}. First assign the colour c1, c2,
, cn+1}. First assign the colour c1, c2, , cn to the vertices
, cn to the vertices 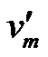 for m = 1, 2,
for m = 1, 2, , n. Here M[F1,n] contains a clique of order n. So for proper colouring we require n distinct colours which results as b-chromatic colouring. Next assign the colour
, n. Here M[F1,n] contains a clique of order n. So for proper colouring we require n distinct colours which results as b-chromatic colouring. Next assign the colour 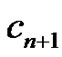 to the vertex v and
to the vertex v and  to the vertices
to the vertices . Here the vertex v realizes its own colors but the vertices
. Here the vertex v realizes its own colors but the vertices 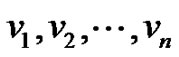 does not realizes its own colors, so we cannot assign any new colours to the vertices
does not realizes its own colors, so we cannot assign any new colours to the vertices 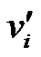 for i = 1, 2,
for i = 1, 2, , n. Therefore by assigning only existing colors to the vi produces a b-chromatic coloring. Hence by coloring procedure the above said col-
, n. Therefore by assigning only existing colors to the vi produces a b-chromatic coloring. Hence by coloring procedure the above said col-
 (a)
(a)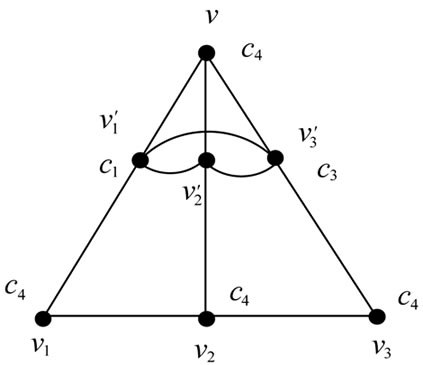 (b)
(b)
Figure 3. (a) [F1,3]; (b) j[M(F1,3)] = 4.
oring is maximal.
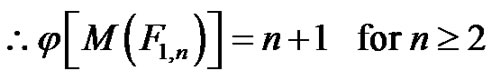 .
.

5. b-Chromatic Number of Middle Graph of Wheel Graph
5.1. Definition of Wheel Graph
A graph Wn of order n which contains a cycle of order n − 1, and for which every graph vertex in the cycle is connected to one other graph vertex (which is known as hub). The edges of a wheel which include the hub are spokes.
5.2. Theorem
For any n > 4, j[M(Wn)] = n
Proof
Let 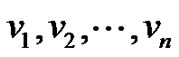 be the vertices taken in anticlock wise direction in the wheel graph wn, where vn is the hub. In M(wn), by the definition of middle graph the edge incident with vi together with vertex vi induces a clique of n vertices in M(wn). Let
be the vertices taken in anticlock wise direction in the wheel graph wn, where vn is the hub. In M(wn), by the definition of middle graph the edge incident with vi together with vertex vi induces a clique of n vertices in M(wn). Let 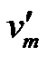 be the clique in M(wn) for i = 1, 2,
be the clique in M(wn) for i = 1, 2, , n.
, n.
Now consider a proper colouring to these vertices as follows. Consider the color class . First assign the color
. First assign the color 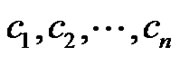 to the vertex
to the vertex 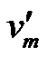 for i = 1, 2,
for i = 1, 2, , n. By the above statement that M(wn) contains a clique of order n, so we need only n colors to colour the vertices. Next we assign the color cn+1 to the hub. Here the vertices
, n. By the above statement that M(wn) contains a clique of order n, so we need only n colors to colour the vertices. Next we assign the color cn+1 to the hub. Here the vertices 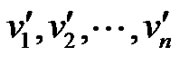 and the hub vn realizes its colors, which produces a b-chromatic coloring. Next if we assign any new color to the vertices vi for i = 1, 2,
and the hub vn realizes its colors, which produces a b-chromatic coloring. Next if we assign any new color to the vertices vi for i = 1, 2, , n − 1, it will not produce a b-chromatic coloring. So we should assign the existing colors cn+1 to the vertices vi for i = 1, 2,
, n − 1, it will not produce a b-chromatic coloring. So we should assign the existing colors cn+1 to the vertices vi for i = 1, 2, , n−2 and c1 to the verter vn−1. Hence by coloring procedure it is the maximum and b-chromatic coloring.
, n−2 and c1 to the verter vn−1. Hence by coloring procedure it is the maximum and b-chromatic coloring.
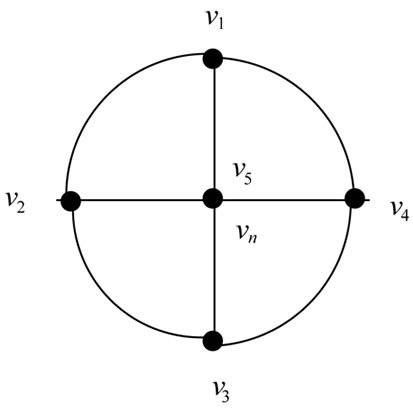 (a)
(a)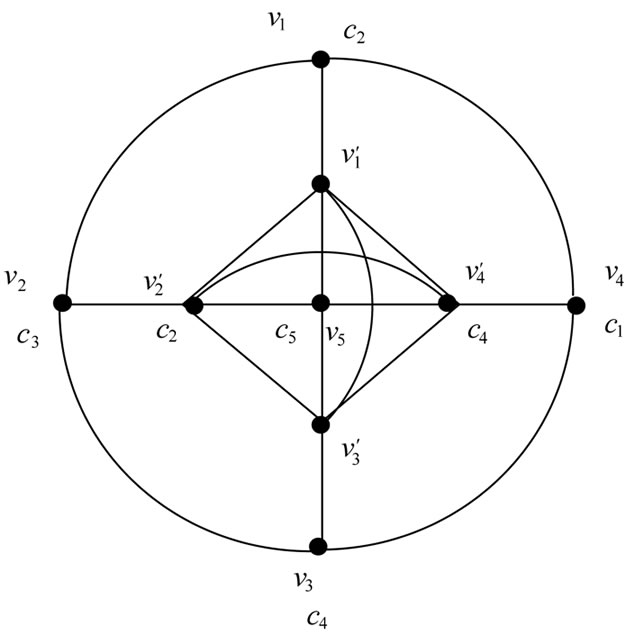 (b)
(b)
Figure 4. (a) [w5]; (b) j[M(w5)] = 5.

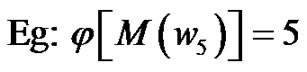
6. References
[1] S. Corteel, M. Valencia-Pabon and J.-C. Vera, “On Aproximating the b-chromatic Number,” Discrete Applied Mathematics, Vol. 146, No. 1, 2005, pp. 106-110. doi:10.1016/j.dam.2004.09.006
[2] R. W. Irving and D. F. Manlove, “The b-chromatic Number of a Graph,” Discrete Applied Mathematics, Vol. 91, No. 1, 1999, pp. 127-141. doi:10.1016/S0166-218X(98)00146-2
[3] M. Kouider, “b-chromatic Number of a Graph,” Subgraphs and Degrees Rappor interne LRI 1392.
[4] V. J. Vernold, M. Venkatachalam and A. M. M. Akbar “A Note on Achromatic Coloring of Star Graph Families,” Filomat, Vol. 23, No. 3, 2009, pp. 251-255. doi:10.2298/FIL0903251V
[5] K. Thilagavathi and N. Roopesh, “Generalization of Achromatic Colouring of Central Graphs,” Electronic Notes in Discrete Mathematics, Vol. 33, 2009, pp. 147-152. doi:10.1016/j.endm.2009.03.021
[6] V. J. Vernold and A. M.M. Akbar, “On Harmonious Coloring of Middle Graph of C(Cn),C(K1,n) and C(Pn),” Note di Matematica, Vol. 29, No. 2, 2009, pp. 201-211.
[7] H. Hajiabolhassan, “On the b-chromatic Number of Kneser Graphs,” Discrete Applied Mathematics, Vol. 158, No. 3, 2010, pp. 232-234. doi:10.1016/j.dam.2009.09.023
[8] B. Effantin, “The b-chromatic Number of power Graphs of Complete Caterpillars,” The Journal of Discrete Mathematical Sciences & Cryptography, Vol. 8, 2005, pp. 483-502.
[9] C. T. Hoang and M. Kouider, “On the B-Dominating Colouring of Graphs,” Discrete Applied Mathematics, Vol. 152, No.1-3, 2005, pp. 176-186. doi:10.1016/j.dam.2005.04.001

