Optics and Photonics Journal
Vol.3 No.2(2013), Article ID:32728,9 pages DOI:10.4236/opj.2013.32028
An Exact Analysis of the Fundamental and First Higher Order Mode in Graded Index Fibers with Direct Power Series Method
1Department of Physics, Kanksa Academy of Technology & Management, Kanksa, India
2Department of Physics, Banwarilal Bhalotia College, Asansol, India
Email: research_phy@rediffmail.com, dkbbcasn@gmail.com
Copyright © 2013 Anirban Roy Chowdhury et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 17, 2013; revised March 20, 2013, accepted March 28, 2013
Keywords: Power Series Method; Chebyshev Series Method; Petermann-2 Spot Size; Cut-Off Frequency
ABSTRACT
An exact and fast analytic method based on power series is established to predict the modal field distributions, Petermann-2 spot size, the normalized propagation constant corresponding to fundamental and first higher order mode in graded index fibers with any arbitrary power law profile. The variation of normalized cut-off frequencies of some LPlm modes in graded index fibers with different profile exponents are also shown here and an empirical relation between them is determined.
1. Introduction
First few modes of graded index fiber find some important applications in the field of optical communication in recent times. LP11 mode was used to design fiber sensors to separate temperature variation from longitudinal strain by intermodal interference [1]. Optical fiber mode filters in dual mode transmission system have also been developed using LP01-LP11 modes [2]. As a wavelength filter, the LP01-LP11 mode coupler offers much narrower spectral width than a coupler whose constituent fibers are single-mode. This coupler may also be used as a mode converter for dispersion compensation application [3]. The transmission characteristics of dual mode and dual polarization of CO-OFDM system are studied using LP01- LP11 mode [4,5]. In recent times, there is considerable effort on developing few mode fibers to enhance the system capacity based on mode division multiplexing and multiple-input multiple-output digital signal processing [6-8].
Earlier, graded index fibers were analyzed numerically with beam propagation method [9], finite difference method [10], matrix methods [11] etc. to study their modal properties and various propagation characteristics. Beam propagation method, finite difference, finite element methods involve complex algorithms; moreover, these are inaccurate as one approaches cut-off region.
Matrix methods are problematic for profiles with sharp index difference. In the literature, there are some approximate analytic methods also like variational analysis [12,13], Chebyshev power series method [14,15] etc. The analytic methods involve cumbersome algebraic calculations followed by some computation; due to approximations these methods are not so accurate. There are some works based on direct power series method [16,17] solution but those were confined to the fundamental mode only.
In this paper, our approach is to apply the power series method (PSM) in a most general way to solve the wave equation for graded index fiber. For step index fiber (SIF), the modal solutions of Helmholtz equation are Bessel’s functions arising from recursion relations in power series method. We have shown that for graded index fiber also, one can find a simple series solution with the recursion relation slightly modified and the derived series is also convergent. Depending on the power exponent value, one part of the recursion relation is different; the rest is the same as in Bessel function.
We have solved scalar Helmholtz equation governing the power flow in a graded index waveguide by deriving general recursion relations for any mode, any arbitrary profile exponent and developing a simple algorithm. Since the current interest is in Two Mode Fibers where LP01 and LP11 modes both exist, it is important to find the range within which these modes can exist. We have compared our data with one analytic method like Chebyshev Power Series (CPS) technique, as it is already established as an approximate analytic method for the calculation of different propagation characteristics of graded index fiber in LP01 and LP11 mode [14,15]. We found that Chebyshev technique results are in close accordance with our values. It is clear from our results and comparison of computation time with Chebyshev technique, that, PSM is one accurate, fast and simple method for the determination of modal fields and related quantities of a graded index fiber with any arbitrary geometric profile function.
We have studied modal field distributions, Petermann- 2 spot size, normalized propagation constants, cut-off frequencies for LP01-LP11 modes. Earlier works on cut-off frequency calculations based on matrix method [18], perturbation method [19] and variational method [20], are compared with our approach. The calculation of cut-off frequency by PSM shown in this paper proves to be an exact method in comparison to earlier methods.
In Section 2, we have shown the necessary recursion relations while solving the Helmholtz equation with PSM, incorporating the role of the profile exponent. Results are shown in Section 3. In Section 3.1, we have shown the modal field distribution of LP01 and LP11 modes for a particular normalized frequency and also presented the values of Petermann-2 spot size. In Section 3.2, the dependence of normalized propagation constant on normalized frequencies has been illustrated for LP01-LP11 modes. In Section 3.3, we have shown the variation of normalized cut-off frequencies with profile exponent values using PSM. In Section 3.4, we have compared our LP11 mode cut-off frequency data with results existing in literature and in Section 3.5, we have derived a convenient empirical formula relating the above two quantities.
2. Theory
2.1. Modal Solution in an Optical Fiber
In the weakly-guiding approximation, Helmholtz Equation governing light propagation in an optical fiber is [21]
 (1)
(1)
where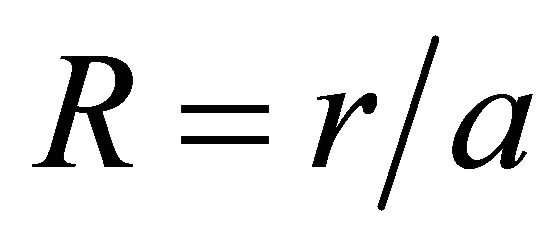 , r is radial co-ordinate, a is core radius;
, r is radial co-ordinate, a is core radius; 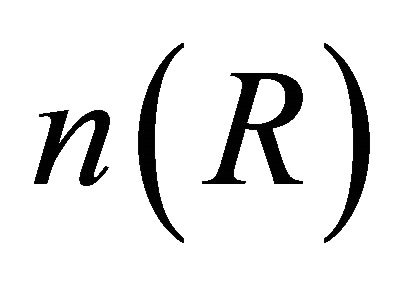 is the refractive index distribution in the fiber;
is the refractive index distribution in the fiber;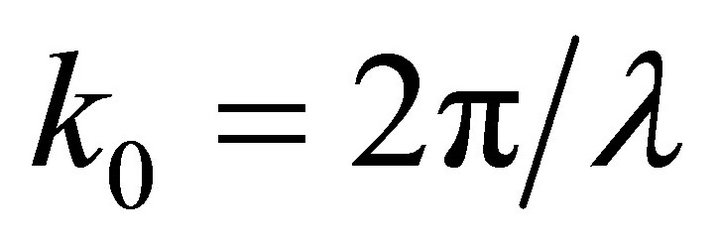 , l is free space wavelength;
, l is free space wavelength;  is the propagation constant; l is a parameter coming from the azimuthal part after separation of variables.
is the propagation constant; l is a parameter coming from the azimuthal part after separation of variables.  is any transverse field component, either E-field or H-field.
is any transverse field component, either E-field or H-field.
In fibers with graded index core, 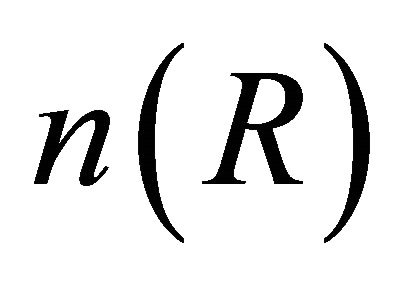 falls from n1—the refractive index value on the axis of the fiber to n2—the refractive index value at the core-cladding interface. Then
falls from n1—the refractive index value on the axis of the fiber to n2—the refractive index value at the core-cladding interface. Then
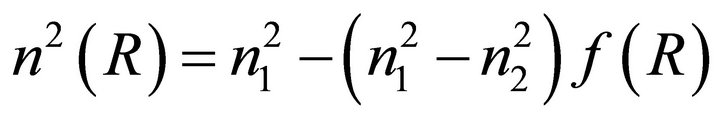 (2)
(2)
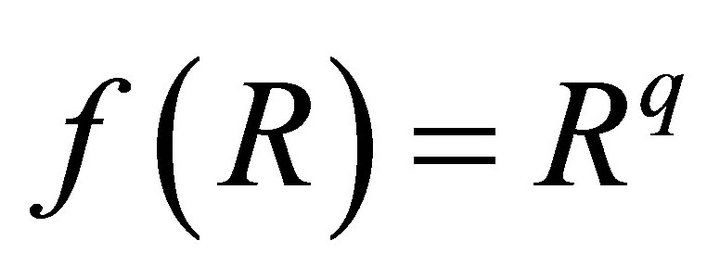 is called profile function. The exponent q in
is called profile function. The exponent q in 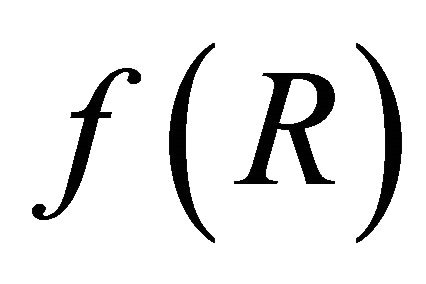 gives the shape of the core index profile. The distribution
gives the shape of the core index profile. The distribution  is called triangular profile;
is called triangular profile; 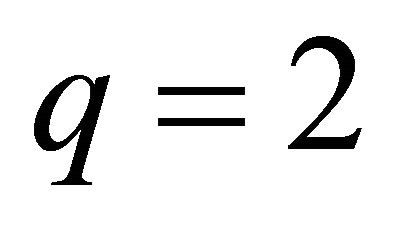 is called parabolic profile.
is called parabolic profile. 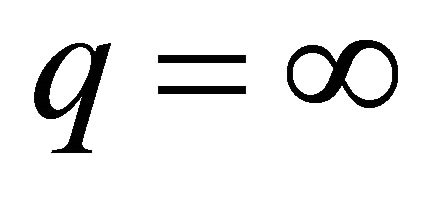 stands for uniform core with index n1; when the cladding index is uniform (having the refractive index value n2) as in our case, it is a step index fiber. The power or exponent q of R setting the profile shape is very important in fibers allowing more than one mode to propagate. It controls numerical aperture, intermodal dispersion, zero dispersion wavelength etc. in multimode fibers.
stands for uniform core with index n1; when the cladding index is uniform (having the refractive index value n2) as in our case, it is a step index fiber. The power or exponent q of R setting the profile shape is very important in fibers allowing more than one mode to propagate. It controls numerical aperture, intermodal dispersion, zero dispersion wavelength etc. in multimode fibers.
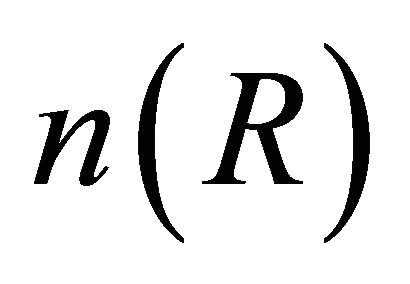 is defined as in (2), (1) becomes
is defined as in (2), (1) becomes
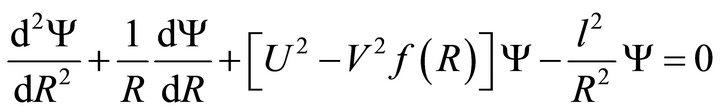 (3)
(3)
where 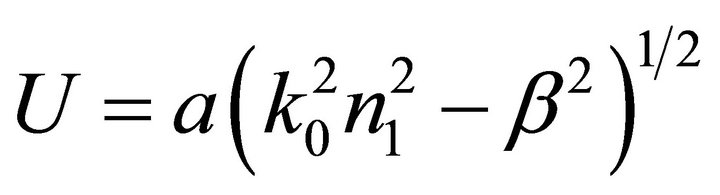 and
and . V is called normalized frequency and U is called normalized propagation constant. Equations (1) or (3) has two linearly independent solutions. For a particular l, the solutions are denoted as LPlm.
. V is called normalized frequency and U is called normalized propagation constant. Equations (1) or (3) has two linearly independent solutions. For a particular l, the solutions are denoted as LPlm.
The mode with highest b is the fundamental mode, denoted as LP01 mode. LP11 is the next higher order mode. Within the core, one has to find the solution of (3) with .
.
Outside the core i.e. in the cladding, ; Equation (3) becomes
; Equation (3) becomes
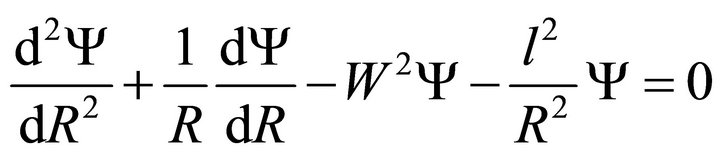 (4)
(4)
where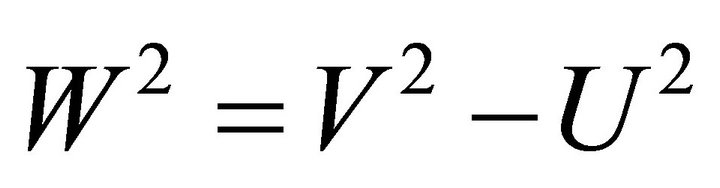 . The solution of (4) is standard modified Bessel function. In region I, that is within the core let the solution be
. The solution of (4) is standard modified Bessel function. In region I, that is within the core let the solution be 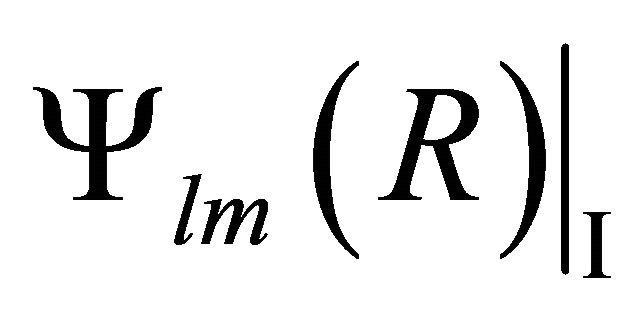 and in region II, that is in the cladding, the solution is
and in region II, that is in the cladding, the solution is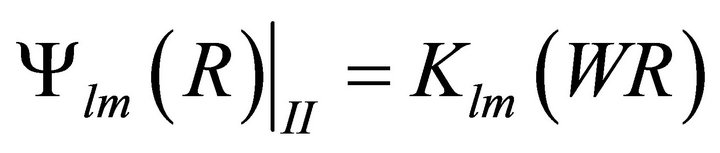 .
.
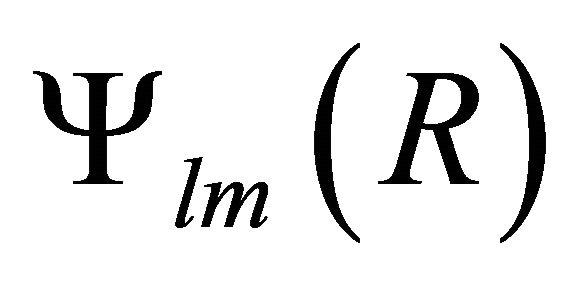 satisfies the following boundary conditions at the interface between region I and region II that is at
satisfies the following boundary conditions at the interface between region I and region II that is at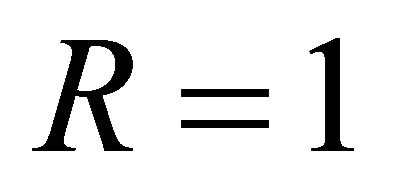 :
:
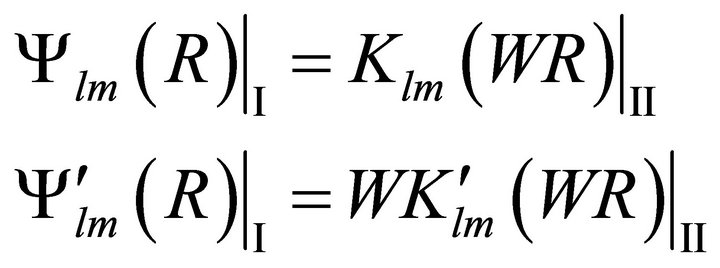 (5)
(5)
2.2. Power Series Method
Using power series technique, 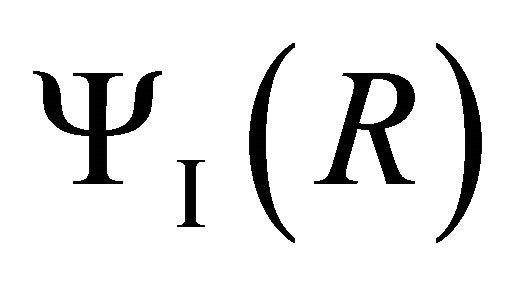 , the solution of (3) in region I, can be expanded in the following form
, the solution of (3) in region I, can be expanded in the following form
 (6)
(6)
As in the solution of Bessel’s Equation, we take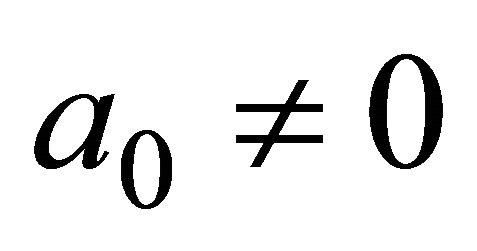 , then
, then 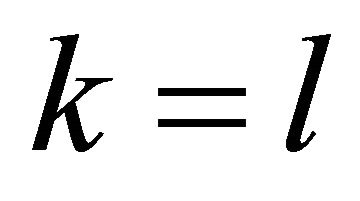 and
and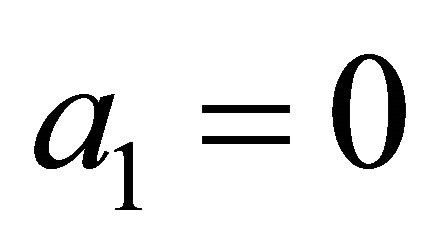 .
.
For any q,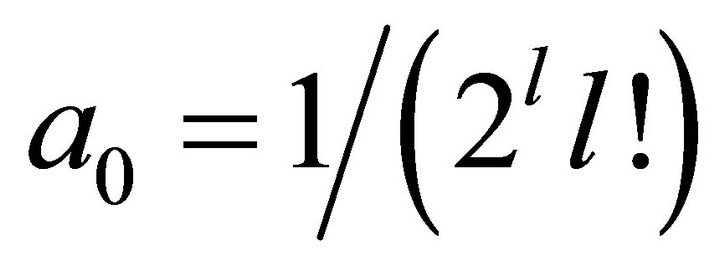 . Here we have used the same normalization factor used in the solution of Bessel’s equation, because for
. Here we have used the same normalization factor used in the solution of Bessel’s equation, because for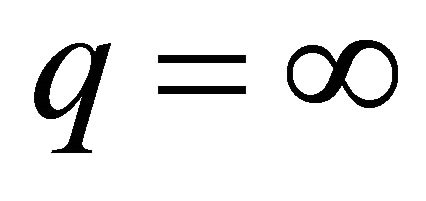 , the series must converge to Bessel function.
, the series must converge to Bessel function.
The recursion relation consists of two parts 1) (7)
(7)
2)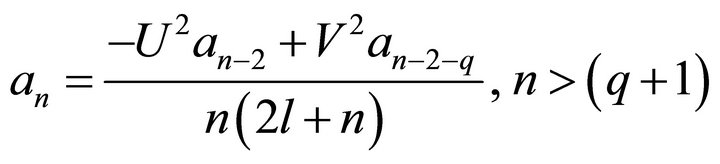 (8)
(8)
where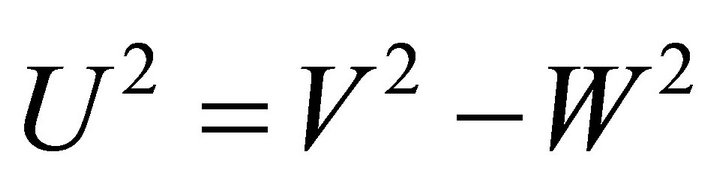 . Evidently, for even q, all the odd coefficients are zero. For odd q, the odd coefficients are zero up to
. Evidently, for even q, all the odd coefficients are zero. For odd q, the odd coefficients are zero up to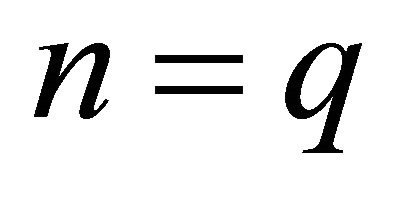 ; all the coefficients are non-zero for
; all the coefficients are non-zero for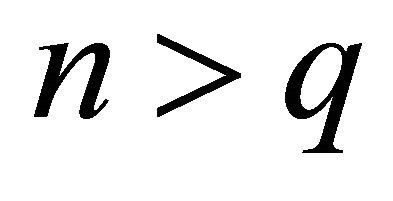 .
.
Using the standard recurrence relation for the modified Bessel function, one gets at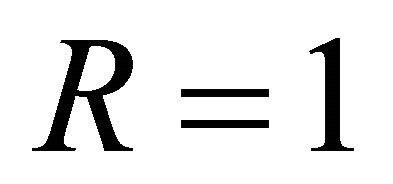 :
:
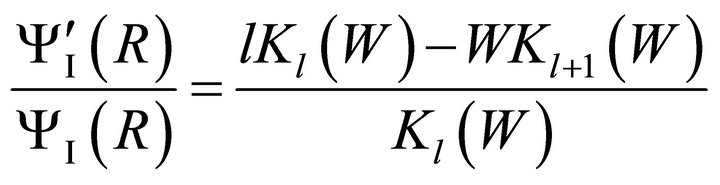 (9a)
(9a)
or
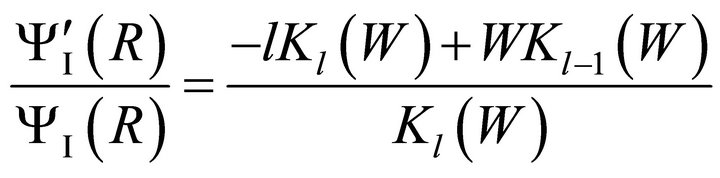 (9b)
(9b)
To find out the value of unknown W, the above equation is to be solved at the interface for a given value of V, starting with an initial value of W. Then the values of all coefficients are known from (7)-(8). Putting these values in (6) we get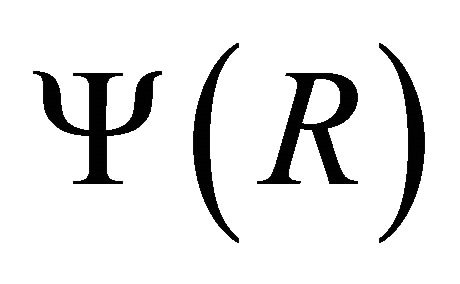 :
:
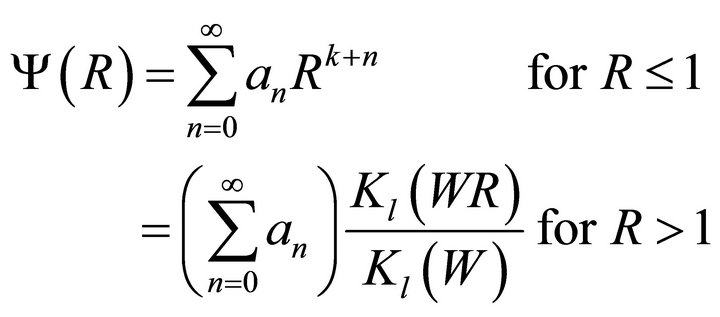 (10)
(10)
The Petermann-2 spot size is given by:
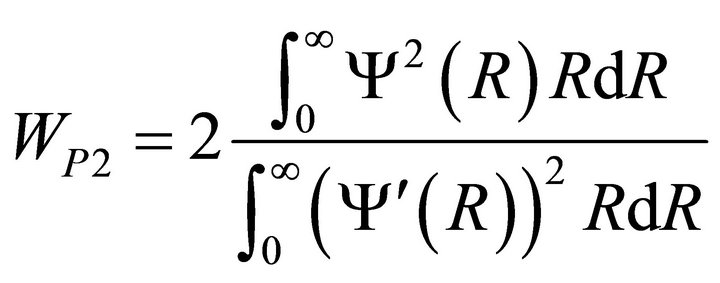 (11)
(11)
The normalized propagation constant is defined as
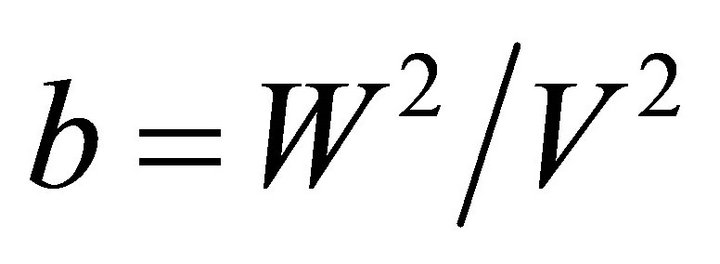 (12)
(12)
The normalized cutoff frequency 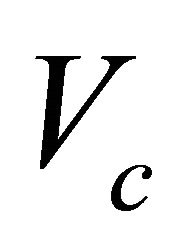 is an important characteristic of a fiber as it demarcates between the range of one mode and its next higher mode. The cut-off condition of a mode is
is an important characteristic of a fiber as it demarcates between the range of one mode and its next higher mode. The cut-off condition of a mode is 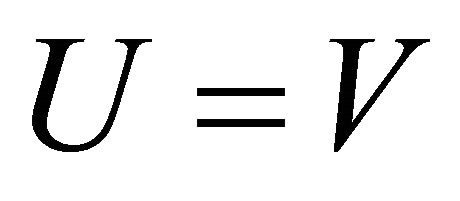 or
or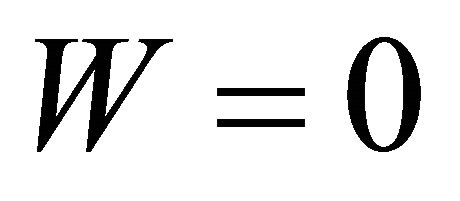 .
.
Applying this condition in (9b) which gives proper limiting values of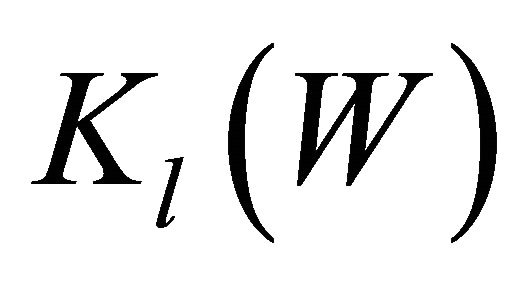 , one obtains
, one obtains
 (13)
(13)
Using this relation, one can get the values of 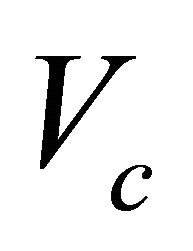 for different q corresponding to different LPlm modes.
for different q corresponding to different LPlm modes.
3. Results and Discussions
Using PSM, we first solved the second order Helmholtz Equation (3) keeping l non-zero so as to get a general solution for any mode and considering different profile exponents both odd and even. Then using this solution we obtained different waveguide parameters like Petermann-2 spot size, normalized propagation constant, normalized cutoff frequency etc.
To find unknown W, we start with an initial value of W for a normalized frequency V and a particular profile exponent q. We evaluate the coefficients from recursion relation (7)-(8); that gives 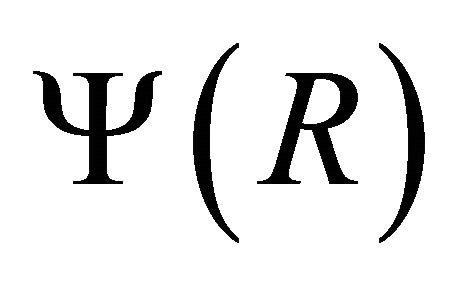 and
and 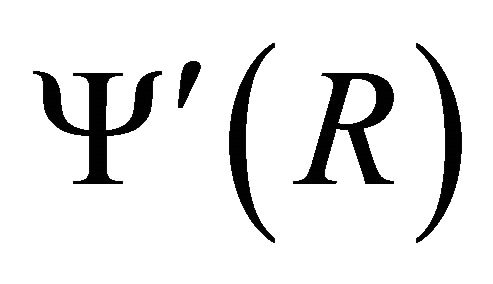 at R = 1. This is matched with
at R = 1. This is matched with  at R = 1. It was observed that 500 terms are sufficient even for q as high as 200. However, we kept about 2000 terms in the series, matching is done with accuracy of the order of 10−8 and the run time is found to be less than a second.
at R = 1. It was observed that 500 terms are sufficient even for q as high as 200. However, we kept about 2000 terms in the series, matching is done with accuracy of the order of 10−8 and the run time is found to be less than a second.
In Section 3.1, we have shown the modal field distributions for LP01-LP11 modes and determined Petermann-2 spot size which is a measure of the spread of the fields around the axis.
In Section 3.2, we have shown the variation of the normalized propagation constant b with normalized frequency V; this gives an idea about the dispersion in the fiber.
To find normalized cut-off frequencies, we evaluate  and
and 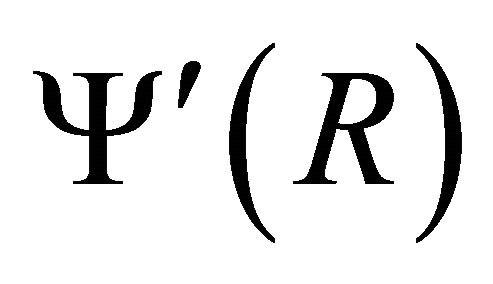 at
at 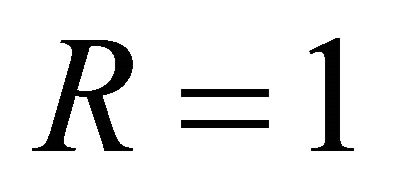 using recursion relations (7)-(8) and putting
using recursion relations (7)-(8) and putting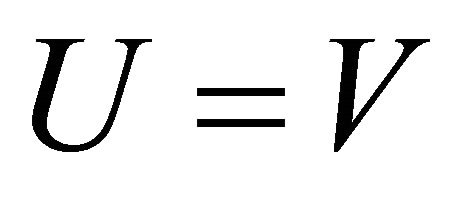 .
.
We have compared our results with those obtained by Chebyshev method already reported in our earlier paper [15]. It was shown there that the values of propagation characteristics of LP11 mode in parabolic and triangular index fibers obtained by CPS technique using four Chebyshev points closely matched with standard numerical values.
In our graphs, following line properties are used for different q values:
Solid red line (–) for PSM with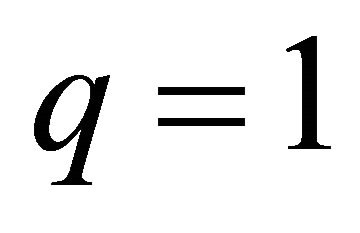 ;
;
Solid blue line (–) for PSM with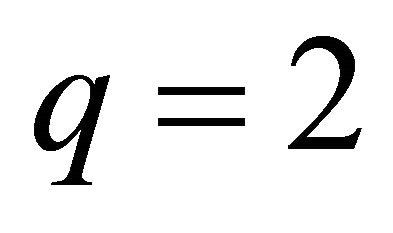 ;
;
Solid green line (–) for PSM with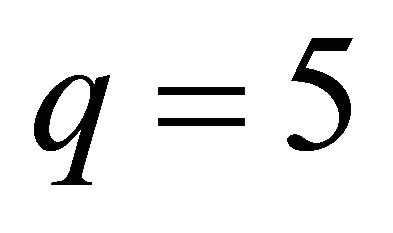 ;
;
Solid magenta line (–) for PSM with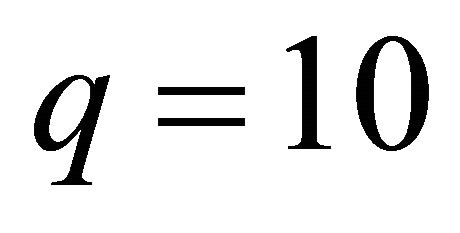 ;
;
Solid black line (–) for PSM with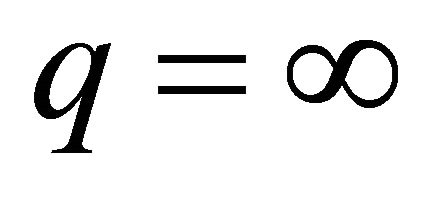 .
.
Dots (·) represent the values obtained by Chebyshev power series method for the corresponding profile (in Figures 1(a) and (b)).
3.1. Modal Field Distributions of LP01 and LP11 Mode
The variations of fundamental and first higher order modal fields for various profile functions with normalized radius are shown in Figures 2(a) and (b).
 (a)
(a)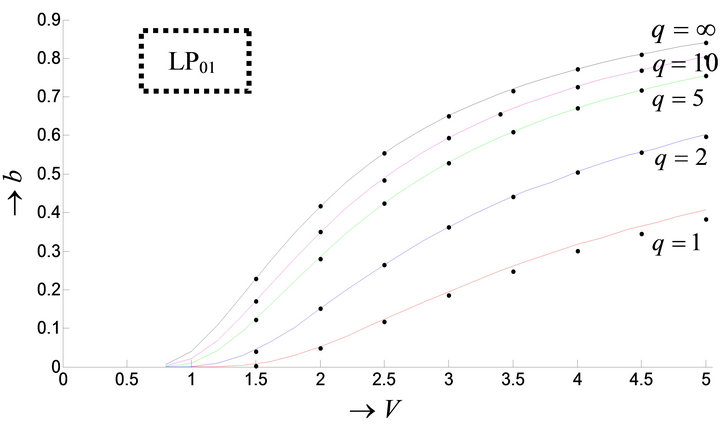 (b)
(b)
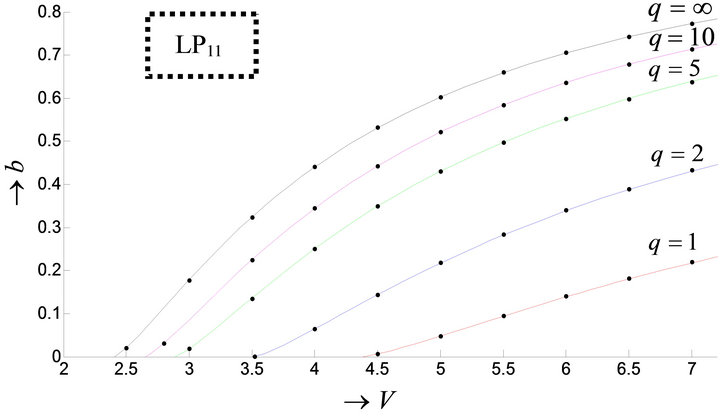
Figure 1. (a) Variation of normalized propagation constant b with normalized frequency V: LP01 mode; (b) Variation of normalized propagation constant b with normalized frequency V: LP11 mode.
 (a)
(a)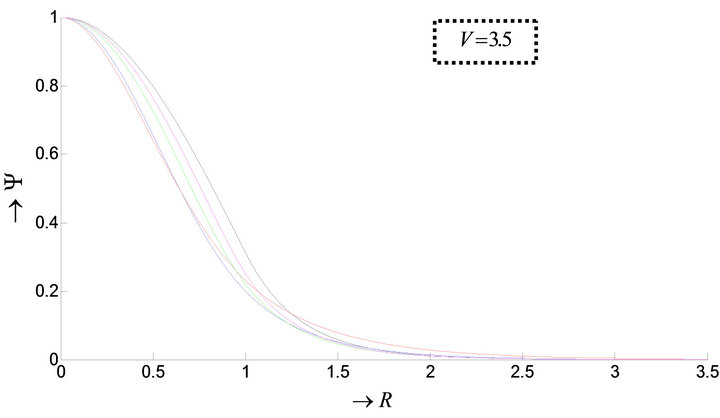 (b)
(b)
Figure 2. (a) Variation of Ψ with R for LP01 mode for different profile exponents; (b) Variation of Ψ with R for LP11 mode for different profile exponents.
From the figures, it can be concluded that as the value of q increases the radial fields of both the modes fall more rapidly inside the core for lower values of q. For both the modes, the curves are found to spread outward in the cladding region as q value decreases.
The Petermann-2 spot size is one of the important characteristics of graded index fiber as it can be used to determine some quantities like splice loss etc.; it is obtained using the modal fields. Tables 1(a) and (b) show the values of WP2 for different q corresponding to LP01 and LP11 modes in graded index fiber.
Petermann-2 spot size decreases more rapidly with increase in V for lower q values. In LP01 mode, this parameter is almost independent of q at V = 3.5; for LP11 mode, it is almost independent at V = 6.
Petermann-2 spot size was determined with Chebyshev Power Series technique in [15] for LP11 mode; it was also compared with an accurate numerical calculation. Those results are very close to our results with Power Series technique in this paper. WP2 consistently falls with increasing V. However, results of [22] are quite contradictory; their WP2 values oscillates with V.
3.2. Variation of Normalized Propagation Constant with the Normalized Frequency
An important parameter that is connected with the normalized propagation constant b is the cut-off normalized frequency V; the condition b = 0 (i.e. when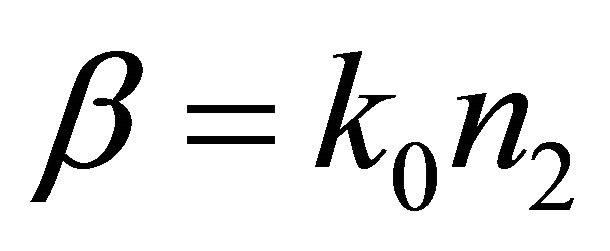 ) is known as cut-off of the mode. The study of b is also required to derive waveguide dispersion. Tables 2(a) and (b) and Figures 1(a) and (b) describe the variation of b with V for different values of profile exponent q including the step index case also. For a particular q, b increases gradually with V and for a particular value of V, it also increases with q.
) is known as cut-off of the mode. The study of b is also required to derive waveguide dispersion. Tables 2(a) and (b) and Figures 1(a) and (b) describe the variation of b with V for different values of profile exponent q including the step index case also. For a particular q, b increases gradually with V and for a particular value of V, it also increases with q.
It was also observed that even for q as high as 200; the profile is far from step index. To get the results for SIF with power series, one has to put  in (8) i.e. to convert the series to Bessel function.
in (8) i.e. to convert the series to Bessel function.
3.3. Cut-Off Frequencies (Vc) for Different Profile Exponents (q) with PSM
Tables 3(a)-(d) show the cut-off V values for some LPlm modes for different q. Applying PSM we have deter-
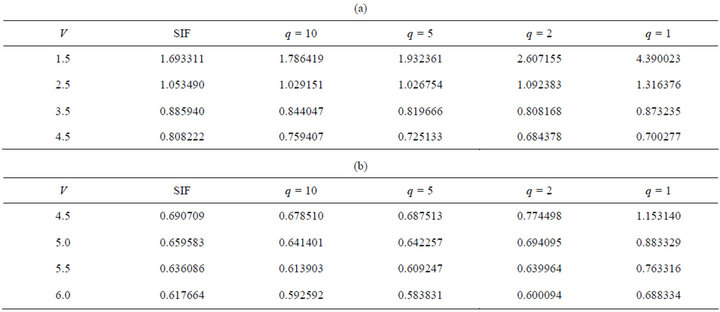
Table 1. (a) WP2-V values for different profile exponents corresponding to LP01 mode with PSM; (b) WP2-V values for different profile exponents corresponding to LP11 mode with PSM.
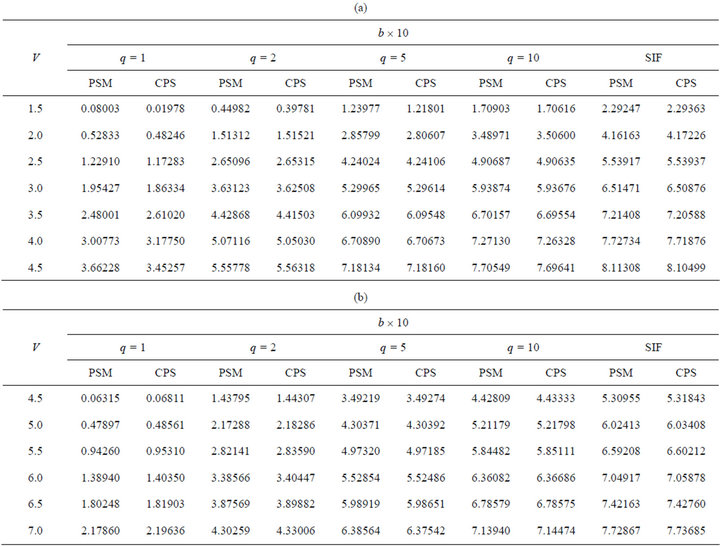
Table 2. (a) b-V values: Direct power series and Chebyshev power series values for different profile exponents corresponding to LP01 mode; (b) b-V values: Direct power series and Chebyshev power series values for different profile exponents corresponding to LP11 mode.
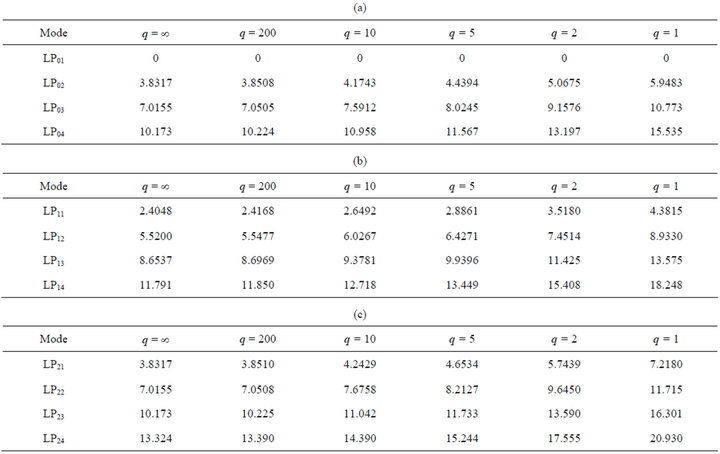
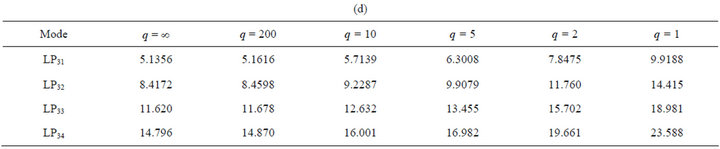
Table 3. (a) q-Vc values: Cut-off frequencies for LP0m modes; (b) q-Vc values: Cut-off frequencies for LP1m modes; (c) q-Vc values: Cut-off frequencies for LP2m mode; (d) q-Vc values: Cut-off frequencies for LP3m mode.
mined the exact values of Vc for any arbitrary profile exponent. In our previous work with CPS technique [15] Vc (LP11) was obtained as 3.5180 for 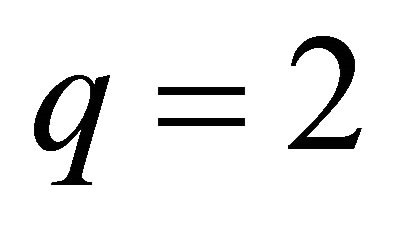 and 4.3816 for
and 4.3816 for . Some of our results of Vc are compared with earlier published results [18-20].
. Some of our results of Vc are compared with earlier published results [18-20].
3.4. Comparison of Cut-Off Frequency Data
In this section, we compare our cut-off frequency results of LP11 mode for different q with the results existing in literature.
From all these data in Table 4, it is evident that this direct power series method provides accurate results for all power-law profiles in graded index fiber.
3.5. Empirical Fit of q-Vc Data
We have tried an empirical form of the following type to
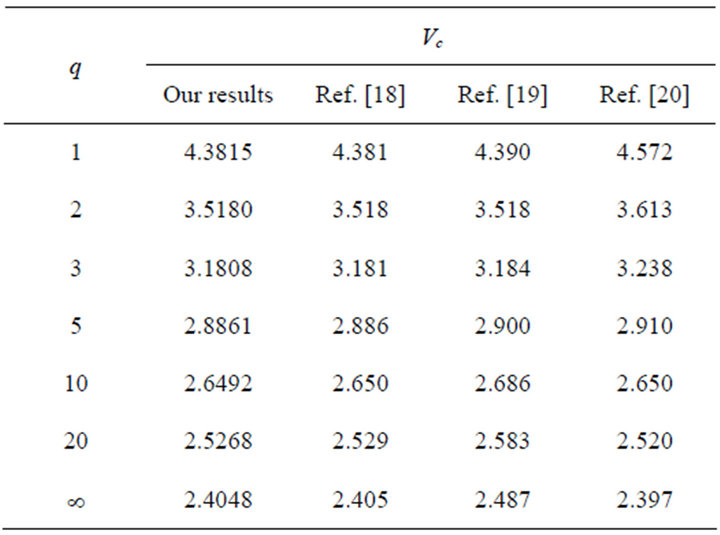
Table 4. q-Vc values: Comparison of cut-off frequencies for LP11 modes Ref. [18]-Matrix method; Ref. [19]-Perturbation method; Ref. [20]-Variational method.
describe the nature of dependence of Vc on q,
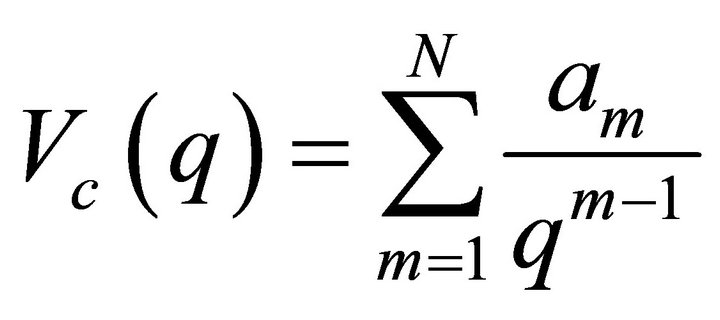 (13)
(13)
N is the number of parameters used. We have fitted  data keeping three and four parameters respectively. The results of different fits are shown in Tables 5(a) and (b) and Figures 3(a) and (b).
data keeping three and four parameters respectively. The results of different fits are shown in Tables 5(a) and (b) and Figures 3(a) and (b).
We have evaluated the values of Vc using the empirical form (13) considering three and four parameters separately for two LPlm modes taking different q. From Tables 5(a) and (b), it is clear that the results obtained fit best with three parameters for LP11 mode and with four parameters for LP02 mode.
For LP11 mode:
Three parameter fit: a1 = 2.403844, a2 = 2.0504123, a3 = −0.527509; maximum error = 0.1714% For LP02 mode:
Four parameter fit: a1 = 3.831020, a2 = 3.788971, a3 = −3.848937, a4 = 2.180391; maximum error = 0.6252% The error in this calculation of Vc using (13) lies within 0.2% in case of LP11 and within 0.7% in case of LP02, which is far better in comparison to previous works [17,18]. Moreover, from Figures 3(a) and (b) it is clear that the estimated values of Vc fit fairly well with those obtained from PSM. So, relation (13) can be considered to give a reasonable estimate of Vc for different q corresponding to different LPlm modes.
4. Conclusion
We have established a general power series method for graded index fibers with a power law profile. It is based on modification of the recursion relations in power series solution of Bessel’s equation and an algorithm to find the co-efficients of the series. Finding the solution comes down to constructing the series with only a simple summation. Here the method has been employed to calculate the propagation characteristics and the cut-off frequencies for graded index fibers of different core index distributions. This method is, no doubt, an accurate one—it has no approximations. It does not pose problems near cut-off or in case of sharp discontinuity. The only care
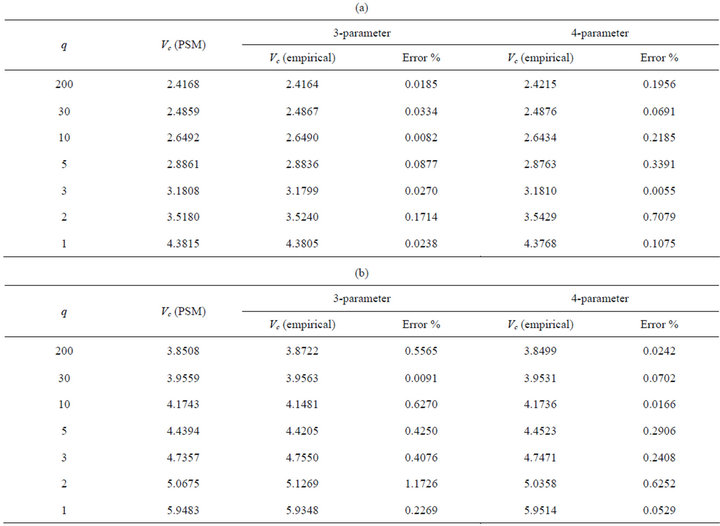
Table 5. (a) q-Vc values: Cut-off frequencies of LP11 mode for different q; (b) q-Vc values: Cut-off frequencies for LP02 mode for different q.
 (a)
(a) (b)
(b)
Figure 3. (a) Variation of cut-off frequencies for LP11 modes. Cross: [q-Vc] data; Solid line: 3-parameter; (b) Variation of cut-off frequencies for LP02 modes. Cross: [q-Vc] data; Solid line: 4-parameter.
one has to take is the convergence of the series for different q value. As q increases, number of terms to be kept in the series expansion required for convergence increases.
REFERENCES
- M. Spajer and B. Charquille, “Application of Intermodal Interference to Fiber Sensors,” Optics Communications, Vol. 60, No. 5, 1986, pp. 261-264. doi:10.1016/0030-4018(86)90147-1
- Z. B. Tian, C. Chen and D. V. Plant, “Optical Fiber Mode Filters in the Dual Mode Fiber Transmission Systems,” IEEE Proceedings of Photonics Conference, Arlington, 9-13 October 2011, pp. 234-235.
- J. Jyothikumar, “All Fiber Spectral Filters Based on LP01 - LP11 Mode Coupling and Applications in Wavelength Division Multiplexing and Dispersion Compensation,” Thesis Submitted, Virginia Polytechnic Institute and State University, Blacksburg, 1996.
- A. Al Amin, A. Li, X. Chen and W. Shieh, “LP01/LP11 Dual-Mode and Dual Polarization CO-OFDM Transmission on Two-Mode Fiber,” Electronics Letters, Vol. 47, No. 10, 2011, pp. 606-608.
- A. Li, A. Al Amin, X. Chen and W. Shieh, “Reception of Mode and Polarization Multiplexed 107-Gb/s CO-OFDM Signal over a Two-Mode Fiber,” Proceedings of Optical Fiber Communication Conference and Exposition, Los Angeles, 6-10 March 2011, pp. 1-3.
- R. Ryf, S. Randel, A. H. Gnauck, C. Bolle, R. Essiambre, P. J. Winzer, D. W. Peckham, A. McCurdy and R. Lingle, “Space-Division Multiplexing over 10 km of Three-Mode Fiber Using Coherent 6 × 6 MIMO Processing,” Proceedings of Optical Fiber Communication Conference and Exposition, Los Angeles, 6-10 March 2011, pp. 1-3.
- N. Hanzawa, K. Saitoh, T. Sakamoto, T. Matsui, S. Tomita and M. Koshiba, “Demonstration of Mode-Division Multiplexing Transmission over 10 km Two-Mode Fiber with Mode Coupler,” Proceedings of Optical Fiber Communication Conference and Exposition, Los Angeles, 6- 10 March 2011, pp. 1-3.
- A. Al Amin, A. Li, S. Chen, X. Chen, G. Gao and W. Shieh, “Dual-LP11 Mode 4 × 4 MIMO-OFDM Transmission over a Two-Mode Fiber,” Optics Express, Vol. 19, No. 17, 2011, pp. 16672-16679. doi:10.1364/OE.19.016672
- M. D. Feit and J. A. Fleck Jr., “Computation of Mode Eigenfunctions in Graded-Index Optical Fibers by the Propagating Beam Method,” Applied Optics, Vol. 19, No. 13, 1980, pp. 2240-2246. doi:10.1364/AO.19.002240
- L. S. Tamil, S. S. Mitra, R. Dutta and J. M. T. Pereira, “Finite Difference Solution for Graded-Index Cylindrical Dielectric Waveguides: A Scalar Wave Approximation,” Applied Optics, Vol. 30, No. 9, 1991, pp. 1113-1116. doi:10.1364/AO.30.001113
- M. R. Shenoy, K. Thyagarajan and A. K. Ghatak, “Numerical Analysis of Optical Fibers Using Matrix Approach,” Journal of Lightwave Technology, Vol. 6, No. 8, 1988, pp. 1285-1291. doi:10.1109/50.4132
- K. Okamoto and T. Okoshi, “Analysis of Wave Propagation in Optical Fibres Having Core with α-Power Refractive Index Distribution and Uniform Cladding,” IEEE Transactions of Microwave Theory and Techniques, Vol. 24, No. 7, 1976, pp. 416-421.
- A. Sharma and A. K. Ghatak, “A Variational Analysis of Single Mode Graded-Index Fibers,” Optics Communications, Vol. 36, No. 1, 1981, pp. 22-24. doi:10.1016/0030-4018(81)90022-5
- S. Gangopadhyay, M. Sengupta, S. K. Mondal, G. Das and S. N. Sarkar, “Novel Method for Studying Single Mode Fibers Involving Chebyshev Technique,” Journal of Optical Communications, Vol. 18, No. 2, 1997, pp. 75-78.
- I. Dutta, A. R. Chowdhury and D. Kumbhakar, “Accurate Estimate of Some Propagation Characteristics for the First Higher Order Mode in Graded Index Fiber with Simple Analytic Chebyshev Method,” Journal of Optical Communications, Vol. 34, No. 1, 2013, pp. 33-41.
- W. A. Gambling and H. Matsumura, “Propagation in Radially-Inhomogeneous Single-Mode Fibre,” Optical and Quantum Electronics, Vol. 10, No. 1, 1978, pp. 31-40. doi:10.1007/BF00620241
- W. A. Gambling, H. Matsumura and C. M. Ragdale, “Wave Propagation in a Single-Mode Fiber with Dip in the Refractive Index,” Optical and Quantum Electronics, Vol. 10, No. 4, 1978, pp. 301-309. doi:10.1007/BF00620118
- E. K. Sharma, I. C. Goyal and A. K. Ghatak, “Calculation of Cut-Off Frequencies in Optical Fibers for Arbitrary Profiles Using the Matrix Method,” IEEE Journal of Quantum Electronics, Vol. 17, No. 12, 1981, pp. 2317-2321. doi:10.1109/JQE.1981.1071045
- J. P. Meunier, J. Pigeon and J. N. Massot, “Perturbation Theory for the Evaluation of the Normalized Cut-Off Frequencies in Radially Inhomogeneous Fibres,” Electronics Letters, Vol. 16, No. 1, 1980, pp. 27-29. doi:10.1049/el:19800023
- K. Hotate and T. Okoshi, “Formula Giving Single-Mode Limit of Optical Fibre Having Arbitrary Refractive Index Profile,” Electronics Letters, Vol. 14, No. 8, 1978, pp. 246-248. doi:10.1049/el:19780167
- A. Ghatak and K. Thyagarajan, “An Introduction to Fiber Optics,” Cambridge University Press, Cambridge, 1999.
- A. Bose, S. Gangopadhyay and S. C. Saha, “A Simple Method of Prediction of Fractional Modal Power Guided inside the Core, Excitation Efficiency of the Mode by Uniform Light Source and Petermann I and II Spot Sizes: All for First Higher Order Mode in Graded Index Fibers,” Optik, Vol. 122, No. 3, 2011, pp. 215-219. doi:10.1016/j.ijleo.2009.12.011

