Received 6 January 2016; accepted 18 April 2016; published 21 April 2016

ABSTRACT

We want to conclude on the interest of the “crimping” process used to produce the glass wool and to make a comparison for anisotropic factor obtained from structural property (air permeability) as well as thermal property (thermal conductivity and diffusivity). The main structural (densities, porosity, specific surface, air permeability) and the thermal (conductivity, diffusivity, heat capacity) characteristics of this glass wool are presented. Thermal results are determined by using several methods (Hot disc (HD), Heat Flow Meter (HFM) and Guarded Hot Plate).

Keywords:

Fibrous Insulation Material, Glass Wool, Air Permeability, Thermal Conductivity, Anisotropic Factor

1. Introduction

The industrialized countries have engaged, since the energy crisis of 1974, a policy of energy saving which has caused a considerable development of the heat insulation sector in the construction industry. Nowadays, the energy consumption of building accounts over 40% of final energy consumption in the European Union. The main solution for reducing the energy consumption is to increase the thickness of the thermal insulation inside the building envelopes. But the knowledge of the insulating materials thermal behaviour is very imperfect in spite of the interest [1] . Heat exchange in fibrous heat insulating materials which constitute highly disperse gas filled systems is complex. Effective thermal properties are determined in order to take into account: 1) the heat transfer process which includes conduction, radiation and convection; 2) the mass diffusion process and 3) the anisotropy of the structure. Assuming in a first approach that fibres (or pores) are randomly oriented in all directions, the resulting effective conductivity is therefore isotropic [2] . This simplification makes it possible to study other complicated mechanisms such as temperature dependence of the effective thermal conductivity at elevated temperatures [3] . The overall thermal conductivity in porous media containing randomly oriented pores, evidenced by the large volume of publication in the past two decades, has been studied [4] . For the case of randomly oriented pores, the overall thermal conductivity strongly depends on the internal heat transfer across the pore surfaces [5] . The apparent conductivity is principally due to the heat transfer through the gas [6] .

There is a need of studying material structural properties in order to analyze and interpret thermal behavior. The present work presents three main characteristics of glass wool structure: volume ratio of the solid phase to the total volume (porosity), degree of fragmentation in the solid phase (specific surface), and spatial organization of the solid phase (anisotropic factor). Glass wool object of this study is not an ordinary insulation material. This material has been produced by an innovated crimping process described by Bergonnier et al. [7] . The anisotropic factor is determined from thermal conductivity and diffusivity experimental values, and air permeability measurements are compared. We conclude on the impact of the crimped process by comparing the anisotropic factors obtained by these experimental methods with literature value for ordinary glass wool.

2. Materials

Glass wool intended for the insulation of roofs has been studied. Porous fibre materials contain three components: fibre, air and binder. The content of the components and their properties and arrangement determine the material structure. Before the curing stage, the fiber mat is processed to produce a structure endowing the material with a stronger mechanical resistance (to compression, tearing, or shear). This step is called “crimping”. It consists in breaking the naturally layered structure of the mat, through an on-line transverse and axial compression. The denser layers are buckled during the axial compression in order to produce a more isotropic fiber orientation (Figure 1), and in particular, a larger population of vertical fibers. Mechanical stiffness and strength are much higher than for the initially layered material, as shown in the work of Bergonnier et al. [7] . Binders appear (Figure 2) in the form of droplets and clusters and they are distributed fairly regularly along the fibers. The average thickness of the binder is estimated at about 500 nm. Fibers are made, in a large proportion, of recycled glass and its chemical composition is classified into the classic E-type [8] . Typical compositions are 90% glass fibers and 10% binder. The exact composition of our glass wool has not been exactly determined, but similar wools have been studied in other works which give their detailed composition [7] . Scanning Electron Mi-

croscopy (SEM, Quanta 200 FEG Environmental) shows heterogeneity of the geometry of fibers and the random distribution of fibers (Figure 2 [8] ). In principle, all size (length and thickness) of fibers can be used for heat- insulating materials in construction. However, thin (d = 4 to 12 µm) and thick (d = 13 to 15 µm) are preferable. A statistical exploitation of the imagery shows a mean diameter of 13 m diameter which correspond to thick fibres.

3. Structural Characterizations

3.1. Density and Porosity

The bulk density ρ₀ can be determined from the expression:

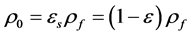(1)

where ε_s and ε are the part by volume of, respectively, solid and gas (porosity) in the highly disperse systems and ρ_f is the true density of the fiber (usually equal to 2500 - 2800 kg∙m⁻³) for glass. To assess the total porosity (if non-accessible porosity like closed porosity is neglected), for materials like masonry, a specimen of the material is submitted to a vacuum pressure to extract air, before immersing it into distilled water. But, for fibrous specimen, this method could not be used because water is not retained and an expansion of the bulk structure is observable. If the true density of the fiber is known, Equation (1) can be used. In this work, we have preferred applying relation (2).

(2)

Specimen has been dried inside an oven regulated at the temperature of 40˚C during 3 hours. The mass of the specimen is measured by a Mettler Toledo (LJ16) weighting machine in order to check the moisture content of the specimen. Bulk density ρ₀ is determined from mass measurement of a known volume of material. True density ρ_v is determined by a helium pycnometer (Accupyc 1330). Helium is an inert fluid for the fibrous structure. A specimen is putting inside a cylindrical cell. A volume (V = 10 cm³) has been chosen because of the elementary volume representative (EVR) of the material function principally here of the fiber thickness. Results are presented in Table 1.

The experimental deviation obtained for the true density measurement is 41.4 kg∙m⁻³ (or 1.6%). Deviation for determining bulk density can be estimated to 3% with apparatus accuracies. As bulk density is higher (Table 1) than 20 kg∙m⁻³, glass wool can be classified in the category of heavy insulation materials like most of the insulation wools used in the building industry. Glass wool presents an important porosity near 97%.

3.2. Specific Surface

Specific surface (S_p) expresses the degree of division of the solid phase. For heat and mass transfer, a shape with higher specific surface value is more efficient. For a given volume V (or material mass), different geometric shape generate different amounts of surface area (A_sg) by which to interact with the environment. Volumetric surface (S_V) and specific surface (S_m) can be determined as:

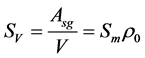(3)

An Accelerated Surface Area Porosimeter (ASAP, Micromeritics’s ASAP 220) has been used to determine the specific surface experimentally. Method is based on the fact that materials present open porosity which adsorbs surrounding gas. ASAP used with krypton’s content lower than 35% automatically determines by applying BET model specific surface. Important value (S_m= 0.2332 m²∙g⁻¹) is obtained showing that material is finely divided.

3.3. Air Permeability and Anisotropic Factor

An air permeability tester (TEXTEST FX 3300) has been used to determine the permeability of the glass wool samples [9] . The measurement principle consisted in applying a pressure drop ΔP (Pa) on a given area A (m²) of the material. When the flux is steady across the sample thickness, the air velocity V_s (mm∙s⁻¹) is given by the apparatus. The test standard ISO 9237 (1995F) for industrial fabrics has been applied in this work. This test recommends a surface area of 20 cm², a pressure drop 200 Pa and requires that the samples were preliminarily conditioned in a standard atmosphere of 20˚C and a relative humidity of 65%. The air permeability k_A (m∙s⁻¹) is measured in the three principal directions of the sample as depicted in Figure 3. k_A//1 and k_A//2, refer to the permeability tensor components parallel to the direction of stratification. k_A//1 is the component in the direction parallel to the fibers, while k_A//2 is the component in the direction perpendicular to the fibers. The air permeability

in the third direction, , is measured perpendicularly to the stratification plane, and corresponds to the direction of the heat flow when the glass wool is in use.

The anisotropic factor AF is determined by the ratio of the parallel air permeability to perpendicular permeability:

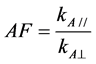(4)

A series of five measurements for each direction has been performed. An anisotropy factor (AF) of 1.55 is obtained. This value is lower than common glass wools [1] value equal to 2. Anisotropy has been reduced by the “crimping” process.

4. Thermal Conductivity Characterization

4.1. Experimental Procedure

There are a variety of methods for the measurement of the thermal conductivity. They are broadly classified as steady-state methods and transient methods. Due to important density (more than 75 kg∙m⁻³), total heat transfer in glass wool is principally due to transfer in gas (Figure 4) [6] . Transfer by radiation and conduction in solids can be considered as negligible.

The most adapted technique for insulation materials (American ASTM C 177-97 and European ISO 8302 Standards) taking into account the total heat transfer is the steady-state methods and particularly the guarded hot plate (GHP). Another traditional steady-state method is the Heat Flow Meter (HFM) method (American ASTM C 518-98 and European ISO 8301 Standards). The GHP as other steady-state methods suffer from major drawbacks. They require a long time to establish a steady-state temperature gradient across the sample, and this temperature gradient is required to be large. Sample size is also required to be large and contact resistance between the thermocouple and the sample surface is considered a major source of error. Some material properties can be altered during the time to achieve steady state.

Transient techniques measure a response (temperature, flow) to thermal signal (flow). Therefore, these techniques are distinguished mainly by the short time required to obtain the desired results. Hot strip can be used to measure the thermal diffusivity and conductivity of solid non-electrically conducting materials. The most recent development of the hot strip method is the Hot Disc (HD) technique. The basic principle of this method relies on a plane element which acts both as temperature sensor and heat source [10] [11] . This element consists of an electrically conducting pattern of thin nickel foil (10 µm) spiral shaped, embedded in an insulating layer usually made of Kapton (70 µm thick). The HD probe is located between two samples with both sensor faces in contact with the two samples surfaces of similar characteristics. One of the most important parameter is called probing

depth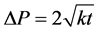. The probing depth must therefore be lower than the thickness of this sample to validate the infinite sample assumption. In addition, an optimal experimental time should be determined as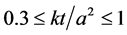

to optimize the best combination of sensitivity coefficients for the estimation of the thermal conductivity and thermal diffusivity property. Temperature increased must be also lower or equal to 1˚C. Considering the thermal characteristics of glass wool in literature, a radius sensor of 14.63 mm is used. Sample thickness and diameter is over respectively 30 mm and 90 mm in order to respect the infinite media hypothesis.

4.2. Results

According to ISO 8302, guarded hot plate (GHP) has been used to determine thermal conductivity of glass wool L1 against sample mean temperature (Figure 5). Dimension of the sample is 246 × 250 × 60 mm. About 6 hours are necessary to achieve the temperature difference of 10˚C between the two external surfaces of the sample as required by the ISO 8302 standard. This equilibrium is obtained by using 0.4 W thermal flow. This procedure is repeated for successive mean sample temperatures of 10˚C, 20˚C, 30˚C and 40˚C. At the temperature of 10˚C (standard value), thermal conductivity is: l = 0.0369 ± 0.0007 W∙(m∙K)⁻¹. Variation of thermal conductivity (l) against sample mean temperature (MT) shows linear curve defined as l = 0.03443 + 0.000244.MT (R-squared: 99.28%). Measurement error of 7% is recommended by ISO 8302 standard. Error bars have been reported in Figure 5 as well as HFM and Hot Disc experimental values.

Bulk anisotropic module of Hot Disc method has been used to determine thermal conductivity and thermal diffusivity in axial and radial directions (Figure 5 and Table 2). The output power and measuring time is respectively equal to 20 m∙W and 160 s. We have chosen to select time test recommended by International Stan-

dard ISO 22007-2. In the case of the flow, recommended value of 0.1 W induces a temperature increase greater than 1. We have chosen 20 mW the minimal value can Hot Disc accepts but it creates an increased temperature of 1.24˚C. Due to the low thermal conductivity of glass wool, it is very difficult to respect the maximal increase of 1˚C: one of the conditions for a good test. Results are obtained for a characteristic time of 0.528 s and a probing depth of 21.3 mm.

Axial conductivity (l_a) is referred to as through-plane in sample perpendicularly of the thermal probe. In our case, axial conductivity is in the same direction of k_A//1 and k_A//2 (Figure 3). Radial conductivity (l_r) is referred to as in-plane in sample (similar direction in the sample to k_A^ in Figure 3 and corresponds to the direction of heat flow in building use. Coherent values have been obtained from guarded hot plate (GHP), high flow meter (HFM) and hot disc (in radial direction only) but not with results from hot disc in axial direction. Another point of interest is to compare thermal conductivity against porosity from literature values [12] . We can notice the lowest thermal conductivity value is obtained for 97% porosity (Figure 6). Compared to literature values, thermal conductivity of our wool is more important. Crimped process can be an explanation.

Hot disc method allows determining thermal conductivity in three principal directions of the sample. As before by air permeability, an anisotropy factor is defined as the ratio of conductivity corresponding to a heat transfer along the plane of stratification with the conductivity corresponding to a heat transfer perpendicular to the plane of stratification. The ratio axial conductivity against radial conductivity is equal to 1.32 in the dry state (Table 2). This value is close to air permeability anisotropic factor (Table 3). We can notice than the same ratio is obtained for conductivity (AF_λ) and diffusivity (AF_a).

These remarks confirm thermal conduction and diffusion are mainly sent through the pores by the air inside pores.

5. Conclusion

Glass wool tested is not an ordinary one because it has been produced by a crimping process. Consequently a lower anisotropic factor (equal to 1.4) is obtained by air permeability measurement instead of a factor equal to 2

usually found. We have determined other structural parameters in order to characterize high porosity (97% from true and bulk densities) and finely divided structure (high specific surface of 0.2126 m²∙g⁻¹). A comparison between experimental results from air permeability and thermal conductivity has been done. The same anisotropic factor is obtained showing the coherence between results from structural and thermal parameters. Thermal conductivities are measured from several methods: Guarded Hot Plate (GHP), High Flow Meter (HFM), Hot Disc. Coherent values have been obtained between these methods although needed establishment of steady state and Hot Disc is transient method. However, we have noticed that radial values are coherent but not axial ones. Anisotropy in thermal conduction and diffusion is not taking into account for the moment in the heat calculations in the case of French thermal rules.

Acknowledgements

The authors would like to express deep gratitude to J-B Rieunier ISOVER as well as the technical staff of UPJV microscopic platform Amiens, ENSAIT-GEMTEX Roubaix and LASIE La Rochelle University.

Cite this paper

Laurent Marmoret,Hussein Humaish,Anne Perwuelz,Hassen Béji, (2016) Anisotropic Structure of Glass Wool Determined by Air Permeability and Thermal Conductivity Measurements. Journal of Surface Engineered Materials and Advanced Technology,06,72-79. doi: 10.4236/jsemat.2016.62007

References

NOTES

^*Corresponding author.