Journal of Surface Engineered Materials and Advanced Technology
Vol.05 No.01(2015), Article ID:52970,11 pages
10.4236/jsemat.2015.51006
Experimental Adsorption and Modelisation of CO2 on Adsorbents Collected from Elborma Field in South Tunisia
Souhail Bouzgarrou1, Hadi Jedli2, Nadra Stiti3, Nourdine Hamdi4, Khalifa Slimi5, Mohamed Bagana3
1Research Unity of Energetic and Environment, National Engineering School of Tunis, Tunis El Manar University, Tunis, Tunisia
2Department of Energetic, National Engineering School of Monastir, Monastir, Tunisia
3Materials Research Laboratory Department of Chemical, National Engineering School of Gabès, Gabès, Tunisia
4Department of Material, Higher Institute for Water Science and Technologies of Gabès, Gabès, Tunisia
5Higher Institute for Transport and Logistics of Sousse, Sousse, Tunisia
Email: s_bouzgarrou2002@yahoo.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 November 2014; revised 18 December 2014; accepted 29 December 2014
ABSTRACT
In order to select the best adsorbant for CO2 sequestration, this study deals the interaction between clay, Triassic sandstone and Jurassic evaporate and CO2. These materials have been used as sorbents. To choose the adequate geological layers for sequestration and with minimum risk of leakage, adsorbent characterizations were investigated using X-ray diffraction, SEM and surface area analysis, structural and textural shapes of these materials have been investigated too. The elution chromatography in gaseous phase has been employed to determine the adsorption isotherms of adsorbed CO2 for each adsorbent. Then, the treatment of the experimental data allowed us to compare each CO2/adsorbent couple. The adsorption isotherms were modeled using the Langmir and Freundlich models. A thermodynamic comparison between the different adsorbents will also be provided. Experimental results show that clay and Triassic sandstone have the highest rate of adsorption amount. It has been also found that the Langmuir model is the most appropriate one to describe the phenomenon of CO2 adsorption on clay. However, for the other adsorbents (i.e. Triassic sandstone and Jurassic evaporates) the two-models are adequate.
Keywords:
Adsorption Selectivity, Geologic Materials, Surface Area Analysis, Elution Chromatography, Langmuir, Freundlich Modelisation

1. Introduction
Regulating CO2 emissions into the atmosphere has become a crucial target since the scientists’ statement that the earth’s climate is changing and the average temperature of the planet is getting higher and higher due to modern human activities [1] . In fact, greenhouse gases’ concentrations are higher nowadays than that at any time previously.
To tackle this problem, geological sequestration of CO2 is one of the main options to reduce CO2 emissions in order to mitigate the greenhouse effect [1] [2] . Aquifers that are deep and separated from underground sources of potable water can be excellent sites for large-scale CO2 storage. Moreover, a large number of such saline aquifers exist in the depths of sedimentary basins throughout the world and various solid materials such as calcium oxide or lithium oxide [3] [4] and silica gel readily adsorb carbon dioxide.
The capture and sequestration of CO2 problems, actually well-documented, are classified within the scope of the general problem of the greenhouse effect and global warming particularly, through the activities of the IPCC synthesis (International Panel on Climate Change) established in 1988 under the auspices of the United Nations [5] . The CO2 capture and sequestration in deep saline aquifers has emerged as an appropriate solution to reduce greenhouse gas emissions. The effectiveness of this option depends mainly on the sequestration at a low transfer rate of aquifers, sequestration potential as a residual, by adsorption or mineralization in the form of carbonate structure [6] .
CO2 adsorption on dry sorbents has fascinated many researchers. CO2 adsorption capacity is needed for practical applications [7] . In this study, clays, Triassic sandstone and Jurassic evaporate are chosen as potential adsorbents to measure the CO2 adsorption amount. These materials come from real sits considered for CO2 sequestration in the southern region of Tunisia. CO2 adsorption by porous materials in deep saline aquifers is a very promising option since this operation reduces the possibility of leakage from the storage tank. On the other hand, a big amount of the injected CO2 in the deep aquifer can migrate to the top of the aquifer by buoyancy forces due to density difference. As a result, this quantity of CO2 will be adsorbed by the cap-rock layer of the tank. This operation depends strongly on the time and physical properties of materials which comprise the cap-rock (porosity, specific surface, mineralogical composition…) and the chemical properties (acidity) as well as the nature of the adsorbed molecules.
Depending on the nature of the interactions between the adsorbent and the adsorbate, one can distinguish two- adsorption types. The first one is the physical adsorption which is attributed to lower links of physical interaction energies basically between 5 and 40 kJ/mol. The involved forces are of the Van Der Waals type due to electrostatic interactions which are small forces that can be easily broken. This is a reversible and exothermic phenomenon that can occur without changing the molecular structure of the solid [8] . However, the second one is chemical adsorption or chemisorptions, corresponding to strong chemical links with the binding energy which is large enough than 80 kJ/mol [9] . It involves chemical reactions between the surface of the adsorbent and the adsorbate molecules. It involves chemical reactions between the surface of the adsorbent and the adsorbate molecules. In this context, we are interested in assessing the best adsorbent for CO2 capture. The present work aims to select an efficient adsorbent well suited to the capture of CO2 and therefore to its storage for a long period of time. A study of the major intrinsic characteristics of different adsorbents will be performed. This study allowed us to evaluate the best material able to adsorb the maximum of CO2 and therefore to optimize the choice of the storage site.
2. Materials and Methods
Three samples have been selected in this study: clay from the cap-rock layer having a green color (from the city of Gabes, Tunisia); Triassic sandstone sample which is composed of coarse sandstone and conglomerate of large siliceous stone. It is a natural adsorbent gray in color from El Borma field located in southern Tunisia, and used essentially for storage. The Jurassic evaporates are gray natural materials from deep saline aquifers in southern Tunisia, collected from the cap-rock of the reservoir. The lower layer of Jurassic evaporates is supported by a slightly discordant stratification on the Triassic sandstone.
The method used to determine the CO2 adsorption isotherms on different adsorbents is based on the principle of gas-phase chromatographic method (Figure 1). Preliminary work consists in characterizing the different selected adsorbents (i.e. Clay, Jurassic evaporates and Triassic sandstone).
For each selected adsorbent, we are interested in determining the equilibrium conditions in the column. Hence, adsorption studies were conducted by varying two-factors: the velocity and pressure of the injected CO2. This was done by injecting the same amount of CO2 for all adsorbents. The variation of these two-factors allows us to estimate the flow and pressure of the injected CO2 required reaching thermodynamic equilibrium inside the column. Powder XRD patterns were obtained using a Panalytical X-Pert high score plus diffractometer in the range 3˚ - 70˚ 2q, at a scanning rate of min−1 and employing Cu Kα filtered radiation.
2.1. Adsorbents Characterization
Table 1 shows the chemical composition (wt%) data of the selected three samples. The data indicate that the percentage of SiO2 in clay and Triassic sandstone samples was relatively high. This is consistent with the presence of quartz as shown by XRD [Figure 2(a)]. The higher concentration of Na ion in the evaporate sample confirmed the presence of the halite. The percentage of the K2O in the clay and Triassic sandstone show that the illite is the major compound in both samples.
Figure 2 presents the XRD patterns of three powder samples. As illustrated by this figure, the clay sample [Figure 2(a)] essentially comprises illite (10 Å) and kaolinite at 7.16 Å; the associated minerals are dolomite (2.88 Å) and quartz (3.34 Å). X-ray diffraction analysis of the evaporate sample shows the presence of halite at 2.82 Å and 1.99 Å [Figure 2(b)]. The Triassic sandstone samples are composed of illitic and kaolinitic clay associated to quartz [Figure 2(c)].
The SEM analysis (Figure 3) exhibits the morphology of the three soils. The SEM imaging shows that the particle morphology is laminated. This is due to the clay fraction in the sample represented by the layers of argillaceous form. In the case of Jurassic evaporates, the particles have a spherical form with very small compared to the others samples.
In Table 2, we provide the textural characteristics of these different materials obtained with the Nitrogen adsorption technique. The specific surface area and the total pore volume are the most important characteristics of adsorbents. For all samples, the SBET is relatively lower and the clay sample has the highest specific surface area. The total pore volumes of these samples are comparable.
Figure 1. Schematic diagram of the experimental set-up.
Table 1. Chemical composition of different adsorbents.
Table 2. Textural characteristics of different adsorbents.



Figure 2. X-ray diffraction patterns of cuttings samples of (a) Clay; (b) Jurassic evaporates and (c) Triassic sandstone.



Figure 3. SEM images of (a) Clay; (b) Jurassic evaporates and (c) Triassic sandstone.
2.2. Operating Mode
In this study, a gas chromatograph series IGC 10 M was used to study the adsorption of CO2 on the following adsorbents: clay, Triassic sandstone and Jurassic evaporate. It is worth noting that the most important difference between these samples is the particle size and the outer surface.
After filling with a given mass of adsorbate, the adsorption column is conditioned with a stream flow of CO2 and heated to a temperature of about 120˚C during 24 hours to remove any residual moisture. Then, the system is cooled to the ambient temperature. CO2 is introduced directly into the chromatograph through a manual injection valve (Figure 1).
We balance the katharometer at each injection; check the flow rates of the gas in the reference column and that adsorbed. Then, a definite amount of CO2 is adsorbed for a given injection pressure, depending on the flow rate value and injection temperature, an electrical signal in the form of a chromatographic peak is obtained on a recording paper.
At this stage, one can detect the coordinates in each chromatogram point using a Matlab program based on the trapezoidal method.
3. Results and Discussion
3.1. Choice of Equilibrium Conditions
The adsorption experiments were conducted to estimate the gas flow rate and the pressure of CO2 injected at the inlet in order to reach thermodynamic equilibrium inside the column. For this purpose, we inject a fixed amount of CO2 in a column filled with a mass mb of adsorbent, at a velocity Vinj and a specific temperature Tinj. Then, we vary the flow vector gas, D, setting the pressure of the injected CO2 from the inlet. Table 3 summarizes the equilibrium conditions inside the column for each adsorbent. The adsorption experiments were conducted to estimate the gas flow rate and the pressure of CO2 injected at the inlet in order to reach thermodynamic equilibrium inside the column. For this purpose, we inject a fixed amount of CO2 in a column filled with a mass mb of adsorbent, at a velocity Vinj and a specific temperature Tinj. Then, we vary the flow vector gas, D, setting the pressure of the injected CO2 from the inlet. Table 3 summarizes the equilibrium conditions inside the column for each adsorbent.
3.2. Adsorption Isotherms
For each pair CO2/adsorbent, we have made several injections at different temperatures. The obtained experimental results are shown in Table 4.
The study of Figure 4 shows that all the CO2 adsorption isotherms on the selected adsorbents have the same shape and are of type I according to the classification of BDDT. Therefore, we can conclude that basically a
Table 3. Equilibrium conditions inside the column.
Table 4. Results obtained from the isotherms of selected adsorbents.



Figure 4. Adsorption isotherms of (a) CO2/Clay; (b) CO2/Triassic sandstone and (c) CO2/Jurassic evaporate at different temperatures.
monolayer adsorption takes place for all the adsorbents in the fixed operating conditions.
Furthermore, the isotherms show no flat curves, indicating that the adsorption sites are not saturated in the range of the introduced amount of CO2. In all cases, the largest adsorption capacity occurs at the lowest temperature (room temperature) and decreases with the increase of the injection temperature. This is obvious since we are dealing with an exothermic adsorption phenomenon.
3.3. Modeling of Adsorption Isotherms
Langmuir and Freundlich models are extensively used to model adsorption isotherms of CO2 on different adsorbents [11] -[13] .
The Langmuir model is used to calculate the maximum adsorbed amount qm to form the monolayer as well as the adsorption constant KL [14] [15] . These parameters are determined using the linearization of the model [equation (1)] by plotting 1/q vs. 1/P.
The linear form of Langmuir model equation allows us to determine the parameters of this model (i.e. qm and kL). This model is given by the following equation [16] [17] :
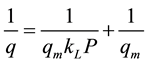 (1)
(1)
When we plot 1/q as a function of 1/P, one can obtain a straight line with a slope 1/qmKL that intercepts 1/p- axis at 1/qm. Then, the two-parameters of this model can be deduced.
It is important to note that Langmuir model is a good representation of adsorption isotherms of type I.
The Freundlich model parameters n and K are also determined by the linearization of the empirical model [Equation (2)] by plotting 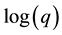 as a function of
as a function of

where K is the Freundlich constant which is mainly related to the maximum adsorption capacity and n a constant characterizing the interaction between adsorbate and adsorbent. In general, this model is valid for the monolayer adsorption on heterogeneous surfaces, where the adsorption sites are different in nature [17] [18] .
By plotting 



The analysis of Table 5 shows that the Langmuir model describes correctly the adsorption isotherms of CO2 on clay for all fixed temperatures with a correlation coefficient R2 between 0.9995and 0.9998. The high values of the correlation coefficients obtained in the case of CO2 adsorption on clay are in agreement with the basis of Freundlich model, involving surface heterogeneity.
It is important to highlight that above 46˚C, the maximum capacity qm predicted by the Langmuir model is systematically lower than the adsorbed amounts [12.0482 ´ 10−3 (g/g)]. However, the capacity qm must be greater than or equal to the adsorbed quantities calculated from the isotherm curves. Although, the correlation coefficients are satisfactory (between 0.9971 and 0.9996), the values of qm are meaningless.
The Freundlich model parameters n and K are also provided (Table 6). As it is well known, lower values of
Table 5. Parameters of langmuir and freundlich for clay.
Table 6. Parameters of langmuir and freundlich for the triassic sandstone.
n imply a higher heterogeneity of sites [19] . In our case, n is higher than 1 which implies that heterogeneity of sites is lower. In addition, the K values vary slightly with temperature.
From Table 6, it comes out that the Langmuir model describes adequately the experimental data of adsorption of CO2 on the Triassic sandstone for all the tested temperatures with a correlation coefficient R2 between 0.9992 and 0.9998. Therefore, the experimental adsorption isotherms can be linearized according to the Langmuir model. In addition, the CO2 adsorption isotherms of the Triassic sandstones can be correctly described by the Freundlich model. The obtained correlation coefficients imply a high surface heterogeneity. Furthermore, the value of n is greater than 1 indicating that the heterogeneity of sites is low. Results show also that K values are strongly subordinate with temperature and that adsorption sites are not energetically homogeneous.
It is worth noting that for a temperature above 27˚C, the maximum capacity qm predicted by the Langmuir model is below the maximum capacity qm for the same temperature obtained from the adsorption isotherms. Thus, qm values seem to be coherent and meaningful. According to Table 7, the Langmuir model describes well the experimental data. It reflects a localized adsorption on homogeneously-distributed sites. The Freundlich model describes appropriately the adsorption isotherms for the couple CO2/(Liassic evaporates) for different temperatures values. Moreover, the changes in the Langmuir parameters are not regular with temperature.
It is important to note that for all temperatures, the maximum adsorbed amounts of CO2 (i.e. qm) predicted by the Langmuir model are systematically lower than the adsorbed amounts corresponding to an injected amount of CO2 equal to 0.42 cm3. However, the values of qm should logically be higher or equal to the quantities adsorbed when plotting isotherms [7 ´ 10−3(g/g)]. Thus, the obtained values of qm are meaningless, even if the Langmuir curves are satisfactory.
Then, we can conclude that the Langmuir model does not allow us to describe correctly the adsorption isotherms of CO2 on the Jurassic evaporate. In addition, the values of KL indicate a low affinity of CO2 on evaporate with relatively-homogeneous sites.
3.4. Thermodynamics Adsorption Study
In order to determine the adsorption nature for each adsorbent, we have calculated the enthalpy of adsorption based on the Clausius-Clapeyron equation.

Obviously, the isosteric enthalpy of adsorption ΔHads is an important thermodynamic property in gas-solid adsorption problems. Then, it is necessary to draw the isosteric isotherms obtained at different temperatures. To this end, we have plotted the variation of 
We note that the curves ΔHads as a function of q for all adsorbents (Clay, Triassic Sandstone and Jurassic evaporates) [21] , not shown here for the sake of brevity, present negative values which confirm the exothermic nature of the adsorption phenomenon. In addition, the comparison between enthalpy adsorption values against available literature values are within the magnitude of the physical adsorption [20] [22] . We note also that the variation of isosteric enthalpy is small for clays and evaporates, showing that the heterogeneity of their sites is low.
In Table 8, the adsorption enthalpies of the different three couples studied here are depicted. In terms of CO2 adsorption on clay, the average isosteric heat of adsorption is equal to 3.2904 kJ/mol. Variations in enthalpy as a function of the adsorbed amount are quite small for this material, suggesting that the heterogeneity of its surface is low, for the Triassic sandstone, the enthalpy of adsorption appears as an increasing function of the adsorbed amount or recovery rate and the isosteric heat of adsorption is equal to 6.5007 kJ/mol. For Jurassic evaporates, one can see that the enthalpy of adsorption decreases when the amount adsorbed increases. This can be explained by the fact that the adsorption of molecules on the first layer is on the first parts of the surface having the highest interaction energy. The adsorption of the molecules results in heat generation with an average isosteric adsorption heat equal to 5.6990 kJ/mol.
Table 7. Parameters of Langmuir and Freundlich for the Liassic evaporate.
Table 8. Adsorption enthalpies for different adsorbents.
3.5. Comparative Study of Adsorbents
In this section, we aim to develop a comparative study between the adsorbents in order to choose the most efficient one for the adsorption of carbon dioxide CO2.
Based on the previous discussions, the CO2 adsorption on different materials is exothermic. Indeed, the temperature plays an important role as it influences the adsorption capacity by affecting the amount of the adsorbed CO2 molecules. It has been observed that the number of molecules in the column at the equilibrium decreases with temperature. Therefore, the best adsorption capacity of CO2 is obtained at a low temperature, (i.e. for a temperature close to room one). The adsorbed amount of CO2 on different adsorbents at low temperatures is illustrated in Table 9.
Increasing the capacity of adsorption of various adsorbents is in the following order: qclay(15) > qTriassic sandstone(14) > qJurassic evaporates(7). Moreover, the largest adsorption capacity was found with clay due to its larger surface area (10.97 m2/g) followed by the Triassic sandstone (6.09 m2/g). The highest percentages of SiO2 group in these two-adsorbents promote a good adsorption of CO2.
Hence, the choice of an adsorbent depends on several factors such as:
-Chemical composition of the adsorbent surface;
-The textural characteristics of the adsorbent (specific surface area, pore size distribution, connected microporous...);
-The operating conditions of adsorption.
4. Conclusions
This study was devoted to comparing the CO2 adsorption by an adsorbent from El Borma field located in southern Tunisia and to selecting an efficient adsorbent suitable for storage. A thermodynamic study of CO2 adsorption on different adsorbents (Clay, Triassic sandstone, Jurassic evaporates) was performed.
The analysis of the adsorption isotherms allowed us to conclude that the isotherms are of type I according to the classification of BDDT resulting in a monolayer adsorption. In addition, the isotherms show us the absence of flat curves, indicating that the adsorption sites are not saturated in the range of the considered amount of CO2 adsorbed. The shape of the isotherms reflects a constant affinity of CO2 adsorption on different materials.
Moreover, the two-models of Langmuir and Freundlich are appropriate for describing the phenomenon of CO2 adsorption for these materials. The clay and Triassic sandstone have a higher adsorbent capacity of CO2 compared to Jurassic evaporate. Furthermore, the adsorption of CO2 on the selected material is exothermic. Indeed, the temperature affects the adsorption capacity. The number of molecules in the column at equilibrium
Table 9. Amount of carbon dioxide adsorbed on different adsorbents.
decreases with the increase of temperature. Therefore, the best adsorption capacity of carbon dioxide is obtained at low temperature.
References
- Houghton, J.T., Meira, L.G., Callender, B.A., Harris, N., Kattenberg, A. and Maskell, K. (1996) Climate Change the Science of Climate Change. IPCC (Intergovernmental Panel on Climate Change), Cambridge University Press, Cambridge.
- Ledley, T.S., Sundquist, E.T., Schwartz, S.E., Hall, D.K., Fellows, J.D. and Killeen, T.L. (1999) Climate Change and Greenhouse Gases. EOS, Transactions on American Geophysics Union, 80, 453-458. http://dx.doi.org/10.1029/99EO00325
- Roesch, A., Reddy, E.P. and Smirniotis, P.G. (2005) Parametric Study of Cs/CaO Sorbents with Respect to Simulated Flue Gas at High Temperatures. Industrial & Engineering Chemistry Research, 44, 6485-6490. http://dx.doi.org/10.1021/ie040274l
- Mosqueda, H.A., Vaquez, C., Bosch, P. and Pfeiffer, H. (2006) Chemical Sorption of Carbon Dioxide (CO2) on Lithium Oxide (Li2O). Chemistry of Materials, 18, 2307-2310. http://dx.doi.org/10.1021/cm060122b
- Wang, Y. and Levan, M.D. (2009) Adsorption Equilibrium of Carbon Dioxide and Water Vapor on Zeolites 5A and 13X and Silica Gel: Pure Components. Journal of Chemical & Engineering Data, 54, 2839-2844. http://dx.doi.org/10.1021/je800900a
- Farajzadeh, R., Farshbaf Zinati, F., Zitha, P.L.J. and Bruining, J. (2008) Density-driven Natural Convection in Dual Layered and Aniso Tropic Porous Media with Application for CO2 Injection Projects. 11th European Conference on the Mathematics of Oil Recovery (ECMOR X1), Bergen, 8-11 September 2008. http://dx.doi.org/10.3997/2214-4609.20146391
- Su, F.S., Lu, C.S., Kuo, S.-C. and Zeng, W.T. (2010) Adsorption of CO2 on Amine-Functionalized Y-Type Zeolites. Energy & Fuels, 24, 1441-1448. http://dx.doi.org/10.1021/ef901077k
- Brunauer, S. (1944) The Adsorption of Gases and Vapors. Oxford University Press, Oxford.
- Gregg, S. and Sing, K. (1982) Adsorption, Surface Area and Porosity. Academic Press, London.
- Joao, P., Bestilleiro, M., Pinto, M. and Gil, A. (2008) Selective Adsorption of Carbon Dioxide, Methane and Ethane by Porous Clays Hetero Structures. Separation and Purification Technology, 61, 161-167.
- Hengpeng, Y., Fanzhong, C., Yanqing, S., Guoying, S. and Jiamo, F. (2006) Adsorption of Phosphate from Aqueous Solution onto Modified Palygorskites. Separation and Purification Technology, 50, 283-290. http://dx.doi.org/10.1016/j.seppur.2005.12.004
- Kau, P.M.H., Smith, D.W. and Bining, P. (1997) Fluoride Retention by Kaolin Clay. Journal of Contaminant Hydrology, 28, 267-288. http://dx.doi.org/10.1016/S0169-7722(96)00081-2
- Echeverría, J.C., Morera, M.T., Mazkiarán, C. and Garrido, J. (1998) Competitive Sorption of Heavy Metal by Soils. Isotherms and Fractional Factorial Experiments. Environmental Pollution, 101, 275-284. http://dx.doi.org/10.1016/S0269-7491(98)00038-4
- Viraraghavan, T. and Kapoor, A. (1994) Adsorption of Mercury from Wastewater by Bentonite. Applied Clay Science, 9, 31-49. http://dx.doi.org/10.1016/0169-1317(94)90013-2
- Roehl, K.E. and Czurda, K. (1998) Diffusion and Solid Speciation of Cd and Pb in Clay Liners. Applied Clay Science, 12, 387-402. http://dx.doi.org/10.1016/S0169-1317(97)00022-7
- Sun, L.M. and Meunier, F. (2003) Adsorption. Aspects théoriques. Techniques de L’ingénieur, 2, 1-20.
- De Boer, J.H. (1968) Dynamical Character of Adsorption. Oxford at the Clarendon Press, Oxford.
- Julcour-Lebigue, C., Krou, N.J., Andriantsiferana, C., Wilhelm, A.M. and Delmas, H. (2012) Assessment and Modeling of a Sequential Process for Water Treatment―Adsorption and Batch CWAO Regene Ration of Activated Carbon. Industrial & Engineering Chemistry Research, 51, 8867-8874. http://dx.doi.org/10.1021/ie2020312
- Zou, Y., Mata, V. and Rodrigues, A.E. (2000) Adsorption of Carbon Dioxide on Basic Alumina at High Temperatures. Chemical Engineering Journal, 45, 1093-1095.
- Austgen, D.M., Rochelle, G.T., Peng, X. and Chen, C.C. (1989) Model of Vapor-Liquid Equilibria for Aqueous Acid Gas-Alkanolamine Systems Using the Electrolyte-NRTL Equation. Industrial & Engineering Chemistry Research, 28, 1060-1073. http://dx.doi.org/10.1021/ie00091a028
- Sang-Sup, L., Jeong-Seok, Y., Gil-Ho, M., et al. (2004) CO2 Adsorption with Attrition of Dry Sorbents in a Fuidized Bed. Preprints of Papers―American Chemical Society, Division of Fuel Chemistry, 49, 609-735.
- Mathonat, C., Majer, V., Mather, A.E. and Grolier, J.P.E. (1997) Enthalpies of Absorption and Solubility of CO2 in Aqueous Solutions of Methyldiethanolamine. Fluid Phase Equilibria, 140, 171-182. http://dx.doi.org/10.1016/S0378-3812(97)00182-9
Nomenclature
D―Flow rate [m3/h];

Vinj―injection velocity [m/s];
Tinj―Injection temperature (˚C);
T―Ambient Temperature (˚C);
q―Adsorbed amount (g/g);
qm―Maximum adsorbed amount (g/g);

KL―Constant for a given adsorbate at a particular temperature;
n―Constant for a given adsorbent at a particular temperature;
R2―Correlation Coefficient;
R―Ideal gaz constant (J.K−1∙mol−1);
ΔHads―Isosteric enthalpy of adsorption (KJ/mol);
BDDT―Brunauer, Demming & Teller Classification;
BET―Brunauer-Emmett-Teller, Measurement technique of the specific surface area of a material.



