Journal of Surface Engineered Materials and Advanced Technology
Vol.2 No.2(2012), Article ID:18806,10 pages DOI:10.4236/jsemat.2012.22016
Effects of Chemical Reaction on the Unsteady Free Convection Flow past an Infinite Vertical Permeable Moving Plate with Variable Temperature
![]()
Department of Mathematics, College of Science, Princess Norah Bint Abdulrahaman University, Riyadh, Saudi Arabia.
Email: Dr.faiza5@hotmail.com
Received December 10th, 2011; revised January 5th, 2012; accepted January 9th, 2012
Keywords: Heat and Mass Transfer; Chemical Reaction; Perturbation Technique
ABSTRACT
Analytical solutions for the effect of chemical reaction on the unsteady free convection flow past an infinite vertical permeable moving plate with variable temperature has been studied. The plate is assumed to move with a constant velocity in the direction of fluid flow. The highly nonlinear coupled differential equations governing the boundary layer flow, heat and mass transfer are solved using two-term harmonic and non-harmonic functions. The parameters that arise in the perturbation analysis are Prandtl number (thermal diffusivity), Schmidt number (mass diffusivity), Grashof number (free convection), modified Grashof number, Chemical reaction parameter (rate constant), Skin friction coefficient and Sherwood number (wall mass transfer coefficient). The study has been compared with available exact solution in the literature and they are found to be in good agreement. It is observed that: The concentration increases during generative reaction and decreases in destructive reaction. The concentration increases with decreasing Schmidt number. The effect of increasing values of K leads to a fall in velocity profiles. The velocity decreases with increasing values of the Schmidt number. An increase in modified Grashof number leads to an increase in velocity profiles. The skin friction increases with decreasing Schmidt number. In generative reaction the skin friction decreases and in destructive reaction the skin friction increases.
1. Introduction
Chemical heat and mass transfer in natural convection flows on vertical cylinders has a wide range of applications in the field of science and technology [1]. In systems where a chemical reaction of dissociation recombination takes place, the total heat transfer may be increased to the energy transfer by diffusion under the influence of a concentration gradient. Heat transfer and its related topics are heavily studied fields [2]. These studies range from over simplified problems to highly complex types of interactions and configurations which requires sophisticated numerical schemes and high speed computers to obtain reasonably accurate results [3]. However the common ground for most of these studies is that they are solved and analyzed by assuming a pure fluid with no contaminants. While this assumption approximates the reality in some cases quite well, especially for low particle contamination levels, it is not, however, valid in a lot of other cases in which the contaminants in the fluid play a major role in altering the resultant flow and heat transfer characteristics [4]. In many world environments, such as in Saudi, for example, dust storms or fine dust suspension in the air we encountered for many months during the year. These fine particles of dust penetrate the enclosures and the various devices, and have a serious impact on the performance of many equipment.
This example represents a situation of particulate suspension where a pure fluid assumption does not accurately represent the reality. The outlook for a direct coal fired magnetohydrodynamic (MHD) power generator as potentially significant source of energy seems promising in view of its efficiently, its effect on environment and the availability of needed natural resources. These studies are useful in understanding the effect of the presence of a slag layer on heat transfer characteristics of a coalfired magnetohydrodynamic (MHD) generator. A fiew representative fields of interest in which combined heat and mass transfer along with chemical reaction play an important role in chemical process industries such as food processing and polymer production. Bottemanne [1] gave the experimental results for a vertical cylinder with simultaneous heat and mass transfer and evaporation of water vapour into still air with Prandtl number (Pr = 0.71)
and Schmidt number (Sc = 0.63) under the uniform wall temperature/concentration condition. Bottemanne’s [1] experiments were conducted using a cylinder of “large diameter”. The effects of mass transfer on the flow past an impulsively started infinite vertical plate under constant heat flux condition along with chemical reaction were studied by Das et al. [2]. Exact solutions were derived by the Laplace-transformation technique. They observed that the skin friction is positive, at large values of the chemical reaction parameter. Sakiadis [3,4] studied the growth of the two dimensional velocity boundary layer over a continuously moving horizontal plate, emerging from a wide slot, at uniform velocity. Soundalgekar [5] has studied mass transfer effects on flow past an impulsively started infinite isothermal vertical plate.
Again, Soundalgekar et al. [6] analyzed the mass transfer effects on impulsively started infinite vertical plate with variable temperature or uniform heat flux. Chambre and Young [7] have studied a first order chemical reaction in the neighborhood of horizontal plate. Ramanamurthy and Govinda Rao [8] presented the results for flow past an impulsively started infinite vertical plate. They gave the detailed effects of mass transfer on the plate along with heat flux and chemical reaction. The effects of mass transfer on the flow past an impulsively started infinite vertical plate under constant heat flux condition were studied by Das et al. [9]. Ganesan and Rani [10] presented a numerical study of transient flow along a semi infinite vertical cylinder subjected to a uniform wall temperature and concentration. Ganesan and Rani [11] carried out a numerical study of transient natural convection flow over a vertical cylinder under the combined buoyancy effects of heat and mass transfer along with chemical reaction. Some works are available in the subject of MHD convection by Abdelkhalek [12-19], Benjamin Gebhart et al. [21] and Muthucumaraswany R. and Ganesan P. [22]. Unsteady MHD convection and mass transfer flow of micropolar fluid past a vertical permeable moving plate were studied by Zarea et al. [20].
It is proposed to study, the flow past an impulsively started infinite vertical plate with variable temperature and uniform mass diffusion in the presence of a homogeneous chemical reaction. The main reason for the lack of study of this problem is due to difficult mathematical and numerical procedures in dealing with the non-similar boundary layers. The highly non-linear coupled differenttial equations governing the boundary layer flow, heat and mass transfer are solved using two-term harmonic and non harmonic functions. Details of the velocities, temperature and concentration fields as well as the local skin friction and the local Sherwood number for the various values of the parameters of the problem are presented.
2. Mathematical Analysis
Consider unsteady two-dimensional flow of a laminar, viscous, and heat absorbing fluid past an infinite vertical permeable moving plate. The axial coordinate x' is measured vertically upward along the plate, and the y' axis is taken normal to the plate. At time t' ≤ 0 the plate and fluid are at the same temperature  and concentration
and concentration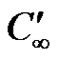 . At time
. At time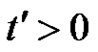 , the plate is given an impulsive motion in the vertical direction against the gravitational field with uniform velocity u0, the plate temperature is made to raise linearly with time. Also the level of the species concentration is raised to
, the plate is given an impulsive motion in the vertical direction against the gravitational field with uniform velocity u0, the plate temperature is made to raise linearly with time. Also the level of the species concentration is raised to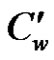 . It is also assumed that there exists a homogeneous first order chemical reaction between the fluid and species concentration. But here we assume the level of species concentration to be very low and hence heat generated during chemical reaction can be neglected. In this reaction the reactive component given off by the surface, occurs only in very dilute form. Hence, any convective mass transport to or from the surface due to a net viscous dissipation effects in the energy equation are assumed to be negligible. Under these assumptions, the boundary layer flow with Boussinesq’s approximation is governed by:
. It is also assumed that there exists a homogeneous first order chemical reaction between the fluid and species concentration. But here we assume the level of species concentration to be very low and hence heat generated during chemical reaction can be neglected. In this reaction the reactive component given off by the surface, occurs only in very dilute form. Hence, any convective mass transport to or from the surface due to a net viscous dissipation effects in the energy equation are assumed to be negligible. Under these assumptions, the boundary layer flow with Boussinesq’s approximation is governed by:
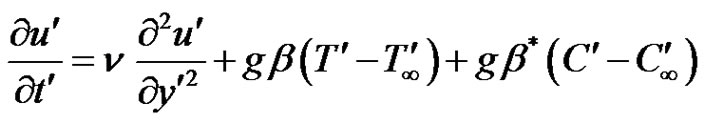 (1)
(1)
 (2)
(2)
 (3)
(3)
where, u' is the velocity of the fluid in the x' direction, g is the acceleration due to gravity, β is the volumetric coefficient of thermal expansion, β* is the volumetric coefficient of expansion with concentration, T' is the temperature of the fluid near the plate, 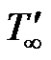 is the temperature of the fluid away from the plate,
is the temperature of the fluid away from the plate, 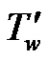 is the surface temperature t' time, t is the dimensionless time, ν is the kinematic viscosity, C' species concentration, C dimensionless species concentration,
is the surface temperature t' time, t is the dimensionless time, ν is the kinematic viscosity, C' species concentration, C dimensionless species concentration, 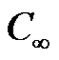 species concentration away from the plate,
species concentration away from the plate, 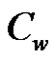 the surface species concentration, D mass diffusion coefficient, K thermal conductiveity, Kl chemical reaction parameter, ρ density of the fluid, CP specific heat at constant pressure, u dimensionless velocity, y' coordinate axis normal to the plate, y dimensionless coordinate axis normal to the plate.
the surface species concentration, D mass diffusion coefficient, K thermal conductiveity, Kl chemical reaction parameter, ρ density of the fluid, CP specific heat at constant pressure, u dimensionless velocity, y' coordinate axis normal to the plate, y dimensionless coordinate axis normal to the plate.
With the following initial and boundary conditions:
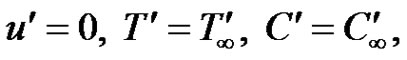 for all
for all 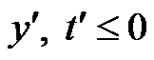
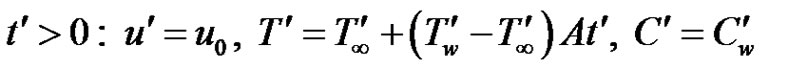 at
at 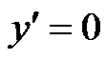
 as
as 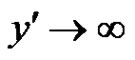 (4)
(4)
where,  , u0 velocity of the plate.
, u0 velocity of the plate.
We now introduce the following non-dimensional quantities:
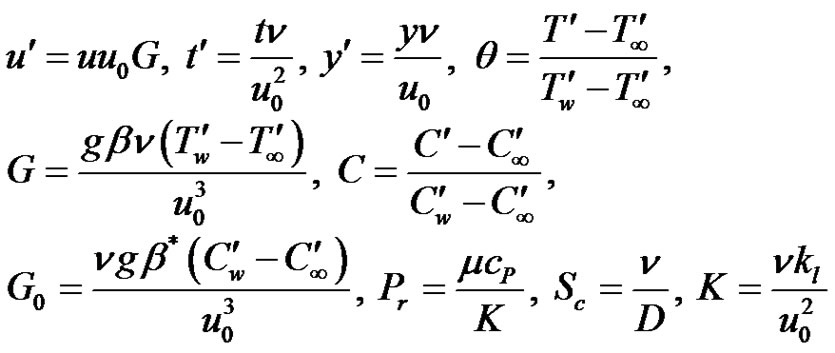 (5)
(5)
where, G Grashof number, G0 modified Grashof number, Sc Schmidt number, μ coefficient of viscosity, θ dimensionless temperature.
In Equations (1)-(4), which leads to
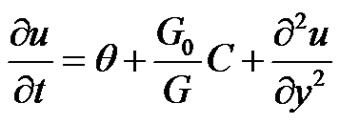 (6)
(6)
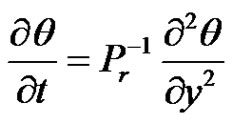 (7)
(7)
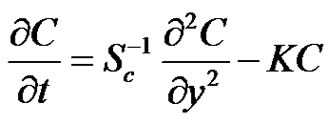
Therefore,
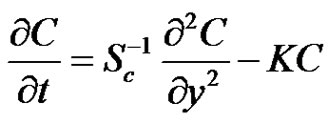 (8)
(8)
Equations (6)-(8), represent a set of partial differential equations that can not be solved in enclosed form. However, it can reduced to a set of ordinary differential equations in dimensional form that can be solved analytically, this can be done by representing the velocity, temperature and the concentration as:
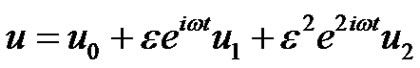 (9)
(9)
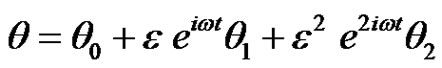 (10)
(10)
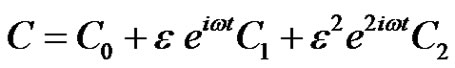 (11)
(11)
Substituting Equations (9)-(11) into Equations (6)-(8), equating the harmonic and non harmonic terms and neglecting the higher order of (ε3), and simplifying we obtain the following set of differential equations for u, θ and C.
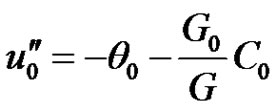 (12)
(12)
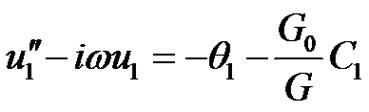 (13)
(13)
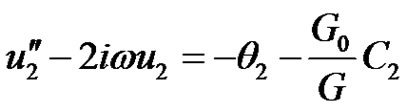 (14)
(14)
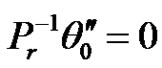 (15)
(15)
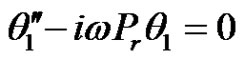 (16)
(16)
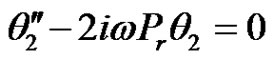 (17)
(17)
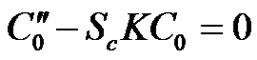 (18)
(18)
 (19)
(19)
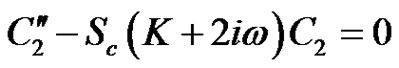 (20)
(20)
In the above equations, the primes denote differentiation with respect to y.
The boundary conditions (4) after substitution Equations (9)-(11) are reduced toat 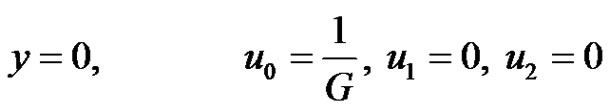
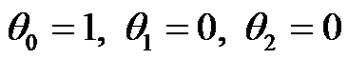

at 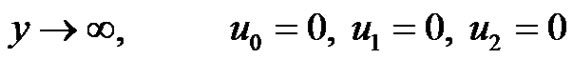
 (21)
(21)
Hence from Equations (18)-(20) under the respective boundary conditions (21), and substituting the solutions into Equation (11) the solution for concentration distribution is given by:

Also, by solving the differential Equations (15)-(17), under the boundary conditions (21), and substituting the solutions into Equation (10). We have the temperature distribution is given by:

and either from Equations (12)-(14) under the respective boundary conditions (21), and substituting the solutions into Equation (9). We have the velocity distribution.
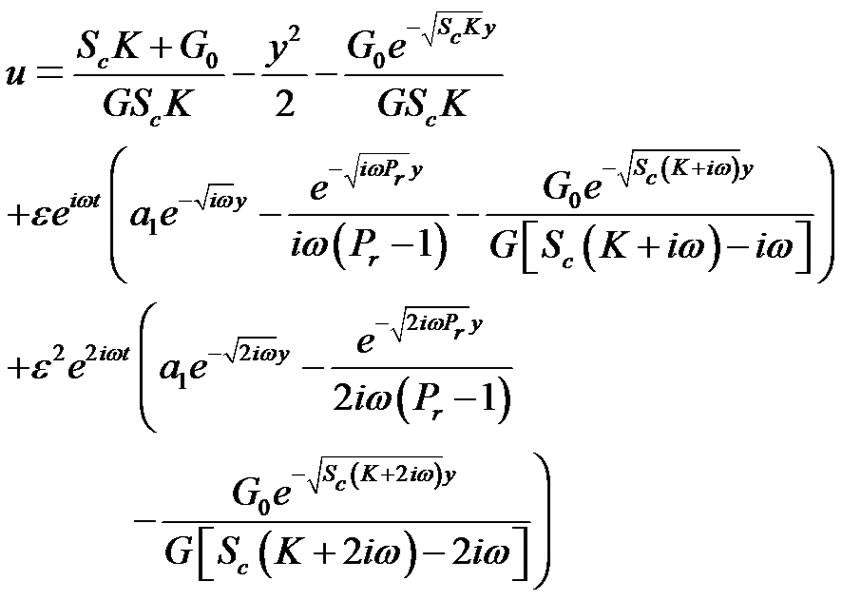
by knowing velocity, temperature, and concentration profiles, it is interesting to study about local and average values of skin friction. In non-dimensional quantities, the skin friction
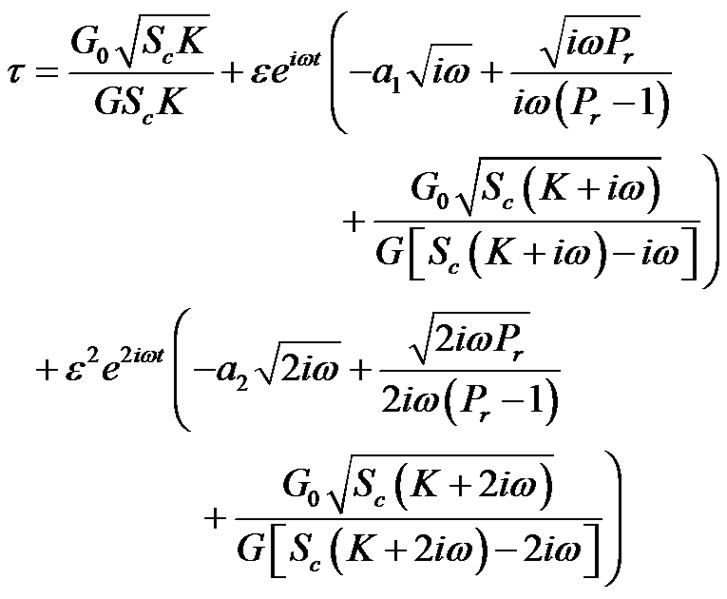
where,
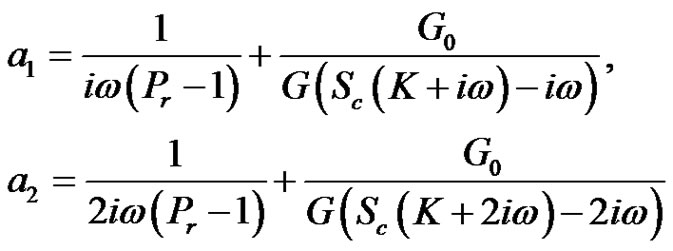
3. Results and Discussion
In order to get a physical understanding of the problem and for purpose of discussing the results, numerical calculations have been performed for the concentrationvelocity, temperature, rate of mass transfer, skin friction and rate of heat transfer. The results are represented graphically in Figures 1-10. The Prandtl number, Pr = 0.71 corresponds to air. The Grashof number, G > 0 corresponds to cooling of the plate by free convection currents, and Grashof number G < 0 corresponds to heating of the plate by free convection currents [3-6,12-19]. The mass diffusion Equation (8) can be adjusted to meet these circumstances if one takes, k > 0 for the destructive reaction, k = 0 for no reaction and k < 0 for the generative reaction. The effect of Prandtl number is very important in temperature profiles. There is a decrease in temperature due to increasing values of the Prandtl number.
The numerical values of the concentration profiles are computed and plotted in Figure 1 for different values of the chemical reaction parameter. Chemical reaction increases the rate of interfacial mass transfer. The reaction reduces the concentration. It is observed that the concentration increases during generative reaction and decreases in destructive reaction. For the case of destructive reaction increasing values of K leads to a fall in velocity profile as shown in Figure 2. A temporal maximum of velocity profiles is clearly seen for decreasing values of K. For generative reaction, a fall in velocity is observed for increasing K. This is due to the fact that as K < 0, the last term in the momentum equation becomes positive and plays a crucial role. Time required reaching steady state increases as K decreases. Here the difference between temporal velocity and steady state velocity is not clear as in the case of K > 0.
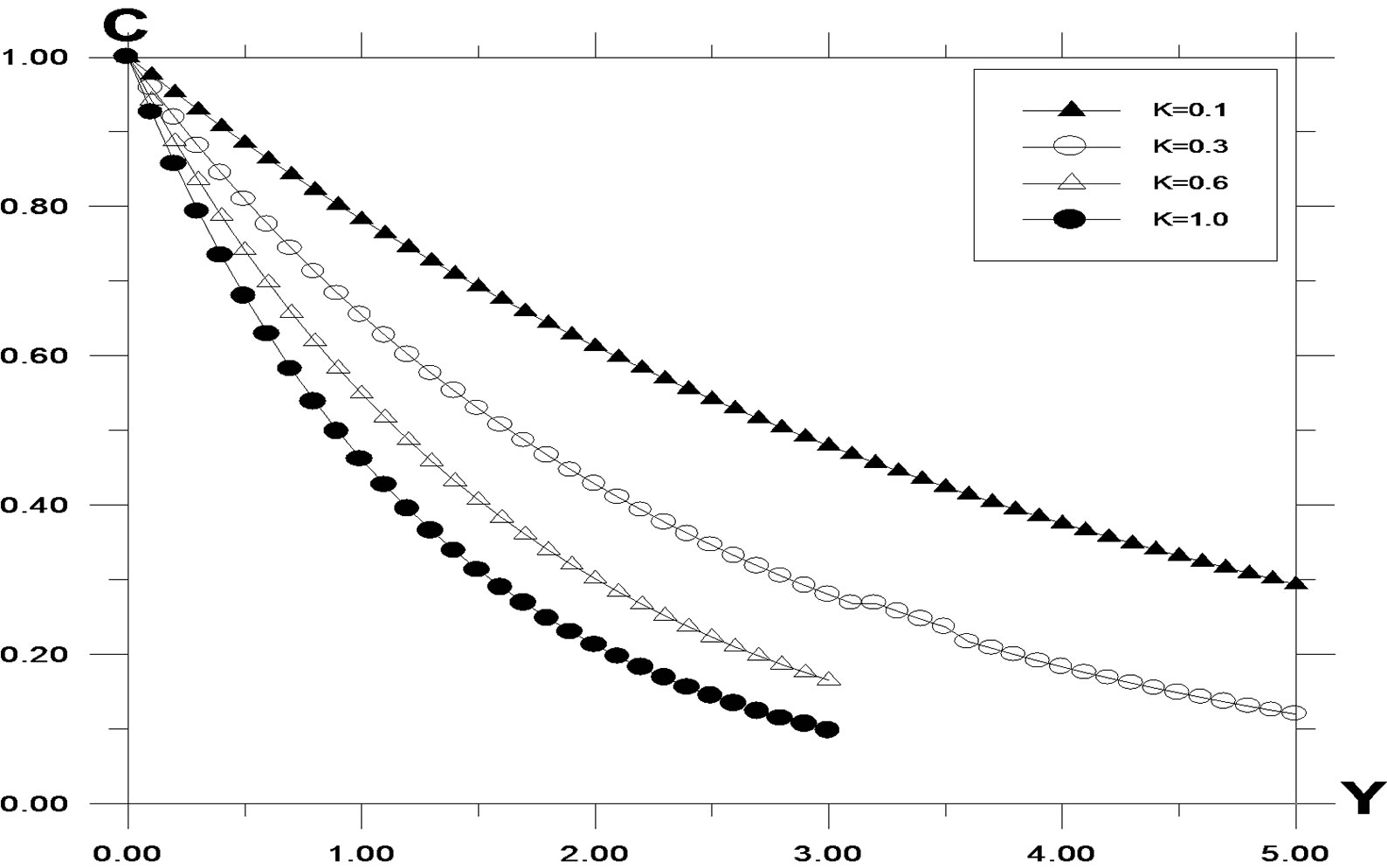
Figure 1. Concentration profile against spanwise coordinate Y for different values of K, with Pr = 0.71, t = 0.2, ω = 5.0, G = 5.0, G0 = 5.0, Sc = 0.6.
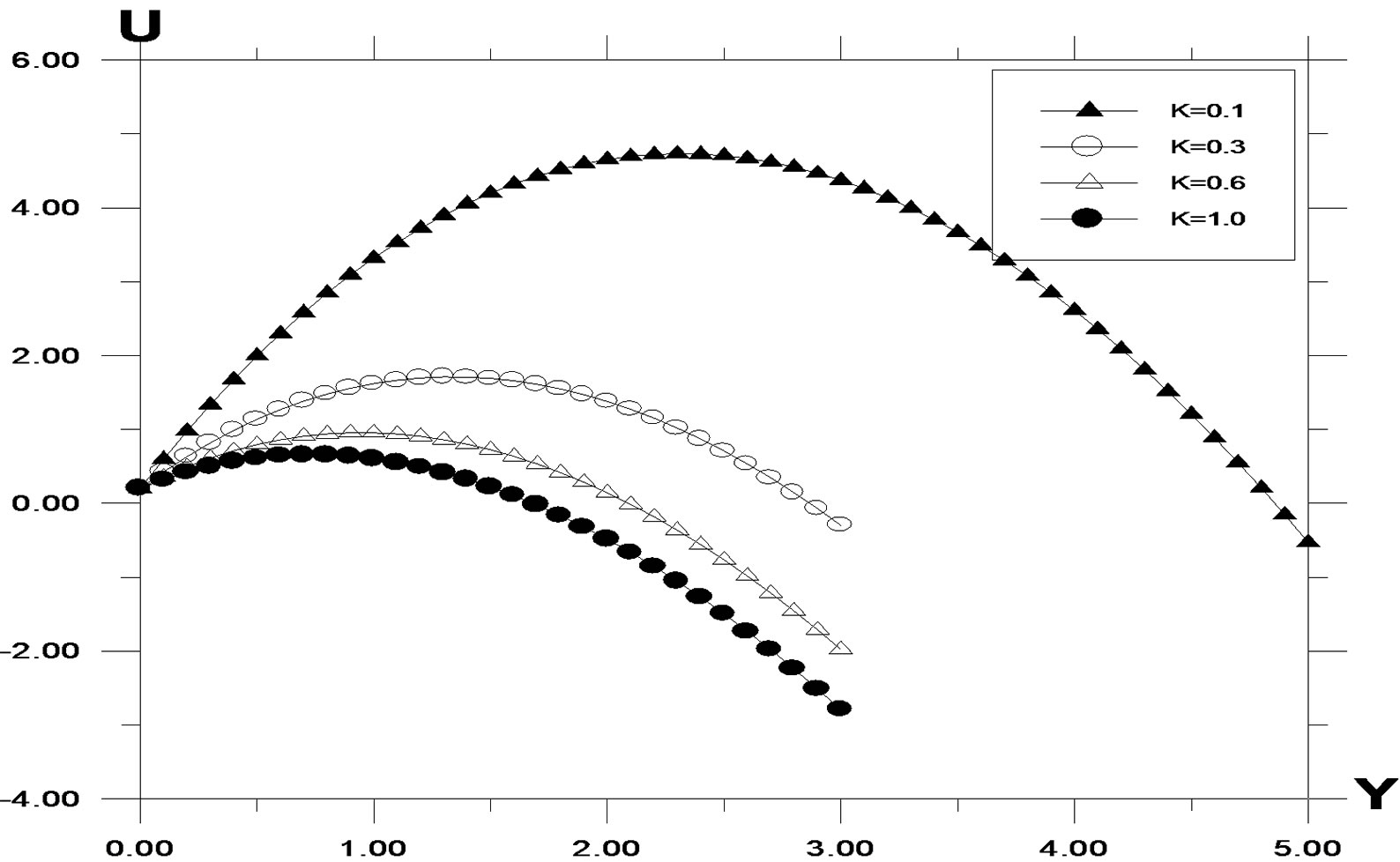
Figure 2. Velocity profile against spanwise coordinate Y for different values of K, with Pr = 0.71, t = 0.2, ω = 5.0, G = 5.0, G0 = 5.0, Sc = 0.6.
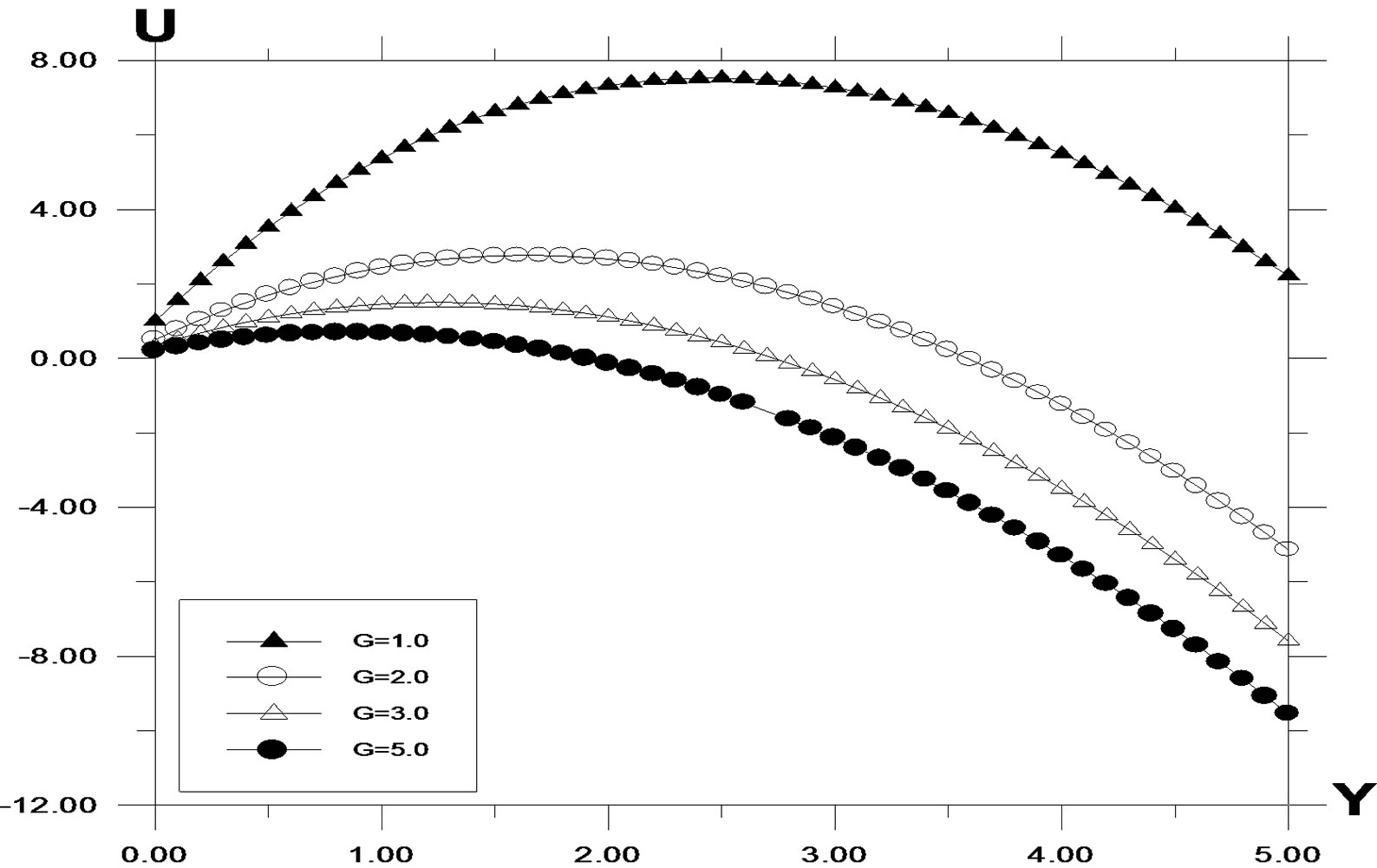
Figure 3. Velocity profile against spanwise coordinate Y for different values of Grashof number (G) with Pr = 0.71, t = 0.2, ω = 5.0, k = 0.2, G0 = 2.0, Sc = 0.6.
The velocity profiles for different values of Grashof number G are described in Figure 3. It is observed that an increase in G leads to a decrease in the values of velocity. In addition, the curves show that the peak value of velocity increases rapidly near the wall of the plate as Grashof number decreases, and then decays to the relevant free stream velocity. The velocity profiles for different values of modified Grashof number G0 are described in Figure 4. It is observed that an increase in G0 leads to a decrease in the values of velocity. In addition, the curves show that the peak value of velocity increases rapidly near the wall of the plate as modified Grashof number decreases, and then decays to the relevant free stream velocity.
The transient concentration profiles for different Schmidt number is shown in Figure 5. It is observed that the concentration increases with decreasing Schmidt number. As the Schmidt number increases, the mass transfer rate increases and hence the concentration profiles decreases. The velocity profiles for different values of Schmidt number is shown in Figure 6. It is observed that the velocity decreases with increasing values of the Schmidt number.
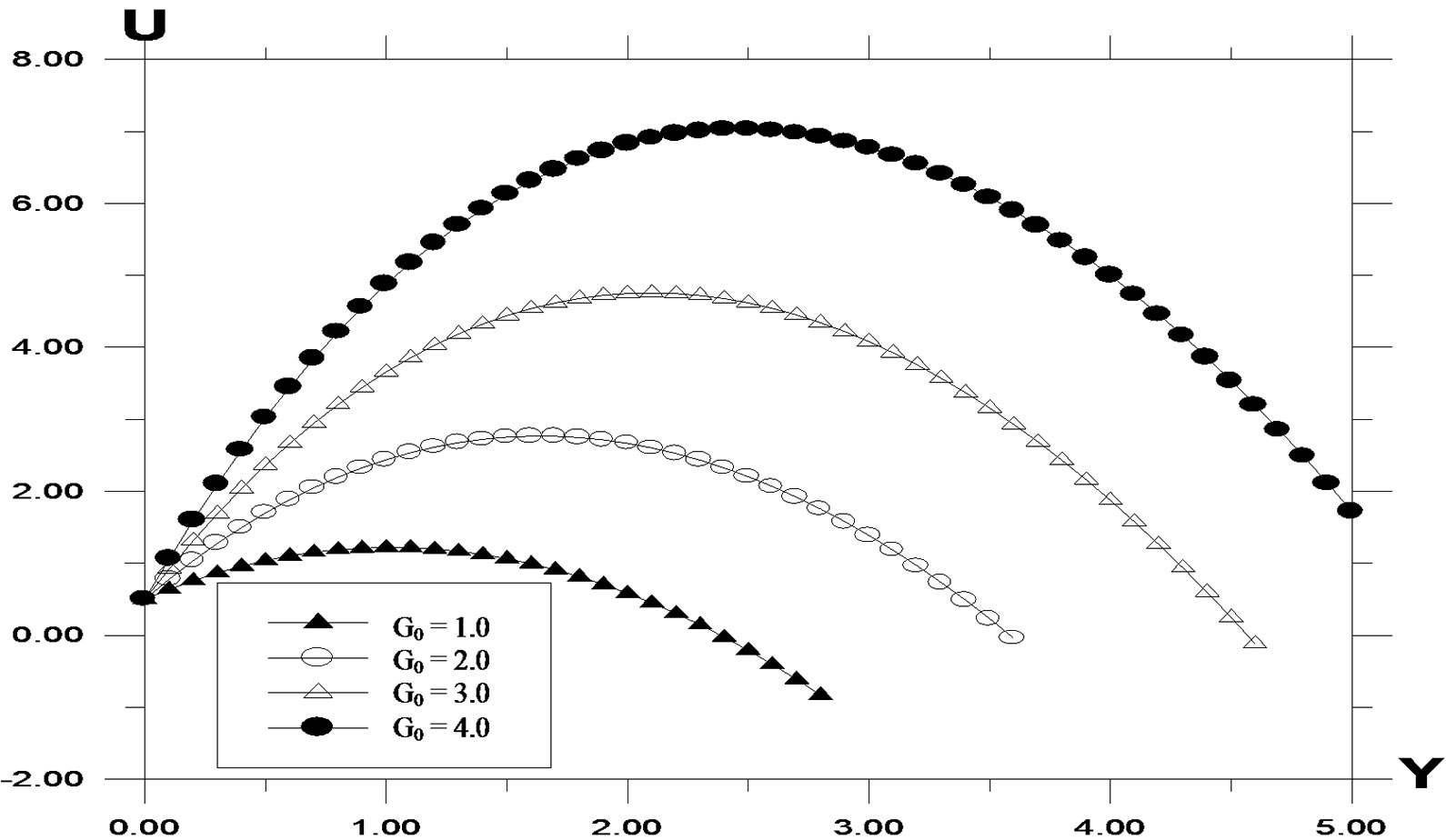
Figure 4. Velocity profile against spanwise coordinate Y for different values of modified Grashof number (G0) with Pr = 0.71, t = 0.2, ω = 5.0, k = 0.2, G = 2.0, Sc = 0.6.
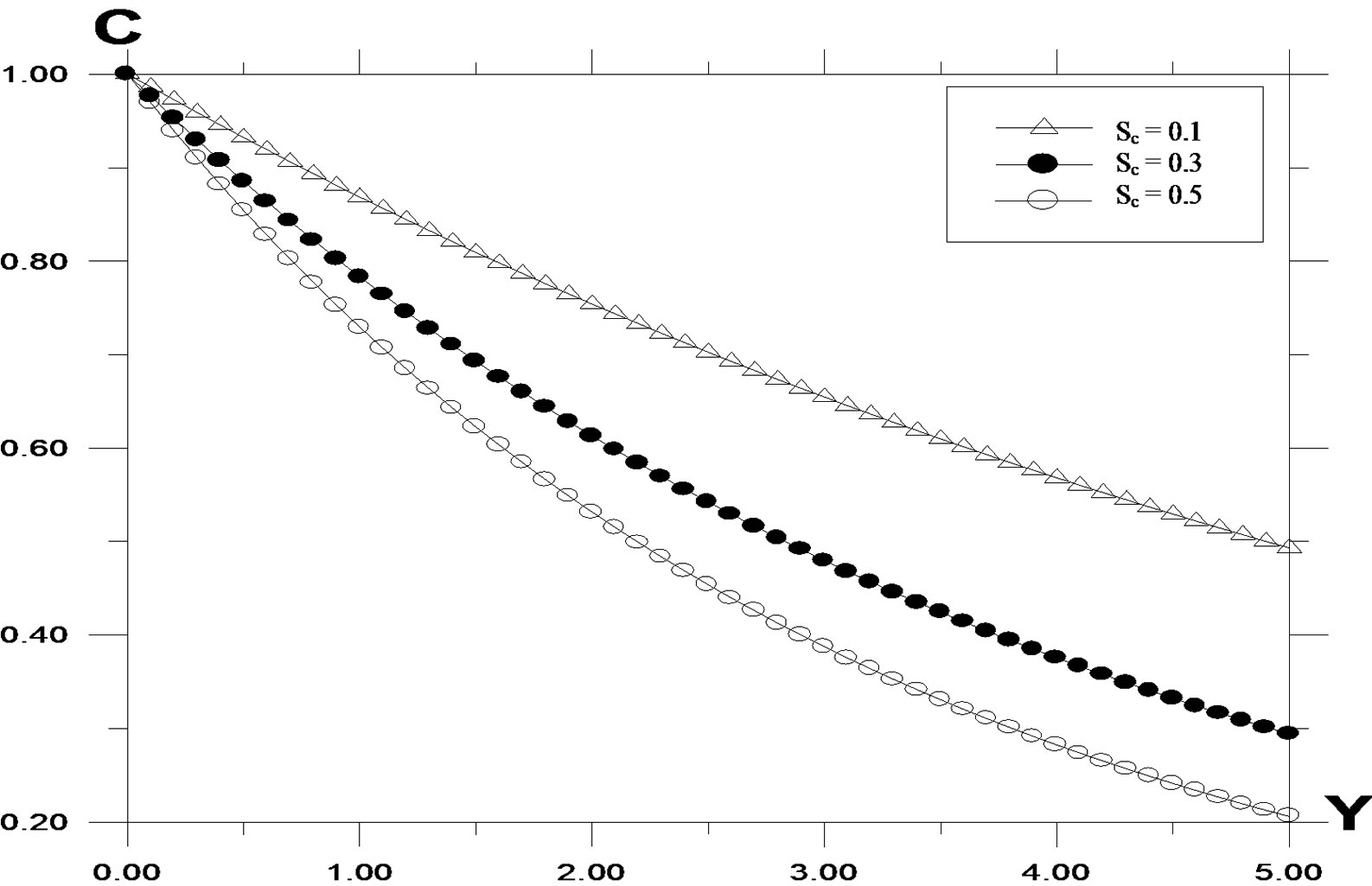
Figure 5. Concentration profile against spanwise coordinate Y for different values of Schmidt number (Sc), with Pr = 0.71, t = 0.2, ω = 5.0, G = 2.0, G0 = 2.0.
The effects of buoyancy ratio parameter for both aiding (G/G0 > 0) as well as opposing (G/G0 < 0) are shown in Figure 7. It is observed that the velocity increases in the presence of opposing flows and decreases with aiding flows. Local skin friction values are plotted in Figure 8 against the Grashof number G. They are increasing for decreasing values of Sc. Increasing values of Sc and Pr give rise to lower shear stress. Since increasing Sc and Pr gives thicker velocity profiles which in turn give lower skin friction values. As the buoyancy ratio parameter increases, higher skin friction is observed. For generative reaction, shear stress decreases as reaction parameter decreases. A similar situation is noted for destructive reaction.
Local skin friction values are plotted in Figures 9, 10 against the Grashof number G. They are increasing for
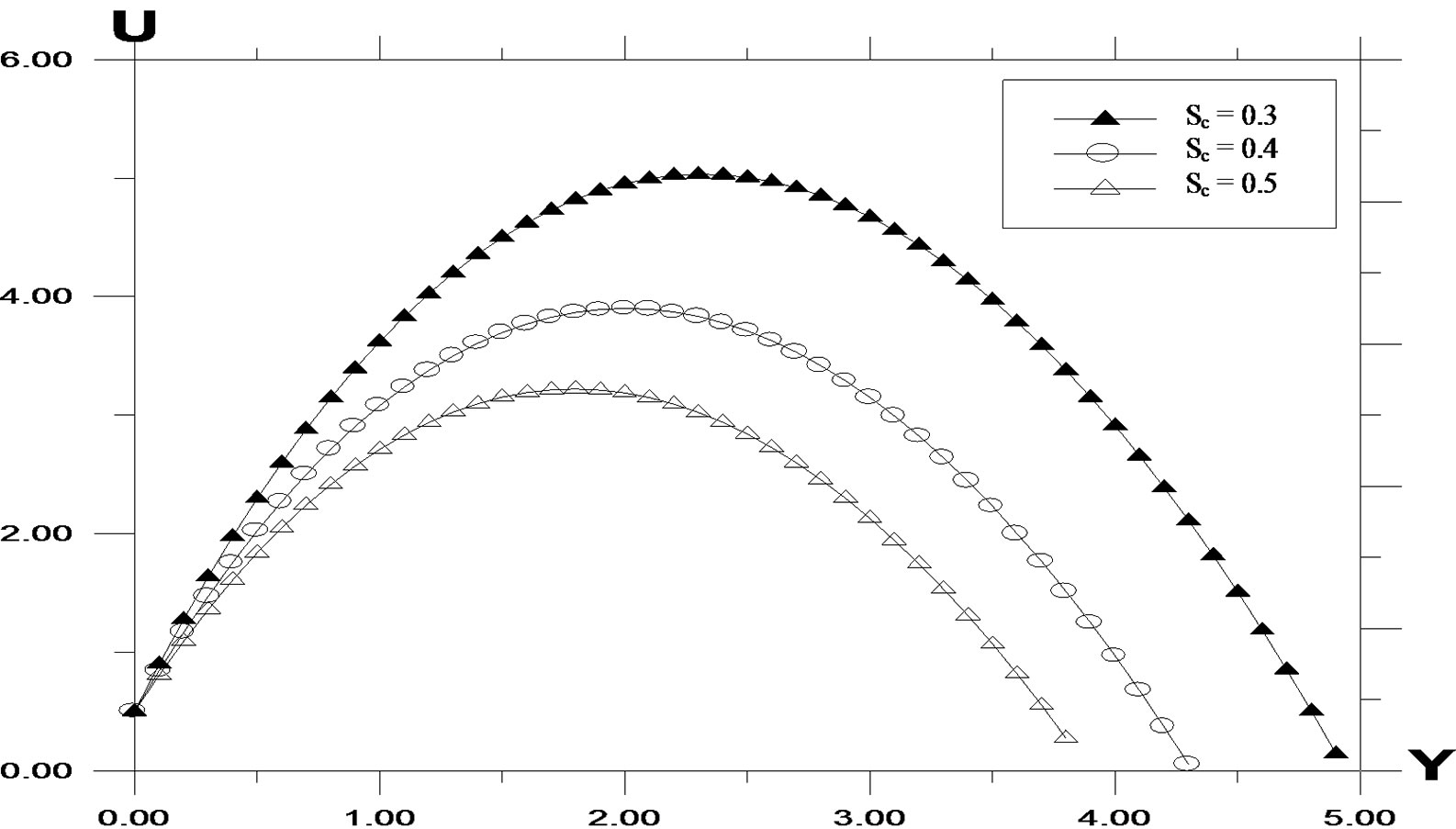
Figure 6. Velocity profile against spanwise coordinate Y for different values of Schmidt number (Sc) with Pr = 0.71, t = 0.2, ω = 5.0, k = 0.2, G = 2.0, G0 = 2.0.
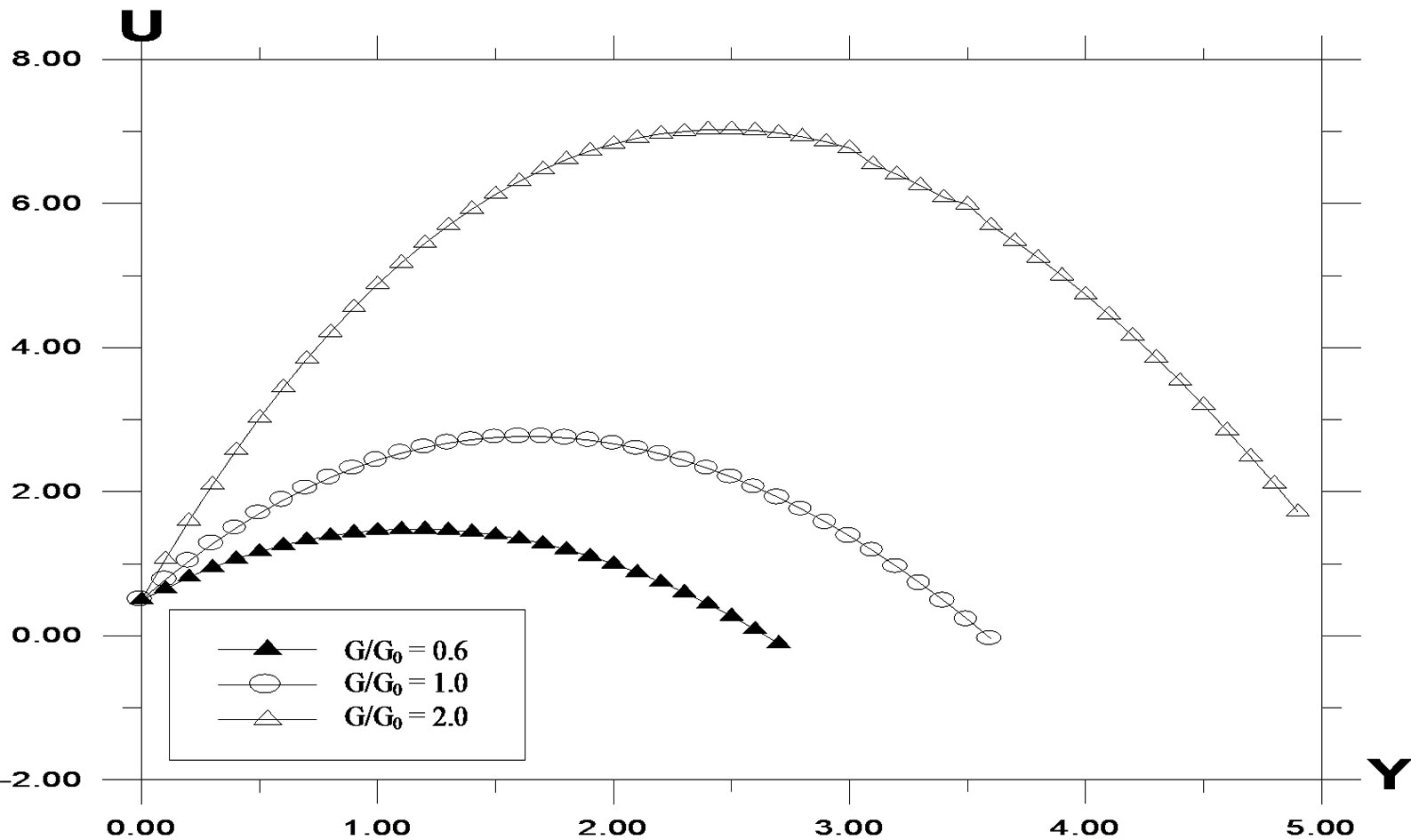
Figure 7. Velocity profile against spanwise coordinate Y for different values of (G/G0), with Pr = 0.71, t = 0.2, ω = 5.0, K = 0.2, Sc = 0.6.
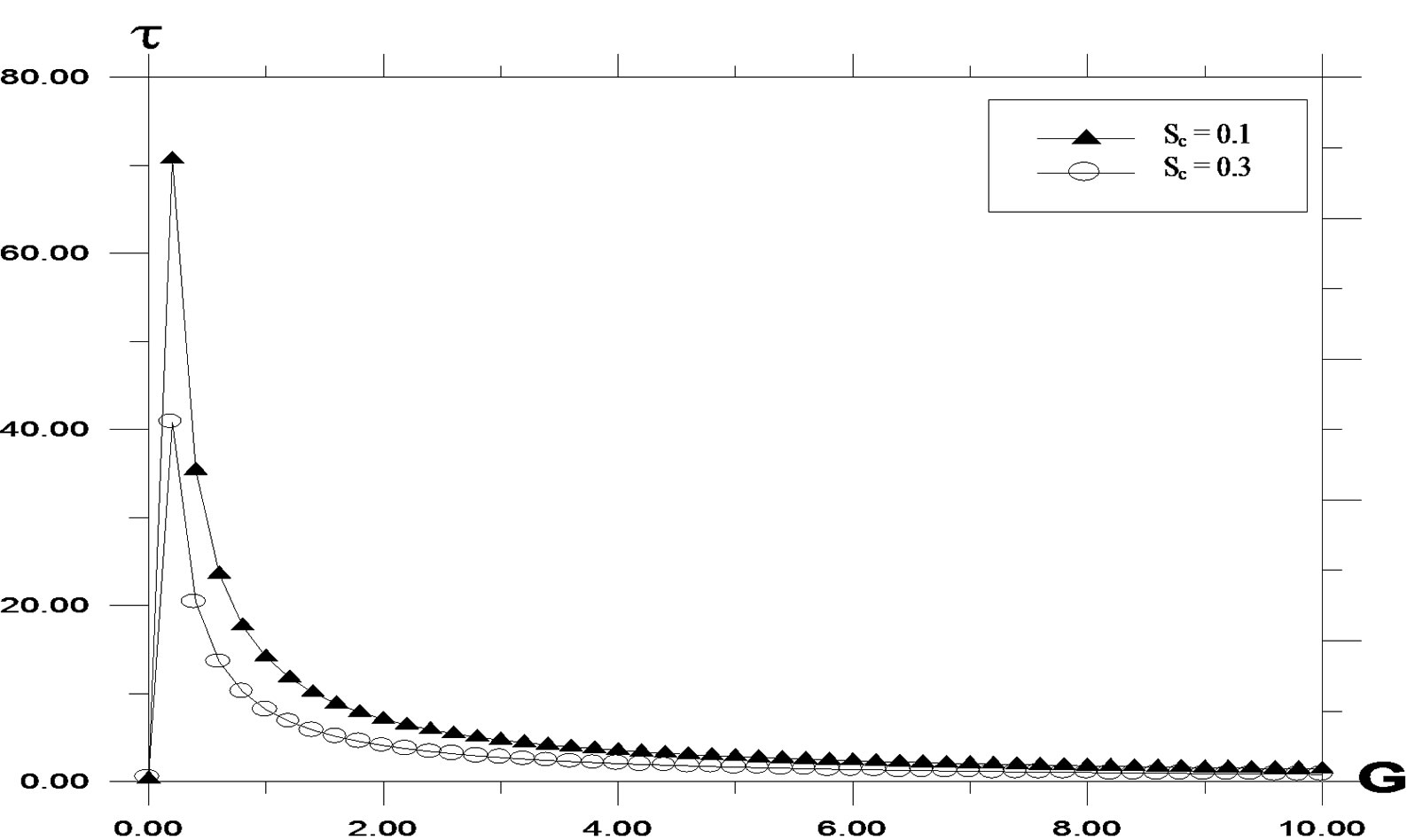
Figure 8. Skin Friction profile against Grashof number (G) for different values of Schmidt number (Sc) with Pr = 0.71, t = 0.2, ω = 5.0, K = 0.2, y = 1.
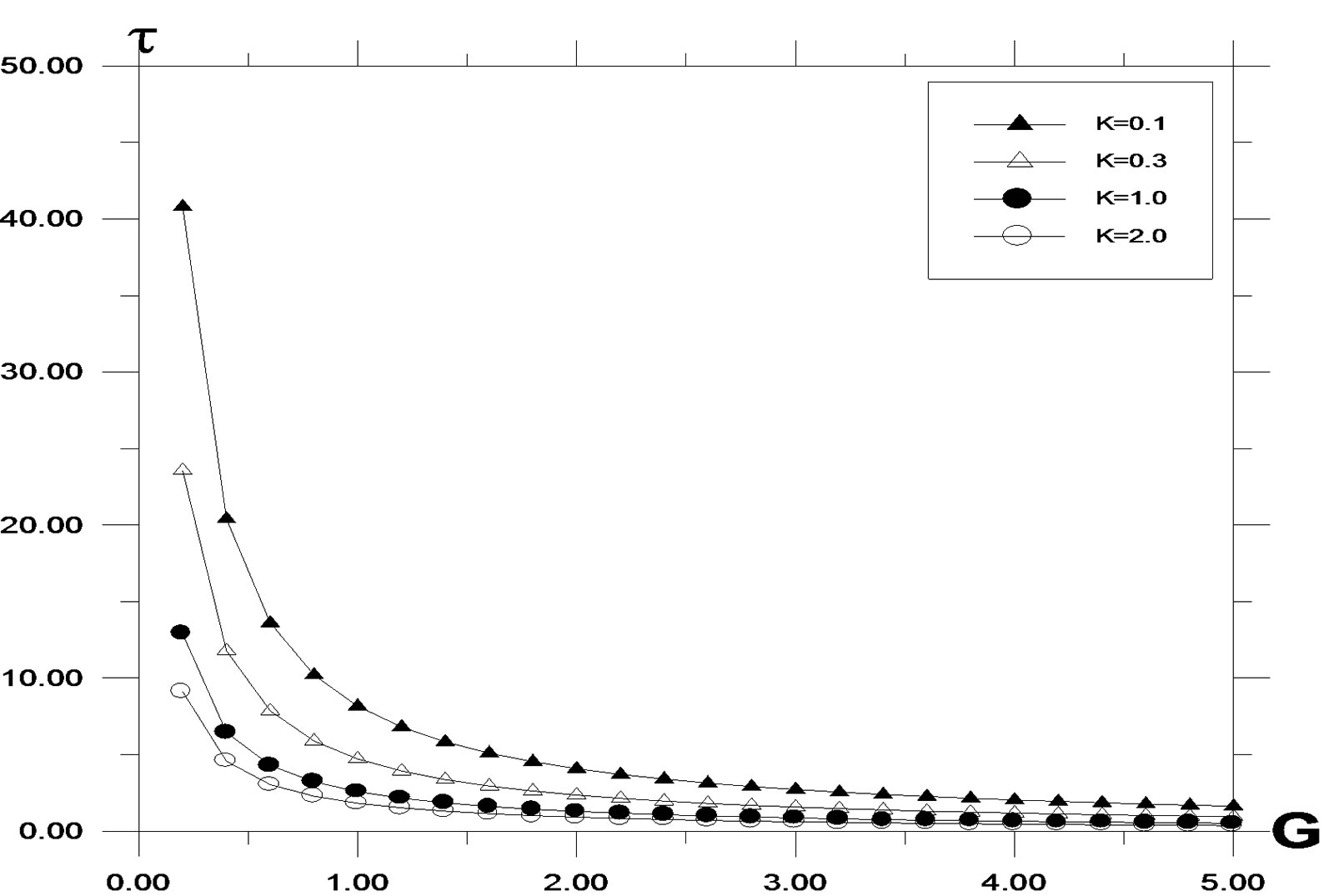
Figure 9. Skin friction profile against Grashof number (G) for different values of K, with Pr = 0.71, t = 0.2, ω = 5.0, Sc = 0.6, y = 1.0.
decreasing values of K. As the buoyancy ratio parameter increases, higher skin friction is observed. For generative reaction, shear stress decreases, as reaction parameter decreases. A similar situation is noted for destructive reaction.
4. Conclusion
A detailed numerical study has been carried out for the flow past an impulsively started infinite vertical plate with variable temperature and mass diffusion. These circumstances are of interest in several manufacturing processes.
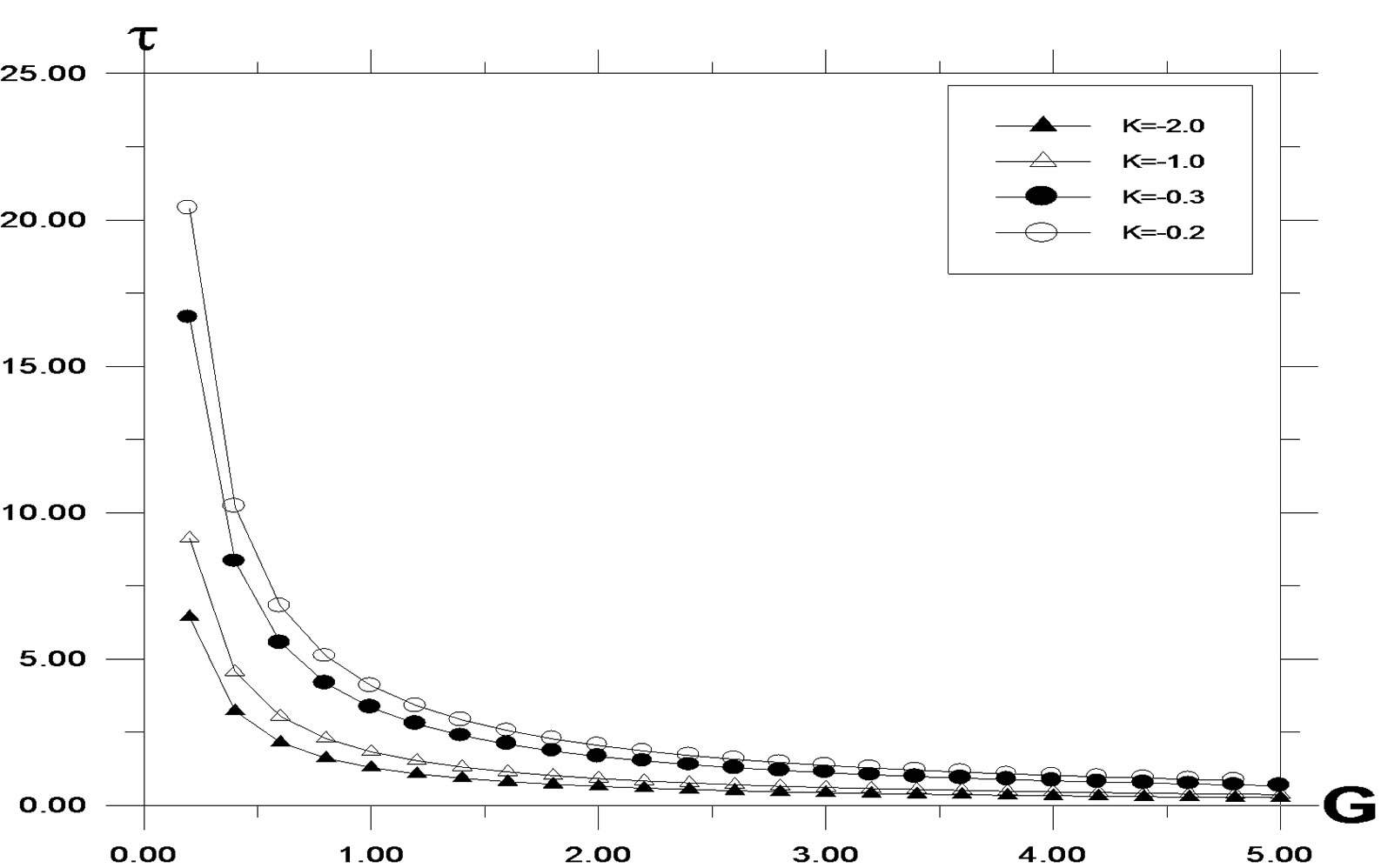
Figure 10. Skin Friction profile against modified Grashof number for different values of K, with Pr = 0.71, t = 0.2, ω = 5.0, Sc = 0.6, y = 1.0.
The dimensionless governing equations are solved by a perturbation technique. Numerical evaluations of the closed form results were performed and some graphical results were obtained to illustrate the details of the flow and heat and mass transfer characteristics and their dependence on some of physical parameters. The study has been compared with available exact solution the literature and they are found to be in good agreement. It is observed that, the concentration increases during generative reaction and decreases in destructive reaction. The concentration increases with decreasing Schmidt number. The effect of increasing values of K leads to a fall in velocity profiles. The velocity decreases with increasing values of the Schmidt number. An increase in modified Grashof number leads to an increase in velocity profiles. The skin friction increases with decreasing Schmidt number. In generative reaction the skin friction decreases and in destructive reaction the skin friction increases.
5. Acknowledgements
Appreciation is extended to the referees for their constructive and helpful comments. These led to improvements in the revised paper.
REFERENCES
- F. A. Bottemanne, “Theoretical Solution of Simultaneous Heat and Mass Transfer by Free Convection about a Vertical Flat Plate,” Applied Scientific Research, Vol. 25, No. 1, 1972, pp. 137-149. doi:10.1007/BF00382290
- T. S. Chen and C. F. Yuh, “Combined Heat and Mass Transfer in Natural Convection along a Vertical Cylinder,” International Journal of Heat and Mass Transfer, Vol. 23, No. 4, 1980, pp. 451-461. doi:10.1016/0017-9310(80)90094-0
- B. C. Sakiadis, “Boundary-Layer Behavior on Continuous Solid Surfaces: I. Boundary-Layer Equations for TwoDimensional and Axisymmetric Flow,” AIChE Journal, Vol. 7, No. 1, 1961, pp. 26-28. doi:10.1002/aic.690070108
- B. C. Sakiadis, “Boundary-Layer Behavior on Continuous Solid Surfaces: II. The Boundary Layer on a Continuous Flat Surface,” AIChE Journal, Vol. 7, No. 1, 1961, pp. 221-225. doi:10.1002/aic.690070211
- V. M. Soundalgekar, “Effects of Mass Transfer and FreeConvection Currents on the Flow past an Impulsively Started Vertical Plate,” Journal of Applied Mechanics, Vol. 46, No. 4, 1979, pp. 757-760. doi:10.1115/1.3424649
- V. M. Soundalgekar, N. S. Birajdar and V. K. Darwhekar, “Mass-Transfer Effects on the Flow past an Impulsively Started Infinite Vertical Plate with Variable Temperature or Constant Heat Flux,” Astrophysics and Space Science, Vol. 100, No. 1-2, 1984, pp. 159-164. doi:10.1007/BF00651593
- P. L. Chambre and J. D. Young, “On the Diffusion of a Chemically Reactive Species in a Laminar Boundary Layer Flow,” Physics of Fluids, Vol. 1, 1958, pp. 48-54. doi:10.1063/1.1724336
- K. V. Ramanamurthy and V. M. Govinda Rao, Proceedings of the First National Heat and Mass Transfer Conference, Chennai, 1971.
- U. N. Das, R. Deka and V. M. Soundalgekar, “Effects of Mass Transfer on Flow past an Impulsively Started Infinite Vertical Plate with Constant Heat Flux and Chemical Reaction,” Forschung im Ingenieurwesen, Vol. 60, No. 10, 1994, pp. 284-287. doi:10.1007/BF02601318
- P. Ganesan and H. P. Rani, “Transient Natural Convection along Vertical Cylinder with Heat and Mass Transfer,” Heat and Mass Transfer, Vol. 33, No. 5-6, 1998, pp. 449-455. doi:10.1007/s002310050214
- P. Ganesan and H. P. Rani, “On Diffusion of Chemically Reactive Species in Convective Flow along a Vertical Cylinder,” Chemical Engineering and Processing, Vol. 39, No. 2, 2000, pp. 93-105. doi:10.1016/S0255-2701(99)00018-5
- M. M. Abdelkhalek, “The Skin Friction in the MHD Mixed Convection Stagnation Point with Mass Transfer,” International Communications in Heat and Mass Transfer, Vol. 33, No. 2, 2006, pp. 248-257. doi:10.1016/j.icheatmasstransfer.2005.09.008
- M. M. Abdelkhalek, “Mixed Convection in a Square Cavity by a Perturbation Technique,” Computational Materials Science, Vol. 42, No. 2, 2008, pp. 212-219. doi:10.1016/j.commatsci.2007.07.004
- M. M. Abdelkhalek, “Hydromagnetic Stagnation Point Flow by a Perturbation Technique,” Computational Materials Science, Vol. 42, No. 3, 2008, pp. 497-503. doi:10.1016/j.commatsci.2007.08.013
- M. M. Abdelkhalek, “Heat and Mass Transfer in MHD Flow by Perturbation Technique,” Computational Materials Science, Vol. 43, No. 2, 2008, pp. 384-391. doi:10.1016/j.commatsci.2007.12.003
- M. M. Abdelkhalek, “Unsteady MHD Convection and Mass Transfer Flow of Micropolar Fluids past a Vertical Permeable Moving Plate with heat Absorption,” Indian Journal of Physics, Vol. 80, No. 6, 2006, pp. 625-635.
- M. M. Abdelkhalek, “Thermal Radiation Effects on Hydromagnetic Flow,” Computer Assisted Mechanics and Engineering Sciences, Vol. 14, No. 3, 2007, pp. 471-484.
- M. M. Abdelkhalek, “Radiation and Dissipation Effect on Unsteady MHD Micropolar Flow past an Infinite Vertical Plate in a Porous Medium with Time Dependent Suction,” Indian Journal of Physics, Vol. 82, No. 4, 2008, pp. 415-434.
- M. M. Abdelkhalek, “Heat and Mass Transfer in MHD Free Convection from a Moving Permeable Vertical Surface by a Perturbation Technique,” Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 5, 2009, pp. 2091-2102. doi:10.1016/j.cnsns.2008.06.001
- S. A. Zarea, F. M. El-Fayez and M. M. A. Khalek, “Perturbation Technique Algorithm for Mixed Convection Flow in a Confined Saturated Porous Medium with Temperature,” Arab Journal of Nuclear Sciences and Applications, Accepted, 2010.
- B. Gebhart, Y. Jaluria, R. L. Mahajan and B. Sammakia, “Buoyancy-Induced Flows and Transport,” Hemisphere Publishing Corporation, New York, 1988.
- R. Muthucumaraswany and P. Ganesan, “Diffusion and First-Order Chemical Reaction on Impulsively Started infinite Vertical Plate with Variable Temperature,” International Journal of Thermal Science, Vol. 41, No. 5, 2002, pp. 475-479.

