ABSTRACT

Enhancement of the Human Immunodeficiency Virus (HIV) specific cytotoxic T- cells mechanisms in an HIV-1 and Mycobacterium tuberculosis (Mtb) co-infected individual seems to improve the clinical picture of an individual by reducing Acquired Immuno Deficiency Syndrome (AIDS) state progression rate. In this paper, we develop a system of deterministic differential equations representing the immune cells involved in an HIV-1 and Mtb co-infected individual. Results show that although the non-lytic arm of the HIV-1 cytotoxic T-cells affects the co-infection dynamics more than the lytic factors, a combination of both factors results in a more positive reduced progression to the AIDS state. This is due to the increased protection of the CD4⁺ T-cells by the CTL mechanisms by further reducing infections and replications by the HIV. Thus, HIV-1 specific CTLs mechanisms’ involvement is here recommended to be part of a solution to the HIV and Mtb co-infection problems.

Keywords:

Mycobacterium tuberculosis, HIV, Co-Infection, Cytotoxic T-Cells, Lytic and Non-Lytic Factors

1. Introduction

1.1. HIV and Mycobacterium tuberculosis (Mtb) Co-Infection

Since the resurgence of HIV, Mtb and HIV has been closely linked, the HIV-1, Mtb co-infection causes a two-infection disease endangering human immune response which may also differ depending on the genetic background [1] . Approximately one- third of the world’s population is latently infected with Mtb [2] . The rate of progression from infection to full blown disease varies greatly with at least 10% of Mtb infected individuals developing clinical disease and about half of them developing disease more than two years after infection, commonly named reactivation or post-primary TB [3] . Thus, the lifetime risk of developing active TB in immunocompetent adults is estimated to be 5% - 10%, but in HIV-positive individuals this risk is increased to 5% - 15% annually [4] . The depletion of CD4⁺ T-cells, which is a main feature of AIDS, is certainly an important contributor to the increased risk of reactivation of latent TB and susceptibility to new Mtb infection. HIV also manipulates macrophage bactericidal pathways [5] , deregulates chemotaxis [6] , and tips Th1/Th2 balance [7] and may impair Tumor Necrosis Factor (TNF)-mediated macrophage apoptotic response to Mtb and thus facilitates bacterial survival [8] . Specifically, TB patients with AIDS present a dominant granulocytic infiltrate and necrosis without the typical necrosis seen in non- HIV-infected TB granulomas due to the killing of CD4⁺ T-cells in the granuloma by the HIV [9] .

HIV produces a progressive decline in the cell mediated immunity by virtue of the pathogen targeting the CD4⁺ T-cells eventually disabling them and making them dysfunctional. The decline impacts negatively on the control of the Mtb by the immune system since the CD4⁺ T-cells are also needed for the cell immune mediated response for the Mtb infection to keep TB in check. HIV also alters the pathogenesis of TB, greatly increasing the risk of developing active disease in a co-infected individual leading to more extra pulmonary involvement and radiographic manifestations.

The function of many immune cells, including macrophages and Dendritic cells (DCs), is modulated by both HIV and Mtb, with the presence of Mtb increasing replication of the virus in a co-infected individual [10] . Mtb has been reported to up-regu- late HIV-1 replication in chronically or acutely infected T-cells or macrophages [11] [12] . The primary target for Mtb, the alveolar macrophage, can also be infected with HIV exacerbating HIV replication in macrophages and lung cells obtained by bronchoalveolar lavage from co-infected individuals [10] [12] [13] . In-vitro Mtb infection can up-regulate both HIV infection and replication within monocyte-derived macrophages (MDMs), increase the efficiency of virus transmission from infected MDMs to T-cells, and favor replication of X4 HIV variants by upregulation of CXCR4 [14] . It is therefore evident that the presence of each of these diseases has a profound effect on the other due to the interactions with the immune system. This is because the frequency at which HIV and Mtb occurs together is determined by the epidemiology of each of the disease in a given population. Thus, co-infection has also become one of the main complications worldwide with TB being the cause of death for one out of every three people with AIDS.

1.2. Why Cytotoxic Cells?

The challenges that the world is facing in HIV and Mtb co-infection can possibly be solved through a combined vaccine. However, design of candidate vaccines is a parti- cularly difficult task since laboratory correlates of protection have not been defined for Mtb and HIV infections. Vaccination efforts have shown that Mtb infection diminish HIV-specific Immunoglobulin A (IgA) responses at mucosal surfaces which help prevent HIV infection or reduce the viral load [15] . In addition, vaccine-induced immune responses need to be tipped towards protection, avoiding those that may result in immunopathology, this requires meticulous study of appropriate adjuvants, antigens, and vaccination regimens for the novel vaccines [16] . Even with treatment, it has been noted with serious concern regarding current recommendations for treatment of HIV- Mtb co-infection since data suggest that at least 8 months duration of rifapentine (RPT), or rifampin (RIF) therapy, initial daily dosing, and concurrent antiretroviral therapy might be associated with better outcomes, but adequately powered randomized trials are urgently needed to confirm [17] . The criteria for deciding between strategies to treat a co-infected individual still remains a challenge although a more robust quan- titative measure could help by incorporating rate of change of CD4⁺ count as a measure of Integrated Risk Information System (IRIS) risk, as well as viral and bacterial load, drug toxicity, and improved measures of drug interaction [18] . The presence of the CTLs cannot be sidelined in an effort to come up with solutions to HIV-Mtb co- infections. Studies have shown that the presence of Mtb affect the C38 expression on the CD8⁺ cells responsible for CTL differentiation. This negatively impacts the HIV progression which may also depend on the ethnic group (genes) [19] . There have been several hypotheses set regarding the relationship between HIV specific CTLs and viral load. The findings strongly support the involvement of CTLs in the control of HIV infection [20] but does it have the same effect in the case of co-infection? The CD8⁺ cellular responses like CTLs are potential mediators of protection against HIV [21] .

Understanding the vital effects of Cytotoxic T-cells as an immune system component might be of paramount importance for vaccine development. The tropism of the co-infection between HIV-1, Mtb and the immune system studied by Kirshner [22] can be bridged by including the role of the Cytotoxic T-cells (CTLs: a special type of the CD8⁺ T-cells) in the immune system. CTLs play an important role in controlling both HIV and Mtb. This is made possible by incorporating the lytic and non-lytic responses of the CTLs. The lytic response involves the destruction of infected T-cells by the effector cells. The CTLs are antigen specific as they possess receptor molecules on their surface that can recognise the antigen epitope (portion of antigen which which specifically interacts with the immune system). These receptors are designed in such a way that they recognise antigen only when they are bound to a cell surface molecule called the major histocompatibility complex (MHC). The MHC presents peptides to CTLs which then destroy the infected cell if it can bind the peptide-MHC class1 complex [23] . In a co-infected individual, the CTLs are responsible for killing infected T-cells by both HIV and Mtb. This is made possible when naive CD8⁺ T-cells are converted into CTLs which are either HIV specific CTLs or Mtb specific CTLs through the B-cells. The CTLs are essential in many ways in the control of Mtb infection through their different effector mechanisms including activation of macrophages when they induce the release of the Interferon gamma (INF-) thereby by activating infected macrophages to induce reactive nitrogen intermediates [24] . They also mediate lysis of infected macrophages through the Fas-FasL pathway predominantly achieved by the CD4⁺ T-cells and through the granule exocytosis pathway [24] . CTLs also induce target cell apoptosis and kill the bacteria directly by the granulysin which result in the alteration of bacterial cell membrane.

In this paper, we focus on the HIV specific CTLs only and how they help to reduce the two infection disease progression. Non-lytic response of the CTLs involves the prevention of infection of new cells and inhibition of replication by soluble mediators secreted by the immune system. The CTLs then caters for the non-lytic response by producing chemokines like the 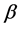-chemokine that helps to reduce viral load at the early stages of the HIV infection (the asymptomatic stage) as they block the entry of virions into the CD4⁺ T-cells [25] . They also produce cytokines. The HIV specific CTLs principally produce the INF-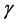, Interleukin-6 (IL-6) and Interleukin-10 (IL-10) which suppress the rate of viral production [26] . The INF- 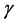cytokines produced by the CTLs are also responsible for the activation of the macrophages so that they clear the Mtb bacteria and the HIV virus. Although we are not going to incorporate the Mtb specific CTLs, it should be noted that they also produce the INF- 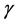cytokine and the TNF which again are responsible for the inhibition of new infection by the Mtb. We will also consider the dynamics looked at by Kirshner [22] and incorporate the HIV specific CTLs mechanisms in the immune system and propose a mathematical model describ- ing the dynamics of uninfected T-cells, virally infected CD4⁺ T-cells, macrophages, HIV pathogen, Mtb pathogen and the HIV specific CTLs with the immune system.

2. Model Formulation

The model by Kirshner [22] is here introduced and used as our basic model. This model focuses on the study of the hypothesis that the presence of infection of HIV with Mtb in the body worsens the clinical picture of HIV and that the presence of HIV can activate the Mtb infection. This was done incorporating the interactions of the immune system's key players which include the lymphocytes or T-cells, macrophages, HIV and Mtb. Four population groups of cells and pathogens are here used namely: the armed CD4⁺ and CD8⁺ T-cell population at time 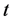represented by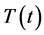, the macrophage population at a given time represented by, the HIV population is represented by 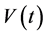and the Mtb population at a time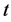, represented by. The model is explained in detail in [22] . The following system of equations were proposed:

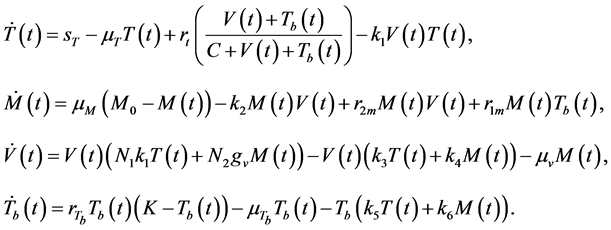(1)

The interactions of both pathogens with the immune system are explored in [22] using system (1) and results show that the T-cells population is lower in the presence of both pathogens than in the case of HIV alone. The results also showed that viral load is higher in a co-infected patient than in a single infected patient and the same trend was observed for the Mtb. Thus, since progression to AIDS is based on the CD4⁺ T-cell count and the viral load, the presence of Mtb in an HIV infected individual worsens the clinical picture of the AIDS state.

Model with CTL Mechanisms

The lytic and non-lytic factors of the HIV specific CTLs are here incorporated to system (1), in order to analyse their effects to the dynamics of disease progression in a co-infected individual. In particular, HIV specific CTL T-cells response in HIV infection and its effects to the whole immune system dynamics. Thus CTLs are here modelled with their HIV specific function and not just as general T-cells as done by [27] and by monitoring the dynamics of six groups of population cell densities: the population density for the uninfected T-cells at a time 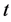(a pool of the CD4⁺ T-cells, Mtb specific CTLs and naive CD8⁺ T-cells)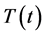; the virally infected CD4⁺ T-cells at a time,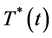; the free viral particles population at a time,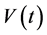; the density of the resting, activated and infected macrophages,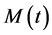; the population density of the Mtb pathogen at a time, 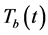and the density of the HIV-1 specific CTLs population at a time,. We also assumed that the immune cells proliferation has different limit values since their production is controlled by the source from which they are coming from either the thymus for the CD4⁺ T-cells and the CD8⁺ T-cells and the bone marrow for the macrophages. Proliferation of cells is treated differently in the model depending on whether infection is by the virus or the Mtb bacteria.

Uninfected CD4⁺ T-cells are produced from the thymus at a rate of and die naturally at a rate. Proliferation of the T-cells due to infection by both the Mtb and

HIV pathogens are modelled by the factors and respec-

tively, where are maximum proliferation rates and are parameters that determine the amount of pathogen needed for half maximum stimulation of CD4⁺ T-cells by the Mtb and HIV respectively [22] . Parameter represents the apoptotis with being the level of apoptotic engagement by the receptors [27] . Infection of the CD4⁺ T-cells and the macrophages by HIV occurs at rates and, respectively, with the infection haboured due to the presence of the CTLs by a factor of

, where is the efficiency of each CTL in reducing CD4⁺ T-cell in-

fection [27] . Infected CD4⁺ T-cells are also directly killed by the CTLs at a rate and lost due to bursting and natural death at a rate of releasing and virions from the infected CD4⁺ T-cells and macrophages, respectively. Again, this viral replication is limited due to the presence of the CTLs as they produce chemokines by a

factor of, where is the rate at which CTLs suppresses viral pro-

duction. Macrophage proliferation due to infection by the HIV and Mtb are modeled at the rates and, respectively. Mtb pathogen can also be eliminated from the system by phagocytosis action of Mtb specific CTLs (here just considered as T-cells) at a rate or by the macrophages at rate. The logistic growth rate of the Mtb bacteria is accounted for by, where as carrying capacity and the pathogen dies naturally at a rate of. The macrophages natural death rate is represented by. Finally, the HIV-1 cytotoxic T-cells themselves are produced from the source of HIV specific CTLs [28] [29] . The source represent the new CD8⁺ T-cells from the thymus and those from the precursors. The naive CD8⁺ T-cells are then differentiated into HIV specific CTLs which can also proliferate at rate due to infection by the HIV. A process dependent on the help by the CD4⁺ T-cells and antigen present from the B-cells [28] [29] . The CTLs can also die naturaly at a rate. Thus these immune dynamics facts can be represented by the following system of equations:

(2)

3. Initial Conditions and Reproductive Number, R₀

3.1. Disease Free State (E₀)

The disease free equilibrium is given by where the abundance of the uninfected CD4⁺ T-cells, infected CD4⁺ T-cells, HIV, macrophages, Mtb, and CTL T-cells are given by, respectively. This is found when all pathogen popu- lations are zero. It is given by:

(3)

3.2. Reproductive Number, R₀

The basic reproductive number (R₀) measures the number of new secondary infections generated by a single co-infected individual cell in the presence of CTLs mechanisms. It is a dimensionless parameter which can be used to investigate the potency of the immune system. It can be used to control infections and disease progression so that they are kept at low levels. R₀ is here given as the dominant eigenvalue of the next generation matrix of the Jacobian matrix by Watmough’s method [30] . There are several for system (2), which can be denoted as follows:

・ denoting the reproductive ratio given only when there is only viral infection. This can be defined as the average number of viruses produced by one virus in a mostly susceptible population of CD4⁺ T-cells.

・ denoting the reproductive ratio given only when there is Mtb infection. It is defined as the average number macrophages that can be infected from a single Mtb bacteruim in a mostly susceptible population of macrophages.

・ denoting the reproductive ratio when there is co-infection and given as

(4)

Diseases are not competing, therefore an individual can die of either HIV or Mtb or both and so they both contribute to overall rather than considering the maximum value of the next generation matrix.

4. Endemic States Analysis

The model system (2) has three endemic states: the virally infected state (where only the HIV pathogen is present), the Mtb state (which represents the presence of the Mtb pathogen only) and the co-infected state (where both pathogens are present). The stability analysis of these states is here discussed and analysed using the Jacobian method.

4.1. Virally Infected State

The population density of the uninfected CD4⁺ T-cells, infected CD4⁺ T-cells, Virus, Mtb, Macrophages and the HIV specific CTLs at the virally infected endemic state are respectively given by as:

(5)

where. The uninfected CD4⁺ T-cells population density is given by

(6)

is positive when. That is, the cells only exist when the condition is satisfied. The population increases with increase in the inhibition of viral entry, replication rate and direct killings by the CTLs attribute which again shows a protective effect by the CTLs. The population of uninfected CD4⁺ T-cells decreases with increase in the HIV infection rate and increase in viral production (due to replication and bursting) as explained in system (2), which attributes to increase in. Thus increase in reduces population and vice versa.

The abundance of the infected CD4⁺ T-cells at the virally infected state is given by

(7)

This is effectively reduced by increase in the inhibition of viral infection and direct killing of the virus by the CTLs. The population however, increases with increase in the viral population which inturn increases the reproductive ratio.

The viral load at this endemic steady state is given by the expression:

(8)

The equilibrium value of the viral load is dependent on the average number of the new viruses produced by the infected macrophages as well as infected CD4⁺ T-cells. Increase in the viral production attribute to an increase in the viral load. This viral population is however, reduced by the effectiveness of the CTLs to inhibit viral pro- duction and replication, a mechanism of the CTLs that reduces viral multiplication and protects the CD4⁺ T-cells. Thus, inclusion of these mechanisms in the new model helps to understand how the virus can be reduced. Positivity of the viral population is possible when.

The macrophage population is given by

(9)

This population is sustained when and it is reduced with increase in the viral load.

Finally, the HIV specific CTLs population density is given by:

(10)

Increase in the viral population density increases the R_0v which then stimulate more CTL to be released to either directly kill the virus via their phagocytic nature or inhibit replication and more infections although it also depends on the rate of production of

the CTLs from the source. This is possible when the condition is satisfied.

4.2. Mtb Equilibrium State

The second endemic equilibrium state is the Mtb infected steady state where the viral load and the infected T-cell populations are all zeros and is given by:

(11)

where and, , , are the equilibrium values showing the abundance of the uninfected T-cells, macrophages, Mtb population and the HIV specific CTLs, respectively, and the values are given by expressions (12)-(15). The infected T-cell equilibrium value at the Mtb endemic steady state is given by:

(12)

The uninfected CD4⁺ T-cells density exist only if. It depends mainly on the rate at which they are being produced, their natural death and the proliferation rate due to infection by the Mtb. More Mtb infections trigger release of more CD4⁺ T-cells. The protective effect of the CTLs is not exihited at this equilibrium state since they are HIV specific.

The macrophages are given by:

(13)

This value is dependent on the interactions of the macrophages with the Mtb patho- gen and the natural death rate for the macrophages. When Mtb approaches zero then the macrophage population goes to the uninfected steady state value of. The value of the CTLs at this endemic state is the same as the one at the uninfected steady state since the CTLs are not involved in the controlling of Mtb as they are HIV specific. Thus

(14)

The Mtb population at the Mtb endemic steady state is given by the following ex- pression:

(15)

The equilibrium value depends totally on the interaction of the Mtb with the macro- phages and the killing by the CD8⁺ T-cells together with the Mtb natural death rate and the Mtb carrying capacity. Mtb exists only if the following condition is satisfied

(16)

4.3. Co-Infected State

The last endemic state is the co-infected endemic state where both pathogens are present given by

(17)

where, , , , , are the equilibrium values at the co-infected steady state. The abundance of the viral load and the CTL equilibrium values are given by (8) and (14) respectively, same values as the ones at the virally infected steady state except that the uninfected T-cell values are replaced by. The Mtb population again is still the same as the one at the Mtb endemic state, expression (15). The abundance of the uninfected CD4⁺ T-cells at the co-infected steady state is given by

(18)

where are given by equations in Appendix (10.1). This shows that the uninfected CD4⁺ T-cells are reduced more at the co-infected steady state due to the virus and also due to the Mtb infection. The macrophage density at the co-infected steady state is given by

(19)

where for the macrophages to be feasible at the co-infected equilibrium state. Thus, the value of the macrophages are seriously reduced in a co-infected individual due to the presence of both pathogens which reduce the macro- phage population. The uninfected T-cells steady state value for the co-infected endemic state cannot be explicitly found since it involves a polynomial of higher order. However, it can be noted that the abundance of uninfected CD4⁺ T-cells is reduced due to the presence of both pathogens. This is only possible when we have both the and the being greater than unity for the co-infected state to be established.

5. Stability Analysis

5.1. Disease Free State,

Stability analysis of all the steady states are here done using the characteristic poly- nomial of the Jacobian matrix at each equilibrium state for all our equilibrium states. The stability analysis of the uninfected steady is analysed using in Appendix (10.2). The eigenvalues are calculated by solving the characteristic polynomial

where and are given in Appendix (10.2). All the four eigenvalues are negative when

(20)

The other two eigenvalues are obtained from the quadratic equation

which has negative roots if and only if and. This is only possible if

(21)

Stability of requires that the Mtb carrying capacity is satisfied by condition (20). The same condition is required for system (1) that [22] , where are the critical values for the Mtb carrying capacity in system (1) and (2), respectively. This is due to the fact that the CTLs incorporated in system (2) are only HIV specific and therefore does not change mechanisms in the Mtb dynamics. Thus with or without the CTL factors, stability of the disease free equilibrium is achievable when. Condition given by 18 is true when. The second con- dition for stability of is dependent on the number of produced by infected CD4⁺ T-cells,. Stability depends on which is dependent on the CTL’s ability to directly kill the virus, inhibit viral infection and replication over and above the same other factors as system (1). Also of interest is the reduction by the CTL factor to production of more viruses by macrophages. Therefore as either one or a combination of. Condition (21) is only possible when. Thus is stable when both are less than unity. Unlike in system (1), where stability of uninfected state depends solely on the CD4⁺ T-cells production and macro- phages ability to produce more viruses only as shown by [22] , in system (2) stability of happens o when, and is reduced as we increase CTL mechanisms. This limits disease progression, suppose we are to increase these mechanisms since is reduced., new/secondary infections by the virus is reduced. Therefore increasing these CTL mechanisms results in reducing the overal, which also have an impact of protecting the CD4⁺ T-cells since new infections are reduced. If a vaccine can be improvised, it will be helpful to enhance these CTLs factors to reduces viral replication and new infections. loose its stability to either, or through the critical values of and.

5.2. Virally Infected State

Stability of cannot be done explicitly from the eigenvalues of in appendix (10.3) since the steady state values for the viral load are not explicitly found. However, one of the eigenvalues, can be easily read from and is equal to one of the eigen- values from in (10.2) corresponding to condition (20). This implies that for the virally infected state to be stable we need to have same condition established by Kirshner [22] for system (1). When then we have the virally endemic steady state loosing stability to either or. This leads to a state where by the virus establishes itself fast and hence quick progression to AIDS. It is therefore necessary to keep so that the clinical picture of the HIV infection is maintained at low levels by the immune system. Any changes in the Mtb carrying capa- city have a profound effect on the stability of the Stability of. Thus, distur- bances in the Mtb natural death rate and Mtb interaction with both the T-cells and the macrophages then brings qualitative changes to the stability of the virally infected steady state and hence the clinical picture of HIV infected individual in particular. Therefore can also be used to control infection.

5.3. Mtb Infectected State

At Mtb infected state stability is characterised by the characteristic polynomial of given by

where are all given in Appendix (10.4). One of the eigenvalues can be read directly from the Jacobian that is the other two eigenvalues are calculated from the characteristic polynomial of the following deter- minant

The roots are negative if and only if which implies giving the same condition as in requirement condition (21). This condition is true when that is () and when and given by Equation (4). Stability of the Mtb state state arises when the reproductive ratio for the HIV is kept below unity. However, it must also be noted that mainly depends on the effector mechanisms of the CTLs such that any slight changes in these CTL mechanisms significantly changes condition (21) hence the stability of the Mtb infected endemic steady state. The state of the last three eigenvalues can be determined from the following theorem.

Theorem 1 Let with real and which is assumed if then scale the whole expression with −1 which does not change the zeros of. Then have roots with negative real parts if and only if the routh determinants of the polynomial are all positive where

Thus, from the theorem we have the Mtb infected endemic state stable since the other roots of the Jacobian matrix have negative real parts since the routh determinants of the polynomial are all positive where

The Mtb infected steady state can only be stable also when the which is given by the condition

(20)

Therefore, stability of the Mtb infected steady state is stable when and. The same critical points and determine stability for both the Mtb infected and the virally infected endemic states. Thus, there exists a switching behavior on stability between and via these parameters. looses its stability via and to and also to via both and. This implies transcritical bifurcations at these points although they are not analysed in detail in this paper.

5.4. Co-Infected State

The co-infected endemic steady state can only be stable when the number of pathogens for both diseases are greater than zero and this corresponds to the condition when and when. Thus both and are greater than unity, imply- ing that as long as both pathogens exist, an individual always remains in the co-infected state which makes it very difficult to control the disease.

6. Numerical Simulations

Matlab 6.5 version was used for all our simulations for both models using ODE45 solver. Simulations on this model give us a portrait of the general behaviour of immune cells population in the presence of the HIV and Mtb pathogens. We are also concerned about the parameters which are of importance in stabilising the model and the ranges in which the system is stable and unstable. Table 1 shows all the parameter values used for all our simulations are here in used. The initial condition for systems (1) and (2) are given as, , , , and adopted from [22] [27] .

7. Effects of CTL Mechanisms

7.1. Effects of CTLS on R₀

The presence of the lytic factor is almost insignificant in a co-infected state since it depicts the severe stage of HIV and Mtb. The different mechanisms affect the repro- ductive ratio differently. Figure 1(a) shows how changes when there is only inhibition of infection, replication and direct killing by CTLs, given by, , and, respectively. The ratios generally decrease with CTL mechanisms. It shows that the lytic factors are more essential than the non-lytic factors in the order of and. It also shows that although the reproductive ratio is reduced with increase in CTL mechanisms, it will never be reduced to zero. This is because of the nature of HIV which is a retrovirus thus we will always have the virus once a person is infected. A combination of the different mechanisms here not shown was also done numerically and observed that the reproductive ratio is reduced more when all the mechanisms are enhanced [31] . Removing any one of the CTL mechanisms will result in a high ratio which depends on and. Thus condition means the rate of CTL

mediated killings is low relative to the rate of cell-mediated killings and means that the rate of virus induced CD4⁺ T-cells killings is very high relative to the rate of CTL mediated killing [27] . The reproductive ratio here shows that for both high and low values of CTLs (and) and, then the order of the ratios is [31] . An indication that the non-lytic arm of the CTLs is more essential than the lytic arm when for both low and high levels of the CTLs, since the ratios are generally low when non-lytic arm are in operation than when the

lytic arm is in operation. Here the are defined in terms of given by system (23). Hence, chances of controlling infection by the immune system are increased when the non-lytic factors are in operation. If, then the order of the reproductive ratios is given by for both low and high levels of the CTLs. This implies that for this condition, we have the lytic factors being more effective than the non- lytic factors as ratios are lower when the lytic factors are in operation than when only non lytic factors is involved. In general, we also have lower values of the reproductive ratios for higher values of CTLs being lower than for low CTL values indicating the importance of increased involvement of the effector mechanisms of the CTLs. Therefore the CTLs have a very vital role to play in the control of HIV infection in a co-infected individual as it lowers significantly the reproductive ratio hence protect CD4⁺ T cell infection by keeping a low viral load and hence keeping the Mtb carrying capacity lower than.

7.2. Cell Population

There is also evidence of the uninfected CD4⁺ T-cell depletion due the presence of CTL mechanisms as shown by Figure 1(b) and Figure 1(c). The viral population can never reach out to higher levels above in the presence of CTLs as shown in Figure 1(c) but reach up to levels of in the model by Kirshner [22] as in Figure 1(b). Thus the presence of these mechanisms limits the viral population growth and hence limit the depletion of CD4⁺ T-cells. This has an effect of reducing the rate of progression to the AIDS state. The different combinations of the CTL mechanisms can be analysed on the equilibrium values of all the variables. Each of the equilibrium values is then plotted against time for the different combinations. In this paper, only the different combi- nations under viral population is analysed although all the other populations were done but not represented as in Figure 1(d). It must also be noted that the other results agree with those on the viral load. Figure 1(d) shows that a combination of direct killing of the virus and hinderance of viral replication will go a long way in reducing the viral load. represent the following scenarios:

(23)

8. Conclusions

The HIV specific CTLs have a very big role to play in limiting viral spread and con- trolling infection by the virus in the immune system, which means that they have profound effects to the dynamics of the co-infection of Mtb and HIV in general. In the early stages of infection when the HIV specific CTLs are still in small amounts, we have noticed that the lytic factors are more important than the non-lytic factors and reaching the AIDS state is accelerated when the lytic factors are limited in the immune system, a weakness of our basic model by Kirshner [22] since it had no mechanisms of the CTL effects. CTLs are believed to be in abundance at the chronic stage of HIV infection and hence when, the non-lytic factors become more effective than the lytic ones. This implies that both arms of the CTLs are essential for the immune system to control infection. The same conditions were deduced by other authors [27] .

The study shows that both the lytic factors and the non-lytic factors are important in the controlling of HIV infection in a co-infected individual. The non-lytic mechanisms are more effective in controlling infection in both cases when rate of CTL mediated killings is low relative to the rate of cell-mediated killings. The lytic factors are more important when rate of virus induced CD4⁺ T-cells killings is very high relative to the rate of CTL mediated killing regardless of the CTL levels. However, the lytic arm is more important when it comes to control infection than replication since it is believed that CTLs will remain high and non-lytic arms are more important in controlling replication of the virus as they are believed to be more effective at the chronic stage of the infection [27] as also confirmed by Figure 1(a). The CTLs’ ability to hinder viral replication protects the clinical picture of a co-infected individual hence protecting the individual from fast AIDS stage as witnessed by Figure 1(a), Figure 1(b). Effectively the presence of CTLs reduces the viral load levels and protects the CD4⁺ T cell levels. Thus, we can conclude that the effector mechanisms of the HIV specific CTLs are relevant in controlling infection by the immune system although there is need to deter- mine which on-lytic factors are more important at the chronic phase. The increase in the CTLs mechanisms reduces viral multiplication, which results on the reduction of viral load, with the non-lytic factors being more effective in viral load reduction. Reduction of the viral load protects the macrophages too, thereby slowing down the rate of progression to AIDS. Thus, if drugs can be put in place to enhance these CTL mechanisms either as a vaccine or treatment, then rate of depletion of CD4 count is reduced and macrophages are protected. Ultimately, the progression to AIDS state is reduced thereby increasing the life span of individual co-infected by HIV and Mtb.

Acknowledgements

This research was made possible due to the support and insights from Dr G. Magom- bedze. Thank you very much.

Cite this paper

Mufudza, C., Hove-Musekwa, S.D. and Chiyaka, E.T. (2016) Effects of the Cytotoxic T-Cells on the Dynamics of Co-Infection of HIV-1 and Mycobacterium tuberculosis. Journal of Tuberculosis Research, 4, 191-212. http://dx.doi.org/10.4236/jtr.2016.44022

References

Appendix

10.1. A1

10.2. A2

where

The eigenvalues are calculated by solving the characteristic polynomial of the Jacobian matrix which can be expanded to become

where

10.3. A3

The Jacobian matrix evaluated at the virally infected endemic steady state is given by

where

10.4. A4

where

the characteristic polynomial of the is given by

where