Geomaterials
Vol.3 No.3(2013), Article ID:34609,9 pages DOI:10.4236/gm.2013.33014
Generalization of Wave Motions and Application to Porous Media
Wizard Technology, Teramo, Italy
Email: romolo.difrancesco@gmail.com
Copyright © 2013 Romolo Di Francesco. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 22, 2013; revised June 22, 2013; accepted July 1, 2013
Keywords: D’Alambert; Wave Motions; Propagation One/Two/Three-Dimensional; Porous Media
ABSTRACT
The examination of wave motions is traditionally based on the differential equation of D’Alambert, the solution of which describes the motion along a single dimension, while its bidimensional extension takes on the concept of plane waves. Considering these elements and/or limits, the research is divided into two parts: in the first are written the differential equations relating on the conditions two/three-dimensional for which the exact solutions are found; in the second the concepts are extended to the analysis of the propagation of wave motions in porous media both artificial and natural. In the end the work is completed by a series of tests, which show the high reliability of the physical-mathematical models proposed.
1. Introduction
The mathematical theory, that analysed the propagation of elastic impulses, has its origin from the mechanics of the wave motions the latter are defined as the integral of a force generated naturally (example: earthquake) or artificially (example: geophysical prospecting; vehicular traffic), time-averaged:
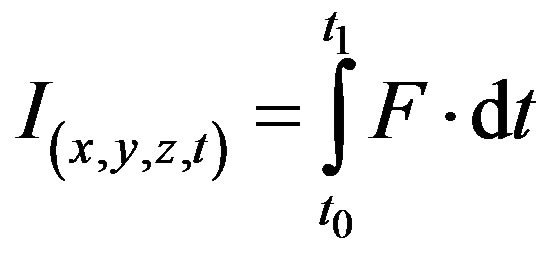 . (1)
. (1)
Also, the wave nature assumed for the analysis of the phenomenon implies the propagations time of the impulse in accordance with the relationships between the dynamic elastic modules—longitudinal (Ed), tangential (Gd) and volumetric (Kd)—through the dynamic Poisson’s ratio (νd) in turn dependent on the speed of compressions waves (vS):
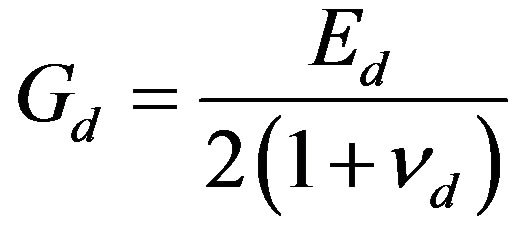 (2a)
(2a)
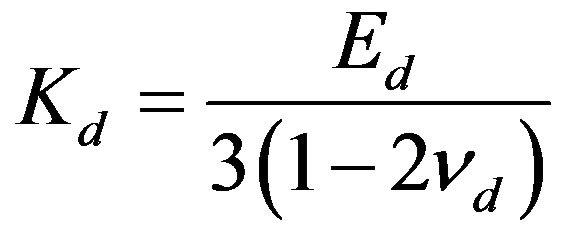 (2b)
(2b)
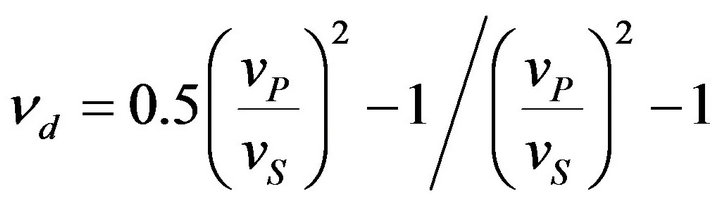 . (2c)
. (2c)
Known these elements (Figure 1(a)), the analysis of

Figure 1. (a) The dynamic modules belong to the initial phase of the stress-strain curves, relevant to the field of small deformations, the limit of which is set at ε = 1% [1,2]: identification of motion parameters of two identical periodic waves, but out of phase between their (Δδ = π/2).
the vibratory phenomenon is attributable to the study of elastic behaviour of the individual waves, that exploit the properties of sine and cosine functions and are repeated periodically in the initial characteristics of the motion, expressed in terms of amplitude A, frequency f and phase costant δ (Figure 1(b)); other fundamental parameters of the motion are: the period:
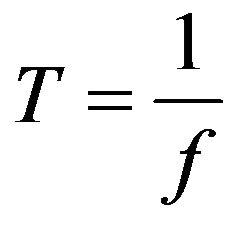 , (3)
, (3)
the angular pulsation (or angular frequency):
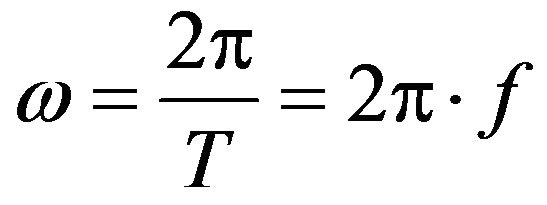 , (4)
, (4)
And the number of the wave:
 . (5)
. (5)
In turn the Equations (4) and (5) can be combined to derive the expression of velocity:
 . (6)
. (6)
Given that the real motions (example: earthquake) can be simulated by the addition of a suitable number of monochromatic waves (Figure 1(b)) each characterized by its own amplitude, frequency and phase (Figure 2).
Under these conditions, a mathematical model of general validity and its extension to the porous media will be described in the continuation of research.
1.1. The 1-D Equation of D’Alambert
The analysis of vibratory motions originates from the
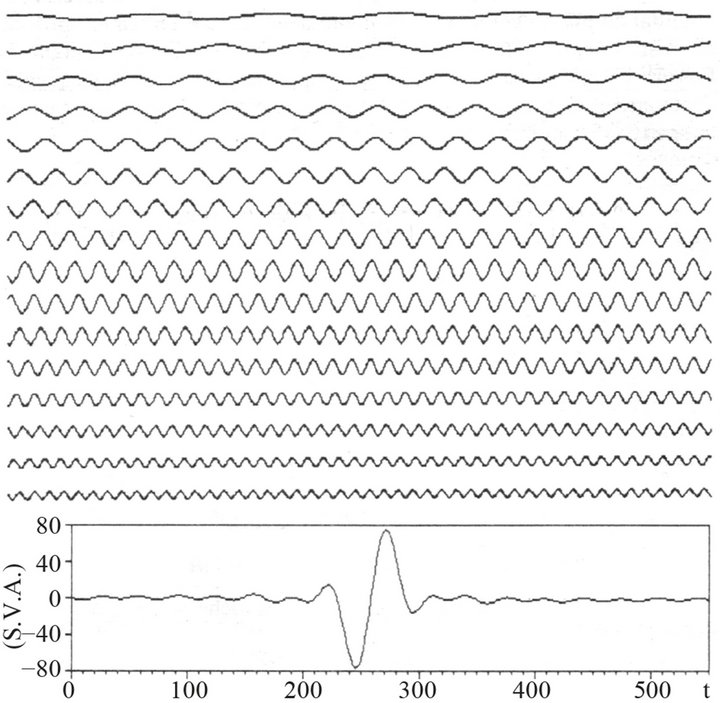
Figure 2. Schematic reproduction of an artificial impulse and of the sixteen monochromatics components [3].
D’Alembert’s differential equation [4,5] which analyze the propagation of monodimensional waves in function of the vectorial component u of the movement (variable between A = 0 and A = 1—Figure 1(b)) in a media with speed vx:
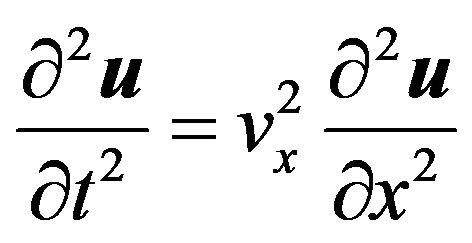 . (7)
. (7)
The solution of this problem, provided by the author, has been perfected by Euler [6] in the following form expressed in relation to of the elements described by the Equations (3)-(5):
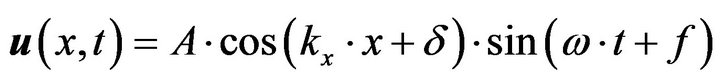 . (8)
. (8)
In fact, calculated the second derivatives of the Equation (8) as a function of space and time:
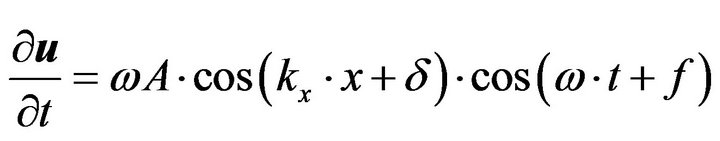 , (9a)
, (9a)
 , (9b)
, (9b)
 , (9c)
, (9c)
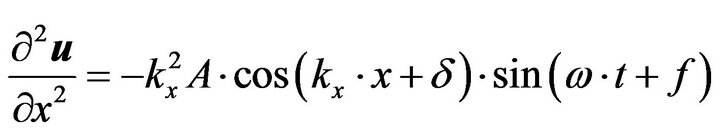 , (9d)
, (9d)
you can replace the Equations (9b), (9d) and (6) in the Equation (7) to obtain the identity:
 . (10)
. (10)
Alternatively, can be introduced only Equations (9b) and (9d) to obtain the Equation (7).
1.2. The Plane Waves
The extension of D’Alembert equation to the two-dimensional case is an unsolved problem that has required the introduction of isotropic homogeneous media in which the motions are propagated as circular waves (Figure 3); at considerable distances from the source, small portions of the circular waves can be approximated by plane waves which propagate in a straight line according to directions normal to the wave fronts represented by the rays; in this way the analysis of the phenomenon is facilitated, as limited to the study of the suns rays having evidently rectilinear trajectories in homogeneous media and curvilinear in those non-homogeneous.
1.3. The Phenomenon of Dispersion
Each monochromatic components of a vibratory motion which propagates in a homogeneous medium travels at the same speed, in turn, dependent on the angular fre-
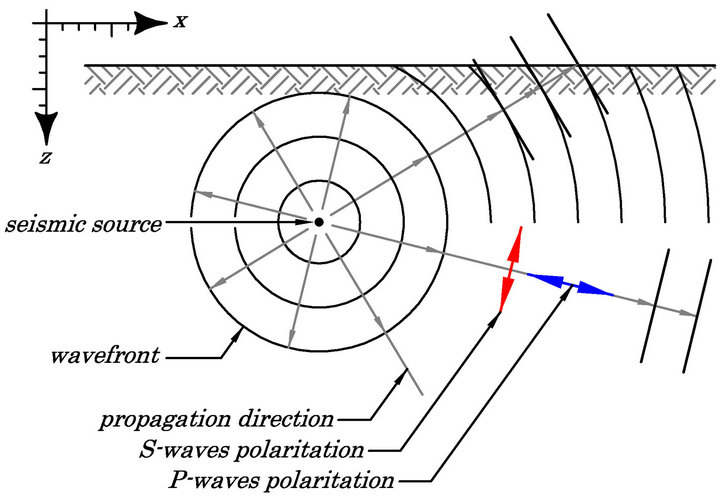
Figure 3. In homogeneous isotropic media the P and S waves propagate according to concentric spheres (circles in the plane) at a great distance can be approximated by the wave fronts plans generically definited plane wave.
quency and the wave number through Equation (6); in this case, indicated with ρ the density of the medium, it proves [7] that the following equations are valid, for elastic waves compressional (P) and cutting (S):
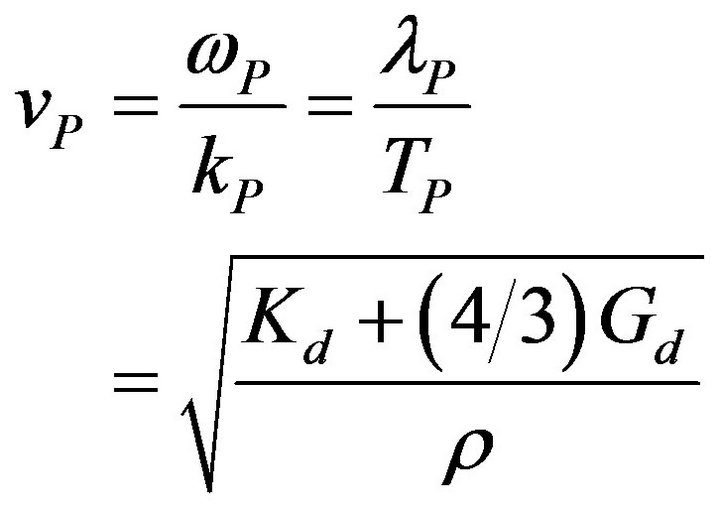 , (11a)
, (11a)
 . (11b)
. (11b)
Besides, it is also the relationship vP > vS for the Equation (2a). In inhomogeneous media, for which the speed varies along the path, each frequency component of the vibratory motion is instead equipped with its own speed, such as to arrive to a generic receiver at different times. The described phenomenon, known as the dispersion of the phases, implies that in the means of non-dispersive (homogeneous) the vibratory motion arrives at the receivers with the same initial shape; on the contrary, in dispersive media is possible to identify a group velocity (if you choose to characterize the group through the analysis of the maximum amplitude) and a phase velocity of each component, so that a signal emitted by the source arrives distorted at the receiver. Obviously, means in the two non-dispersive group velocity and phase are.
2. General Equation of the Wave Motion
Denote by s(x,y,z) the displacement vector in space, defined with respect to a reference system coordinated, having components u, v e w; consequently, if the Equation (7) describes the motion of a disturbance which is propagated only in the direction x, the generalized form of the equation of motion will be of the type:
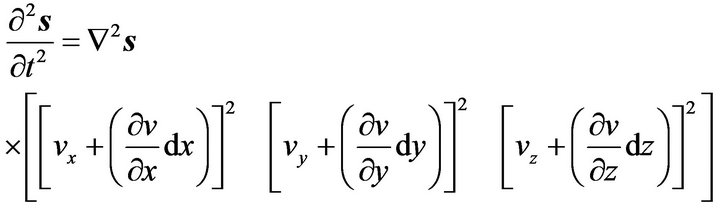
(12a)
 . (12b)
. (12b)
2.1. The Equation of Wave Motion in Space
The Equation (12), expressed in matrix and extended form, in the case of the means non-dispersive, reduces to the form:
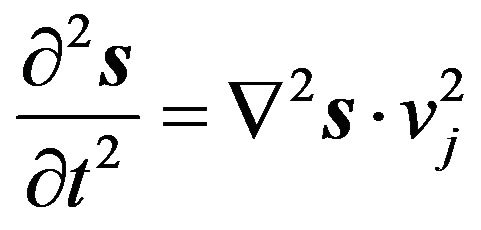 , (13a)
, (13a)
 , (13b)
, (13b)
in which vj identifies the column vector of the speed.
Then, the solution can still be expressed using the Equation (8) on condition to take account of the threedimensionality of the phenomenon:
 . (14)
. (14)
By repeating the procedure previously seen with Equation (7) of the motion 1D, you get in sequence:
 , (15a)
, (15a)
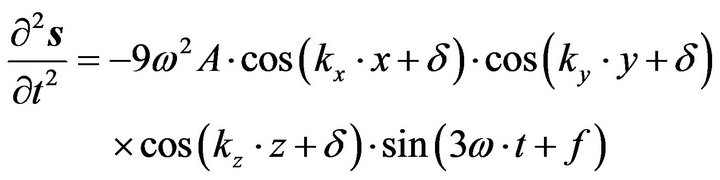 , (15b)
, (15b)
 , (15c)
, (15c)
 , (15d)
, (15d)
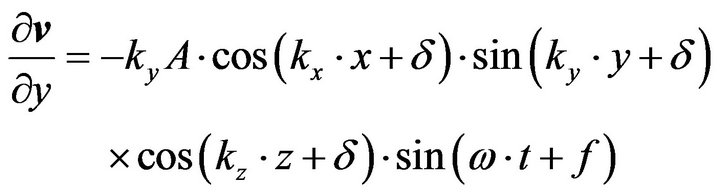 , (15e)
, (15e)
 , (15f)
, (15f)
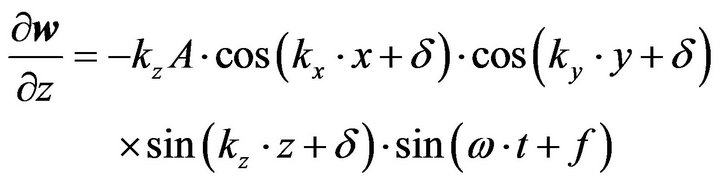 , (15g)
, (15g)
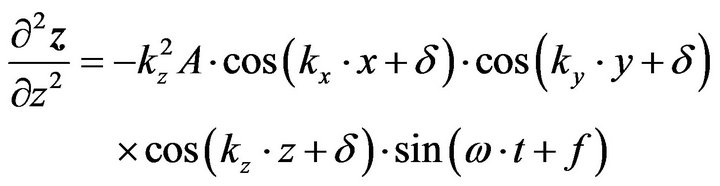 , (15h)
, (15h)
 . (16)
. (16)
In Equation (16), replace the components of the velocity, expressed according to Equation (6), finally to prove the validity of the proposed solution:
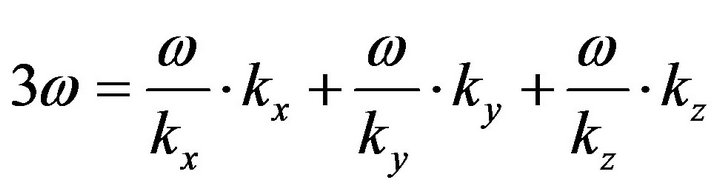 . (17)
. (17)
The latter also demonstrates that the fundamental period of the wave (and consequently the frequency fundamental) corresponds to the period (and frequency) of the individual components.
In conclusion, for orthotropic media and from the structure of Equation (14), which is easily seen that the waves propagate according ellipsoids scalene (Figure 4(a)); similarly, for the condition vz > vy = vx we are seeing waves with the form of ellipsoids of revolution (Figure 4(b)) while the condition vz = vy = vx leads to the development of spherical waves (Figure 4(c)). In this regard, we can rewrite Equation (16) creating the conditions:
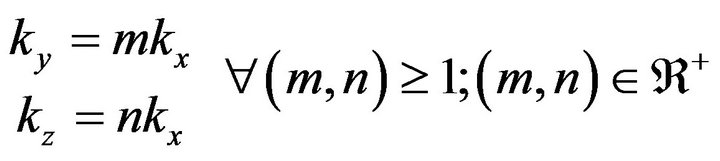 , (18)
, (18)
obtaining:
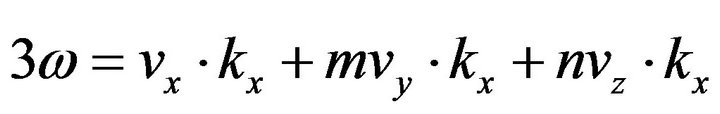 , (19a)
, (19a)
 . (19b)
. (19b)
Place also:

Figure 4. Three-dimentional geometry of waves: (a) Scalene ellipsoid (vz > vy > vx); (b) Ellipsoid of revolution (vz > vy = vx); (c) Sphere (vz = vy = vx).
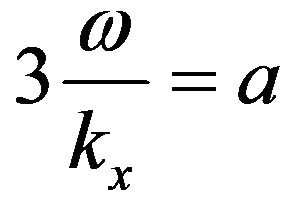 , (20)
, (20)
you get:
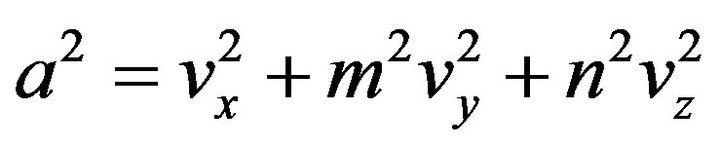 , (21a)
, (21a)
 . (21b)
. (21b)
Finally, putting too:
 , (23)
, (23)
we come to the equation of an ellipsoid:
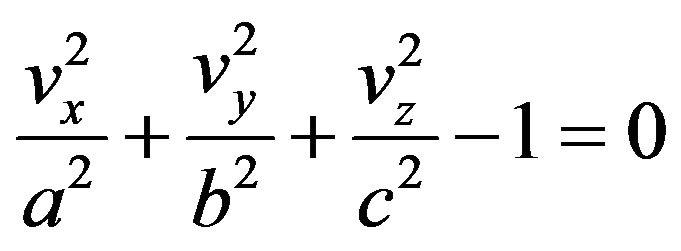 . (24)
. (24)
On the other hand, the Laplacian content in Equation general (13a)—Ñ2s—is the quadratic form of the divergence of the vector functions that, for positives values in a generic point P denotes the existence of an outgoing flow in the neighborhood of P; so, to the condition imposed vz > vy > vx corresponds w > v > u which describes an ellipsoid. The discussed model is independent of temperature of the system assumed adiabatic, that respects the law of conservation of energy.
2.2. The Equation of Wave Motion on a Plane
In case of the plane x z the Equation (13b) is reduced on the form:
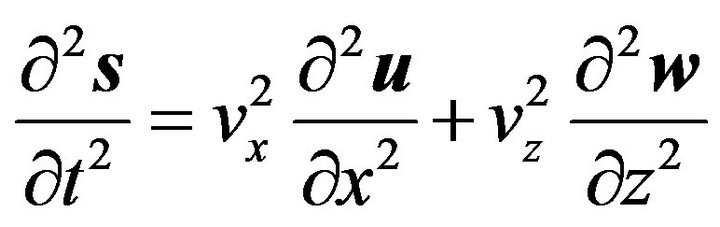 , (25)
, (25)
whose solution is a special case of the Equation (14):
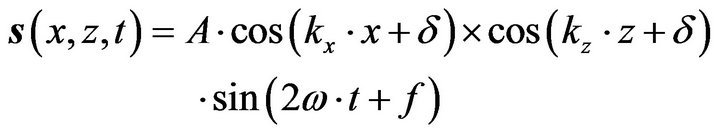 . (26)
. (26)
Again, the procedure is applied now known we arrive at the identity relation:
 , (27)
, (27)
which proves the accuracy of the solution according to the propagation of the waves on a plane with elliptical or circular forms.
3. The Propagation of Waves in Porous Media
The problem of waves propagation in porous media has been addressed previously in [8] from the law of mass balance for two-phase media now extended to threephase drives:
 . (28)
. (28)
In the Equation (28) appear porosity (n), the degree of saturation (S) and the density of the solid phase (ρs), fluida (ρw) and gaseous (ρa) capable of describing a structure consisting of a skeleton solid with interstitial interconnected pores between them (Figure 5).
Since the mass is connected with the speed, through the Equations (11), (2a) and (2b) shows a dependence of the type:
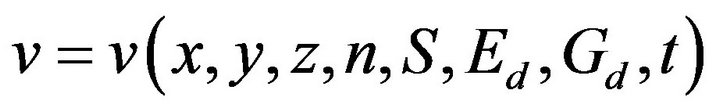 . (29)
. (29)
In other words, must be considered as a porous solid consists of three continuous elastic means that occupy the same region of space and which interact between them carving up the propagation of the same elastic pulse.
3.1. Speed of Compression Waves in Porous Media
The problem outlined can be mathematically simplified if one analyzes the propagation of three waves decoupled from the same impulse, through the solid skeleton and phases fluid and gases contained in the pores (Figure 6); in this way we obtain a system of three equations for the propagation of compression waves in anisotropic porous media:
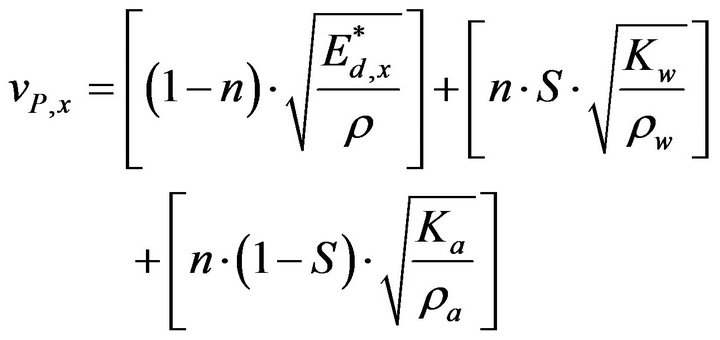 (30a)
(30a)
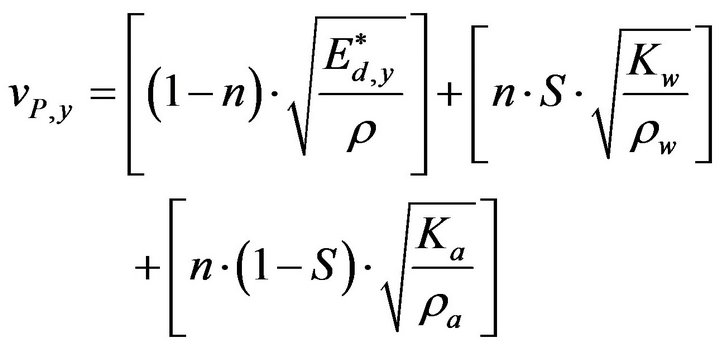 , (30b)
, (30b)
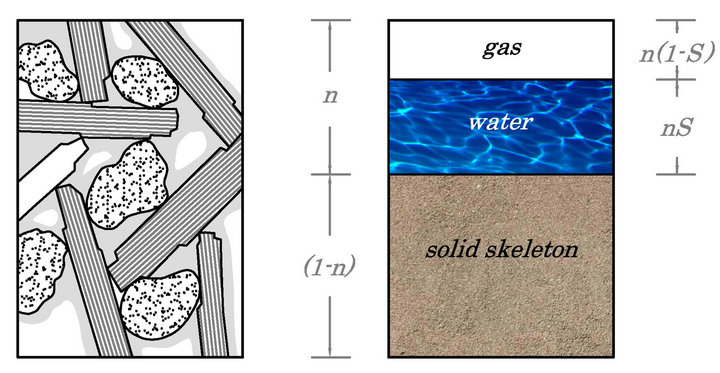
Figure 5. Typical structure of soils and identification of the basic parameters of porous media in general [9].

Figure 6. The basic hypothesis involves the schematization of porous media in three continuous elastic means and in this way an impulse can be decoupled into three components which propagate without mutual interaction.
 . (30c)
. (30c)
Analyzing the Equation (30) analyzing the equation it turns out that the first bracket identifies the anisotropic component, relative to the propagation through the solid skeleton, linked with only the elastic modulus being able to neglect the effect of the transverse contraction [10] for having brought the problem to three one-dimensional waves; the following brackets indicate instead the components related to the isotropic liquid and vapor phases through the corresponding elastic moduli volumetric (Kw e Ka).
The symbol E*d,i identifies a law of variation of the longitudinal elastic modulus dynamic, determined from [11] and [12] and based on the introduction of factors of contraction seen in [13]:
 . (31)
. (31)
In the Equation (31) appear the parameterawhich represents a material constant and must be determinated experimentally, meanwhile the value of ρ, presents in the Equations (30) changes as a function of the porosity according to the law (28) of the mass balance.
Once defined the general structure of the equations, the problem can be further simplified if one considers that the speed of propagation of the impulses in water and air are approximately vw ≈ 1500 m/s and va ≈ 340 m/s which would alter the Equations (30):
 , (32a)
, (32a)
 , (32b)
, (32b)
 . (32c)
. (32c)
In conclusion, the same way as seen with the Equations (13) ÷ (19) related to the generalized theory of waves, the Equations (30) and (32) describe scalene ellipsoidal waves, ellipsoid of revolution or spherical with respect to the relationships between the elastic modulus of the soil skeleton that affect the dynamic response of the anisotropic component.
3.2. Velocity of the Shear Wave on Porous Media
In the determination of the speed of shear waves is necessary to consider: 1) the physical impossibility of waves to propagate in fluids; 2) their polarization on mutually orthogonal planes (waves SV e SH); 3) their development in all directions with respect to the source; 4) to Equation (11b); 5) a law of variation of Poisson’s ratio:
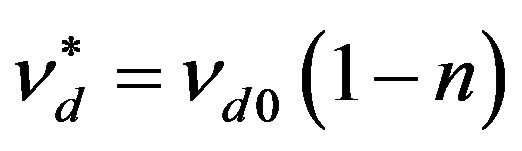 . (33)
. (33)
Finally, the Equations (2a), (31) and (34) can be combined with each other:
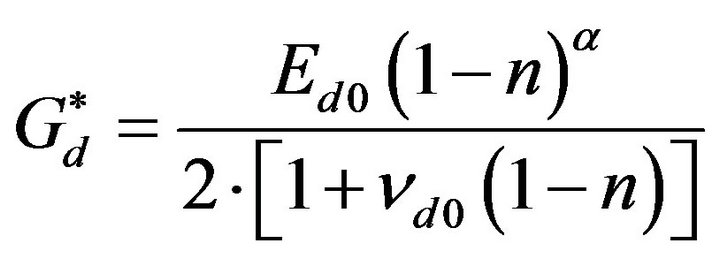 . (34)
. (34)
Using the Figure 7 as a reference it is seen that the components of the shear waves are 6, of which three independent mathematical symmetry and, accordingly, the related formulations can be obtained from Equations (32) purified from the isotropic components:
 , (35a)
, (35a)
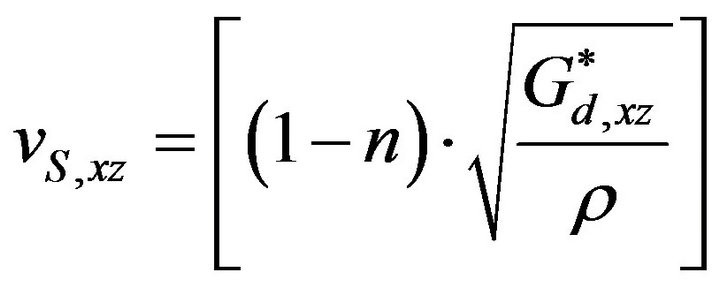 , (35b)
, (35b)
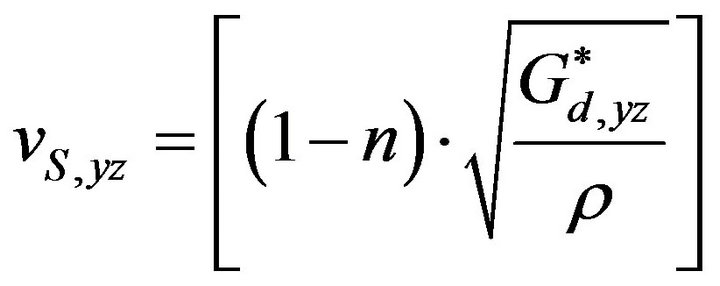 . (35c)
. (35c)
Equations (35), compared with the Equations (32), demonstrate the existence of time differences of arrival of the shear wave—compared to compression—which must necessarily increase with the increase of the distance from the source.
3.3. Tests of Model Validation
The graph of Figure 8 illustrates the experimental results, conducted on both dry rocks that saturated water, expressed in terms of rate of change of P-waves as a

Figure 7. Components of the seismic moment tensor [14].
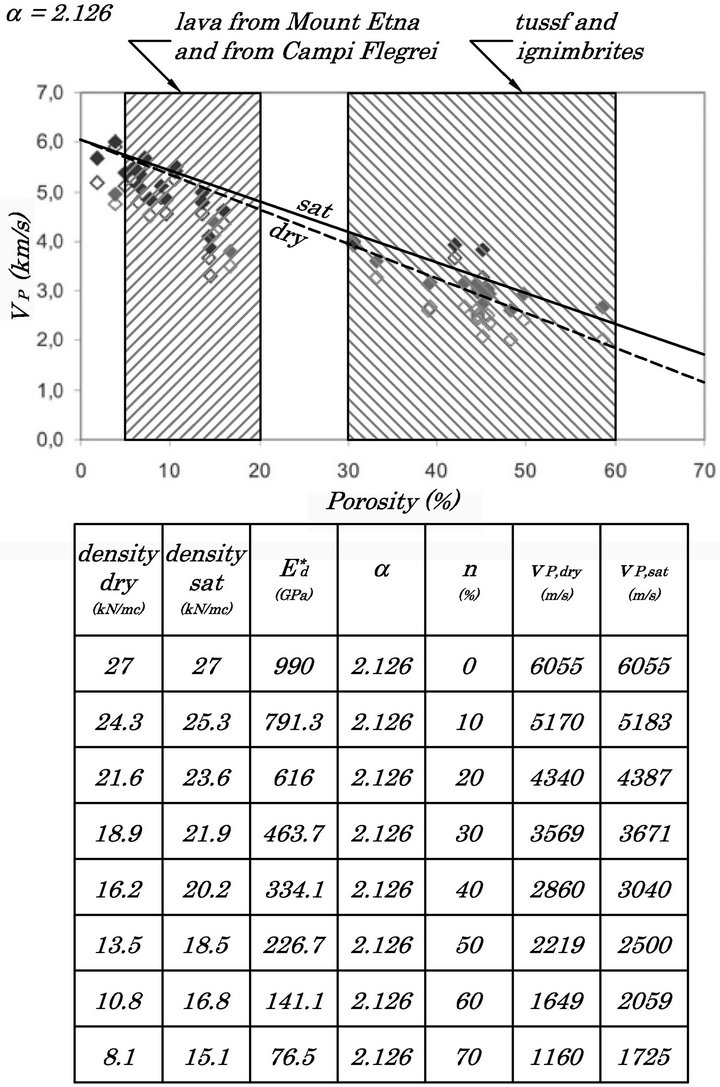
Figure 8. Comparison between the experimental data of the speed of samples of dry rocks and waterlogged [15] and the theoretical results predicted by the model.
function of porosity. In detail, as reported in [15], it is possible to note that the increase due to saturation is very evident both in the lava issued from Etna (ET; near Catania, Italy) than in the Campi Flegrei (CF, Italy near Naples) both characterized by a low overall porosity of approximately in the range n = 5% - 20%, on the contrary, in tuffs and ignimbrites (having a porosity in the range n = 30% - 60%), the increase of speed found in the saturated state is significantly higher than the lava rocks.
At the same graph have been superimposed the theoretical laws of variation of P-waves velocity, and their tabulated data, calculated using Equations (28), (31) and (32c); as can be noted from the same theoretical model fails to approximate, for a = 2.126 introduced in the calculation of , the speed difference between the dry and saturated rocks with the increase of the porosity.
, the speed difference between the dry and saturated rocks with the increase of the porosity.
Final interpretation of the results with the theoretical model must be considered that the theoretical behavior of lava rocks (lavas of Etna and Campi Flegrei) and pyroclastics (tuffs and ignimbrites) was standardized in terms of ρ and of , although the different mineralogical composition (Basalts and Trachytes alkaline in the first case, the variable in the second case [16]) induces to assume the existence of different starting values of the dynamic elastic modulus and density; in other words, the same experimental results are not comparable to each other if not qualitatively, as indeed demonstrated by the dispersion of its employee data from the variation of the physical properties quoted.
, although the different mineralogical composition (Basalts and Trachytes alkaline in the first case, the variable in the second case [16]) induces to assume the existence of different starting values of the dynamic elastic modulus and density; in other words, the same experimental results are not comparable to each other if not qualitatively, as indeed demonstrated by the dispersion of its employee data from the variation of the physical properties quoted.
The second test was performed using the experimental data contained in [17], relating to the correlations vP-n and vS-n measured in samples of alumina ceramic (Al2O3) known for the acid resistance and low thermal conductivity so as to be used as a catalyst in the chemical industry and as a graft material in the biomedical; therefore, with reference to Figure 9(a), it turns out that the theoretical model describes with high accuracy the performance of the P-waves in the ceramic (per a = 1.46) while S waves are sufficiently approximated by n < 15% and approximated for n > 15%.
The Figure 9(b), in turn, illustrates the extension of the theoretical model to the entire range of variability of porosity, between a material infinitely compact (n = 0%) and infinitely porous (n = 100%), expressed in terms of P-waves velocity for dry samples and saturated and Swaves velocity. In this case the elements are key findings
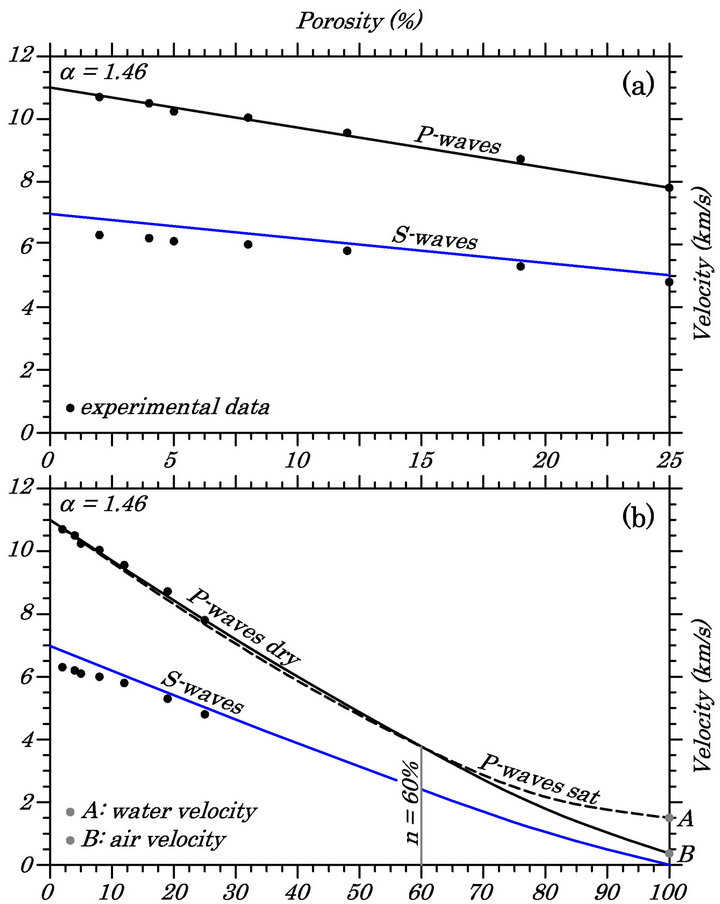
Figure 9. (a) Comparison between the experimental data of the speed of samples of alumina ceramics [17] and the theoretical results predicted by the model; (b) Extension of the model to the entire field of porosity.
in the test: 1) the P-waves velocity for saturated samples is slightly lower than that responsible for the dry samples n < 60%; 2) for n > 60% the P-waves velocity of saturated samples becomes greater than that of the dry samples while the model manifests a marked non-linearity; 3) for n = 100% the speed of the saturated samples is reduced to that of water (point A) while that of the samples dried in the air (point B). Finally, as expected, n = 100% for the S-waves velocity vanishes.
The trends of the P-waves velocity associated to the fields 0 < n < 0.6 and 0.6 < n < 1depend on the laws of variation adopted for ρ and E*d that, described by Equations (28) and (31), respectively are linear and non-linear; which means that, while the density varies linearly for 0 < n < 1 the elastic modulus assumes a-heating an approximately linear for n < 0.6 and not linear for n > 0.6. Consequently, the increase of speed setting attributable to fluid phases fails to compensate—for n < 0.6— the effects adducts by variations in density and elastic modulus.
The last test was conducted using the experimental results contained in [18] and related to the propagation of P-waves in a generic group of rocks not necessarily related to each other (Figure 10); Also in this case, the theoretical model is able to approximate (per a = 2.381) the dynamic behavior generally using the same starting values of the density and the dynamic elastic modulus.
4. Conclusions
The analysis of wave motions takes origin by the differential equation of D’Alembert [4,5], the solution of which, based on the properties of the trigonometric sine and cosine functions, simulates the propagation of an elastic wave in a continuous medium 1-dimensional, and its extension to the floor is brought back to the simplified concept of circular waves reduced to plane waves.
After a brief review of the main elements that make up the rolling waves of D’Alembert, was written the differential equation governing the wave motion in space (generalized theory) to follow, it was found that the exact solution shows that the waves take the form of ellipsoids scalene in orthotropic means which, in turn, reduce to the ellipsoids of revolution in the means transversely isotropic and spherical waves in isotropic media; in the same way, which step consequent, the 3D equation has been reduced to the 2D field whose solution leads to waves having elliptical shapes that are reduced to circular waves. But be aware that these equations are valid for continuous media, which can be described by assigning them appropriate scalar and vector fields defined by means of functions regular and continuous over the entire domain configuration.
Which next step, given the nature of the particle actually real media (with particular reference to geomaterial), the equations have been applied to porous media, the description of which is based on concepts known in Geotechnical that predict the existence of three continuous media (solid skeleton with interparticle voids paths from water and air) that interact between them carving up the propagation of the same impulse elastic divided into the components of compression and shear. Finally, the search has been completed with some tests based on known experimental data relating to the propagation of waves in different types of rocks and in samples of alumina ceramics.
Ultimately, the tests showed that the proposed models fail to accurately simulate the behavior of a particular material or group of materials that share the same origin while further applications may be later developed: 1) in

Figure 10. Comparison between the experimental velocity of P-waves of a generic group of rocks [18] and the theoretical prediction of the proposed model is extended to the field of porosity.
the field seismological, considered that the Equations (30) reduce to Equations (11a) for means infinitely porous, as in the case in which the seismic compressional waves are reduced to acoustic waves when intercept the earth’s surface and propagate into the atmosphere; 2) still in the field seismological or in the analysis of vibrational motions artificial, through the introduction of damping function of the signal; 3) for the determination of the porosity of geomaterials coarse loose that can not be sampled and measured in the laboratory.
5. Acknowledgements
The author wishes to thank Luca Lussari, Department of Mathematics and Physics of “University of Sacro Cuore of Brescia”—Italy, for his suggestions and observations.
REFERENCES
- G. Lanzo and F. Silvestri, “Sismic Local Responce,” Hevelius Edizioni, Benevento, 1999.
- D. Lo Presti, “Behaviour of Soils in Dynamic and Ciclic Conditions,” International Center for Mechanical Sciences—CISM, Udine, Italy, 1999.
- E. Carrara, A. Rapolla and N. Roberti, “Geophysical Survey for the Study of the Subsoil: Geoelectric and Seismic Methods,” Liguori Editore, Napoli, 1992.
- J. D’Alembert, “Research on the Curve Formed by a Rope Set in Vibration,” History of the Royal Academy of Sciences and Belles Letters in Berlin, Vol. 3, 1747, pp. 214-219.
- J. D’Alambert, “Addition to the Memory on the Curve Formed by a Rope Set in Vibration,” History of the Royal Academy of Sciences and Belles Letters in Berlin, Vol. 6, 1750, pp. 355-360.
- C. B. Boyer, “A History of Mathematics,” John Wiley & Sons, New York, 1968.
- L. Landau and E. Lifsits, “Theory of Elasticity,” Editori Riuniti, Roma, 1979.
- R. Di Francesco and M. Siena, “The Contribution of Geophysics in Geotechnical Design and Control Work in Progress,” XXIII National Conference of Geotechnical Engineering, Padova, 16-18 May 2007, pp. 211-218.
- R. Di Francesco, “Introduction to Soil’s Mechanics—Part I,” Dario Flaccovio Editore, Palermo, 2013.
- O. Belluzzi, “Science of Construction—Vol. IV,” Zanichelli Editori, Bologna, 1963.
- G. Ondracek, “The Quantitative Microstructure Field Property Correlation of Multiphase and Porous Materials,” Review on Powder Metallurgy and Physical Ceramics, Vol. 3, No. 3-4, 1987, pp. 205-232.
- D. N. Boccaccini and A. R. Boccaccini, “Dependence of Ultrasonic Velocity on Porosity and Pore Shape in Seintered Materials,” Journal of Nondestructive Evaluation, Vol. 16, No. 4, 1997, pp. 187-192.
- R. Di Francesco, “Introduction to Continum’s Mechanics,” Dario Flaccovio Editore, Palermo, 2012.
- K. Aky and P. G. Richards, “Quantitative Seismology: Theory and Methods,” University Science Books, Sausalito, 2002.
- A. Zollo and A. Emolo, “Earthquakes and Waves. Methods and Practice of Modern Seismology,” Liguori Editori, Napoli, 2011.
- G. Negretti and B. Di Sabatino, “Course of Petrography,” CISU, Rome, 1983.
- M. Asmani, C. Kermel, A. Leriche and M. Ourak, “Influence of Porosity on Young’s Module and Poisson’s Ratio in Alumina Ceramics,” Journal of the European Ceramic Society, 2001, Vol. 21, No. 8, pp. 1081-1086.
- V. Rzhevsky and G. Novik, “The Physics of Rocks,” Mir Publichers, Moscow, 1971.

