American Journal of Computational Mathematics
Vol.06 No.04(2016), Article ID:73149,8 pages
10.4236/ajcm.2016.64035
Improved Video Moving Target Tracking Based on Camshift
Liang Li, Yi Luo
The College of Automation and Electronic Information, Sichuan University of Science & Engineering, Zigong, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 29, 2016; Accepted: December 26, 2016; Published: December 29, 2016
ABSTRACT
Focusing on the failure under the condition of target blocking, the similarity between target color and background color for the Camshift algorithm, an improved algorithm based on Camshift algorithm is proposed. Gaussian mixture model is used to determine the tracking area fast and accurately because it is not sensitive to the external conditions such as light and shadow. Kalman predictor is used to predict the blocked target effectively. The video is processed in the MATLAB environment. The moving target can be tracked and its position can be predicted accurately with the proposed improved algorithm. The results verify the feasibility and effectiveness of the algorithm.
Keywords:
Camshift, Target Tracking, Gaussian Mixture Model, Kalman Prediction, Object Shelter

1. Introduction
Intelligent video processing technology is used in not only the target detection and identification but also tracking, behavior analysis and other aspects of the daily life. The target motion tracking technology has been widely applied in industrial production, traffic management, military and so on. Bradski proposed the improvement [1] of the continuous mean shift and then applied it to the target tracking. What’s more, Camshift is improved in amount situations when the tracking target is heavily sheltered [2] or similar to the environment background in the same hue. Due to the requirement of the initialization manually for Camshift tracking, Wu D [3] proposed the use of inter- frame difference algorithm with low computational complexity and motion prediction based on the previous moment to achieve the effective target tracking in the occlusion. The algorithm can detect the uniform moving object with occlusion, but it failed to take the changes of the actual background environment and state of the tracking object into considerations. Xiu C [4] proposed the use of the weighted saliency to suppress the similarity interference from the background, and identified the target by the reverse probability projection, but did not take target occluded into account. Many scholars take Kalman prediction [5] [6] to estimate the target position which improves the accuracy of the tracking results. Xia J [7] proposed the combination of two-frame-diffe- rence and Camshift to track the target. But with the change of the background and illumination, the foreground is hard to recognize and so is the occluded target. Tang Q [8] proposed the difference method to obtain the target without considering the similarities among the elements easily confused.
Focusing on the issues above, an improved algorithm has been proposed to deal with the background and occluded target. Because of the robustness of illumination and small shiver, Gaussian Mixture Model (GMM) can detect the moving target precisely. Although frame difference can detect the changes between the frames, the small vibration will be the most difficult issue. GMM considers the statistical probabilities of the background rather than the color, frame difference and other details of the textures. Kalman prediction can calculate the position of the moving target whether it is occluded or not.
2. Camshift Algorithm
Since the target histogram is easily affected by the change of the color and illumination, Camshift (Continuously Adaptive Meanshift) algorithm is based on the HSV color space to represent the object. After calculating the component Hue probability distribution and then locating the centroid of the tracking target, the center of the tracking window will adjust to the range of the tracking target by several iterations. Thus we keep track of the target [9] [10] .
The implementation steps of the Camshift algorithm are as follow:
1) The component Hue in the HSV color space is extracted from the current video frames. This will further be used to generate the probability histogram by the color histogram in order to set the tracking window.
2) According to the probability distribution, the zero and first order moments of the image in the tracking window are calculated:
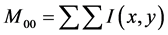 (1)
(1)
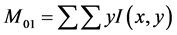 (2)
(2)
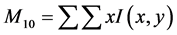 (3)
(3)
And then take the Equation (1), (2) and (3) into Equation (4) separately.
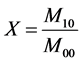 ,
,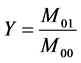 (4)
(4)
3) The fixed tracking window in the Meanshift algorithm has been improved in the Camshift algorithm. The tracking window size is reset according to the pixel probability distribution in the current window, and then the center position of the tracking windows adjusts to the current centroid. This iteration will be stopped until the difference between center and centroid is less than a certain threshold.
4) The step 2 and step 3 are repeated until the difference is less than the set threshold or the iterations times exceed the threshold.
3. Update of the Camshift Algorithm
3.1. Foreground Extraction Based on GMM
As component H in the HSV color space contains the image information, the background change has an effect on the tracking window. GMM which is robust to illumination, small vibration and so on can be used to extract the foreground information. What’s more, GMM can reduce the tracking failure caused by the similarity to the background color.
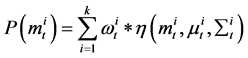 (5)
(5)
 (6)
(6)
where 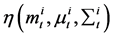 is gauss distribution density function.
is gauss distribution density function. 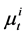 is the mean and
is the mean and 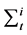 is the covariance of the tth component.
is the covariance of the tth component.
Every object merged in the scene will be decided whether belongs to the foreground or not. The time the process spends will take a long time depending on the number of the Gaussian distribution and learning rate. To alleviate the problem, the idea is to set different number of Gaussian distribution for different region. The region getting close is described by 3 Gaussian distribution while the region far away is described by 1 Gaussian distribution. The learning rate is the strength of the adjustment in the dynamic changes. Considering the estimation accuracy, the original model parameters are improved to adapt to the change better [11] [12] .
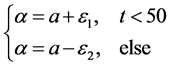 (7)
(7)
Here, 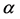 is the learning rate.
is the learning rate.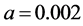 ,
, 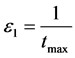 ,
, 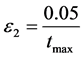
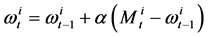 (8)
(8)
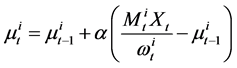 (9)
(9)
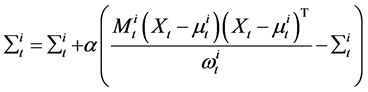 (10)
(10)
3.2. Kalman Prediction
The moving target can be described by the current position and velocity in the time domain [13] [14] . Kalman prediction can accurately predict the coming state of motion and position information, even the target is occluded, and avoids the similar color shift after the median filter algorithm.
The sample time is discrete actually in the target tracking system. It is assumed that the tracking target makes uniform linear motion in a relatively short time, and linear analysis is applied to its motion in discrete time. The Kalman prediction can be expressed as follow:


where the Equation (11) is the state prediction which predicts the current state according to last moment information. A(k) is the state transition matrix, B(k) is the control matrix, and U(k) is the control element. The Equation (12) is state observation process to get the current best estimation.




where P1(k) is the covariance in the prediction process. P(k) is the covariance in the observation process. Q is the model prediction noise. Z(k) is the observation value. H is the observation matrix. V is the model observation noise. R is the covariance of V. D(k) is the Kalman coefficient which is used to adjust the confidence between prediction and observation. The specific steps of our proposed algorithm are shown in Figure 1.
4. Experiment
We evaluate our approach on the 640 × 480 pixels video. The yellow rectangular indicates the motion target by our approach and the green one shows by Camshift algorithm. The experimental hardware platform processor is Pentium Dual-Core 2.5 GHz, 2 GB memory.
Improved GMM is used to extract foreground information more quickly and precisely, and thus locate the tracking target in the scene rapidly. Besides, it avoids the effects of the similarity color between the target and background. From the figures above, the tracking target has the similar color to the shelter. With The improved GMM, it is the book extracted from the foreground rather than the illumination or other textures. Then, the centroid, moving direction and velocity is calculating by Camshift. In Figure 2, the original Camshift tracking detect the object, but it had some area undetected. Our proposed algorithm can detect the whole object by foreground extraction algorithm by improved GMM. After the detecting the tracking target, original Camshift algorithm lost the tracking of the target because of the shelter in Figure 4. Ours can still predict the target’s position by Kalman prediction. Finally, both original Camshift algorithm and ours can detect the tracking target in Figure 6. Nevertheless, ours has more stable and accurate tracking performance than original Camshift algorithm even without the occlusion.
Figure 2 depicts the current position, centroid, moving direction and velocity. Figures 3-6 depict our approach complete the prediction and tracking of the motion target regardless of the occlusion or not.
Figure 1. The flow diagram of our proposed algorithm.
Figure 2. The 85th frame tracking result.
Figure 3. The 110th frame tracking result.
Figure 4. The 123th frame tracking result.
Figure 5. The 157th frame tracking result.
Figure 6. The 185th frame tracking result.
5. Outlook and Conclusion
We have presented an efficient improved algorithm based on the Camshift. The basic idea is to use two cascade algorithms locating the target as well as speeding up the extraction. Future work will focus on reducing the number of the necessary parameters, and improving the real-time performance.
Cite this paper
Li, L. and Luo, Y. (2016) Improved Video Moving Target Tracking Based on Camshift. American Journal of Computational Mathematics, 6, 357-364. http://dx.doi.org/10.4236/ajcm.2016.64035
References
- 1. Brown, J.C., Pusey, P.N., Goodwin, J.W. and Ottewill, R.H. (1975) Light Scattering Study of Dynamic and Time Averaged Correlations in Dispersions of Charged Particles. Journal of Physics A: Mathematical and General, 8, 664-682.
- 2. Hayter, J.B. (1985) Physics of Amphiphiles: Micelles, Vesicles and Microemulsions. In: Degiorgio, V. and Corti, M., Eds., Proceeding of the International School of Physics, North Holland, Amsterdam, 59.
- 3. Pandey, R.K. (2014) Effect of Solvents on the Degree of Ionization of Polystyrene Balls and Their Liquid Crystallization in the Suspension Using Static Light Scattering Method. SOP Transactions on Physical Chemistry, 1, 29-40.
- 4. Alexander, S., Chaikin, P., Grant, P., Morales, G., Pincus, P. and Hone, D. (1984) Charge Renormalization, Osmotic Pressure and Bulk Modulus of Colloidal Crystals: Theory. The Journal of Chemical Physics, 80, 5776-5781.
http://dx.doi.org/10.1063/1.446600 - 5. Pandey, R.K. and Tripathi, D.N. (2010) Comparison of Structure Factors and Pair Correlation Functions Obtained Using Coulomb Attractive Potential and Screened Coulomb Potential for the Suspended Macroions. Indian Journal of Physics B, 84, 397-404.
http://dx.doi.org/10.1007/s12648-010-0024-0 - 6. Verwey, E.J.W. and Overbeek, J.Th.G. (1948) Theory of the Stability of Lyophobic Colloids: The Interaction of Sol Particles Having an Electric Double Layer. Elsevier, Amsterdam.
- 7. Tata, B.V.R., Kesavamoorthy, R. and Arora, A.K. (1986) Onrmsa Description of Liquid Order in Dilute Charged Colloidal Suspensions. Molecular Physics, 57, 369-378.
http://dx.doi.org/10.1080/00268978600100291 - 8. Pandey, R.K. and Tripathi, D.N. (2001) Schulz Distribution Function and the Polydispersity of the Binary Suspension of Charged Macroions. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 190, 217-227.
http://dx.doi.org/10.1016/S0927-7757(01)00707-5 - 9. Pandey, R.K. (2014) Comparison of Pair Correlation Functions Obtained Using SI and DLVO Potentials for the Ordered Plasmas. SOP Transactions on Theoretical Physics, 1, 101-109.
- 10. Pandey, R.K. (2014) Liquid Crystals in Spheroid Macroions and Spherocylindrical Biomacroions Suspended into Water Using Sogami-Ise Potential. SOP Transactions on Applied Physics, 1, 27-37.
- 11. Pandey, R.K. (1998) A Study of Ordering in Macroionic Suspension and Related Problems. Ph.D. Thesis, Banaras Hindu University, Varanasi.
- 12. Pandey, R.K. (2013) Ordering in Suspended Charged Particles. Lambert Academic Publishing, Saarbrücken.
- 13. Hayter, J.B. and Penfold, J. (1981) An Analytic Structure Factor for Macroion Solutions. Molecular Physics, 42, 109-118.
http://dx.doi.org/10.1080/00268978100100091 - 14. Hayter, J.B. and Hansen, J.P. (1982) A Rescaled Mean Spherical Approximation Structure Factor for Dilute Charged Colloidal Dispersion. Molecular Physics, 46, 651-656.
http://dx.doi.org/10.1080/00268978200101471 - 15. Pandey, R.K. and Tripathi, D.N. (1992) Rescaled Mean Spherical Approximation Structure Factor for an Aqueous Suspension of Polystyrene Spheres. Pramana Journal of Physics, 39, 589-595.
http://dx.doi.org/10.1007/BF02847278 - 16. Pandey, R.K. and Tripathi, D.N. (1995) Effect of Charge and Size on Ordering of Highly Charged Concentrated Macroions in Suspension. Pramana Journal of Physics, 44, 1-7.
http://dx.doi.org/10.1007/BF02898207 - 17. Härtl, W. and Versmold, H. (1984) Temperature Dependence of the Structure Factor S(Q) of Liquid-Like Ordered Colloidal Dispersions. The Journal of Chemical Physics, 81, 2507-2510.
http://dx.doi.org/10.1063/1.447911 - 18. Nagele, G., Medina-Noyola, M., Klein, R. and Arauz-Lara, J. (1988) Time-Dependent Self-Diffusion in Model Suspensions of Highly Charged Brownian Particles. Physica A: Statistical Mechanics and Its Applications, 149, 123-163.
- 19. Aguanno, B.D. and Klein, R. (1991) Structural Effects of Polydispersity in Charged Colloidal Dispersions. Journal of Chemical Society Faraday Transactions, 87, 379-390.
http://dx.doi.org/10.1039/ft9918700379 - 20. Ruiz-Estrada, H., Medina-Noyola, M. and Nagele, G. (1990) Rescaled Mean Spherical Approximation for Colloidal Mixtures. Physica A: Statistical Mechanics and Its Applications, 168, 919-941.
- 21. Krause, R., Nagele, G., Karrer, D., Schneider, J., Klein, R. and Weber, R. (1988) Structure and Self-Diffusion in Dilute Suspensions of Polystyrene Spheres: Experiment vs. Computer Simulation and Theory. Physica A: Statistical Mechanics and Its Applications, 153, 400-419.
- 22. Kesavamoorthy, R. and Arora, A.K. (1986) Elastic Constants of Colloidal Glass. Journal of Physics C: Solid State Physics, 19, 2833-2846.
- 23. Tata, B.V.R., Kesavamoorthy, R. and Sood, A.K. (1987) Structure Factor for a Two Component Mixture of Dilute Colloidal Suspensions. Molecular Physics, 61, 943-952.
http://dx.doi.org/10.1080/00268978700101571 - 24. Sood, A.K. (1987) Light Scattering from Colloids. Hyperfine Interactions, 37, 365-384.
http://dx.doi.org/10.1007/BF02395721 - 25. Ornstein, L.S. and Zernike, F. (1914) Accidental Deviations of Density and Opalescence at the Critical Point of a Single Substance. Proceeding of Akademic Science (Amsterdam), 17, 793-806.
- 26. Hayter, J.B. and Hansen, J.P. (1982) The Structure Factor of Charged Colloidal Dispersions at Any Density. Institut Laue-Langevin Report, No. 82HA14T.
- 27. Hayter, J.B. (1979) A Program for Fast Bi-Directional Transform between G(R) and S(Q). Institut Laue-Langevin Report, No. 79HA48S.
- 28. Schaefer, D.W. (1977) Colloidal Suspensions as Soft Core Liquids. The Journal of Chemical Physics, 66, 3980-3984.
http://dx.doi.org/10.1063/1.434449 - 29. Pieranski, P. (1983) Colloidal Crystals. Contemporary Physics, 24, 25-73.
http://dx.doi.org/10.1080/00107518308227471 - 30. Wagner, N.J., Krause, R., Rennie, A.R., Aguanno, B.D. and Goodwin, J. (1991) The Microstructure of Polydisperse, Charged Colloidal Suspensions by Light and Neutron Scattering. The Journal of Chemical Physics, 95, 494-508.
- 31. Pandey, R.K. (2014) Comparison of Structure Factors Obtained with Sogami-Ise Potential and DLVO Potential for H+-He++ Mixtures. SOP Transactions on Theoretical Physics, 1, 73-81.
- 32. Pandey, R.K. (2014) Structure Factor of Suspended Polystyrene Macroions Using Sogami-Ise Potential. Journal of Physics & Astronomy, 3, F67-F70.
- 33. Liu, H., Long, Y. and Zhang, C. (2015) A Mean-Shift Tracking Algorithm Based on Background Weighted Histogram. Journal of Hunan University of Technology, 29, 69-73.
- 34. Wang, Y., Cheng, H., Li, S. and Gao, C. (2016) Multi-Strategy Scale Adaptive Tracking Algorithm via Keypoint Matching. Computer Engineering and Design, 37, 247-253.
- 35. Wu, D., Cheng, W. and Yu, S. (2010) Camshift Object Tracking Algorithm Based on Inter-frame Difference and Motion Prediction. Opto-Electronic Engineering, 37, 55-60.
- 36. Xiu, C. and Wei, S. (2015) Camshift Tracking with Saliency Histogram. Optics and Precision Engineering, 23, 1749-1757.
https://doi.org/10.3788/OPE.20152306.1749 - 37. Karavasilis, V., Nikou, C. and Likas, A. (2011) Visual Tracking Using the Earth Mover’s Distance between Gaussian Mixtures and Kalman Filtering. Image and Vision Computing, 29, 395-305.
https://doi.org/10.1016/j.imavis.2010.12.002 - 38. Liu, S. and Jiang, X. (2010) A Moving Object Tracking Algorithm Based on Modified Camshift/Kalman Filter. Control Engineering of China, 17, 470-474.
- 39. Xia, J., Wu, J., Zhai, H. and Cui, Z. (2009) Moving Vehicle Tracking Based on Double Difference and Camshift. Proceedings of the 2009 International Symposium on Information Processing, Huangshan, 21-23 August 2009, 29-32.
- 40. Tang, Q., Dai, S.G. and Yang, J. (2013) Object Tracking Algorithm Based on Camshift Combining Background Subtraction with Three Frame Difference. In: Kim, Y.-H., Ed., Applied Mechanics and Materials, Trans Tech Publications Inc., Switzerland, 1116-1119.
https://doi.org/10.4028/www.scientific.net/amm.373-375.1116 - 41. Chen, J., Zhu, C. and Luo, B. (2015) A Combination of Camshift Algorithm and Brisk Feature Point for Real Time Moving Target Tracking. Journal of Chongqing University of Technology (Natural Science), 29, 112-119.
- 42. Wang, X., Yang, G. and Wu, S. (2016) An Improved Algorithm for Target Tracking Based on Camshift Algorithm and Kalman Filter. Industrial Control Computer, 29, 80-81.
- 43. KaewTraKulPong, P. and Bowden, R. (2002) An Improved Adaptive Background Mixture Model for Real-Time Tracking with Shadow Detection. In: Remagnino, P. and Jones, G.A., Eds., Computer Vision and Distributed Processing, Springer, New York, 135-144.
https://doi.org/10.1007/978-1-4615-0913-4_11 - 44. Hofmann, M., Tiefenbacher, P. and Rigoll, G. (2012) Background segmentation with feedback: The Pixel-Based Adaptive Segmenter. Proceedings of 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Rhode Island, 16-21 June 2012, 38-43.
- 45. Zuo, J., Liang, Y., Pan, Q., Zhao, C. and Zhang, H. (2008) Camshift Tracker Based on Multiple Color Distribution Models. Acta Automatica Sinica, 34, 736-742.
https://doi.org/10.3724/SP.J.1004.2008.00736 - 46. Yan, J., Chen, S. and Ai, S. (2014) Target Tracking with Improved CAMShift Based on Kalman Predictor. Journal of Chinese Inertial Technology, 22, 536-542.







