American Journal of Computational Mathematics
Vol.05 No.04(2015), Article ID:62267,10 pages
10.4236/ajcm.2015.54040
Dynamical Model with Application to the Analysis of the Sweet Spot on a Baseball Bat
Li Cheng, Zaiqiang Ku*
College of Mathematics and Physics, Huanggang Normal University, Huanggang, China

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 November 2015; accepted 25 December 2015; published 28 December 2015
ABSTRACT
In this paper, we analyze the effect on the ball-bat model of corking the bat, and investigate the relationship between the sweet spot and different materials. First and foremost, we develop a simple but effective theoretical model to give a rough estimate for the sweet spot of the bat. Second, we give a simplified abstract form of bat which facilitates the description and modeling study. Last but not least, according to different material caused rotary inertia and different recovery coefficient, researches on the different material hitting effect were made.
Keywords:
Baseball Bat, Sweet Spot, Dynamical Model, Finite Element

1. Introduction
Baseball, the national ball in USA and Japan, is popular and is thought as the combination of competition, wisdom, braveness and cooperation. Batters know from experience that there is a sweet spot on the baseball bat, about 17 cm from the end of the barrel, where the shock of the impact, felt by the hands, is reduced to such an extent that the batter is almost unaware of the collision (Bower [1] ). In addition to the popular book by Adair [2] , there have numerous papers which address a wide variety of issues amenable to a physics calculation. Notable experimental papers are those of Brody [3] , Cross [4] , Nicholls et al. [5] , King et al. [6] , Yee et al. [7] , and Smith [8] .
Whilst technology continues to flourish for the television audience, very few developments in batting equipment have occurred. One of the main reasons stems from the laws of cricket which limits the material composition of the cricket blade to wood. This is contrary to other sports such as tennis and squash where rackets have evolved significantly (Broe et al. [9] ; Chopp in [10] ) and numerous materials such as aluminums-based alloys, and titanium-based alloys have been utilized (Handee et al. [11] ; Bower and Sinclair [12] ). For research conducted on cricket bats, the main focus has been on modeling impacts and their vibration characteristics (Miller [13] ; Cross and Nathan [14] ). Very few studies appear to have investigated the actual impact between bat and ball (Stretch et al. [15] ), possibly due to the difficulty in accurately projecting the ball to the specified area on the bat.
Brody [3] studied the vibration spectrum of a hand-held bat during and after the collision and showed that the bat behaves as a free body on the short time scale of the collision. Cross [4] made an extensive study about the vibration spectrum of free and hand-held bats and concluded that there exists a zone of impact locations on the barrel end of the bat where the impact forces on the hands due to recoil and vibration are minimize.
After Brody [3] , Van [16] solved the problem to find the normal modes for transverse bending vibrations in the bat, applying the standard theory of beams, suitably modified for a non-uniform bat. Based on the investigations of Van [16] and Cross [4] [17] [18] , Nathan [19] proposed a model which developed for the collision between the baseball and bat, taking into account the transverse bending vibrations of the bat. Bower [1] investigated the sweet spot of atypical cricket bat in both the longitudinal and transverse direction for a low-impact velocity collision. Following the work of Nathan [19] , in this paper, we treat the sweet spot as the major study, analyze the effect on the ball-bat model of corking the bat, and investigate the relationship between the sweet spot and different materials.
This paper is organized as follows. In Section 2, we introduce some preliminary results. Section 3 makes some basic assumption for our modeling idea and gives the explanation of the symbols which will be used throughout the paper. In Section 4, we present a dynamical model to modeling the sweet spot on a baseball bat. Section 5 gives some extension models. We offer our conclusions in Section 6.
2. Preliminary
In order to indicate the origin of the baseball bats problem, the following preliminary are worth mentioning.
2.1. Engineering Concepts Relating to Baseball
Before discussing the performance of baseballs and baseball bats, a few engineering concepts are presented.
2.1.1. Coefficient of Restitution (COR)
The COR is used to quantify the elasticity or “liveliness” of the baseball as it strikes a stationary object, such as a baseball bat. It is a measure of how elastic or inelastic two bodies when they come into contact with each other and must be measured experimentally. The following is a brief derivation of the COR (William and Leroy [20] ).
As mentioned in William and Leroy’s book Engineering Mechanics: Dynamics, bodies A and B are given initial velocities, 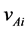 and
and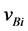 , respectively. As shown in Figure 1.
, respectively. As shown in Figure 1.
Assuming that non-impulsive force and the friction force between the two bodies may be neglected, the total momentum for the two bodies before (i) and after (f) the collision is conserved
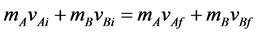 , (1)
, (1)
Figure 1. Two bodies in motion, before (top), during (middle) and after (bottom) acollision.
where 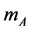 and
and 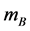 are masses of A and B, respectively.
are masses of A and B, respectively.
Considering the impulse forces acting on the individual bodies while the bodies are deforming during and after the collision, the coefficient of restitution e is defined as the ratio of the impulse during the collision and the impulse as the bodies is restored. It can be simplified as
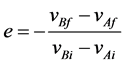 , (2)
, (2)
where the COR is the negative ratio of the relative velocities of two bodies after and before a collision.
The COR is not a value that is regarded as a material property because it not only depends on the material of both impacted bodies, but for nonlinear material systems. It also depends on the velocity at which they collide. It will also vary with respect to9different sizes, shapes and the temperature of the impacting bodies. For values of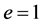 , the collision is considered to be a perfectly elastic impact, that is, there is no energy loss due to the deformation of the bodies at impact. For values of
, the collision is considered to be a perfectly elastic impact, that is, there is no energy loss due to the deformation of the bodies at impact. For values of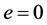 , the collision is considered to be a perfectly plastic impact. The relative velocity of the two bodies after impact is zero and the two particles move together at the same speed (Mustone [21] ).
, the collision is considered to be a perfectly plastic impact. The relative velocity of the two bodies after impact is zero and the two particles move together at the same speed (Mustone [21] ).
2.1.2. Mass Moment of Inertia and Parallel Axis Theorem
The mass moment of inertia is a measure of a body to resist a rotational acceleration about an axis and is the best measure of how easily a bat can be swung. It is simply denoted as MOI, noting that it refers to the mass moment of inertia and not to be confused with an area moment of inertia. Studies described later have shown that battedball velocity increases with increasing bat swing speed. Therefore, the MOI, can provide one measure of bat performance (Mustone [21] ) because it is an indicator of swing speed.
2.1.3. The Sweet Spot
Trying to locate the exact sweet spot on a baseball or softball bat is not as simple a task as it might seem, because there are a multitude of definitions of the sweet spot (Russell [22] ):
1) The location which produces least vibration sensation (sting) in the batter’s hands;
2) The location which produces maximum batted ball speed;
3) The location where maximum energy is transferred to the ball;
4) The location where coefficient of restitution is maximum;
5) The center of percussion;
6) The node of the fundamental vibration mode;
7) The region between nodes of the first two vibration modes;
8) The region between center of percussion and node of first vibration, mode.
In the paper, we define “the sweet spot” as the region where the ball gets the maximum exit speed.
2.2. Wood and Metal
The physical differences between wood and metal baseball bats are quite obvious. A wood bat is solid but not very durable. A metal (usually aluminum) bat on the other hand, is hollow and more durable than wood. A significant difference between wood and metal bats is the energy-transfer mechanism between the bat and the baseball during the collision. The difference between the energy-transfer mechanisms is a fundamental result of the wood bat being solid and the metal bat being hollow.
3. Basic Assumption and Symbols
We make the following two assumptions, which have been used extensively in Smith [8] and Yee et al. [7] .
1) Ignore the impact of hand on the ball. Studies have shown that the impact of hand on the ball is slight at the moment of impact. So the bat can be approximated as a “free end”.
2) When the bat hits the ball, direction of the ball velocity and the axis of the bat are orthogonal. Hence, the impact of friction between the ball and bat can be ignored.
Before constructing a dynamical model for sweet spot on a baseball bat problem, let us introduce the following notations, parameters and decision variables used in this paper.
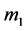 : the mass of the ball;
: the mass of the ball;
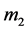 : the mass of the bat;
: the mass of the bat;
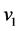 : the initial velocity of the ball;
: the initial velocity of the ball;
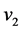 : the velocity of the ball after collision;
: the velocity of the ball after collision;
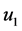 : the velocity of the ball-centroid before collision;
: the velocity of the ball-centroid before collision;
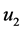 : the velocity of the ball-centroid after collision;
: the velocity of the ball-centroid after collision;



4. Dynamical Model
4.1. Theoretical Models for the Sweet Spot
Known from the analysis of the batter’s movements, there are two rotation systems. One is the rotation of arm and the bat to body gravity as the axis. And the other is the rotation of the bat to wrist as the axis. Specific steps of this model are described as follows:
Step 1 Take the body gravity B as the origin of coordinates, and take the axis of the bat as the X-axis, the perpendicular direction of the X-axis as the Y-axis. Then aplane rectangular coordinate system is established.
Step 2 Formulate that center-of-mass coordinate of the bat is C, coordinate of body centre-of-gravity is B, and the coordinate of hand-held point is W, the coordinate of hit point is P, the coordinate of knob end is
Step 3 At the moment of collision, the force between bat and ball is greater than their own weights and hand upward force. Therefore, with the ball-bat system as the research object, there is momentum conservation on the Y-axis, which can be formulated as

where 





Step 4 Assuming that the angular velocity before and after collision are 


As the preliminary in subsection

Step 5 Establish angular momentum conservation equation of ball-bat system to the body gravity as the axis, as follows

Step 6 From Equations (3) to (6), the expression of 

where J is the moment of inertia and the expression of J is

Finally the derivation of 

The solution of 
4.2. Data Verification
The general specification of wood baseball bat is shown in Table 1.
As a rotating body, the cross-section along the X-axis, where the length of



Based on the definition of centre-of-gravity, the moment of inertia is balance at two sides of it. So the following equation was attained.
where r is an integral function of the variable x.
The length of 0.6423 and 0.3459 are measured for 

By using MATLAB, a figure reflecting the relationship of the ball exit velocity and the hitting spot is obtained (Figure 2). The conclusion drawn from Figure 2 is that the peak of the curve is the coordinates of the sweet spot. So the distance from the sweet spot to the knob end of the bat is 0.7840 m. This just explains why this spot isn’t at the end of the bat.
4.3. Analysis of “Corking” a Bat
No doubt, “corking” a bat would change a series of physical properties of the bat, such as the bat mass, the centre-of-gravity position, and the coefficient of restitution, etc. The change of these physical properties will ultimately affect the hitters’ levels of technology, which is related to the fairness of the game directly. The specific
Table 1. Physical parameter of wood bat.
Figure 2. The relationship of the ball exit velocity and the hitting spot.
steps of this model are described as follows.
According to practical experience, the cork is usually a cylinder which diameter is 1 inch (2.54 cm) and depth is 10 inch (25.4 cm). The density of the cork is
1) The mass and inertia of the bat deceases, and the bat control enhances.
2) Centre-of-gravity position is closer to the knob end than before, so that the ball angular momentum decreases. Then the result is affected.
3) The moment of inertia decreases. Then, the sweet spot and the maximum velocity are affected.
The following are three aspects of quantitative analysis from the above filler effect on the ball.
1) Reduction of the mass

2) Variation of the centre-of-gravity position

In the coordinate system, original X-coordination of centre-of-gravity is

3) Reduction of the moment of inertia

where 

Based on the dynamical model, the sweet spot and maximum velocity of the corking bat can be attained only by correcting the moment of inertia. Namely

After substituting the superior limit of the corking bat’s density (
Figure 3 is a comparison of the normal bat and the corking bat. The X-axis is the distance to the body centre-of-gravity, and the Y-axis is the exit speed of the ball.
The conclusion can be drawn from Figure 3 that corking a bat can’t enhance the “sweet spot” effect. The major reason is that the moment of inertia decreases due to the decrease of the bat mass, so that the energytransferred decreases. This results in the decrease of the exit speed directly. Whereas, the superiority of the corking bat mainly reflects in the good control ability to the bat and the great acceleration, so the reaction time is lengthened. This is also the reason that major league baseball prohibits “corking”.
4.4. Bat on the Ball with Different Material
Based on the preliminary in subsection 2.2, there are two major differences between a wood bat and an aluminum bat. One is the difference of moment of inertia leaded by the difference of density and mass. The other is the coefficient of restitution leaded by the difference of metal.
Assuming that the shape of the aluminum bat is the same to the wood bat we use before, the dynamical model can be used. We define v as the exit velocity of the aluminum bat and x as the distance from coordination of the hitting spot. Analyzing from aspects of the moment of inertia and recovery coefficient, the expression of the relationship between v and x is as follows,

Accessing to relevant information (Greenwald, Penna, and Crisco [23] ), the moment of inertia of the aluminum bat is 3.2256. Using the dynamical model, a relationship graph is obtained (Figure 3).
The modeling results show that roughly aluminum bats have higher batted ball speed than wooden bats. The purpose is to enhance athletic baseball player’s own fitness and skill, rather than engage in competition sports equipment, so the competition is not allowed to use the metal bats.
5. Model Extension
In the dynamical model, we didn’t take the energy loss into consideration, which is not match with the actual. Here we give a model extension to analyze the energy loss.
The main factor of energy loss at the collision process is vibration of the ball. Therefore, energy loss of this part should be minimized. The region between the free vibration and the fundamental nodes of the second harmonic is where the vibration energy transfer is the smallest. In the model, the free vibration of the bat is analyzed
Figure 3. Comparison of normal wood bat and aluminum bat.
based on the beam vibration model (Mustone [21] ). And finite element analysis is used to calculate the vibration parameters of a baseball bat.
5.1. Beam Vibration Model
The following is the analysis of the process of free vibration of the bat based on the beam vibration model. We mainly analyze the transfer of the fundamental harmonic, the second harmonic and the third harmonic to find the smallest vibration area. In the process of hitting, the bat is not subject to the torque and vertical extrusion pressure, so that the longitudinal vibration and tensional vibration are neglected. So the baseball is simplified as the balanced-distributed bat, which is shown in Figure 4.
The wave equation of the transverse vibration is as follows:

where 

The boundary conditions are as follows:

Then the following expressions are formed,
Define the function

Assuming that

Then the expression of amplitude Y is formed,

5.2. Finite Element Analysis
The real bat is irregular. In order to well simulate the vibration energy’s transmission in a real bat, finite element analysis can be used based on the above beam vibration model. Using this method, we can refine model and decompose it into a series of beam vibration model. Substitute into the equations in above beam vibration model, we can take it for a series of beam vibration’s superposition. On the basis of the existing data, we will substitute the data into the sixth equations, then make corresponding harmonic figure in MATLAB. Meanwhile, we can find out the first three vibration mode’s frequency from it. They are classified as

Finally, the image of previous three waves of vibration can be made in MATLAB as follows (Figure 5). From Figure 5, we can see that the ball hitting at zero point won’t cause the corresponding mode vibration. In order to
Figure 4. Simplified model.
Figure 5. Image of previous three waves of vibration.
make the total vibration energy lost as little as possible, we make a comprehensive consideration of the first three vibration and put the optimal hit region defined as the scope between the base wave’s first node and the second harmonic first nodes, denoted as (0.7652, 0.8012). In this area, the vibration amplitude caused by hitting uniform stem is smaller. We can conclude that the sweet point determined by the dynamical model is reasonable and faithful.
6. Concluding Remarks
In this paper, we analyzed the effect on the ball-bat model of corking the bat and also studied the relationship between the sweet spot and different materials. Our substantive contributions are threefold. First and foremost, we developed a simple but effective theoretical model to give a rough estimate for the sweet spot of the bat. Secondly, a simplified abstract form of the bat is given which makes description and modeling study easy. Last but not least, because different material caused rotary inertia and different recovery coefficient, researches on the different material hitting effect were made.
There are several weaknesses of this study. Firstly, in order to make the process of solving the inertia easy, we treat the aluminum bat as a solid body. But it’s hollow in practice that may leads to the error of exit velocity of the ball. Secondly, we define that the direction of the ball velocity and the axis of the bat are orthogonal. However, it can’t be always like that. So the model can’t apply in any situation. These and other related drawbacks await future research.
Acknowledgements
This work was supported by the Key Project of Hubei Provincial Natural Science Foundation under Grant No. 2015CFA144.
Cite this paper
LiCheng,ZaiqiangKu, (2015) Dynamical Model with Application to the Analysis of the Sweet Spot on a Baseball Bat. American Journal of Computational Mathematics,05,458-467. doi: 10.4236/ajcm.2015.54040
References
- 1. Adair, R.K. (1994) The Physics of Baseball. HarperCollins, New York.
- 2. Brody, H. (1990) Models of Baseball Bats. American Journal of Physics, 58, 756-758.
http://dx.doi.org/10.1119/1.16378 - 3. Bower, R.G. (2012) The Sweet Spot of a Cricket Bat for Low Speed Impacts. Sports Engineering, 15, 53-60.
http://dx.doi.org/10.1007/s12283-012-0087-6 - 4. Bower, R.G. and Sinclair, P. (2007) Tennis Racket Stiffness, String Tension and Impact Velocity Effects on Post-Impact Ball Angularvelocity. Sports Engineering, 10, 111-122.
http://dx.doi.org/10.1007/BF02844208 - 5. Broe, M., Sherwood, J. and Drane, P. (2010) Experimental Study of the Evolution of Composite Baseball Bat Performance. Procedia Engineering, 2, 2653-2658.
http://dx.doi.org/10.1016/j.proeng.2010.04.047 - 6. Choppin, S. (2013) An Investigation into the Power Point in Tennis. Sports Engineering, 16, 173-180.
- 7. Cross, R. (1998) The Sweet Spot of a Baseball Bat. American Journal of Physics, 66, 772-779.
http://dx.doi.org/10.1119/1.19030 - 8. Cross, R. (2011) Physics of Baseball and Softball. Springer, New York.
- 9. Cross, R. (2014) Impact of Sports Balls with Striking Implements. Sports Engineering, 17, 3-22.
http://dx.doi.org/10.1007/s12283-013-0132-0 - 10. Cross, R. and Nathan, A. (2009) Performance versus Moment of Inertia of Sporting Implements. Sports Technology, 2, 7-15.
http://dx.doi.org/10.1002/jst.88 - 11. Greenwald, R.M., Penna, L.H. and Crisco, J.J. (2001) Differences in Batted Ball Speed with Wood and Aluminum Baseball Bats: A Batting Cage Study. Journal of Applied Biomechanics, 17, 241-252.
- 12. Handee, S.P., Greenwald, R.M. and Crisco, J.J. (1998) Static and Dynamic Properties of Various Baseballs. Journal of Applied Biomechanics, 14, 390-400.
- 13. King, K., Hough, J., McGinnis, R. and Perkins, N.C. (2012) A New Technology for Resolving the Dynamics of a Swinging Bat. Sports Engineering, 15, 41-52.
http://dx.doi.org/10.1007/s12283-012-0084-9 - 14. Miller, S. (2006) Modern Tennis Rackets, Balls and Surfaces. British Journal of Sports Medicine, 40, 401-405.
http://dx.doi.org/10.1136/bjsm.2005.023283 - 15. Mustone, T.J. (1996) A Method to Evaluate and Predict the Performance of Baseball Bats Using Finite Elements. University of Massachusetts, Lowell.
- 16. Nathan, A.M. (2000) Dynamics of the Baseball-Bat Collision. American Journal of Physics, 68, 979-990.
- 17. Nicholls, R.L., Miller, K. and Elliott, B.C. (2006) Numerical Analysis of Maximal Bat Performance in Baseball. Journal of Biomechanics, 39, 1001-1009.
http://dx.doi.org/10.1016/j.jbiomech.2005.02.020 - 18. Russell, D.A. (2004) Physics and Acoustics of Baseball & Softball Bats. PhD Thesis, Science & Mathematics Department, Kettering University, Flint.
- 19. Smith, L.V. (2014) Hygrothermal Effects of Baseballs and Softballs. Sports Engineering, 17, 123-130.
http://dx.doi.org/10.1007/s12283-013-0143-x - 20. Stretch, R., Brink, A. and Hugo, J. (2005) A Comparison of the Ball Rebound Characteristics of Wooden and Composite Cricket Bats at Three Approach Speeds. Sports Biomechanics, 4, 37-45.
http://dx.doi.org/10.1080/14763140508522850 - 21. Van, Z.L. (1992) The Dynamical Theory of the Baseball Bat. American Journal of Physics, 60, 172-181.
http://dx.doi.org/10.1119/1.16939 - 22. William, F. and Leroy, D. (1993) Engineering Mechanics: Dynamics. John Wiley and Sons, New York.
- 23. Yee, J., Sherwood, J.A. and Fitzgerald, S. (2014) Batted-Ball Performance of a Composite Softball Bat as a Function of Ball Type. Procedia Engineering, 72, 465-470.
http://dx.doi.org/10.1016/j.proeng.2014.06.081
NOTES
*Corresponding author.












