Received 14 March 2015; accepted 22 May 2015; published 25 May 2015

ABSTRACT

Dislocated metric space differs from metric space for a property that self distance of a point needs not to be equal to zero. This property plays an important role to deal with the problems of various disciplines to obtain fixed point results. In this article, we establish a common fixed point theorem for two pairs of weakly compatible mappings which generalize and extend the result of Brain Fisher [1] in the setting of dislocated metric space with replacement of contractive constant by contractive modulus for which continuity of mappings is not necessary and compatible mappings by weakly compatible mappings.

Keywords:

d-Metric Space, Common Fixed Point, Weakly Compatible, Contractive Modulus, Cauchy Sequence

1. Introduction

In 1922, S. Banach [2] established a fixed point theorem for contraction mapping in metric space. Since then a number of fixed point theorems have been proved by many authors and various generalizations of this theorem have been established. In 1982, S. Sessa [3] introduced the concept of weakly commuting maps and G. Jungck [4] in 1986, initiated the concept of compatibility. In 1998, Jungck and Rhoades [5] initiated the notion of weakly compatible maps and pointed that compatible maps were weakly compatible but not conversely.

The study of common fixed point of mappings satisfying contractive type conditions has been a very active field of research activity. In 1986, S. G. Matthews [6] introduced the concept of dislocated metric space under the name of metric domains in domain theory. In 2000, P. Hitzler and A. K. Seda [7] generalized the famous Banach Contraction Principle in dislocated metric space. The study of dislocated metric plays very important role in topology, logic programming and in electronics engineering.

The purpose of this article is to establish a common fixed point theorem for two pairs of weakly compatible mappings in dislocated metric spaces which generalize and improve similar results of fixed point in the literature.

2. Preliminaries

We start with the following definitions, lemmas and theorems.

Definition 1. [7] Let X be a non empty set and let 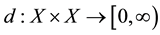be a function satisfying the following conditions:

1).

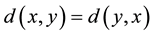2) 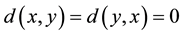implies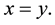

3) 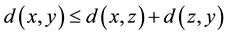for all.

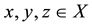Then d is called dislocated metric (or d-metric) on X and the pair 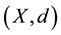is called the dislocated metric space (or d-metric space).

Definition 2. [7] A sequence 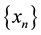in a d-metric space 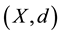is called a Cauchy sequence if for given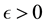, there corresponds 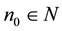such that for all 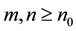, we have.

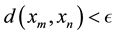Definition 3. [7] A sequence in d-metric space converges with respect to d (or in d) if there exists 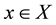such that 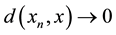as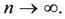

In this case, x is called limit of (in d)and we write

Definition 4. [7] A d-metric space is called complete if every Cauchy sequence in it is convergent with respect to d.

Definition 5. [7] Let be a d-metric space. A map is called contraction if there exists a number with such that

We state the following lemmas without proof.

Lemma 1. Let be a d-metric space. If is a contraction function, then is a Cauchy sequence for each

Lemma 2. [7] Limits in a d-metric space are unique.

Theorem 1. [7] Let be a complete d-metric space and let be a contraction mapping, then T has a unique fixed point.

Definition 6. Let A and S be two self mappings on a set X. Mappings A and S are said to be commuting if .

Definition 7. Let A and S be two self mappings on a set X. If for some, then x is called coincidence point of A and S.

Definition 8. [5] Let A and S be mappings from a metric space into itself. Then, A and S are said to be weakly compatible if they commute at their coincident point; that is, for some implies

Definition 9. A function is said to be contractive modulus if for

Definition 10. A real valued function defined on is said to be upper semicontinuous if

for every sequence with as

It is clear that every continuous function is upper semicontinuous but converse may not be true.

In 1983, B. Fisher [1] established the following theorem in metric space.

Theorem 2. Suppose that S, P, T and Q are four self maps of a complete metric space (X, d) satisfying the following conditions

1) and.

2) Pairs (S, P) and (T, Q) are commuting.

3) One of S, P, T and Q is continuous.

4) where for all and

Then S, P, T and Q have a unique common fixed point. Also, z is the unique common fixed point of pairs (S, P) and (T, Q).

3. Main Results

Theorem 3. Let (X, d) be a complete d-metric space. Suppose that A, B, S and T are four self mappings of X satisfying the following conditions

i)

ii) where is an upper semicontinuous contractive modulus and

iii) The pairs and are weakly compatible, then A, B, S and T have an unique common fixed point.

Proof. Let be an arbitrary point of X and define a sequence in X such that

Now by condition ii), we have

where

is not possible since is a contractive modulus, so

(1)

Since is upper semicontinuous, contractive modulus the Equation (1) implies that the sequence is monotonic decreasing and continuous.

Hence there exists a real number such that

Taking limit in (1) we obtain which is possible if, sice is contractive modulus. therfore

We claim that is a cauchy sequence.

if possible, let is not a cauchy sequence. Then there exists a real number and subsequences and such that and

(2)

so that

Hence

Now

Taking limit as we have

So by contractive condition ii) and (2)

(3)

where

Now taking limit as we get

Therefore from (3) we have which is a contradiction, since is contractive modulus.

Hence is a cauchy sequence.

Since X is complete, there exists a point u in X such that. So,

Hence,

Since there exists a point such that. Now by condition ii)

where

Taking limit as we have

Thus implies which is a contradiction, since is a contractive modulus. Thus. Hence which represents that v is the coincidence point of A and S.

Since the pair are weakly compatible, so

Again, since there exists a point such that. Then by condition ii) we have,

where

If then which implies

a contradiction, since is a contractive modulus.

Again if then

a contradiction. Hence, Which implies. Therefore. Thus w is the coinci- dence point of B and T.

Since the pair are weakly compatible, so. Now we show that u is the fixed point of S.

By condition ii), we have

where,

If then,

a contradiction since is contractive modulus.

If or, one can observe that there are contradictions for both cases. Hence we conclude that which implies that

Therefore,

Now we show that u is the fixed point of T. Again by condition ii),

where,

If then,

a contradiction.

If or one can observe that there are contradictions for both cases. Hence we conclude that which implies that

Therefore

Hence, i.e. u is the common fixed point of the mappings and T.

Uniqueness:

If possible let u and z are two common fixed points of the mappings and T. By condition ii) we have,

where,

If then,

a contradiction, since is a contractive modulus.

Again if or one can observe that there are contradictions for both cases. Hence we conclude that which implies that

Therefore, u is the unique common fixed point of the four mappings and T. This completes the proof of the theorem.

Now we have the following corollaries:

Corollary 1. Let (X, d) be a complete dislocated metric space. Suppose that A, S and T are three self map- pings of X satisfying the following conditions:

1) and.

2) where is an upper semicontinuous contractive modulus and

.

3) The pairs and are weakly compatible, then A, S and T have an unique common fixed point.

Proof. If we take in theorem (3) and follow the similar proof we get the required result.

Corollary 2. Let (X, d) be a complete dislocated metric space. Suppose that A and S are two self mappings of X satisfying the following conditions.

1).

2) where is an upper semicontinuous contractive modulus and

.

3) The pair is weakly compatible, then A and S have an unique common fixed point.

Proof. If we take and in theorem (3) and follow the similar proof we get the required result.

Corollary 3. Let (X, d) be a complete dislocated metric space. Suppose that S and T are two self mappings of X satisfying the following conditions

1) where is an upper semicontinuous contractive modulus and

.

2) The pairs and are weakly compatible, then S and T have an unique common fixed point.

Proof. If we take in theorem (3) and follow the similar proof we get the required result.

Corollary 4 Let (X, d) be a complete dislocated metric space. Let be a map satisfying the following conditions

where is an upper semicontinuous contractive modulus and

then the map S has a unique fixed point.

Proof. If we take in corollary (3) and follow the similar proof we get the required result.

References