American Journal of Computational Mathematics
Vol.3 No.1(2013), Article ID:29114,5 pages DOI:10.4236/ajcm.2013.31006
Semi Numerical Solution for a Boundary Value Problem
1Department of Mathematics, Manipal Institute of Technology, Manipal University, Manipal, India
2Government First Grade College, Yellapur, India
Email: *nppaimit@yahoo.co.in, nnkatagi@yahoo.com, ckrishna2002@yahoo.com
Received October 29, 2012; revised December 9, 2012; accepted December 22, 2012
Keywords: Computer Extended Series; Domb-Sykes Plot; Pade’ Approximants; Polynomial Coefficients
ABSTRACT
The flow of viscous incompressible fluid through a tube is considered. The similarity transformation is used to reduce the governing equations into nonlinear ordinary differential equation. The solution procedure includes application of long series analysis with polynomial coefficients. The series representing physical parameters ( ,
,  ) reveal qualitative features which are comparable to pure numerical results. The analysis enables in extending region of validity. A complete description of the solutions is presented.
) reveal qualitative features which are comparable to pure numerical results. The analysis enables in extending region of validity. A complete description of the solutions is presented.
1. Introduction
Unsteady flows produced by a simple contraction or expansion of the wall have wide applications, for example, in physiological pumps, peristaltic motion Jafrin [1] problems involving collapsible tubes etc. Bertram et al. [2]. The unsteady flow of a viscous fluid produced by contraction of the walls of a vessel with one end closed has applications to:
1) Flow through a thin veins where the flow is controlled by a valve system;
2) Flow in coronary arteries which are subjected to a varying external pressure.
Secomb [3] extended the analysis of earlier authors for the channel with pulsating walls.
The field of computational fluid dynamics demands innovative new methods for the flow conditions. The explosive growth of numerical algorithms and easy access to bigger and faster computers are keeping in phase with each other. The expressions of the theoretical physicists and others are presenting new scenarios and novel methods in harnessing the remarkable power of digital computers. One method in this class is the semi-analytical semi numerical technique of computer extended series solution. Van Dyke [4] pioneered the use of long series analysis in fluid dynamics. In an earlier study Bujurke et al. [5] also successfully used this method.
In this paper, we investigate the problem of unsteady flow in contracting or expanding pipe, studied by Skalak and Wang [6] using long series methods. This problem Figure 1 for some particular choice of a(t), admits similarity transformation leading to a nonlinear differential equation. The initial approximations enable us, in proposing a series expansion with polynomial coefficients to calculate enough terms (universal coefficients) by computer. Using a Domb-Sykes plot we find the nature and location of singularity restricting the convergence of the singularity. Then the problem is also analysed using Pade’ approximants and other useful techniques.
2. Mathematical Formulation
Let the inside tube be prescribed by a(t). The NavierStokes equations then admit similarity solutions if
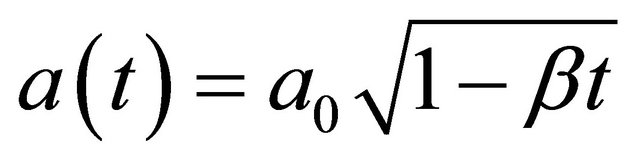 (2.1)
(2.1)
where  and
and  are constants.
are constants.
Let u and v be the velocities in cylindrical polar coordinate system in the directions of z and r respectively. Then the following transformations
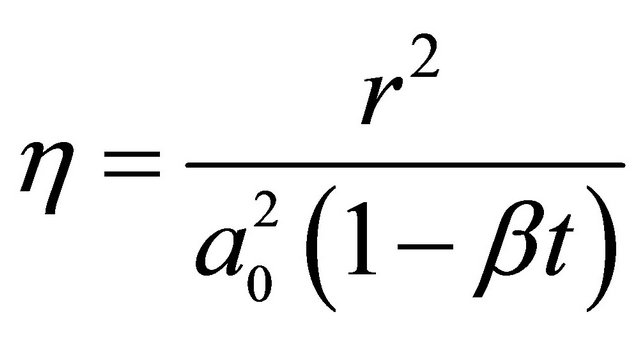 (2.2)
(2.2)
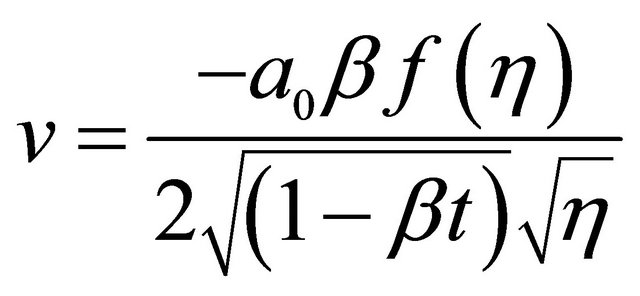 (2.3)
(2.3)
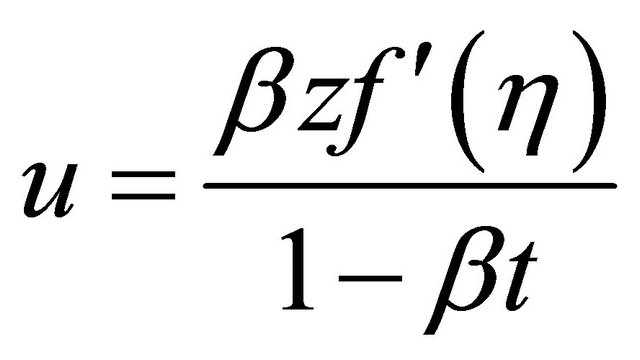 (2.4)
(2.4)
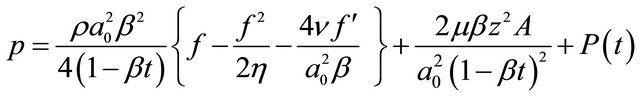 (2.5)
(2.5)
where 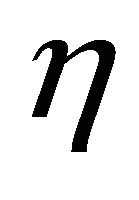 is normalized radius, p is the pressure,
is normalized radius, p is the pressure,  density,
density,  Kinematic viscosity. The constant A and the
Kinematic viscosity. The constant A and the
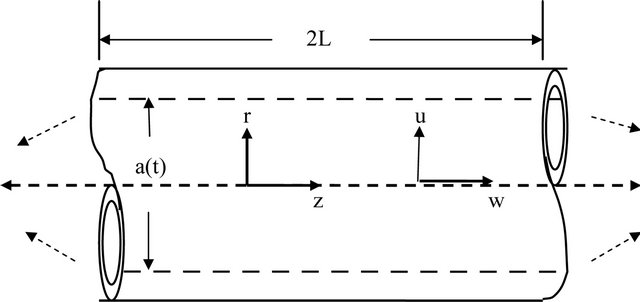
Figure 1. The coordinate axes.
function 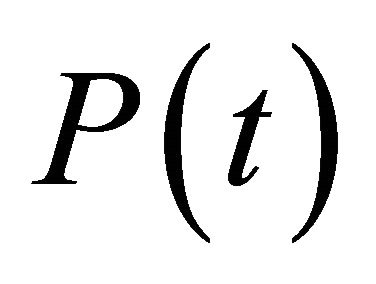 are to be determined from the boundary conditions.
are to be determined from the boundary conditions.
The boundary conditions are on
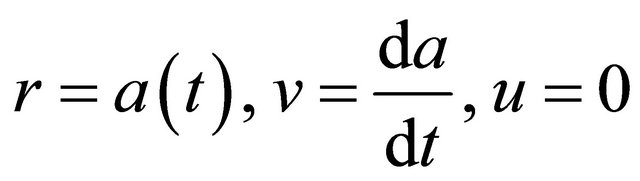 , (2.6)
, (2.6)
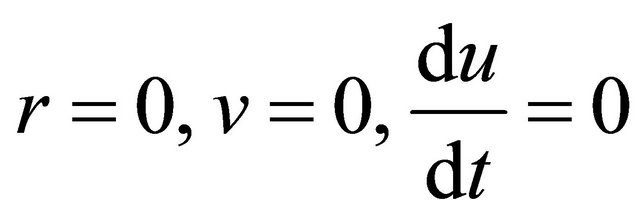 (2.7)
(2.7)
Using above equations, the Navier-Stokes equations take the form
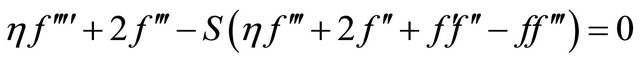 (2.8)
(2.8)
with the boundary conditions
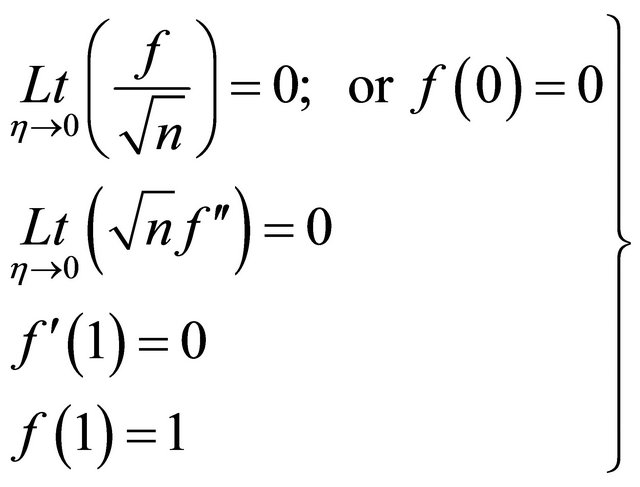 (2.9)
(2.9)
Here S is a squeeze number defined by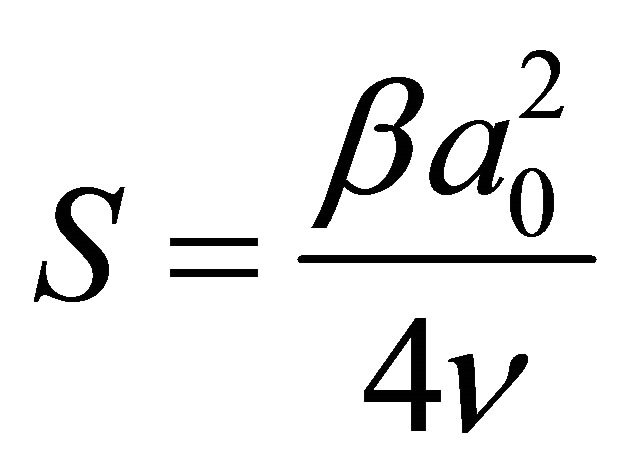 .
.
3. Method of Solution
We seek the solution of (2.8) in power series of S in the form
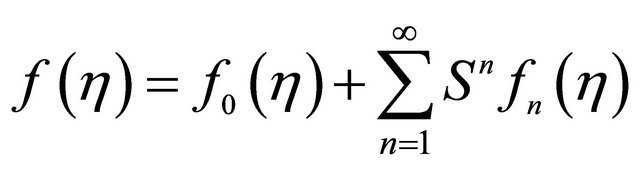 (3.1)
(3.1)
Substituting (3.1) into (2.8) and equating the like powers of S on both sides, we get
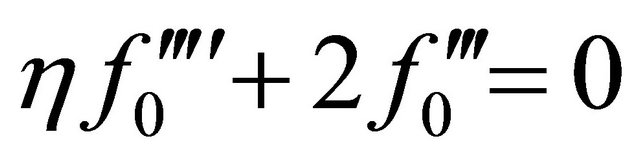 (3.2)
(3.2)
and
 (3.3)
(3.3)
The relevant boundary conditions take the forms
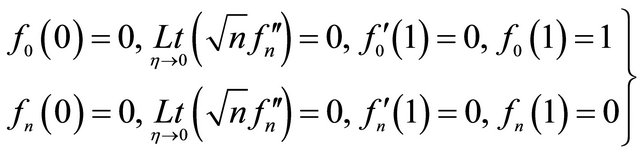 (3.4)
(3.4)
The solutions of the above equations up to 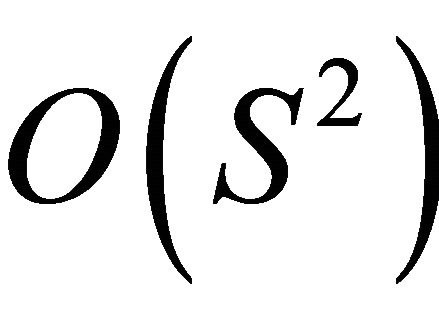 are
are
 (3.5)
(3.5)
4. Computer Extended Series
As the series (3.5) is slowly converging it is not reliable to analyze the problem accurately with just few terms. It is essential to get higher approximations. As one proceeds to higher approximations the algebra becomes cumbersome and it is difficult to calculate the terms manually. We propose a systematic series with polynomial coefficients which is quite useful and efficient in the calculation of higher approximations. In this method we get analytic structure of the solution just by generating universal coefficients. The series (3.5) gives solution for only up to S = 0.9. The forms of polynomial solutions (3.5) and nature of boundary conditions (3.4) suggest form of 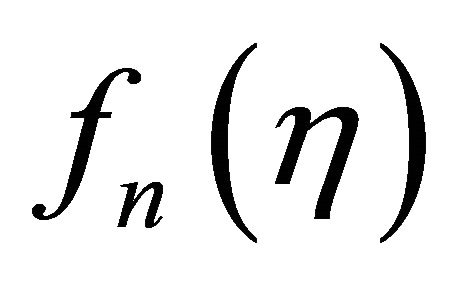 to be of the form
to be of the form
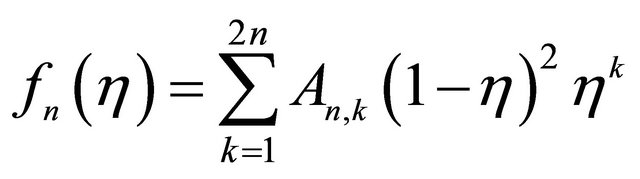 (4.1)
(4.1)
on substituting (4.1) into (3.3) and equating the coefficients of various powers of 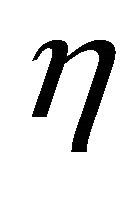 on both sides we get recurrence relation
on both sides we get recurrence relation 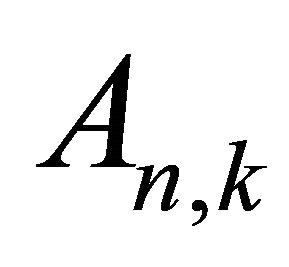 in the form
in the form
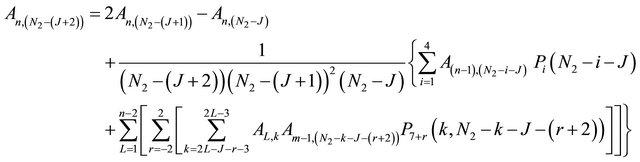 (4.2)
(4.2)
where , m = n – L and J varies from
, m = n – L and J varies from .
.

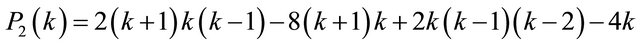




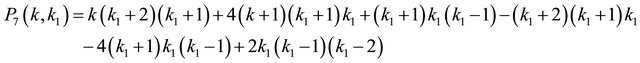


and 
The expression for 
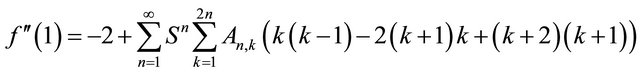 (4.3)
(4.3)
The expression for 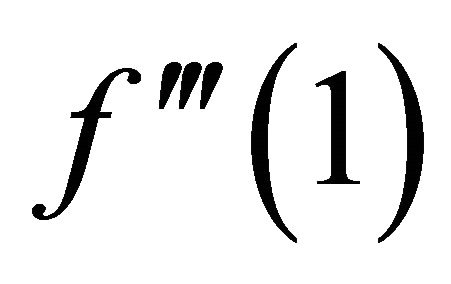
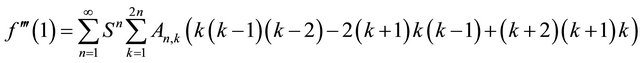 (4.4)
(4.4)
The relation (4.3) and (4.4) represents the shear stress and pressure gradient respectively. Domb-Sykes plot (Figures 2 and 3), after extrapolation Vandyke [7], confirms the radius of convergence of the series (4.3) and (4.4) to be  = 0.98 & 0.97 respectively. The region of validity of the above series increased by considering Pade’ sum which are given in Tables 1 and 2.
= 0.98 & 0.97 respectively. The region of validity of the above series increased by considering Pade’ sum which are given in Tables 1 and 2.
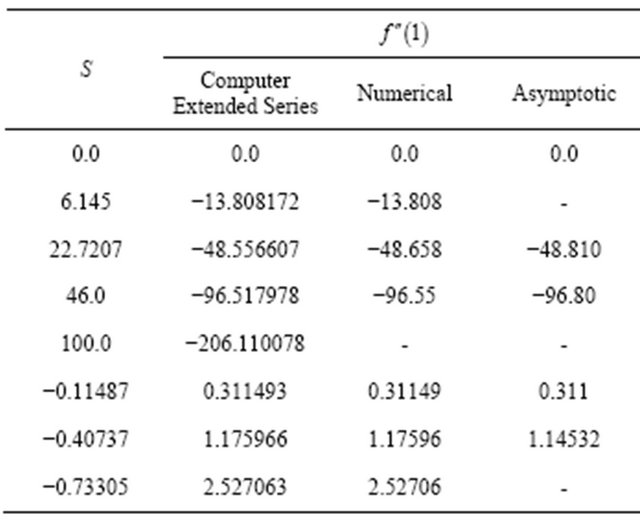
Table 1. Comparison of results for  obtained by various methods for different S.
obtained by various methods for different S.
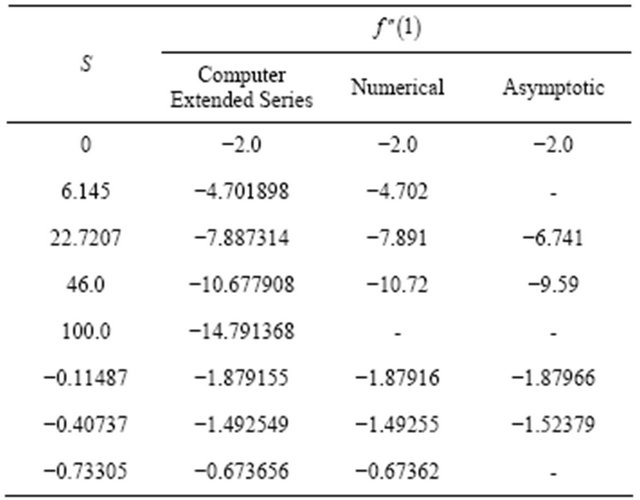
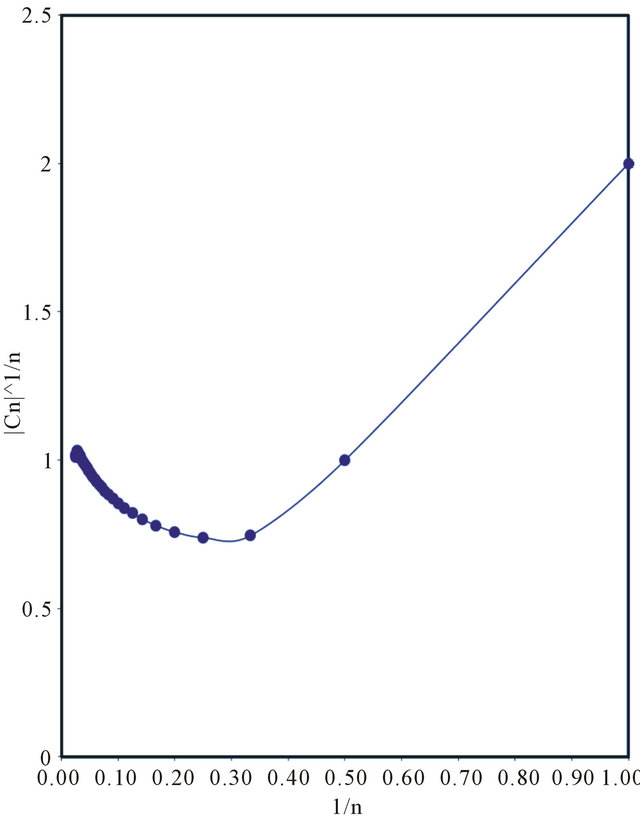
Figure 2kes plot for the coefficients of 4.3.

Figure 3. Domb-sykes plot for the coefficients of 4.4.
Table 2. Comparison of results for  obtained by various methods for different S.
obtained by various methods for different S.
5. Conclusion
A new type of series is presented for studying the problem of unsteady flow produced by squeezing of viscous fluid from a tube. Using recurrence relation (4.2) we generate universal coefficients (An,k,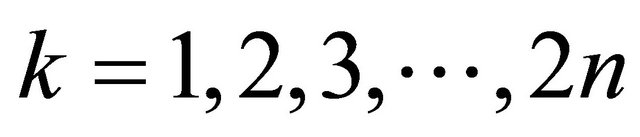 ;
;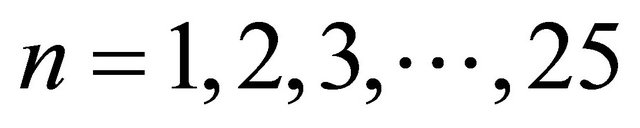 ). These coefficients in turn give universal polynomial functions fn(η)
). These coefficients in turn give universal polynomial functions fn(η)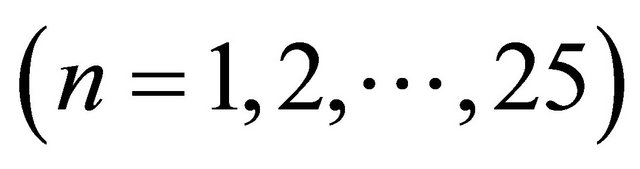 . The series (4.3) gives
. The series (4.3) gives  and (4.4) represents
and (4.4) represents  have random sign pattern. Using Domb-Sykes plot (Figures 2 and 3), we locate the position ad identifying the nature of the nearest singularity of the series restricting the convergence. The series (4.3) and (4.4) are summed using Pade’ approximants Bender and Orszag [8]. Earlier series solution results were only for small value of S. But we are able to go upto S = 100 using Pade’ approximants. The results are in very close agreement with the numerical findings Skalak and Wang [6].
have random sign pattern. Using Domb-Sykes plot (Figures 2 and 3), we locate the position ad identifying the nature of the nearest singularity of the series restricting the convergence. The series (4.3) and (4.4) are summed using Pade’ approximants Bender and Orszag [8]. Earlier series solution results were only for small value of S. But we are able to go upto S = 100 using Pade’ approximants. The results are in very close agreement with the numerical findings Skalak and Wang [6].
6. Acknowledgements
The research is supported by Manipal Academy of Higher Education, Manipal. (Under R & D scheme of M. I. T., Manipal) and one of us (KBC) wishes to thank the higher authority of Department of Collegiate Education, Govt. of Karnataka for their encouragement and support.
REFERENCES
- M. Y. Jaffrin and A. H. Shapiro, “Peristatic Pumping,” Annual Review of Fluid Mechanics, Vol. 3, 1971, pp. 13- 36. doi:10.1146/annurev.fl.03.010171.000305
- C. D. Bertram, C. J. Reymond and T. J. Pedley, “Mapping of Instabilities during Flow through Collapsed Tubes of Differing Length,” Journal of Fluids and Structures, Vol. 4, No. 2, 1990, pp. 125-154. doi:10.1016/0889-9746(90)90058-D
- T. W. Secomb, “Flow in a Channel with Pulsating Wall,” Journal of Fluid Mechanics, Vol. 88, No. 2, 1978, pp. 273-287. doi:10.1017/S0022112078002104
- M. Van Dyke, “Mathematical Approach in Hydrodynamics,” SIAM, Philadelphia, 1997.
- N. M. Bujurke and N. P. Pai, “Computer Extended Series Solution for Flow between Squeezing Plates,” Fluid Dynamics Research, Vol. 16, No. 2-3, 1995, pp. 167-183. doi:10.1016/0169-5983(94)00058-8
- F. M. Skalak and C. Y. Wang, “On the Unsteady Squeezing of a Viscous Fluid from a Tube,” Journal of the Australian Mathematical Society, Vol. 21, 1979, pp. 65-74.
- M. Van Dyke, “Analysis and Improvement of Perturbation Series,” Mathematics & Physical Sciences, Vol. 27, No. 4, 1974, pp. 423-456. doi:10.1093/qjmam/27.4.423
- C. M. Bender and S. A. Orszag, “Advanced Mathematical Methods for Scientists and Engineers,” 3rd International Edition, Springer, New York, 1987.
Appendix
Pade’ Approximants
The basic idea of Pade’ summation is to replace a power series

by a sequence of rational functions of the form

where we choose 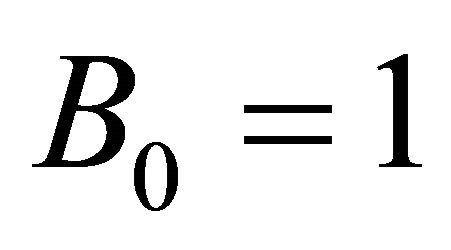 without loss of generality. We determine the remaining (M + N + 1) coefficients
without loss of generality. We determine the remaining (M + N + 1) coefficients 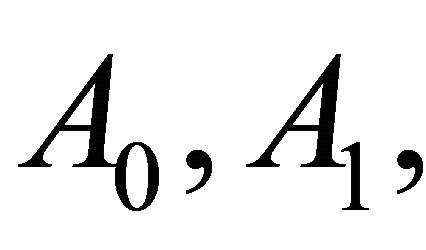
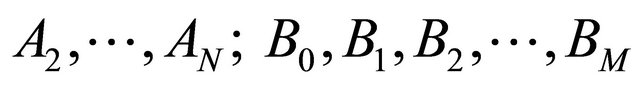 so that the first (M + N + 1) terms in the Taylor’s series expansion of
so that the first (M + N + 1) terms in the Taylor’s series expansion of  match with first (M + N + 1) terms of power series
match with first (M + N + 1) terms of power series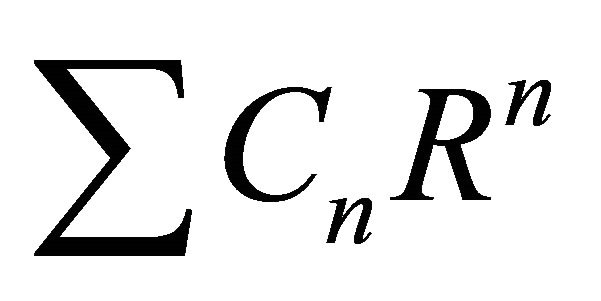 . The resulting rational function
. The resulting rational function 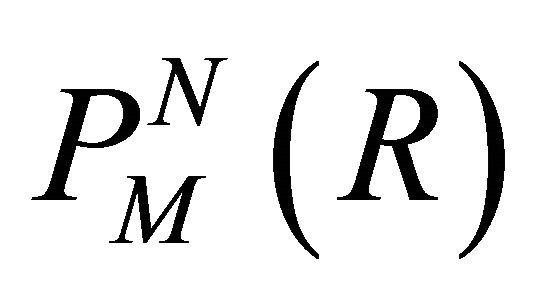 is called a Pade’ approximant. If
is called a Pade’ approximant. If  is a power series representation of the function
is a power series representation of the function , then in favourable cases
, then in favourable cases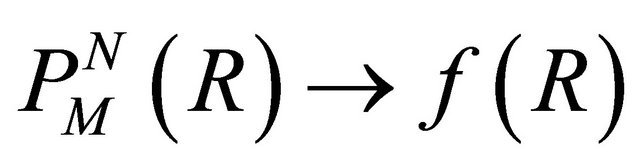 , pointwise as
, pointwise as . There are many methods for the construction of Pade’ approximants. One of the efficient methods for constructing Pade’ approximants is recasting the series into continued fraction form. A continued fraction is an infinite sequence of fractions whose (N + 1)th member has the form
. There are many methods for the construction of Pade’ approximants. One of the efficient methods for constructing Pade’ approximants is recasting the series into continued fraction form. A continued fraction is an infinite sequence of fractions whose (N + 1)th member has the form
 (A)
(A)
The coefficients Dn are determined by expanding the terminated continued fraction 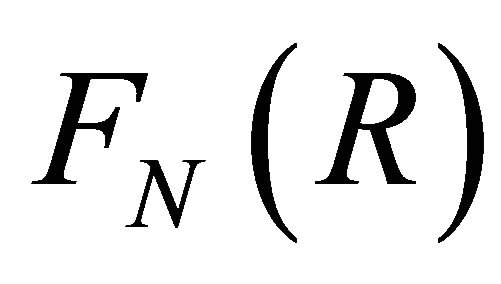 in a Taylor series and comparing with those of the power series to be summed. An efficient procedure for calculating the coefficients Dn’s of the continued fraction (A) may be derived from the algebraic identities (8.4.2a)-(8.4.2c) (Bender and Orszag [7]). Contrary to representations by power series, continued fraction representation may converge in regions that contain isolated singularities of the function to be represented, and in many cases convergence is accelerated. Based on these Dn’s we get terminated continued fractions of various orders from the algorithms (8.4.7), (8.4.8a) and (8.4.8b) (Bender and Orszag [7]).
in a Taylor series and comparing with those of the power series to be summed. An efficient procedure for calculating the coefficients Dn’s of the continued fraction (A) may be derived from the algebraic identities (8.4.2a)-(8.4.2c) (Bender and Orszag [7]). Contrary to representations by power series, continued fraction representation may converge in regions that contain isolated singularities of the function to be represented, and in many cases convergence is accelerated. Based on these Dn’s we get terminated continued fractions of various orders from the algorithms (8.4.7), (8.4.8a) and (8.4.8b) (Bender and Orszag [7]).
Pade’ approximants perform an analytic continuation of the series outside its radius of convergence. It is clear that it can approximate poles by zeros of denominator. With branch points it extracts single valued function by inserting branch cuts, which it simulates by lines of alternating poles and zeros.
NOTES
*Corresponding author.

