American Journal of Computational Mathematics
Vol.2 No.2(2012), Article ID:20088,8 pages DOI:10.4236/ajcm.2012.22014
Exponential Dichotomies and Homoclinic Orbits from Heteroclinic Cycles*
Yiyang Medical College Hunan Pro of China, Yiyang, China
Email: cwwlove@sina.com
Received February 13, 2012; revised April 20, 2012; accepted April 28, 2012
Keywords: Exponential Dichotomies; Homoclinic Orbits; Heteroclinic Cycle; Melnikov Function
ABSTRACT
In this paper, we investigate the homoclinic bifurcations from a heteroclinic cycle by using exponential dichotomies. We give a Melnikov—type condition assuring the existence of homoclinic orbits form heteroclinic cycle. We improve some important results.
1. Introduction
We consider the n-dimensional differential equations
 (1.1)
(1.1)
where  is a small parameter,
is a small parameter,  is a parameter. In studying the global bifurcation, we usuaally assume unperturbed differential equations
is a parameter. In studying the global bifurcation, we usuaally assume unperturbed differential equations
 (1.2)
(1.2)
admits ahyperbolic equilibruim and a homoclinic orbit connecting it. It is the peresistence of homoclinic oribit and heteroclinic that we usually study in global bifurcation, we refer to Wiggins [1], Palmer [2,3], Naudot [4] and Meyer and Sell [5]. But in studying the pulses solutions of some recation-diffusion equations, we often meet the problem of homoclinic bifurcations from the heteroclinic cycles, refer to Kokubu [6], Chow, Deng and Terman [7], Gambaudo [8] and reference therein. Suppose equation (1.2) has two hyperbolic equilibriums 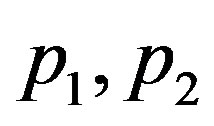 and two homoclinic orbits
and two homoclinic orbits  and two homoclinic orbits
and two homoclinic orbits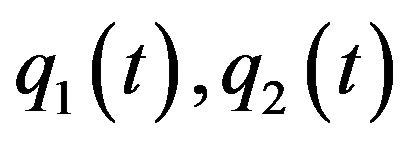 .
.
If
![]() I = 1, 2
I = 1, 2
(where we assume 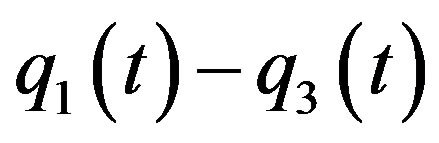
 ) then we say that
) then we say that  is a heteroclinic cycle consisting of
is a heteroclinic cycle consisting of ,
,  ,
, 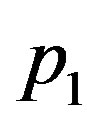 and
and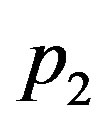 . The study of homoclinic bifurcation from a heteroclinic cycle is very important and interest not only from the point of view of bifurcation theory itself but also from the point of view of application, we refer to Kokubu [6], Chow, Deng and Terman [7]. The main purpose of this paper is to invertigate the homoclinic bifurcation from heteroclinic cycles by making use of exponential dichotomies and Melnikov technique. For convenience, we only discuss the case of heteroclinic cycles with length = 2. Using the theory of exponential dichotomies, Melnikov functions and Slinikov chang of variable, Kokubu [6] investigate the periodic and homoclinic bifurcations from a heteroclinic cycle. In Kokubu [6], he needs to divide the problem into critical and non-critical two cases. Moreover, he needs that the heteroclinic orbits approach the hyperbolic equilibriums along the eignspaces associated with the principal eigenvalues. Chow, Deng and Terman [7] also studied the same problem in the non-critical case by making use of Liapunov-schmidt method and Silnikov’s changes of variable and Poincare map and obtain some analytical results. Chow, Deng and Terman [7] also the conditions as in Kokubu [6]. Melnikov functions were not obtained in Chow, Deng and Terman [7]. Chow, Deng and Terman [9] studied the same problem as this paper, Kokubu [7] did not need to divide the problem into critical and non-critical two cases and unified the two cases and didn’t ndde that the heteroclinic orbits approach the hyperbolic equilibriums along the eigenspaces associated with the principal eigenvalues. The results of Chow, Deng and Terman [9] are weaker than those of Kokubu [6] and Chow, Deng and Terman [7] under weaker assumptions because of the topological approachs.The purpose of this paper is to improve the above results by a analystic method (Lin’s method [10]).We can also unify the critical and non-critical cases and weak the conditions of Kokubu [6], Chow, Deng and Terman [7,9]. Moreover, it is also an interesting to provide an analystic method of studying bifurcations of heteroclinic cycles. Many ideas of this paper come from Lin [10], Meyer and Sell [5], Kokubu [6] and Palmer [2,3]. But it should note that the results of this paper cannot be followed directly from these papers, much technique has been made. Let us finally mention the related results on the bifurcations of heteroclinic cycles. Sandstede [11] investigated the forced symmetry breaking of heteroclinic cycles. Guckenheimer and Holmes [12] discussed the spontaneous symmetry breaking of heteroclinic cycle. Krupa and Melbourne [13] studiecd the stability of heteroclinic cycle. On the other related results on heteroclinic cycles, we refer to the references of the above mentioned papers and good survey of Krupa [14]. The paper is organized as following. In section 2, we give the main result; in section 3, the proof of the main result is given.
. The study of homoclinic bifurcation from a heteroclinic cycle is very important and interest not only from the point of view of bifurcation theory itself but also from the point of view of application, we refer to Kokubu [6], Chow, Deng and Terman [7]. The main purpose of this paper is to invertigate the homoclinic bifurcation from heteroclinic cycles by making use of exponential dichotomies and Melnikov technique. For convenience, we only discuss the case of heteroclinic cycles with length = 2. Using the theory of exponential dichotomies, Melnikov functions and Slinikov chang of variable, Kokubu [6] investigate the periodic and homoclinic bifurcations from a heteroclinic cycle. In Kokubu [6], he needs to divide the problem into critical and non-critical two cases. Moreover, he needs that the heteroclinic orbits approach the hyperbolic equilibriums along the eignspaces associated with the principal eigenvalues. Chow, Deng and Terman [7] also studied the same problem in the non-critical case by making use of Liapunov-schmidt method and Silnikov’s changes of variable and Poincare map and obtain some analytical results. Chow, Deng and Terman [7] also the conditions as in Kokubu [6]. Melnikov functions were not obtained in Chow, Deng and Terman [7]. Chow, Deng and Terman [9] studied the same problem as this paper, Kokubu [7] did not need to divide the problem into critical and non-critical two cases and unified the two cases and didn’t ndde that the heteroclinic orbits approach the hyperbolic equilibriums along the eigenspaces associated with the principal eigenvalues. The results of Chow, Deng and Terman [9] are weaker than those of Kokubu [6] and Chow, Deng and Terman [7] under weaker assumptions because of the topological approachs.The purpose of this paper is to improve the above results by a analystic method (Lin’s method [10]).We can also unify the critical and non-critical cases and weak the conditions of Kokubu [6], Chow, Deng and Terman [7,9]. Moreover, it is also an interesting to provide an analystic method of studying bifurcations of heteroclinic cycles. Many ideas of this paper come from Lin [10], Meyer and Sell [5], Kokubu [6] and Palmer [2,3]. But it should note that the results of this paper cannot be followed directly from these papers, much technique has been made. Let us finally mention the related results on the bifurcations of heteroclinic cycles. Sandstede [11] investigated the forced symmetry breaking of heteroclinic cycles. Guckenheimer and Holmes [12] discussed the spontaneous symmetry breaking of heteroclinic cycle. Krupa and Melbourne [13] studiecd the stability of heteroclinic cycle. On the other related results on heteroclinic cycles, we refer to the references of the above mentioned papers and good survey of Krupa [14]. The paper is organized as following. In section 2, we give the main result; in section 3, the proof of the main result is given.
The main tool used in this paper is theory of exponential dichotomies. We consider the linear differential equations
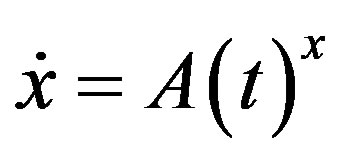 (1.3)
(1.3)
where  A(t) is a n
A(t) is a n  n continuous bounded matrix on R. We say equation (1.3) admits an exponential dichotomy on interval J if ther exist con stants K, α, a projection P and the fundamental matrix X(t) of equation (1.3) satisfying;
n continuous bounded matrix on R. We say equation (1.3) admits an exponential dichotomy on interval J if ther exist con stants K, α, a projection P and the fundamental matrix X(t) of equation (1.3) satisfying;

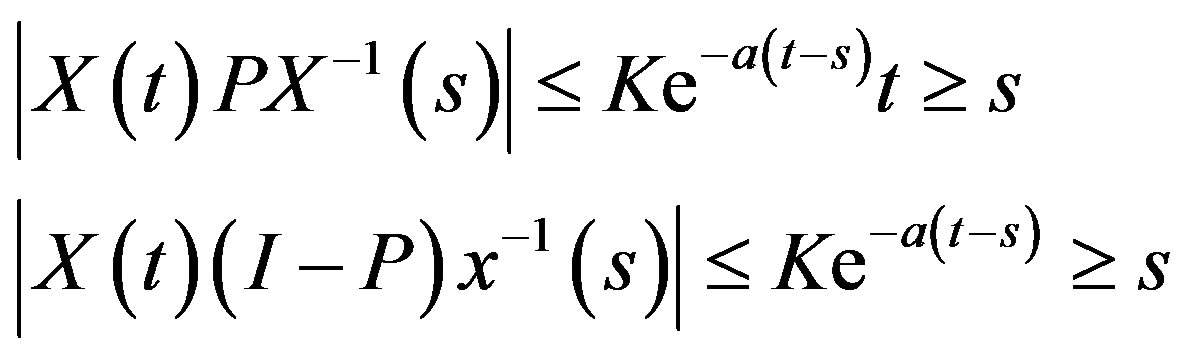
for  On the theory of exponential dichotomies, refer to Coppel [15], Sacker and Sell [16] and Meyer and Sell [17]. On the relations between exponential dichotomies and homoclinic, heteroclinic bifurcations, we refer to Palmer [18] and Meyer and Sell [16].
On the theory of exponential dichotomies, refer to Coppel [15], Sacker and Sell [16] and Meyer and Sell [17]. On the relations between exponential dichotomies and homoclinic, heteroclinic bifurcations, we refer to Palmer [18] and Meyer and Sell [16].
2. Main Result
We consider differential equations
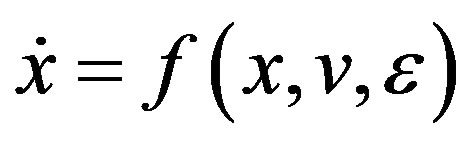 (2.1)
(2.1)
where 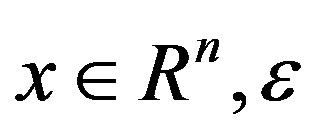 is small parameter,
is small parameter,  is a parameter.
is a parameter.  with respect to
with respect to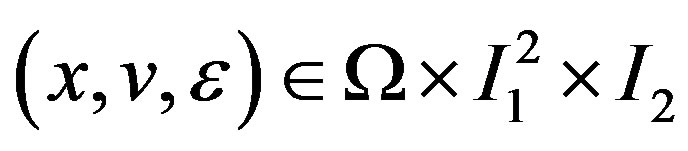 , where
, where  cl\ompact subset,
cl\ompact subset, ![]() a small interval containing zero,
a small interval containing zero,  a small interval.
a small interval.
We assume C1. For 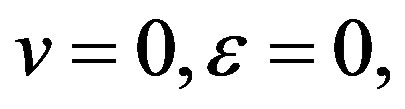 unperturbed equation
unperturbed equation
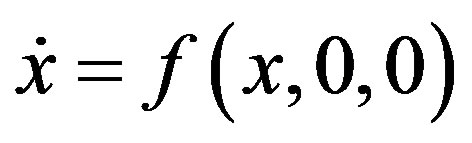 (2.2)
(2.2)
Admits two hyperbolic equilibriums 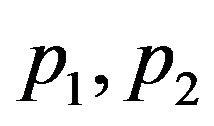 and two heteroclinic orbits
and two heteroclinic orbits  connecting
connecting 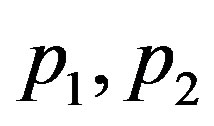 respectively (form a heteroclinic cycle), that is,
respectively (form a heteroclinic cycle), that is,
![]()
![]() .
.
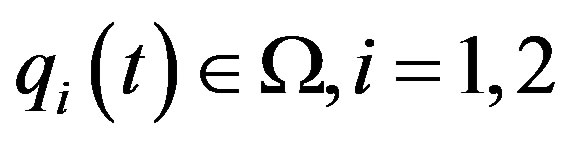 .
.
We denote the heteroclinic cycle by
 .
.
We want to study under what conditions can a homoclinic orbit bifurcate from the heteroclinic cycle ![]() as the second case of Kokubu [6]
as the second case of Kokubu [6]
C2. All real parts of the matrix  are different from zero; and the number of eigenvalues with positive real parts is
are different from zero; and the number of eigenvalues with positive real parts is 
If the conditions C1 and C2 are satisfied then equation
 (2.3)
(2.3)
admit an exponential dichotomy on both 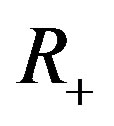 and
and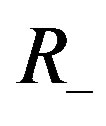 , and the sum of dimensions of stable and unstable subspaces is n. If follows from the roughness of exponential dichotomy that (refer to Zeng [12], Sacker and Sell [16], Coppel [15]) that the variational equations along
, and the sum of dimensions of stable and unstable subspaces is n. If follows from the roughness of exponential dichotomy that (refer to Zeng [12], Sacker and Sell [16], Coppel [15]) that the variational equations along 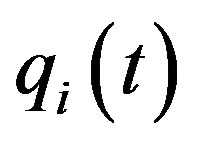
 (2.4)
(2.4)
admit an exponential dichotomy on both 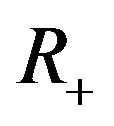 and
and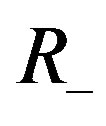 , and the sum of dimensions of the stable and unstable subspaces is
, and the sum of dimensions of the stable and unstable subspaces is  In the follows, because we want to the exponent of
In the follows, because we want to the exponent of  to be greater that 1, without loss of generality, we may assume the constants
to be greater that 1, without loss of generality, we may assume the constants
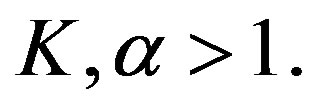 Otherwise, we replace
Otherwise, we replace  by
by 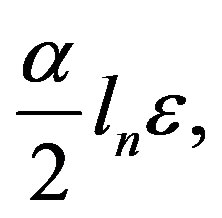 then the exponent of
then the exponent of 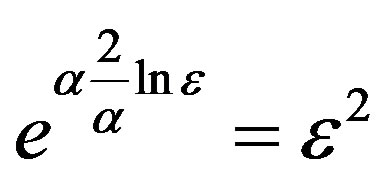 is greater than 1.
is greater than 1.
C3. The variational equations (2.4) admit a unique (up to a scalar multiple) nontrival bounded solution 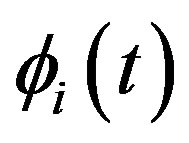 on R.
on R.
Under the conditions C1, C2, C3, we can prove (refer to Zeng [12] that the adjoint equations of equations of (2.3), (2.4)
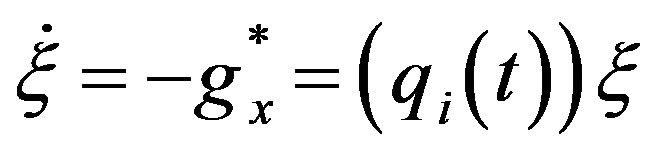
 i = 1, 2 also admit unique (up to a scalar multiple ) nontrival bounded solution
i = 1, 2 also admit unique (up to a scalar multiple ) nontrival bounded solution , respectively, on R, and an exponential dichotomy on both
, respectively, on R, and an exponential dichotomy on both  and
and , respectively. The constants of the exponential dichotomies are also K, α.
, respectively. The constants of the exponential dichotomies are also K, α.
We let
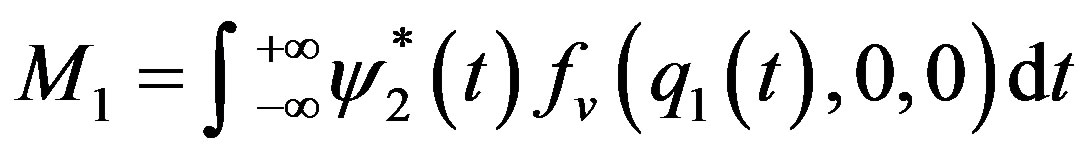 ,
,
 .
.
The main result of this paper is Theorem 1 We assume the conditions C2, C2 and C3 are satisfied, then when  sufficiently small equation (2.1) admits a unique hyperbolic equilibrium
sufficiently small equation (2.1) admits a unique hyperbolic equilibrium 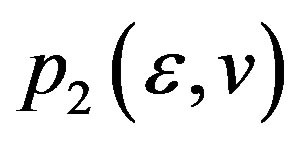 satisfying
satisfying 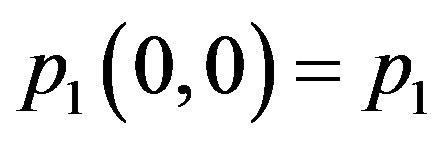 .If the 2 × 2 matrix
.If the 2 × 2 matrix
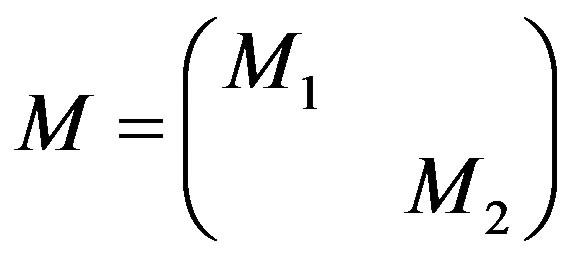
is invertible, the for  sufficiently small there exista a continuous function
sufficiently small there exista a continuous function  satisfying
satisfying
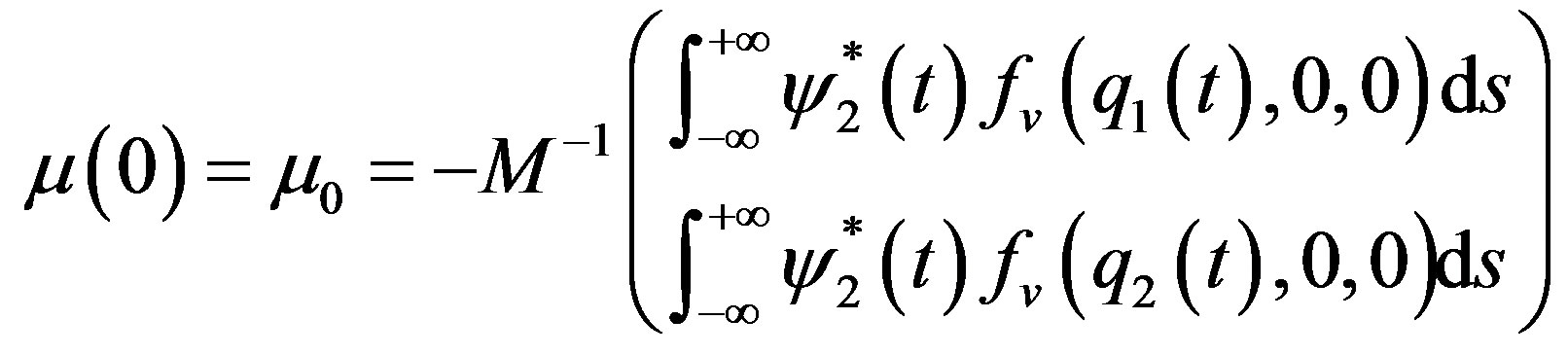
such that the equation
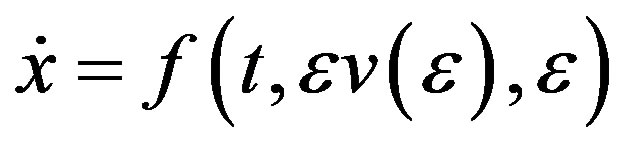 (2.6)
(2.6)
admits a homoclinic orbit connecting 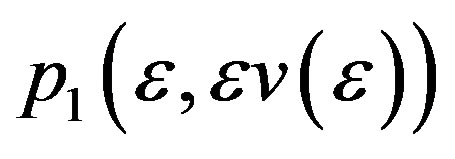 in the neighbourhood of the heteroclinic cycle
in the neighbourhood of the heteroclinic cycle![]() .
.
Remark If the conditions C1, C2 and C3 are satisfied, uing the standard method (refer to Zeng [19]), we can obtain the bifurcative equations of persistence of the two heteroclinic orbits 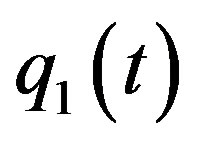 and
and 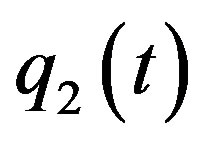
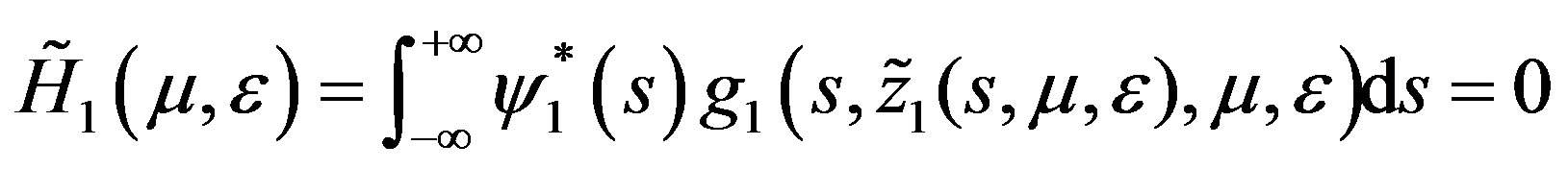 (2.7)
(2.7)
 (2.8)
(2.8)
where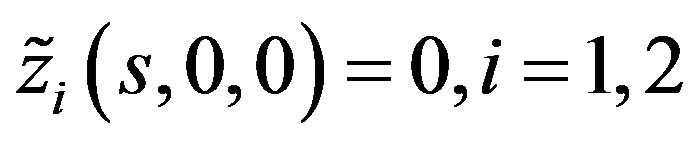 . If the matrix M is invertible then we can easily prove (refer to Zeng [19]) that for
. If the matrix M is invertible then we can easily prove (refer to Zeng [19]) that for 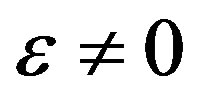 sufficiently small there exits a continuously differentiable function
sufficiently small there exits a continuously differentiable function 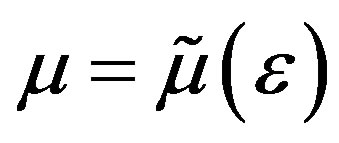 such that
such that
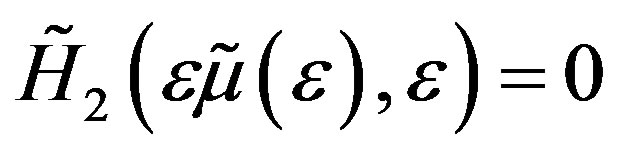
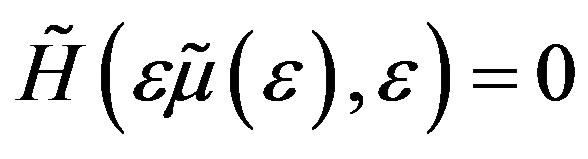
and
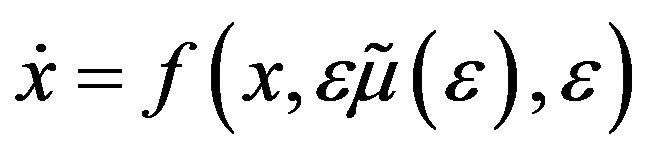 (2.9)
(2.9)
has two hyperbolic equilibriums ,
,  , satisfying
, satisfying  and
and , and two heteroclinic orbits
, and two heteroclinic orbits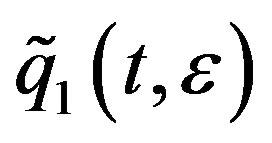 ,
, 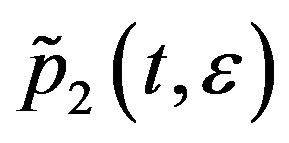 satisfying
satisfying
![]()
![]() ,
,
![]()
![]() .
.
That is, the heteroclinic cycle ![]() persists in the region of parameters
persists in the region of parameters

Fiom Theorem 1 of this paper we see that in the region of parameters
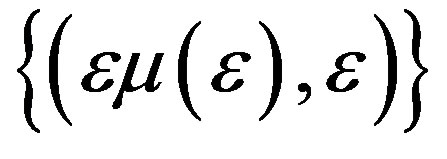
a homoclinic orbit connecting 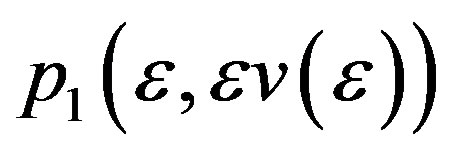 bifurcates from the heteroclinic cycle
bifurcates from the heteroclinic cycle![]() .
.
Kokubu [5] proved that

We can also prove that if the conditions C1, C2 and C3 are satisfied then for  sufficiently small a homoclinic orbit connecting
sufficiently small a homoclinic orbit connecting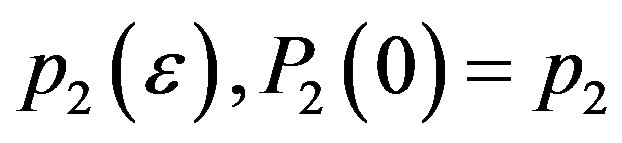 , bifurcates from the heteroclinic cycle
, bifurcates from the heteroclinic cycle![]() , but the region of parameters of bifurcation is different from
, but the region of parameters of bifurcation is different from .
.
3. The Proof of the Main Result
To prove the main result of this paper, we want to find the bounded solutions of equation (2.1)  on
on 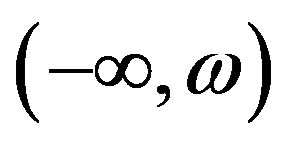 and
and 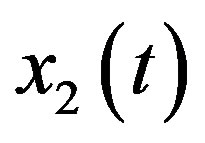 on
on  satisfying
satisfying

We make a change of variables for equation (2.1)
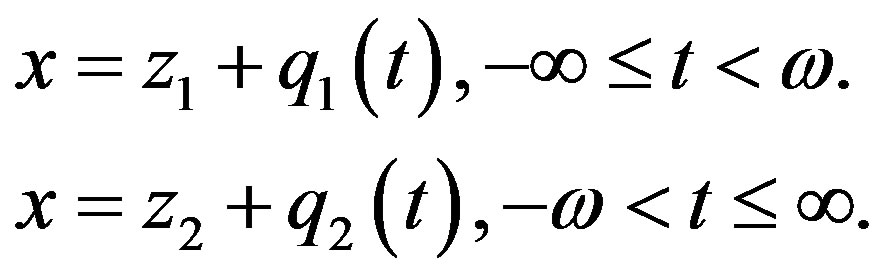
respectively, and obtain the equations
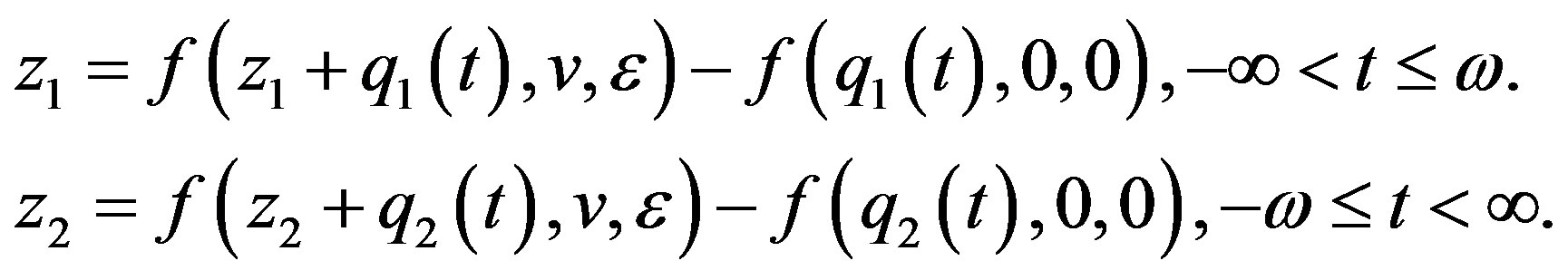
We write the above equations in the following form
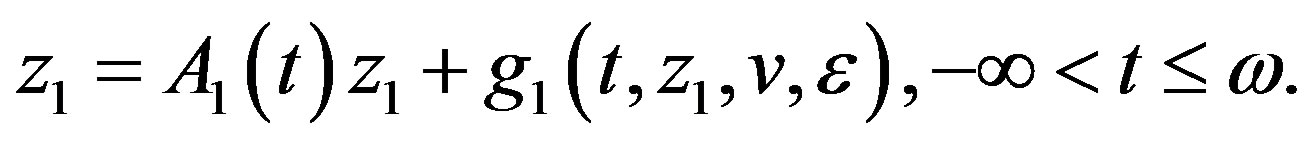 (3.1)
(3.1)
 (3.2)
(3.2)
And the boundary value condition in the following form
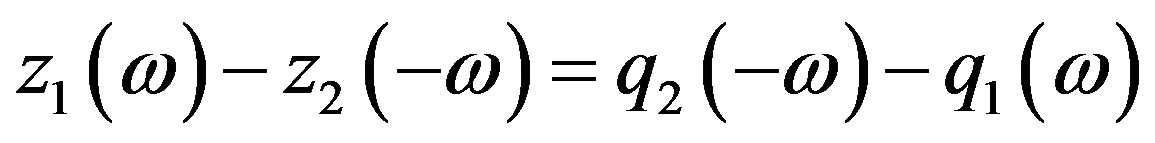 (3.3)
(3.3)
where ![]() is sufficiently large.
is sufficiently large.
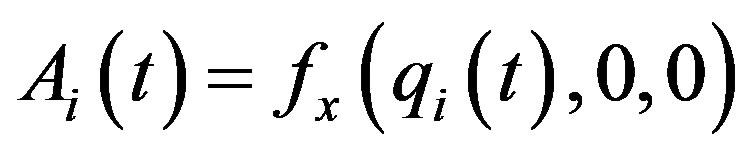 (3.4)
(3.4)
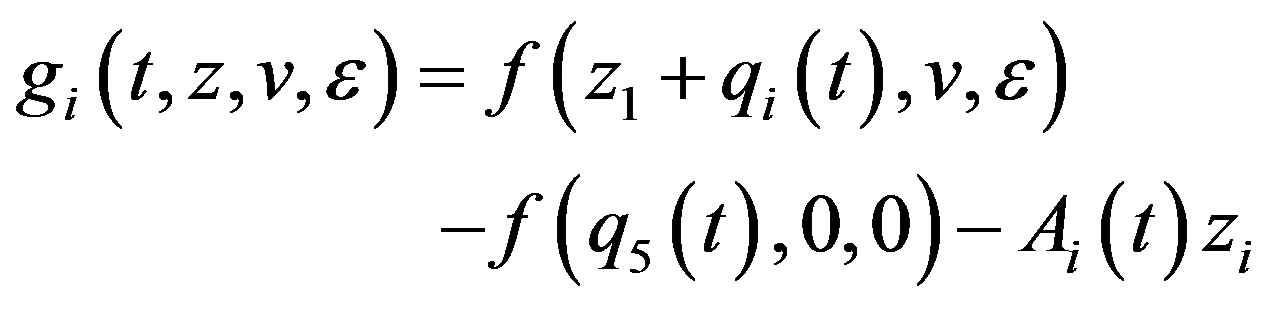
 .
.  satisfying:
satisfying:
 (3.5)
(3.5)
In order to find the bounded solutions of equations (3.1), (3.2) and (3.3), we consider the following boundary value problem
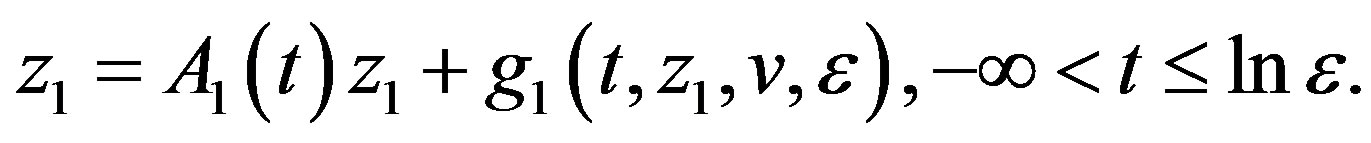 (3.6)
(3.6)
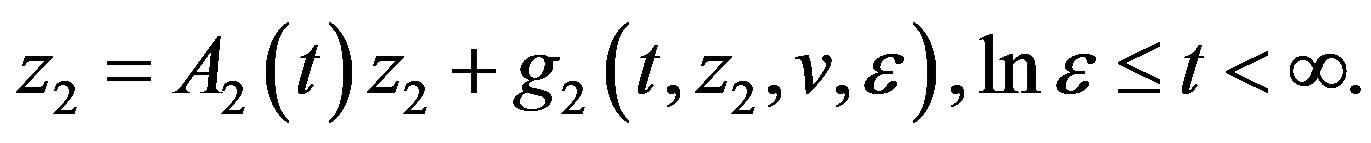 (3.7)
(3.7)
 . (3.8)
. (3.8)
where 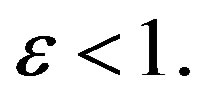 For any
For any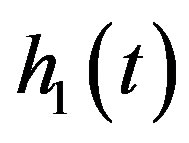 ,
,  , we first consider the following boundary value problems for
, we first consider the following boundary value problems for 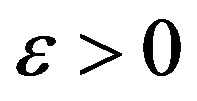
 (3.9)
(3.9)
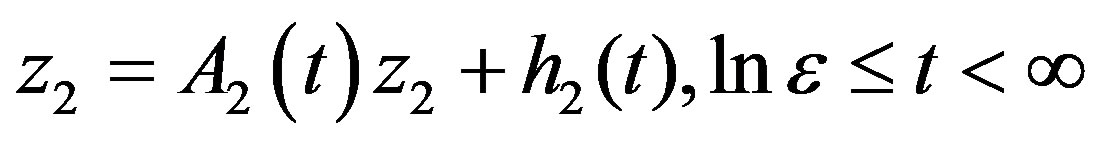 (3.10)
(3.10)
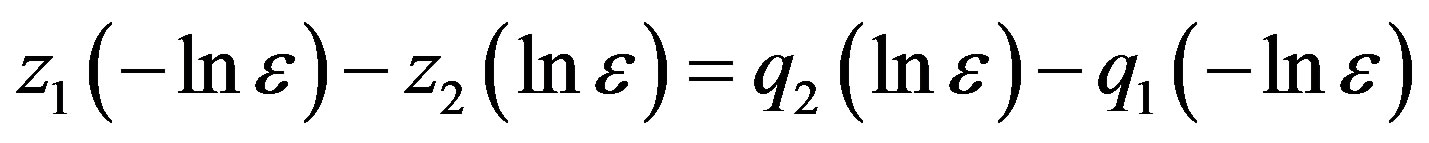 (3.11)
(3.11)
We let  and have the following lemma:
and have the following lemma:
Lemma 1 Assume the conditions C1, C2 and C3 are satisfied.
Then there exists sufficiently small 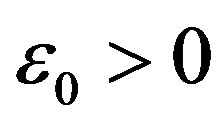 such that for
such that for  equations (3.9), (3.10) and (3.11) admit a unque continuous except at t = 0 bounded solution
equations (3.9), (3.10) and (3.11) admit a unque continuous except at t = 0 bounded solution  satisfying
satisfying 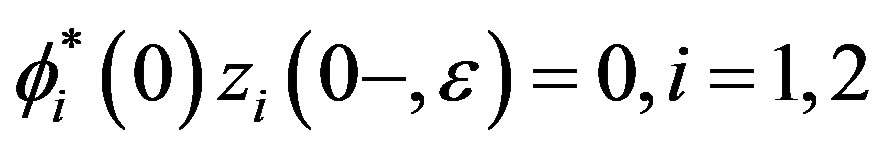 with
with
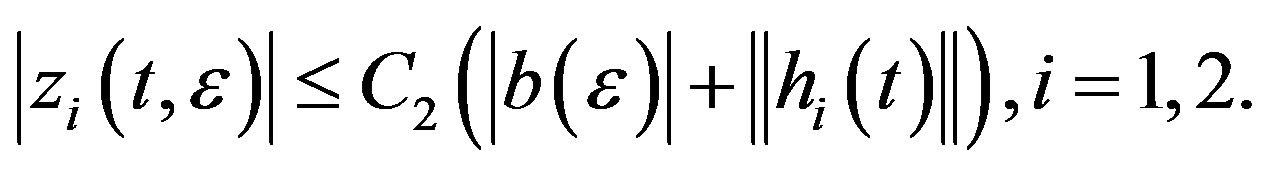 (3.12)
(3.12)
Moreover, 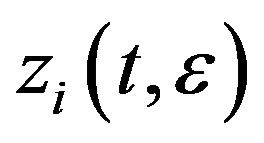 is differentiable in
is differentiable in ![]() and with
and with
 .
.
where 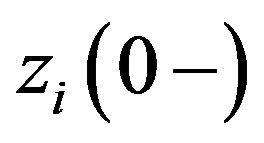 denotes the left limit of function
denotes the left limit of function  at t = 0,
at t = 0, 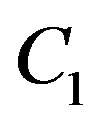 is a constant independent of
is a constant independent of![]() , Moreover, if
, Moreover, if
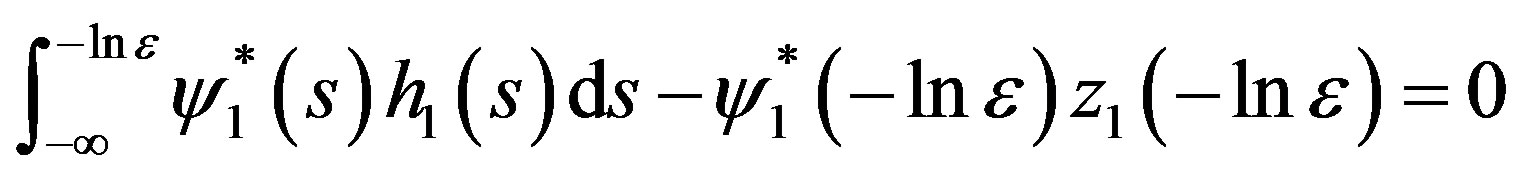 . (3.13)
. (3.13)
 . (3.14)
. (3.14)
then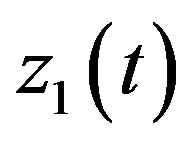 ,
,  are continuous at t = 0.
are continuous at t = 0.
Proof Lemma 2 is mainly due to Lin [10]. For the proof of the first part of existences of the solutions 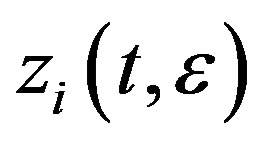 satisfying (3.12), (3.13) and (3.14), we refer to Lin [10] and omit the proof. We now want to prove the second part that
satisfying (3.12), (3.13) and (3.14), we refer to Lin [10] and omit the proof. We now want to prove the second part that 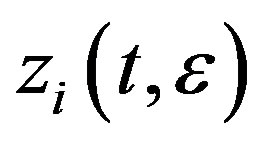 is differentiable in
is differentiable in![]() .We let
.We let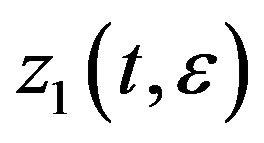 ,
,  be the bounded solutions, which are continous except at t = 0 and satisfy (3.12), (3.13) and (3.14), of equations
be the bounded solutions, which are continous except at t = 0 and satisfy (3.12), (3.13) and (3.14), of equations
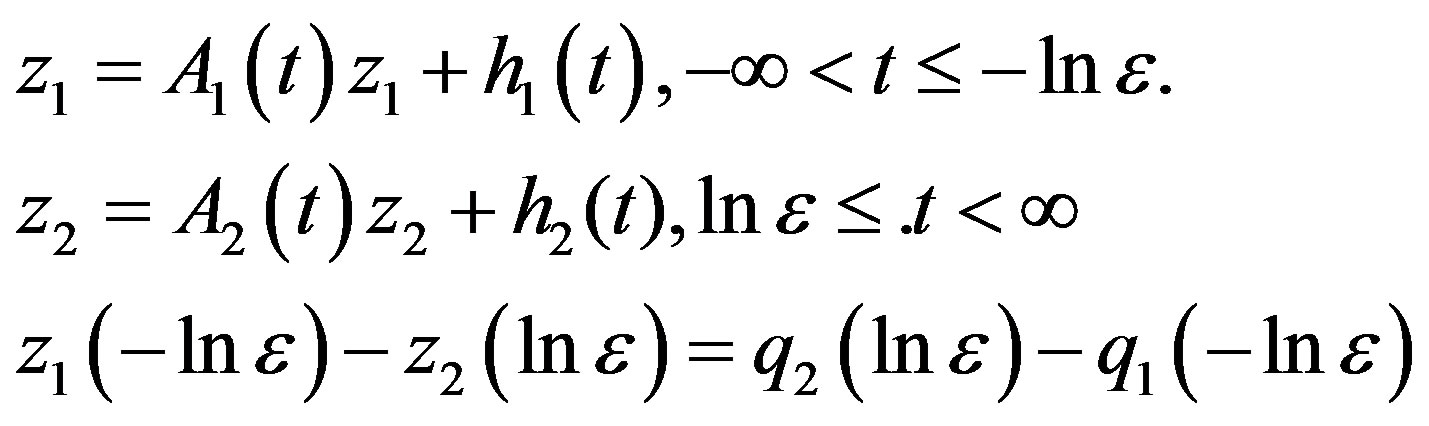
Let ,
, 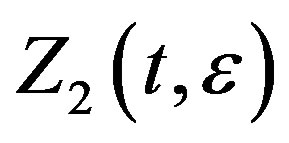 be the bounded solutions of equations
be the bounded solutions of equations

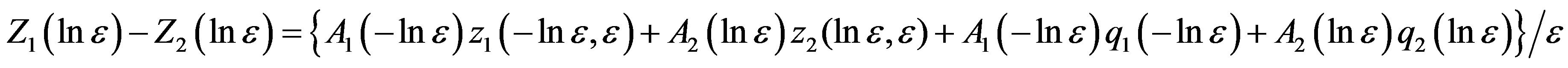
Let
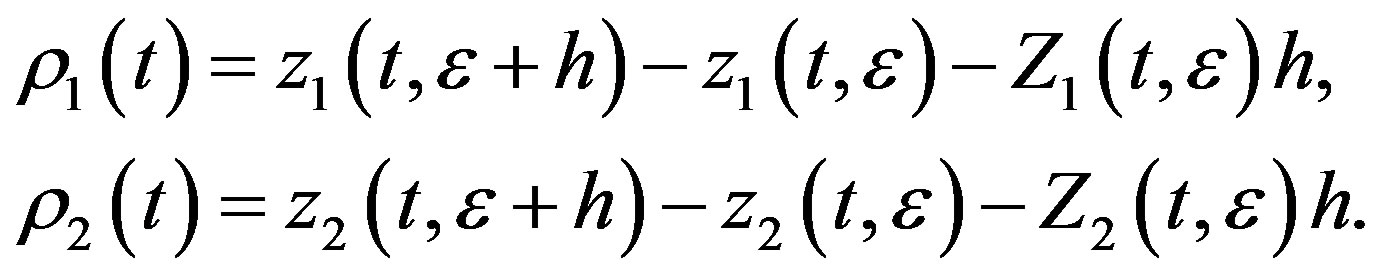
then ,
, 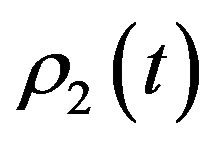 are the solutions of equations
are the solutions of equations
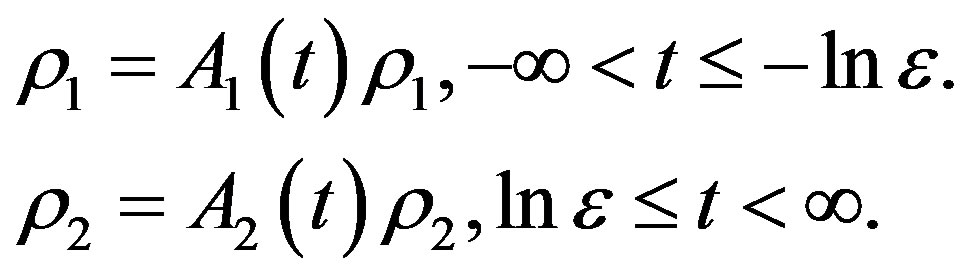
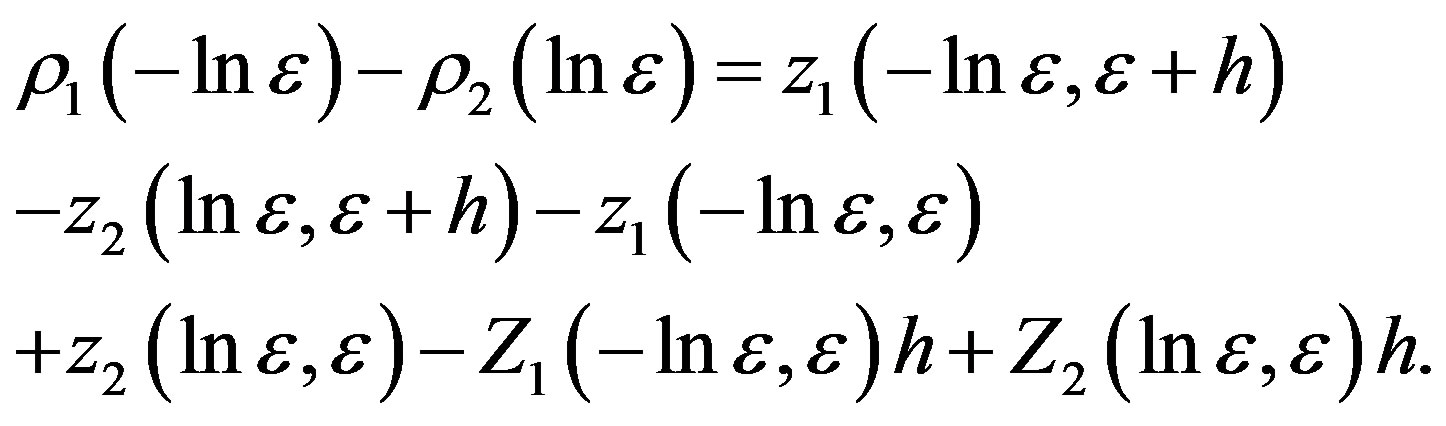
In the same method as follows, we can show that

 .
.
Now we prove the boundness of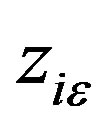 . Let
. Let
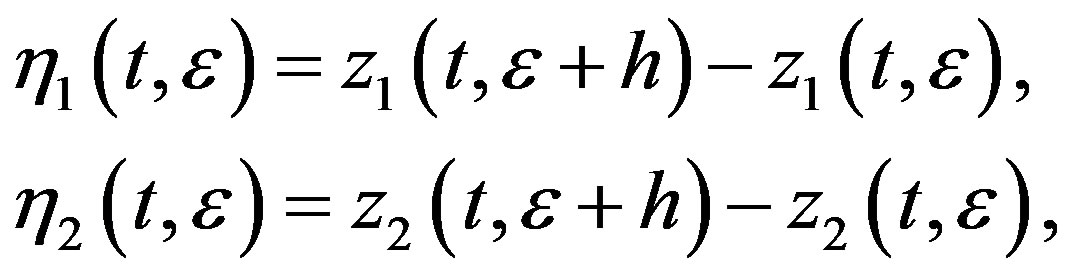
then ,
, 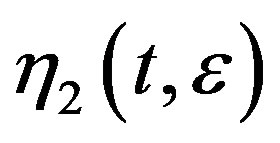 are the solutions of equations
are the solutions of equations
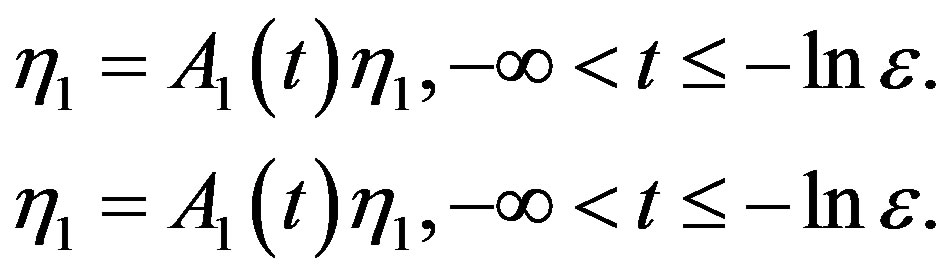

From (3.12) we obtain
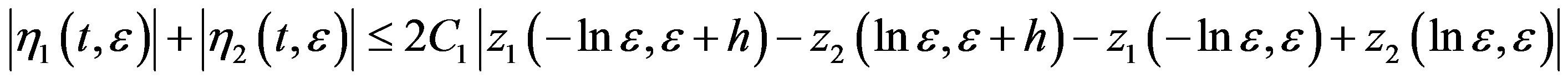
hence there exsits a constant L > 0 such that

This completes the proof of Lemma 2.
Now we consider equations (3.1)-(3.3). We have the following lemama:
Lemma2 Assume conditions C1, C2 and C3 are satisfied. Then there exist sufficiently small  and the constants
and the constants , L > 0 such that for
, L > 0 such that for 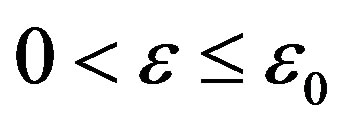 equations (3.1)-(3.3) admit aunque continuous except at t = 0 bounded solution
equations (3.1)-(3.3) admit aunque continuous except at t = 0 bounded solution 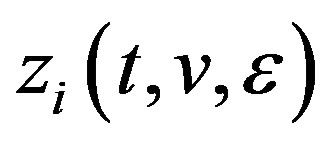 satisfying
satisfying

with

 . (3.15)
. (3.15)
Moreover, if
 (3.16)
(3.16)
 (3.17)
(3.17)
then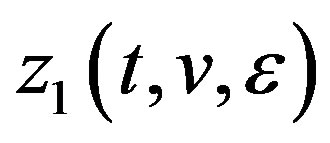 ,
, 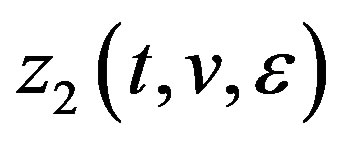 are continuous at t = 0.
are continuous at t = 0.
The proof of Lemma 2 can be proved by contract fixed point theorem and is similar to that of Lin [10].
From Lemma 2 we see that if we have proved that bifurcative equations (3.16) and (3.17) can be can be solved then we find the continuously bounded solutions of equations (3.1), (3.2) and (3.3)
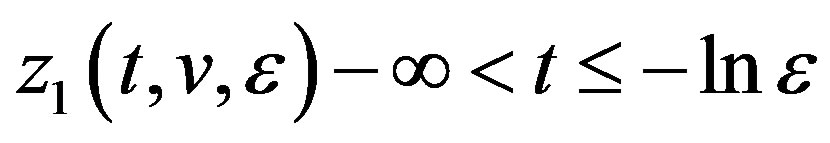
and
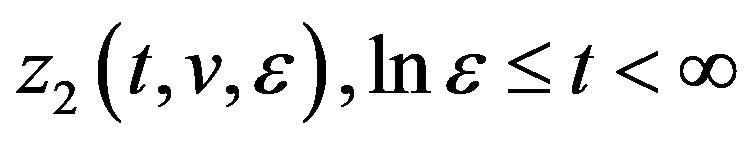 .
.
Now we mainly solve bifurcative equations (3.16) and (3.17). We make a change of variable for equations (3.16) and (3.17) ![]() and obtain the following bifurcative equation
and obtain the following bifurcative equation
 (3.18)
(3.18)
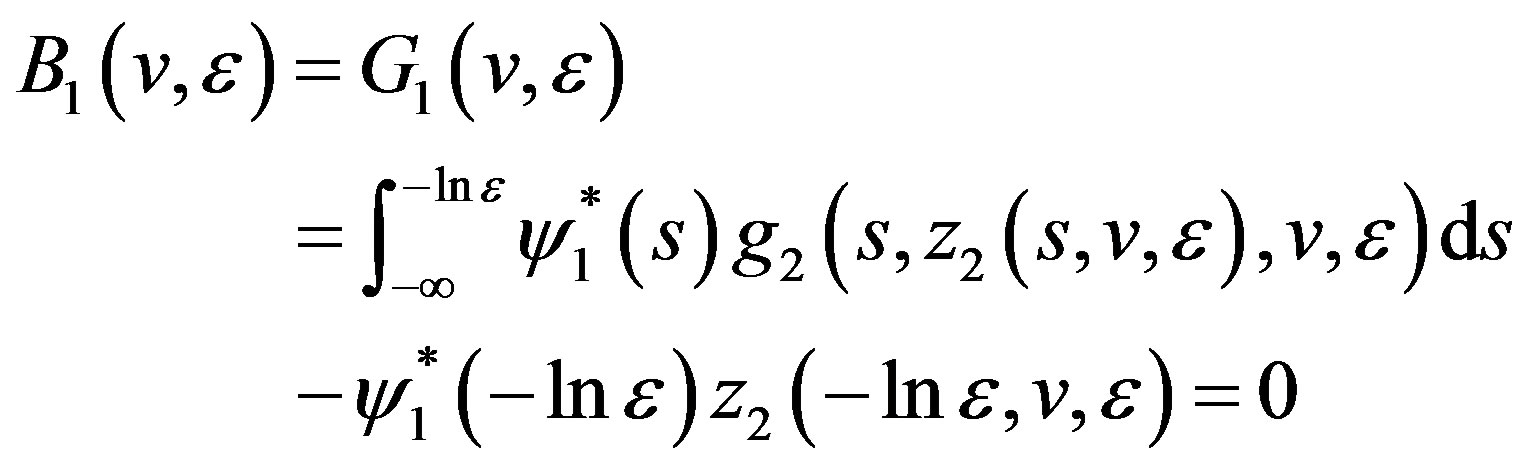 (3.19)
(3.19)
From (3.15) we have
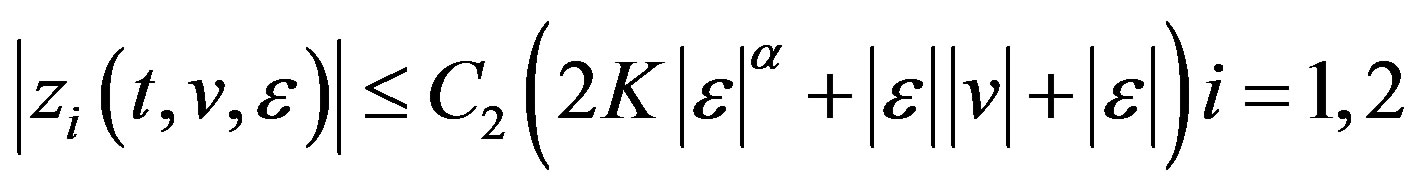 (3.20)
(3.20)
Leting  in the above equation, we obtain
in the above equation, we obtain
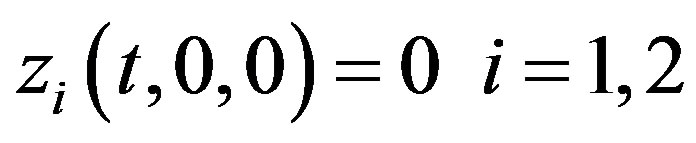 (3.21)
(3.21)
(Remark ACTUALLY,  is defined only for
is defined only for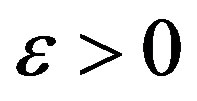 . but due to the existence of its limit, here we define the vaule of the limit to be the value at
. but due to the existence of its limit, here we define the vaule of the limit to be the value at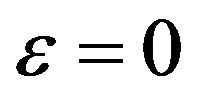 . In the sequel, we make the same definition.)
. In the sequel, we make the same definition.)
From the property of 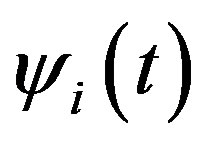 we have
we have
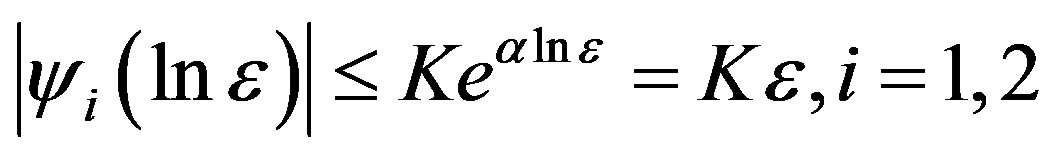
hence
![]() (3.22)
(3.22)
From the representation of (3.18), (3.19), (3.21) and (3.33) we obtain
 (3.23)
(3.23)
In the same way, we can obtain
 (3.24)
(3.24)
For convenience, we define a ![]() matrix
matrix

then we have

We define

Obviously, for 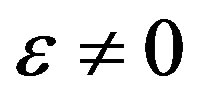 equation
equation
 (3.25)
(3.25)
And equation
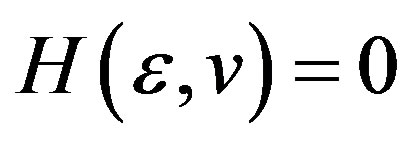 (3.26)
(3.26)
equivalent. Now we want to find the solutions of equation (3.26). We first compute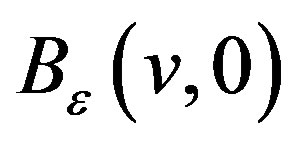 . From (3.18) we have
. From (3.18) we have
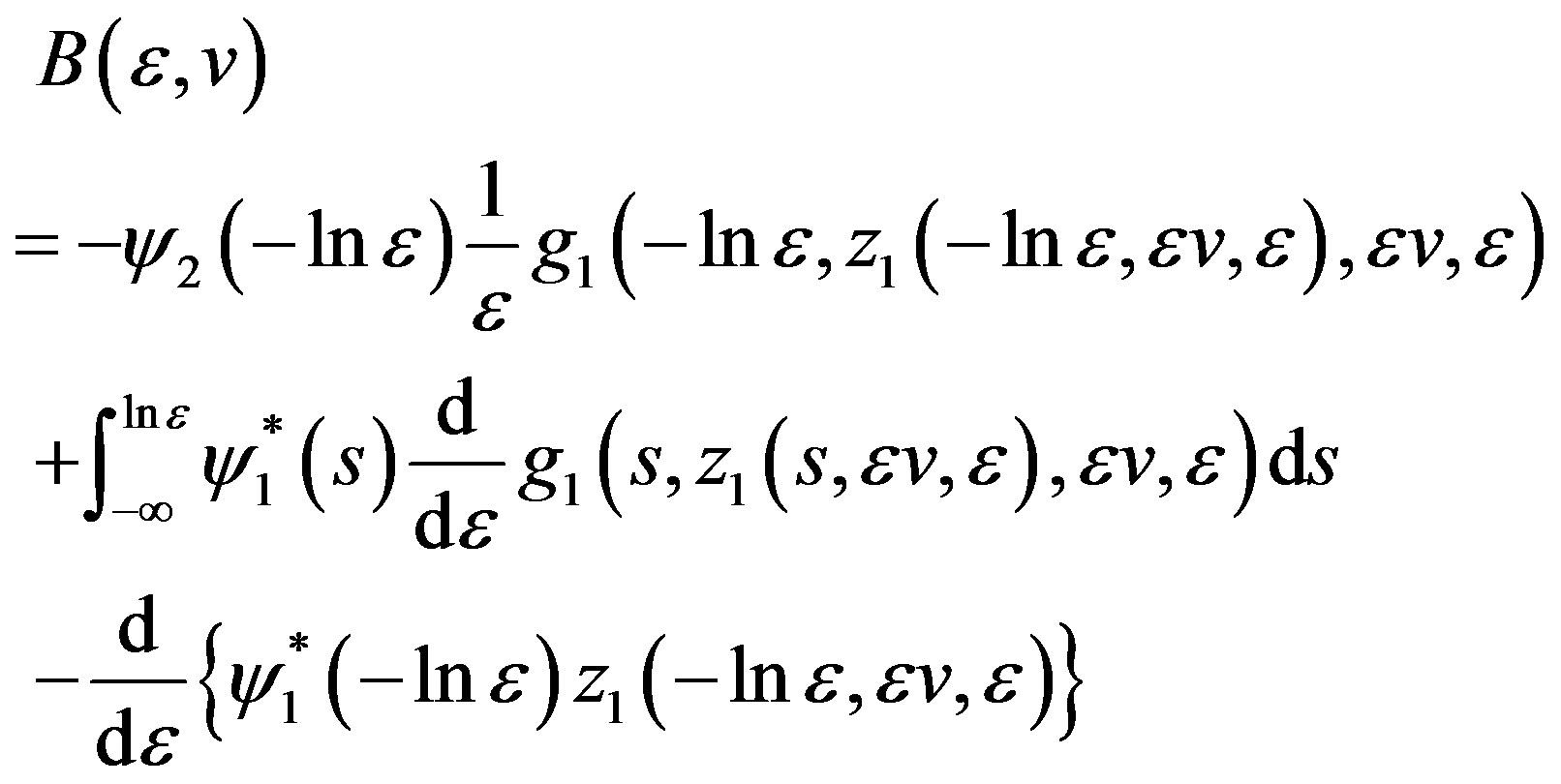 (3.27)
(3.27)
Now we compute (3.27). Since
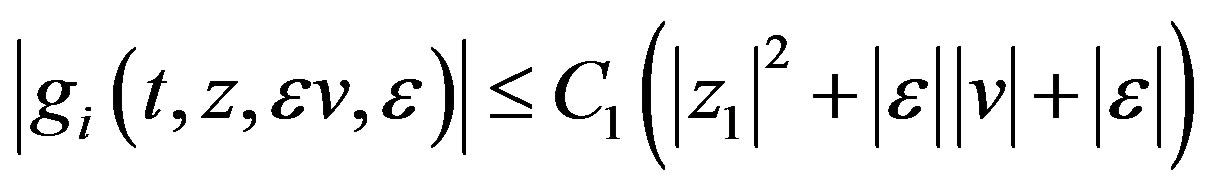
we have
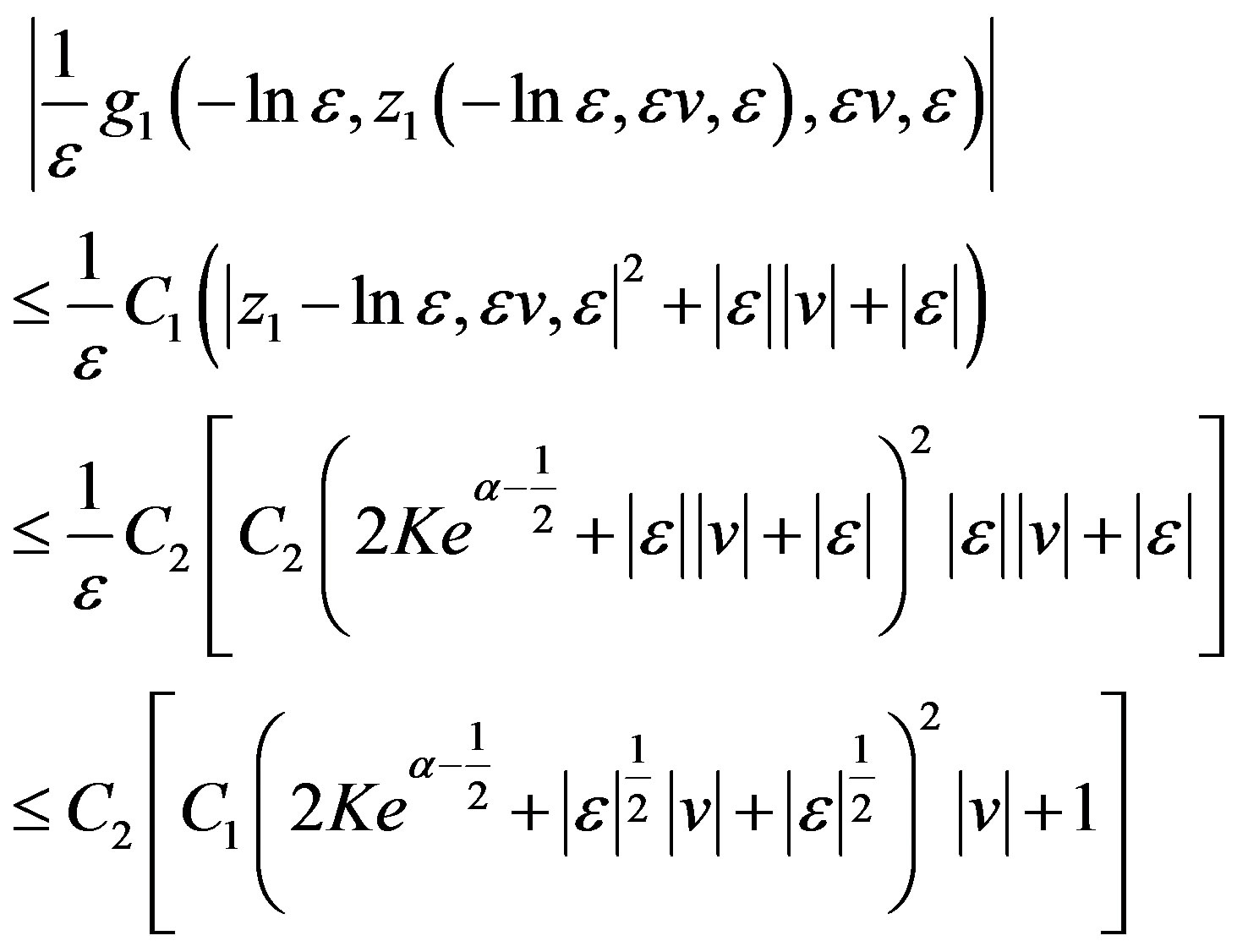
and hence  is bounded for
is bounded for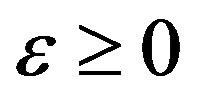 .
.
Since
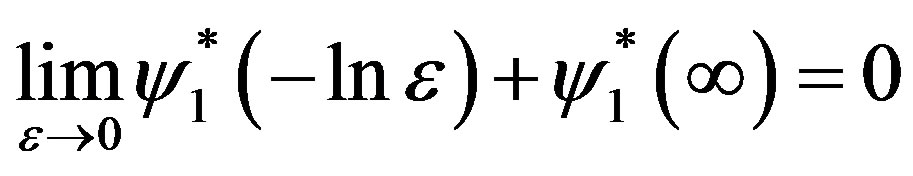 we have
we have
 (3.28)
(3.28)
Noting , we can easily prove that
, we can easily prove that
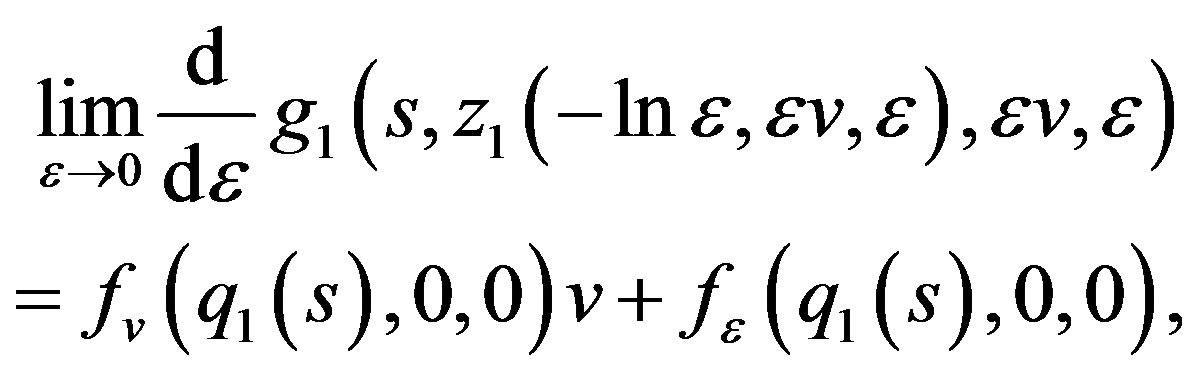
hence
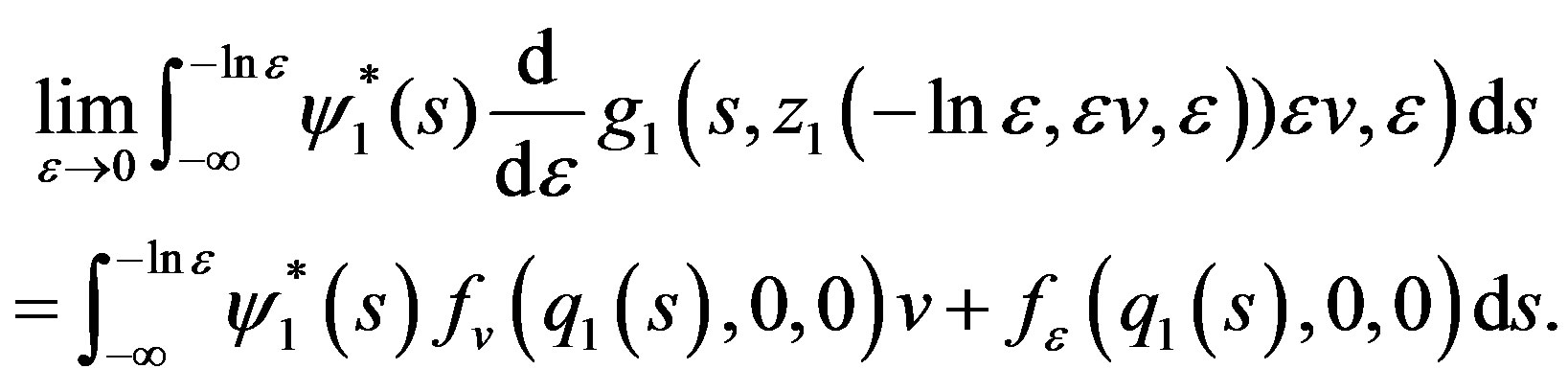 (3.29)
(3.29)
Last, since
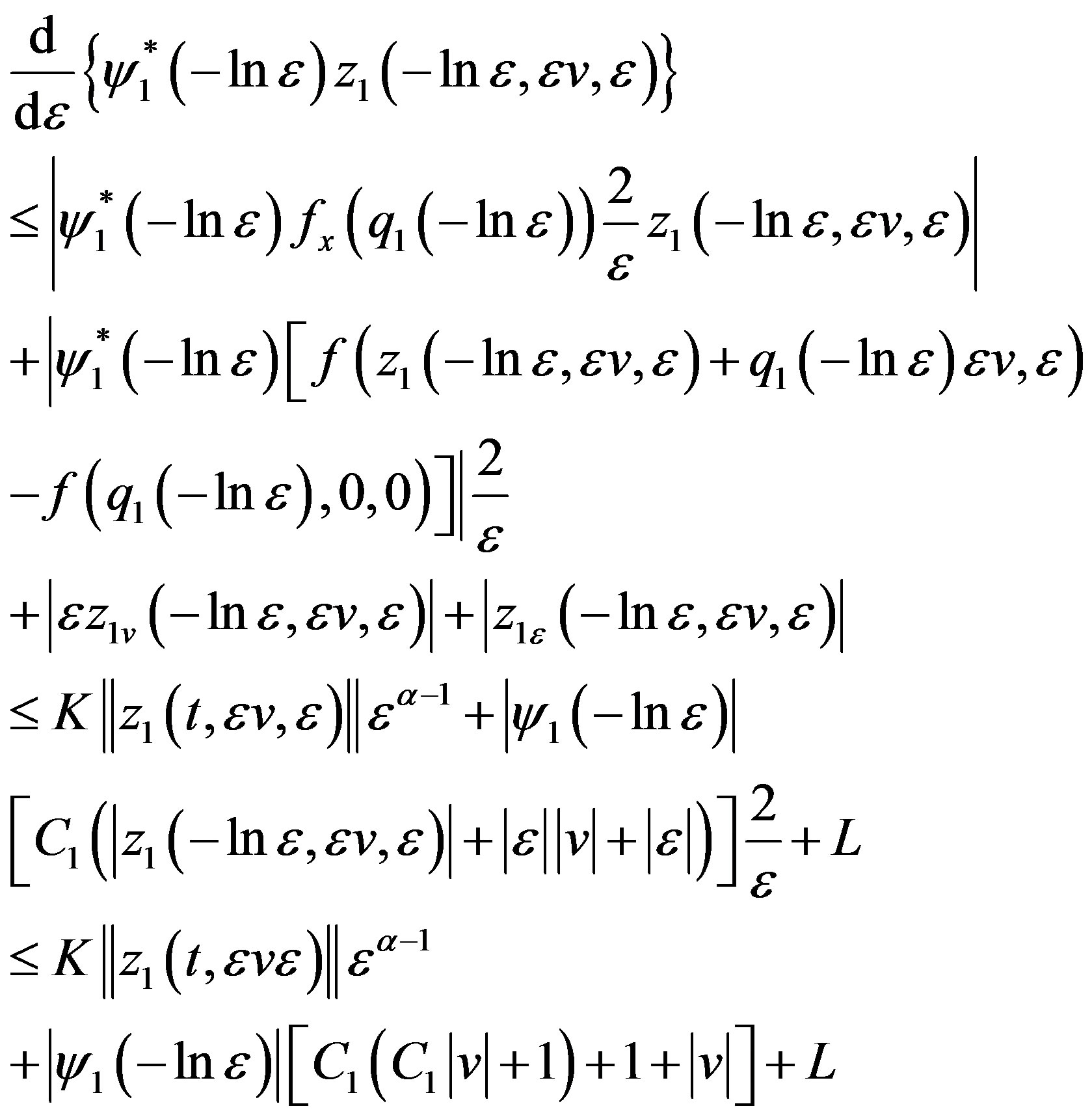 (3.30)
(3.30)
we obtain
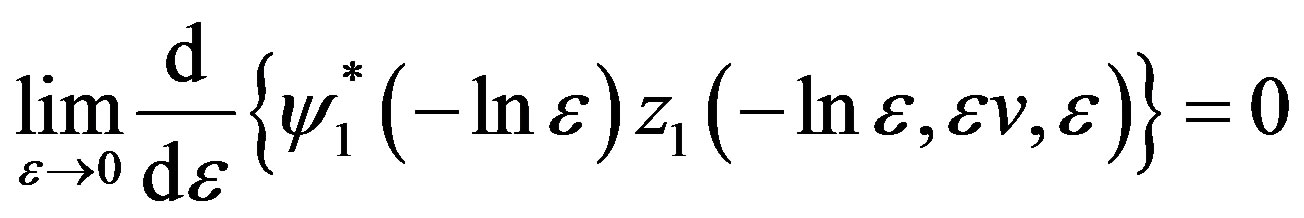 (3.31)
(3.31)
From (3.28), (3.29) and (3.31) we have
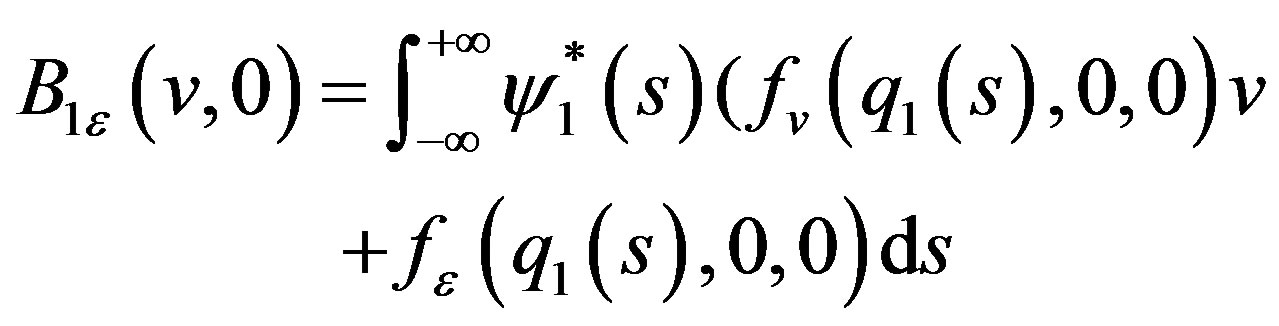 (3.32)
(3.32)
In the same way, we can prove
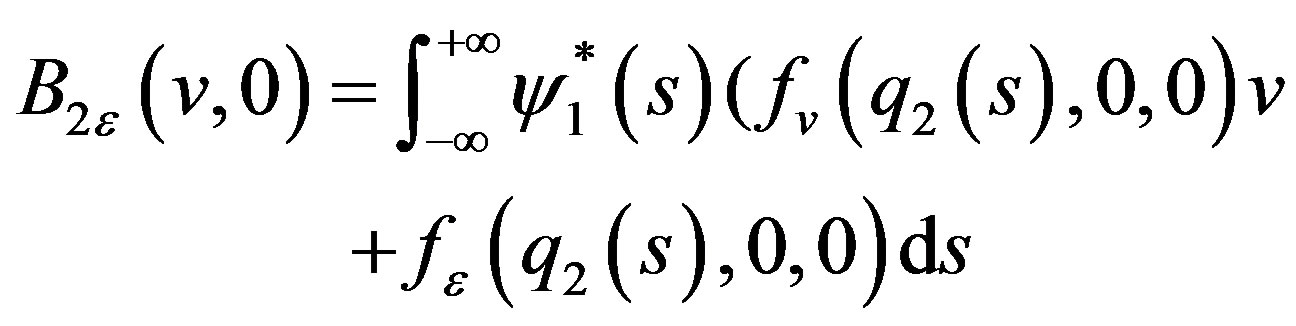 (3.33)
(3.33)
Hence we have
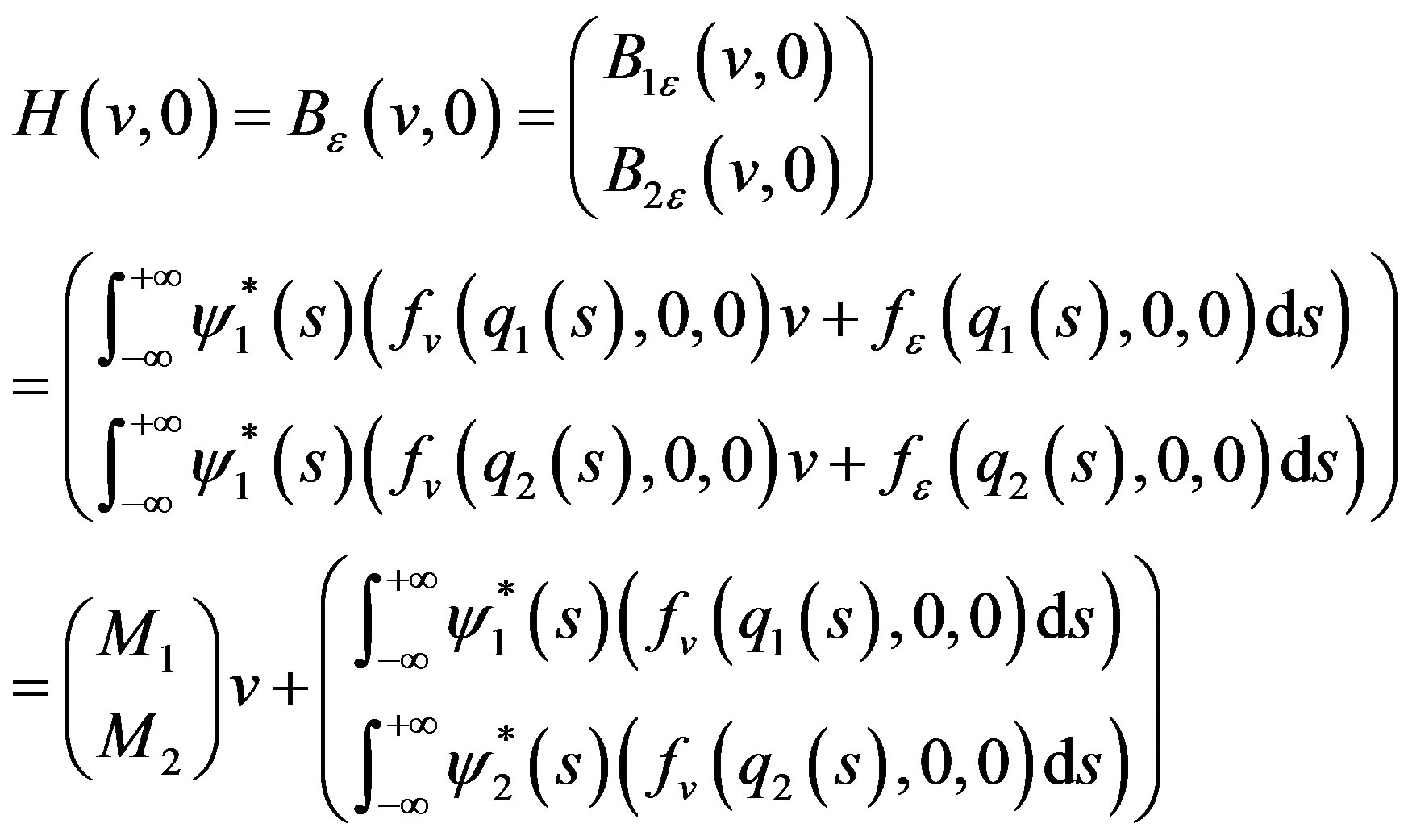
Let

then we have
 (3.35)
(3.35)
From (3.34) we have
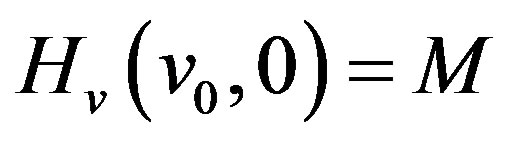 (3.36)
(3.36)
Since the matrix M is invertible, it follows from the implicit function theorem that for 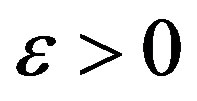 sufficienly small there exists a continuous function
sufficienly small there exists a continuous function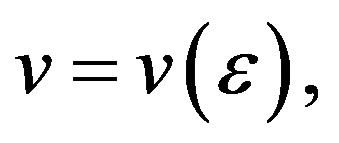
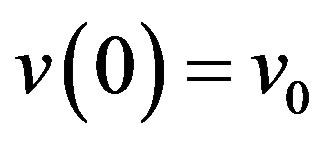 satisfying
satisfying

Hence for 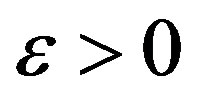 sufficiently small we have
sufficiently small we have
 (3.37)
(3.37)
Hence for  sufficiently small equations (3.6), (3.7) and (3.8)
sufficiently small equations (3.6), (3.7) and (3.8)

So for  sufficiently small the equation
sufficiently small the equation
 . (3.38)
. (3.38)
has two solutions
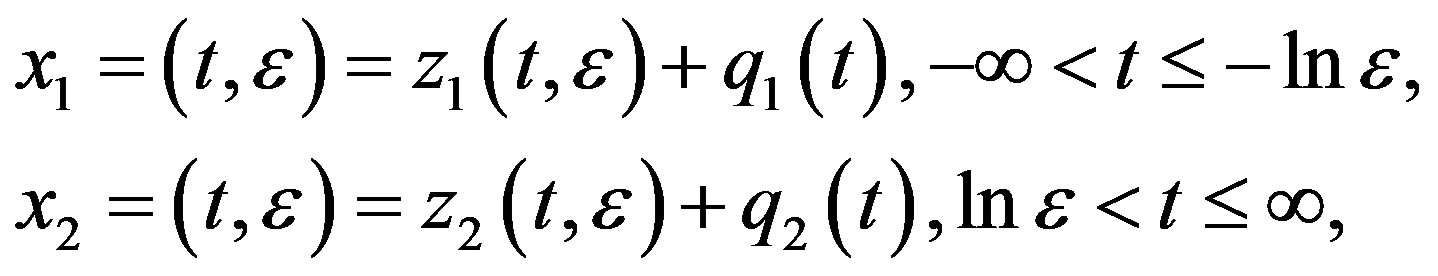
satisfying
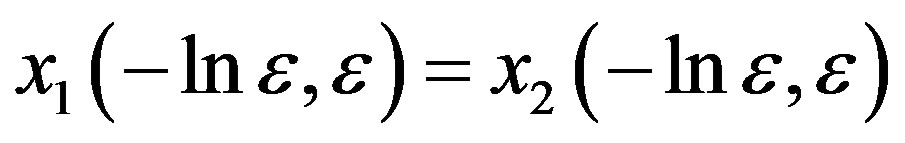
We construct a solution of equation (3.38) by making use of 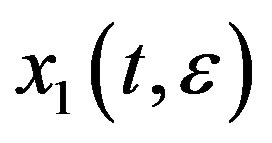 and
and 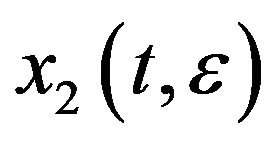

Since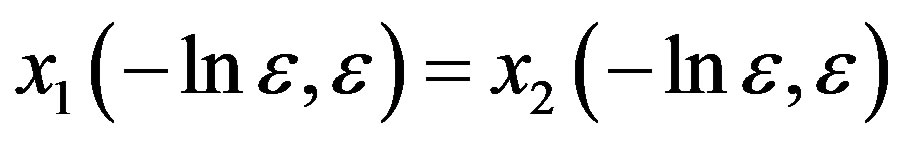 ,
, 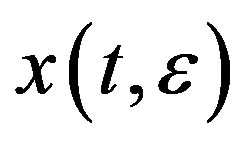 is a continuously bounded solution of equation (3.38).
is a continuously bounded solution of equation (3.38).
Now we show 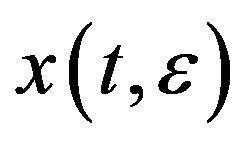 is a homoclinic orbit connecting the equilibrium
is a homoclinic orbit connecting the equilibrium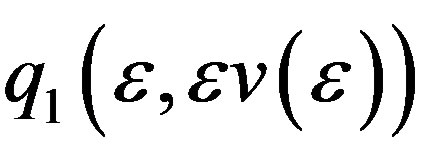 . Since when
. Since when 
 (3.40)
(3.40)
Hence for any , there exist
, there exist 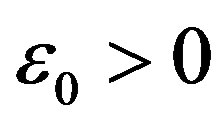 and
and 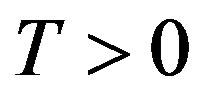 such that when
such that when 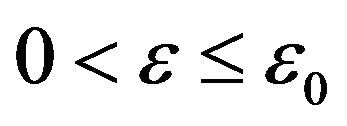 and
and , we have
, we have
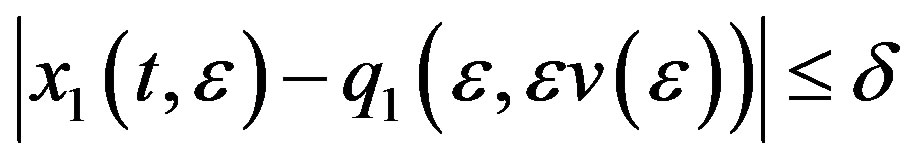
Since  is hyperbolic, we obtain (refer to [9]) for
is hyperbolic, we obtain (refer to [9]) for 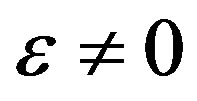 sufficiently small
sufficiently small
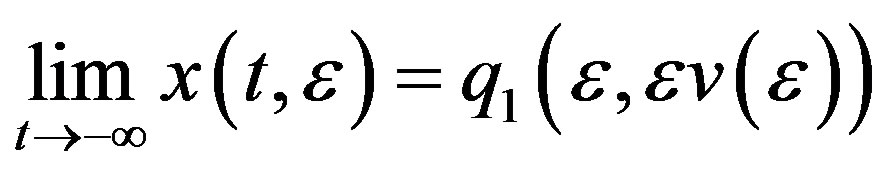
In the same way, we can prove that
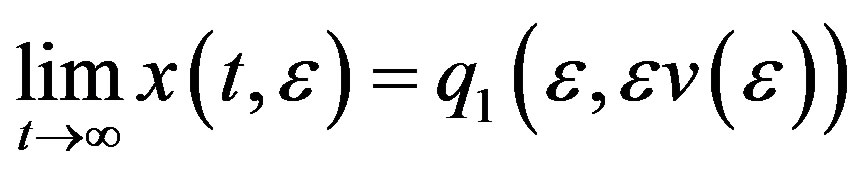
Hence 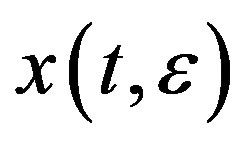 is a homoclinic orbit connecting
is a homoclinic orbit connecting  in the neighbouthood of the heteroclinic cycle
in the neighbouthood of the heteroclinic cycle![]() .
.
Theorem 1 discussed the second case of bifurcations of kokubu [6]. Acutally, we slso investigate the first case of bifurcation as in Figure 2 in the same way and have the following result. We assume B1 for ,
,  , unperturbed equation
, unperturbed equation
 (3.41)
(3.41)
Admits three hyperbolic equilibriums  and two heteroclinic orbits
and two heteroclinic orbits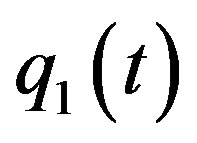 ,
, 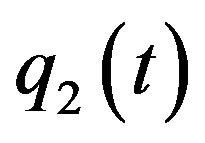 connecting
connecting  to
to ,
,  to
to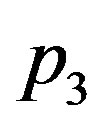 , respectively, that
, respectively, that
![]()
![]()
We denote by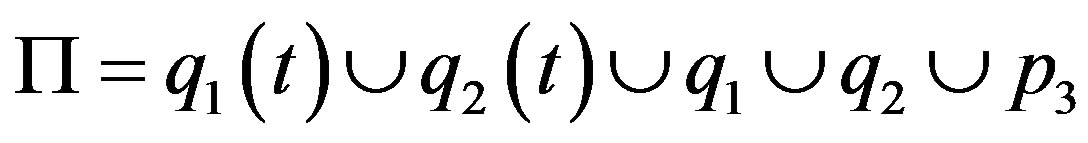 .
.
Theorem 2 We assume the conditions B1, C2 and C3 are satisfied, then when  sufficiently sall equation (1.1) admits two hyperbolic equilibrium
sufficiently sall equation (1.1) admits two hyperbolic equilibrium ,
, 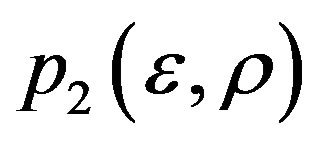 satisfying
satisfying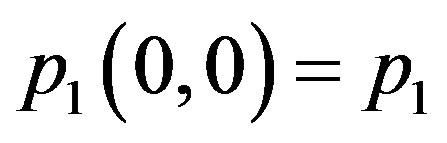 ,
,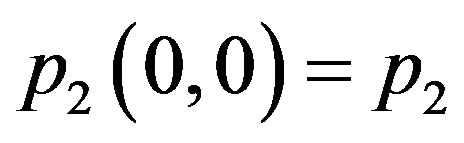 . If the
. If the 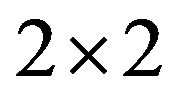 matrix
matrix

Is invertible, then for 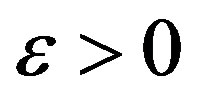 sufficiently small there exists a continuous function
sufficiently small there exists a continuous function 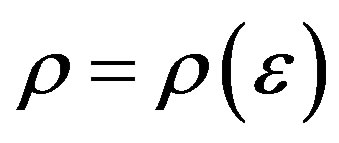 satisfying
satisfying

Such that the equation
 (3.42)
(3.42)
Admits a heteroclinic orbit connecting  to
to 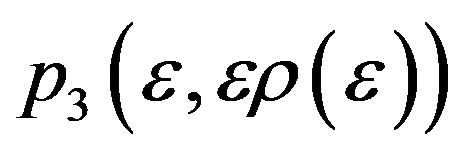 in the neighbourhood of the heteroclinic cycle
in the neighbourhood of the heteroclinic cycle .
.
REFERENCES
- S. Wiggins, “Golbal Bifurcations and Chaos,” SpringerVerlag, New York, 1988.
- K. J. Palmer, “Transversal Heteroclinic Orbits and Cherry’s example of a nonintegrable Hamiltonian system,” Journal of Differential Equations, Vol. 65, No. 3, 1986, pp. 321-360. doi:10.1016/0022-0396(86)90023-9
- K. J. Palmer, “Exponential dichotomies and Transversal Homoclinic Points,” Journal of Differential Equations, Vol. 55, No. 2, 1984, pp. 225-256. doi:10.1016/0022-0396(84)90082-2
- S. Campbell and P. Holmes, “Bifurcation from O(2)sy Mmetric Heterclinic Cycles with Three Interacing Mofes,” Nonlinearity, Vol. 4, 1991, pp. 697-726.
- K. R. Meyer and G. R. Sell, “Melnikov transforms, Bernoulli bundle and almost periodic Perturbations,” Transactions of the American Mathematical Society, Vol. 314, No. 1, 1989, pp. 63-105.
- H. Kokubu, “Homoclinic and heteroclinic bifurcations of vector fields,” Japan Journal of Industrial and Applied Mathematics, Vol. 5, No. 3, 1988, pp. 455-501. doi:10.1007/BF03167912
- S. N. Chow, B. Deng and D. Terman, “the bifurcations of a homoclinic and a Periodic Orbit from Two Heteroclinic Orbits,” SIAM Journal on Mathematical Analysis, Vol. 21, No. 1, 2000, pp. 179-204. doi:10.1137/0521010
- J. M. Gambaudo, P. Glendinning and C. Tresser, “collages de cycles et suites de farey,” Comptes Rendus de l’Académie des Sciences, Vol. 299, 1984, pp. 711-714.
- S. N. Chow, B. Deng and D. Terman, “the bifurcation of a Homoclinic Orbit from Two Heteroclinic Orbits—A Topological Approach,” Applicable Analysis: An International Journal, Vol. 42, No. 1-4, 1991, pp. 1057-1080. doi:10.1080/00036819108840047
- X. B. Lin, “Using Melnikov’s method to solve Silnikov problems,” Proceedings of the Royal Society of Edinburgh: Section A Mathematics, Vol. 116, No. 3-4, 1990, pp. 295-325. doi:10.1017/S0308210500031528
- B. Sandstede and A. Scheel, “Forced Symmetry Breaking of homoclinic cycles,” Nonlinearity, Vol. 8, No. 3, 2009, pp. 333-365. doi:10.1088/0951-7715/8/3/003
- J. Guckenheimer and P. holmes, “Strucarrlly Stable Pulse Heteroclinic Cycles,” Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 103, No. 1, 2008, pp. 189-192. doi:10.1017/S0305004100064732
- M. Krupa and I. Melbourne, “Asymptotic stability of heteroclinic cycles in systems with Symmetry,” Proceedings of the Royal Society of Edinburgh: Section A Mathematics, Vol. 134, No. 6, 2004, pp. 1177-1197. doi:10.1017/S0308210500003693
- M. Krupa, “robust heteroclinic cycles,” Journal of Nonlinear Science, Vol. 7, No. 2, 2011, pp. 129-176. doi:10.1007/BF02677976
- W. A. Coppel, “Dichotomies in Stability Theory, Lecture Notes in Mathematics,” Springer-verlag, New York, 1978.
- R. J. Sacker and G. R. Sell, “A Spectral Theory for Linear Differential Systems,” Journal of Differential Equations, Vol. 27, No. 3, 1978, pp. 320-385. doi:10.1016/0022-0396(78)90057-8
- P. Chossat, M. Krupa, I. Melbourne and A. Scheel, “Transverse bifurcations of homkoclinic cycles,” Physica D: Nonlinear Phenomena, Vol. 100, No. 1-2, 2011, pp. 85- 100. doi:10.1016/S0167-2789(96)00186-8
- V. Naudot, “Hyperbolic dynamice in the unfolding of a degenerate homoclinic orbit,” preprint.
- W. y. Zeng, “Exponential dichotomies and transversal Homoclinic Orbits in Degenerate Cases,” Journal of Dynamics and Differential Equations, Vol. 7, No. 4, 1995, pp. 521-548. doi:10.1007/BF02218723
- G. R. Sell, “Bifurcation of Higher Dimensional Tori,” Archive for Rational Mechanics and Analysi, Vol. 69, No. 3, 1979, pp. 199-230. doi:10.1007/BF00248134
NOTES
*This work is supported by Program for Yiyang Municipal Bureau of Science and Technology of Hunan Pro in China (Ministry YKZ-2011 -30)

