World Journal of Nuclear Science and Technology
Vol.4 No.1(2014), Article ID:42516,7 pages DOI:10.4236/wjnst.2014.41006
Positron Annihilation in Perfect and Defective TiO2 Rutile Crystal with Single Particle Wave Function: Slater Type Orbital and Modified Jastrow Functions
1Faculty of Physics and Engineering Physics, University of Science, Ho Chi Minh City, Vietnam
2Swinburne University of Technology, Melbourne, Australia
Email: thlang@hcmus.edu.vn
Copyright © 2014 Trinh Hoa Lang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Trinh Hoa Lang et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 23, 2013; revised November 27, 2013; accepted December 18, 2013
KEYWORDS
Positron; Annihilation; Jastrow; Lifetime; VQMC; TiO2
ABSTRACT
Positron annihilation in TiO2 rutile crystal is studied by an assumption that a positron binds with valance electrons of a titanium dioxide to form a pseudo TiO2-positron molecule before it annihilates with these electrons. The orbital modification consisting of explicit electron-positron and electron-electron correlation in each electronic orbital is used for the electrons and positron wave functions. By these wave functions, the calculation results of the positron lifetimes in unmitigated and defective TiO2 crystals are about 170 ps, 266 ps and 243 ps, respectively. These results are in good agreement with experimental data of the positron lifetimes in vacancies of TiO2 from 180 ps to 300 ps.
1. Introduction
The structure of material is studied by positron lifetime spectrum, which has many lifetime components depending on a local structure where a positron annihilates with electrons. The problem is how to determine accurately lifetime components of a positron in experiments. It encourages studying deeply the positron annihilation in element-specific structure of materials such as a single atom, a molecule or a unit cell.
In this paper, the study of positron annihilation with valence electrons of a unit structure of a material is assumed that a positron binds with the unit to form a new ground state through these valence electrons before it is destroyed. By this assumption, the orthonormalized Slater type orbital is used to describe electrons and positron wave functions in the irreducible element. Variation Quantum Monte Carlo (VQMC) [1] is then used to find the ground-state wave function for electrons and positron.
When a positron enters the material, it is slowed down to a thermal energy and then bound with atoms in the unit structure before annihilating with valence electrons of the atoms. In this state, the positron wave function is approximated by a hybrid wave function of valence electrons.
The ground state of many-body problem is determined by minimizing the energy of each particle rather than the total energy. The problem of total wave function, Slater determinant representing for exchange effects, is avoided by solving the individual particle equation with the Hamiltonian of exchange potential. One particle energy is derived by one particle equation, which is constructed from the Kohn-Sham method and a single particle wave function. This wave function consists of an atomic wave function and a correlation function. By choosing a trial single wave function, the VQMC method is used to find the ground state of positron-valence electron of a unit element.
In this scenario, the optimized electron and positron distributions in real space of unit structure of material are determined by the minimal energy. From this distributionother quantities will be calculated by Monte Carlo method.
2. Theory
To study the positron annihilation in a unit structure of material, the two-component density-functional theory [2] is used with some modification in single particle wave function and exchange-correlation potential. Beside simple atomic wave function, a single-electron wave function also includes the correlation functions of electronelectron and electron-positron. The set of one-particle Schrodinger equations for electrons and positrons is given by
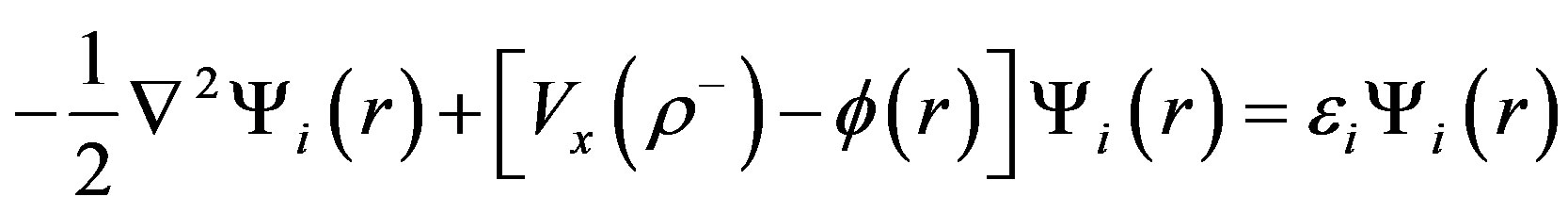 (1)
(1)
 (2)
(2)
with
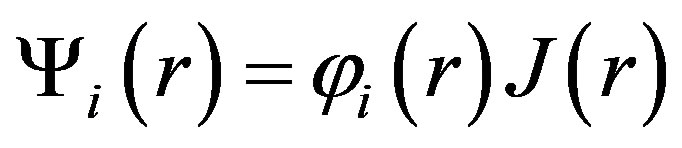 (3)
(3)
where ji is the atomic wave function for a single electron or positron;  is the correlation function of electron-electron or electron-positron. These functions are parameterized functions. The electron and positron densities are calculated by summing over the occupied states (n− and n+ are the number of electrons and positrons respectively).
is the correlation function of electron-electron or electron-positron. These functions are parameterized functions. The electron and positron densities are calculated by summing over the occupied states (n− and n+ are the number of electrons and positrons respectively).
 (4)
(4)
The Slater type wave functions are used for the single electron wave function and the linear combination of them is used for the single positron wave function. The correlation function has the form  and
and 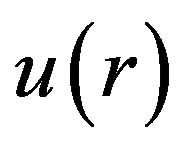 is the Jastrow function. This function is suggested in the new modified Jastrow function which is a combination of long correlation Padé [1] and short correlation Yukawa [3]. The Jastrow function for the electron-electron correlation is given by
is the Jastrow function. This function is suggested in the new modified Jastrow function which is a combination of long correlation Padé [1] and short correlation Yukawa [3]. The Jastrow function for the electron-electron correlation is given by
 (5)
(5)
and for the electron-positron correlation is given by
 (6)
(6)
where be, ae, Ae, Fe, bep, aep, Aep, and Fep are the variation parameters. These parameters depend on the electronic structure of material.
If the exchange-correlation potential is separated into exchange and correlation potentials, then the correlation potential is hidden in the correlation wave function, and the exchange potential for a uniform degenerate electron gas is adapted in the atomic calculation by using local electron density as given by [4]
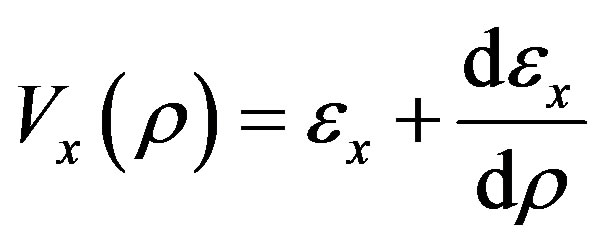 (7)
(7)
where ex is the exchange energy per electron of a uniform electron gas with density r.
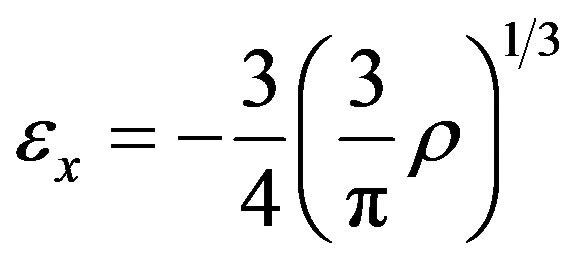 (8)
(8)
Now r is replaced by a local electron density in an atom.
The Equations (1) and (2) are solved with the wave function in Equations (3), (5) and (6) to find the ground state of the unit structure-positron system by VQMC, which minimizes the electron and positron energy to obtain their ground state wave function.
The pair correlation function of electron and positron is built from Monte Carlo simulation in the ground state. The analytical form of pair correlation function is fitted to the Chebyshev polynomial. Then the positron annihilation enhancement is determined by extrapolating the pair correlation function at r = 0, which is the distance between electron and positron.
Positron annihilation rate, which depends on the overlap of electron and positron densities and the enhancement factor, is directly given by the value of the pair-correlation function at the origin via the relation [5,6]
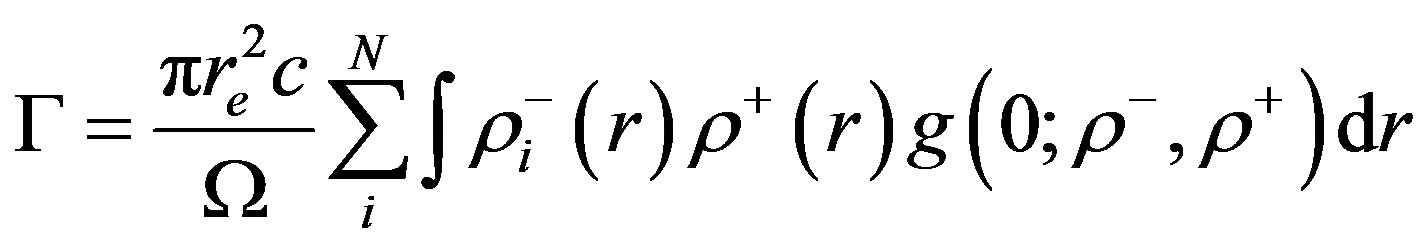 (9)
(9)
where  , the value of the pair-correlation function
, the value of the pair-correlation function 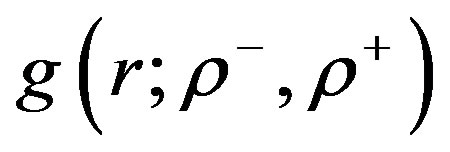 at r = 0 for given electron density, is the enhancement factor. the pair-correlation function is fitted to the Chebyshev polynomial [7] as given by
at r = 0 for given electron density, is the enhancement factor. the pair-correlation function is fitted to the Chebyshev polynomial [7] as given by
 (10)
(10)
where L is the maximum interaction range of the electron and the positron, which is used for determining the electron distribution in the space around the positron.
This model is applied to study the positron annihilation in the unit cell of titanium dioxide of rutile structure consisting of two titaniums and four oxygens as shown in Figure 1. The single-particle wave function in TiO2 is constructed by the Linear Combination of Atomic Orbitals (LCAO) approximation [8] from an atomic wave function of oxygen and titanium.
The single-particle wave functions for the valance electrons of titanium and oxygen atoms in 3d, 4s and 2p shells are obtained from the Slater Type Orbital [9] and

Figure 1. The schematic of the titanium dioxide-positron system and the configuration of the titanium dioxide in a unit cell of rutile crystal structure. The big spheres are titaniums and the smaller spheres are oxygens.
are constructed by the LCAO approximation as shown.
 (11)
(11)
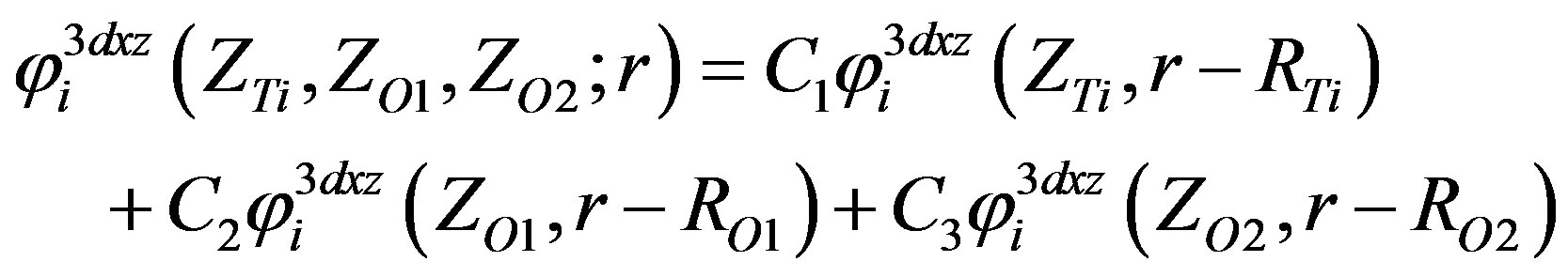 (12)
(12)
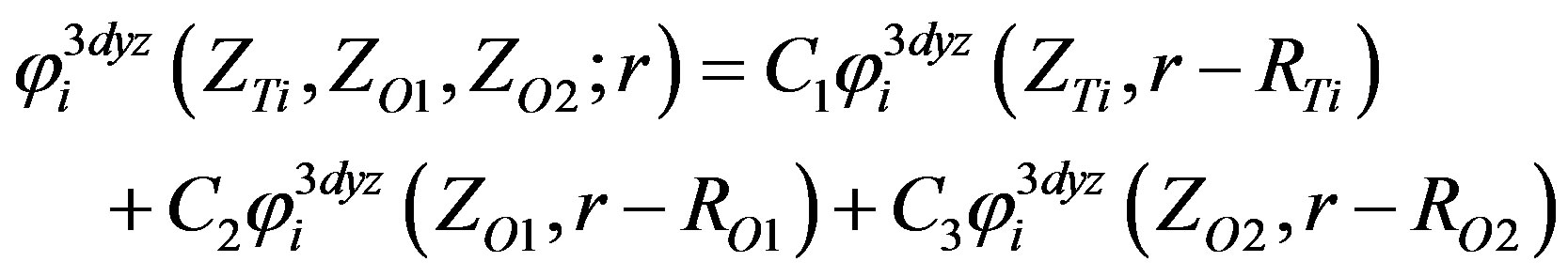 (13)
(13)
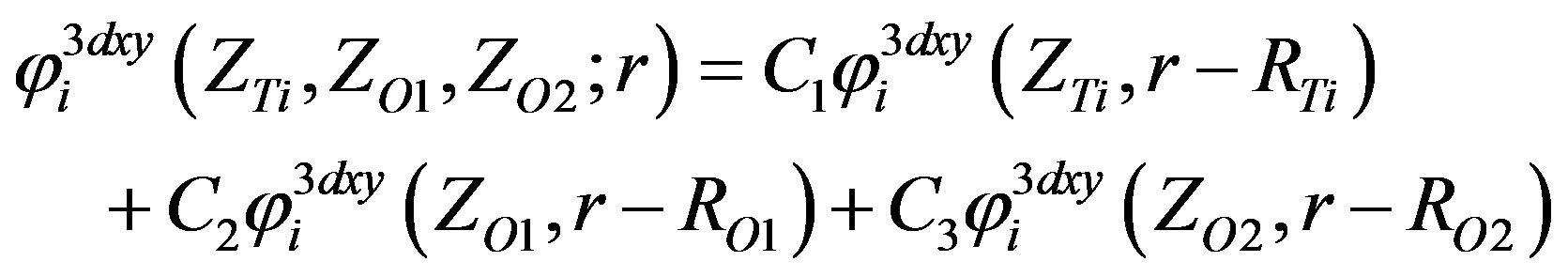 (14)
(14)
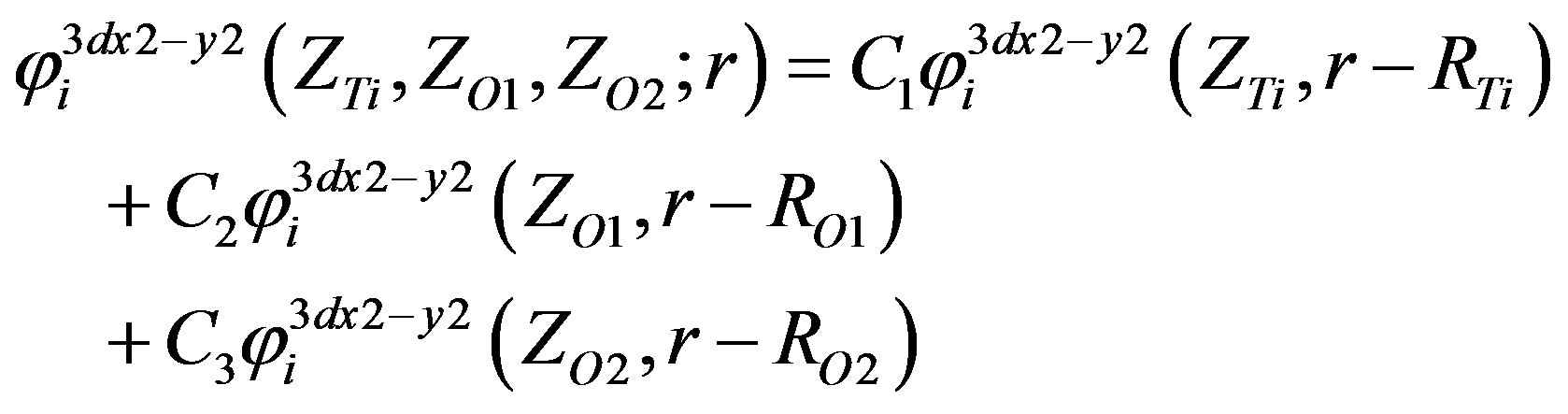 (15)
(15)
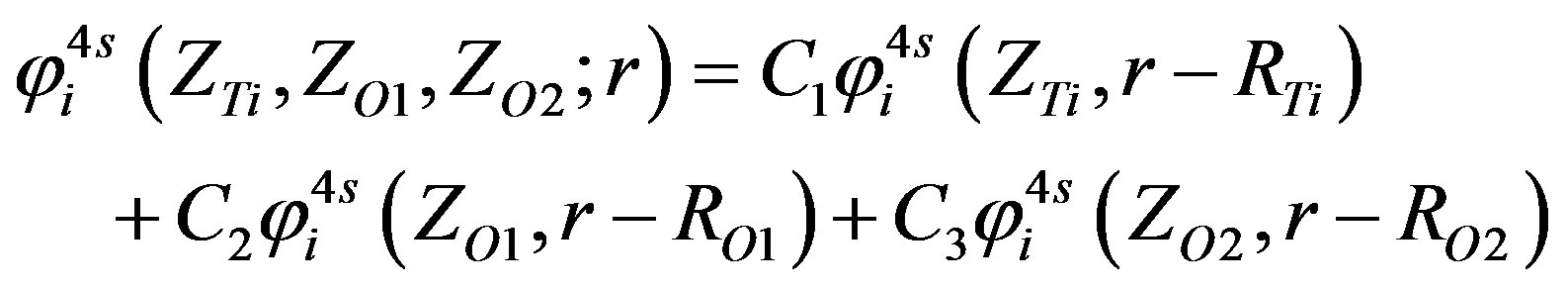 (16)
(16)
 (17)
(17)
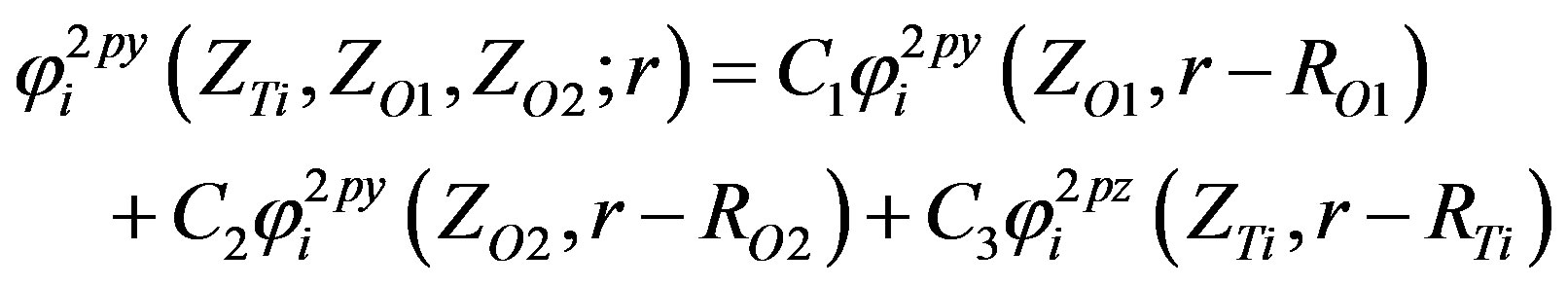 (18)
(18)
 (19)
(19)
where ,
, 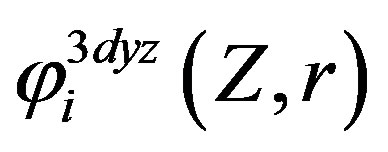 ,
,  ,
,  ,
, 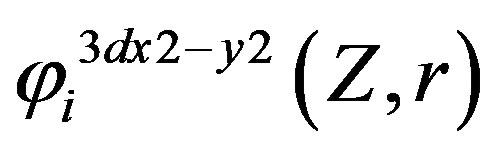 ,
,  ,
,  ,
, 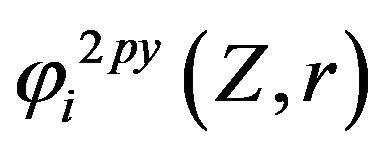 , and
, and 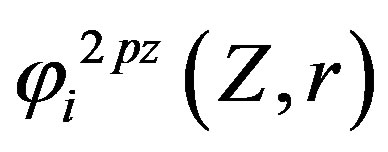 are Slater-type orbitals of atomic wave functions. r – RTi, r – RO1, and r – RO2 are distances of ith electron from titanium and from oxygens, respectively.
are Slater-type orbitals of atomic wave functions. r – RTi, r – RO1, and r – RO2 are distances of ith electron from titanium and from oxygens, respectively.
The single-particle wave function for the positron in the bound state with valance electrons of oxygen and titanium is a hybrid wave function of these electron wave functions. According to the principle of linear superposition, the single-particle wave function for positron is supposed to take the form
 (20)
(20)
where ZTi, ZO1, ZO2,  ,
,  and
and  are the variation parameters in the atomic wave function of electron and positron in TiO2; C1, C2 and C3 are the weighted coefficients of the electron wave function with
are the variation parameters in the atomic wave function of electron and positron in TiO2; C1, C2 and C3 are the weighted coefficients of the electron wave function with  ; and c1, c2, c3, c4, c5, c6, c7, c8 and c9 are the weighted coefficients of the positron wave function with
; and c1, c2, c3, c4, c5, c6, c7, c8 and c9 are the weighted coefficients of the positron wave function with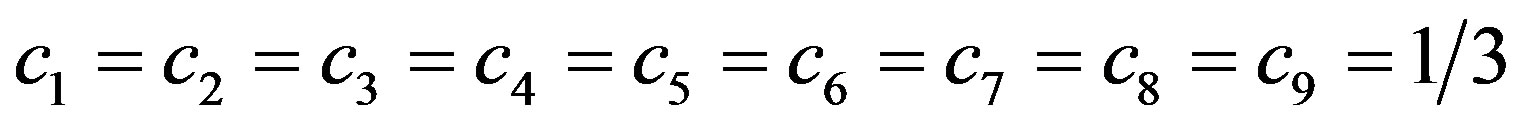 .
.
Using equations from (11) to (20) and (1) to (8), the minimized energy is calculated by VQMC to obtain the ground-state wave function of this system. Assuming that the ground-state wave function is valid for TiO2 rutile, the properties of electron-positron annihilation in TiO2 rutile, therefore, are determined.
3. Results and Discussion
To calculate the ground-state wave function of electrons and a positron in TiO2 molecule, fourteen sets of energy data corresponding to the variation of fourteen parameters ZTi, ZO1, ZO2, be, ae, Ae, Fe,  ,
, 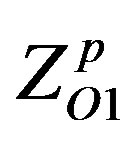 ,
,  , bep, aep, Aep, and Fep are generated. Each result is calculated by varying one of the parameters, and the other thirteen parameters are kept as constants. The set of optimized parameters, which make the trial wave function well approach to the exact wave function, is determined by minimizing energy of the system. These optimized parameters are given in Table 1.
, bep, aep, Aep, and Fep are generated. Each result is calculated by varying one of the parameters, and the other thirteen parameters are kept as constants. The set of optimized parameters, which make the trial wave function well approach to the exact wave function, is determined by minimizing energy of the system. These optimized parameters are given in Table 1.
The enhancement factor and positron lifetime in a perfect TiO2 rutile crystal are determined from these parameters. The electron-positron pair correlation distribution in the perfect rutile crystal of TiO2 is determined by Monte Carlo simulation as shown in Figure 2(a). The enhancement factor is extrapolated by a pair correlation function which is fitted to the Chebyshev polynomial in Equation (10). The number of coefficients, N, in Equation (10) is determined by minimizing the chi square of fitting goodness of the pair correlation function as shown in Figure 2(b). The minimal chi square corresponds to N = 41 with the value of chi square c2 of 0.255448 and the values of the coefficients are given in the Table 2. After fitting analytical form of pair correlation function of electron-positron 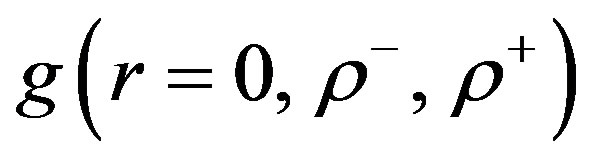 is constructed, the enhancement factor is calculated with
is constructed, the enhancement factor is calculated with  as shown in Figures 2(c) and (d). This enhancement factor can be considered as an effective number of electrons [10]. So the value of the enhancement factor is resonable in compare with the results in the Reference [10]. From Equation (9) and the enhancement factor, annihilation rate is estimated by an overlap of electron and positron densities. The calculation annihilation rate is G = (5.858 ± 0.007) × 109 (s−1). The positron lifetime is the inverse of the annihilation rate i = (170 ± 2) ps. The fitting parameters of the Chebyshev polynomial are shown on Table 2.
as shown in Figures 2(c) and (d). This enhancement factor can be considered as an effective number of electrons [10]. So the value of the enhancement factor is resonable in compare with the results in the Reference [10]. From Equation (9) and the enhancement factor, annihilation rate is estimated by an overlap of electron and positron densities. The calculation annihilation rate is G = (5.858 ± 0.007) × 109 (s−1). The positron lifetime is the inverse of the annihilation rate i = (170 ± 2) ps. The fitting parameters of the Chebyshev polynomial are shown on Table 2.
The enhancement factor and positron lifetime in TiO2 rutile crystal of an oxygen defect, created by removing one oxygen atom from a unit cell of TiO2 perfect rutile crystal, are also calculated from these parameters, which is assumed that they is still valid for the electron and positron wave functions in the TiO2 rutile crystal of an oxygen defect. The distribution of electron-positron pair correlation in the TiO2 of an oxygen defect is obtained from Monte Carlo simulation as shown in Figure 3(a). The number of coefficients, N, in this case is identified by the minimization of the chi square corresponding to N = 42 with the value of chi square c2 of 0.0542912 as shown in Figure 3(b) and the values of the coefficients are given in the Table 3. The enhancement factor in TiO2 of an oxygen defect is obtained by the extrapolation of the pair correlation function at r = 0 with  as shown in Figures 3(c) and (d). The annihilation rate and lifetime of positron, which are determined from this enhancement factor and the overlap of electron and positron densities, are G = (3.756 ± 0.006) × 109 (s−1) and i = (266 ± 3) ps, respectively. This positron lifetime is greater than the value in the perfect crystal of TiO2. It shows that this result is suitable to predict the positron lifetime in a monovacancy defect.
as shown in Figures 3(c) and (d). The annihilation rate and lifetime of positron, which are determined from this enhancement factor and the overlap of electron and positron densities, are G = (3.756 ± 0.006) × 109 (s−1) and i = (266 ± 3) ps, respectively. This positron lifetime is greater than the value in the perfect crystal of TiO2. It shows that this result is suitable to predict the positron lifetime in a monovacancy defect.
The enhancement factor and the positron lifetime in TiO2 rutile crystal of a titanium defect, created by removing one titanium atom from a unit cell of TiO2 perfect rutile crystal, are determined similarly. The wave function parameters of electron and positron in the TiO2 rutile crystal of a titanium defect is still valid, and the distribution of electron-positron pair correlation is obtained from Monte Carlo simulation as shown in Figure 4(a). The number of coefficients, N, is determined by the

Table 1. The values of optimized parameters of electron and positron wave function.
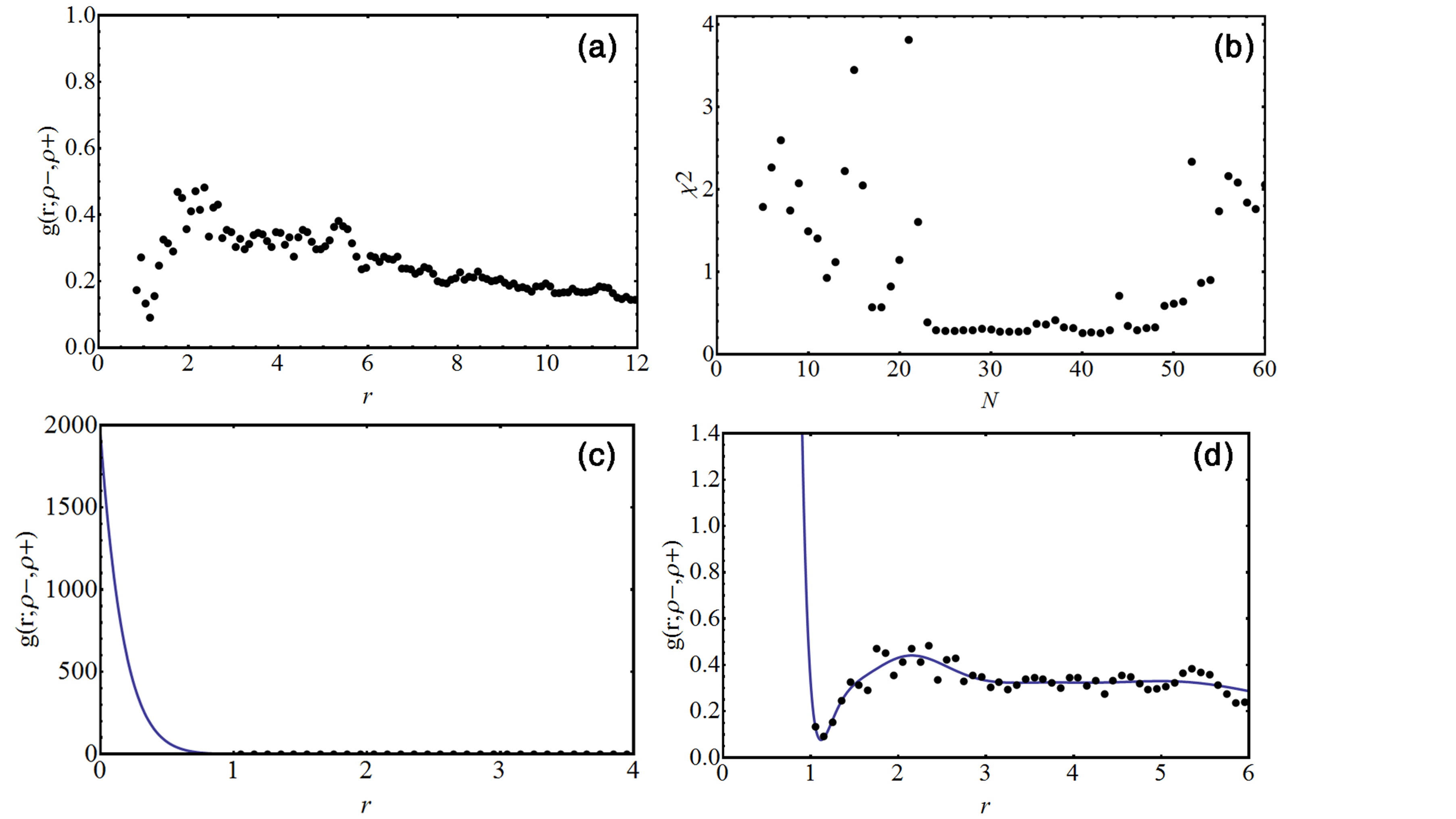
Figure 2. (a) The electron-positron pair distribution obtained by Monte Carlo simulation with the optimized wave function of electron and positron in TiO2 perfect rutile crystal; (b) The chi square of goodness of fit in the term of the number of Chebyshev coefficients; (c), (d) The fitted pair correlation fucntion of electron-positron in TiO2 perfect rutile crystal. The black dot is Monte Carlo simulation and the solid line is its fitting curve.
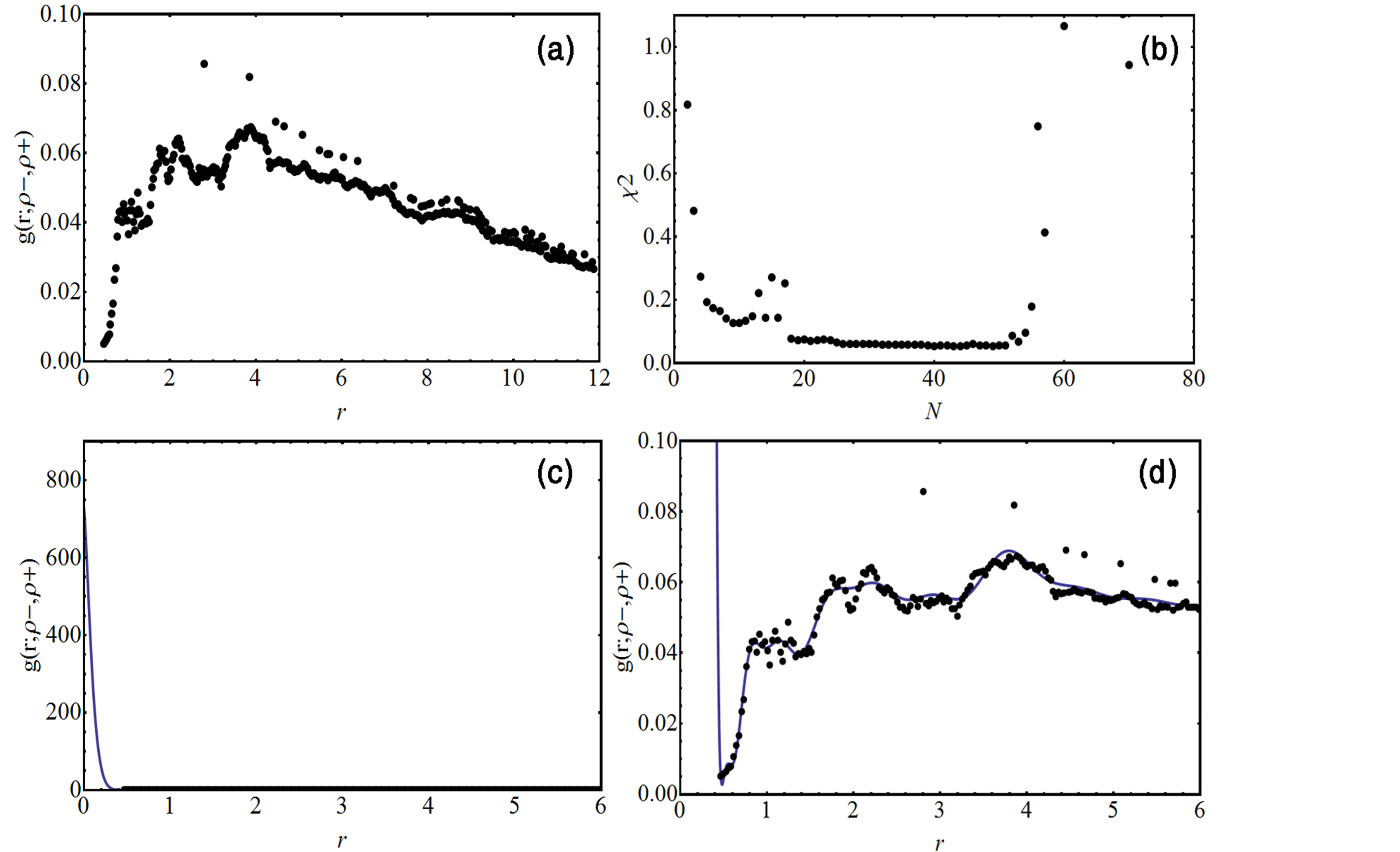
Figure 3. (a) The electron-positron pair distribution obtained by Monte Carlo simulation with the optimized wavefunction of electron and positron in TiO2 rutile crystal of an oxygen defect; (b) The chi square of goodness of fit in the term of the number of Chebyshev coefficients; (c), (d) The fitted pair correlation function of electron-positron in TiO2 rutile crystal of an oxygen defect. The black dot is Monte Carlo simulation and the solid line is its fitting curve.
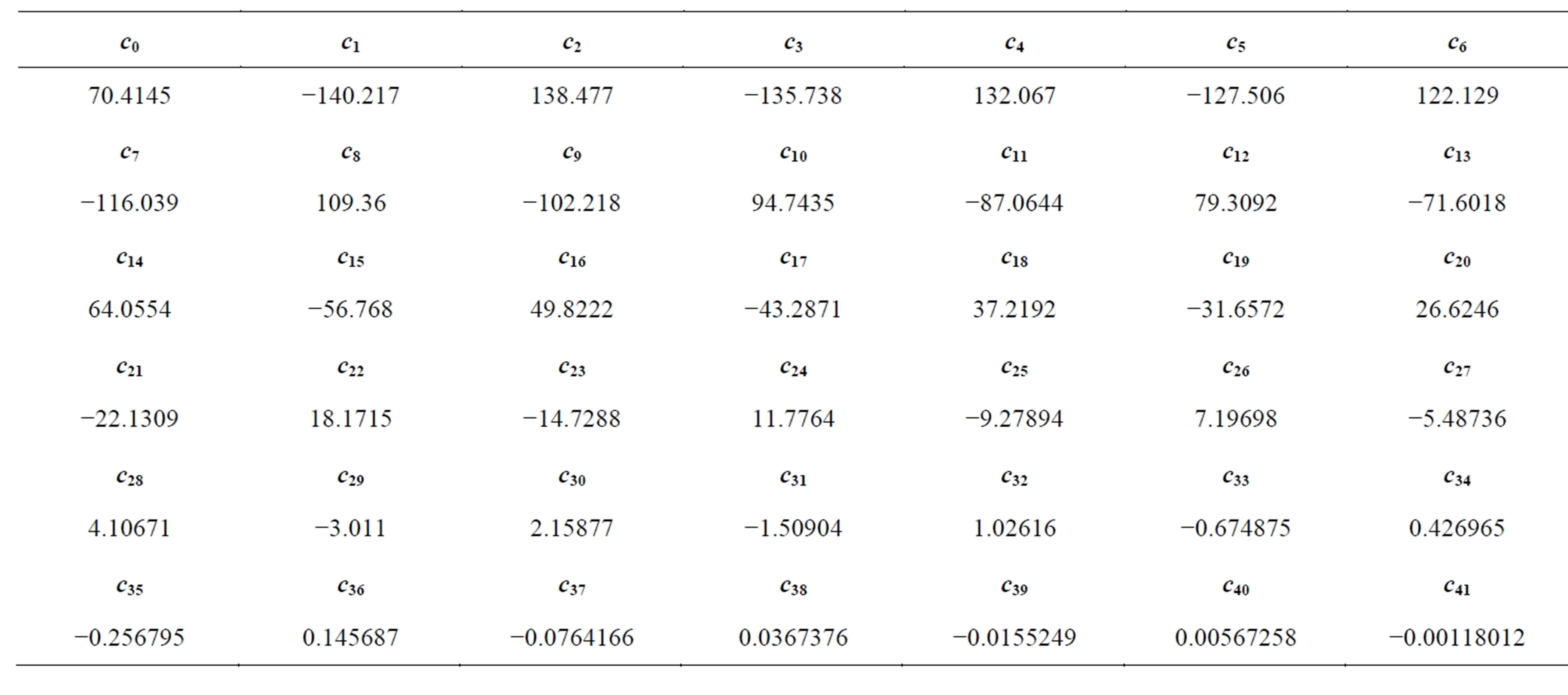
Table 2. The fitting parameters of the Chebyshev polynomial of electron-positron correlation function in TiO2 perfect rutile crystal.
minimization of chi square of fitting goodness of the pair correlation function as shown in Figure 4(b). The minimal chi square corresponds to N = 42 with the value of chi square c2 of 4.80132. The values of the coefficients are given in the Table 4. From this pair correlation function, the enhancement factor is calculated with  as shown in the Figures 4(c) and (d). The results of the annihilation rate and the positron lifetime are G = (4.109 ± 0.003) × 109 (s−1) and i = (243 ± 2) ps, respectively. This lifetime is as well greater than the positron lifetime in the perfect TiO2 crystal but it is smaller than the positron lifetime in the TiO2 of oxygen defect. The results of the positron lifetime in oxygen and tititanium defects in TiO2 rutile crystal are still in
as shown in the Figures 4(c) and (d). The results of the annihilation rate and the positron lifetime are G = (4.109 ± 0.003) × 109 (s−1) and i = (243 ± 2) ps, respectively. This lifetime is as well greater than the positron lifetime in the perfect TiO2 crystal but it is smaller than the positron lifetime in the TiO2 of oxygen defect. The results of the positron lifetime in oxygen and tititanium defects in TiO2 rutile crystal are still in
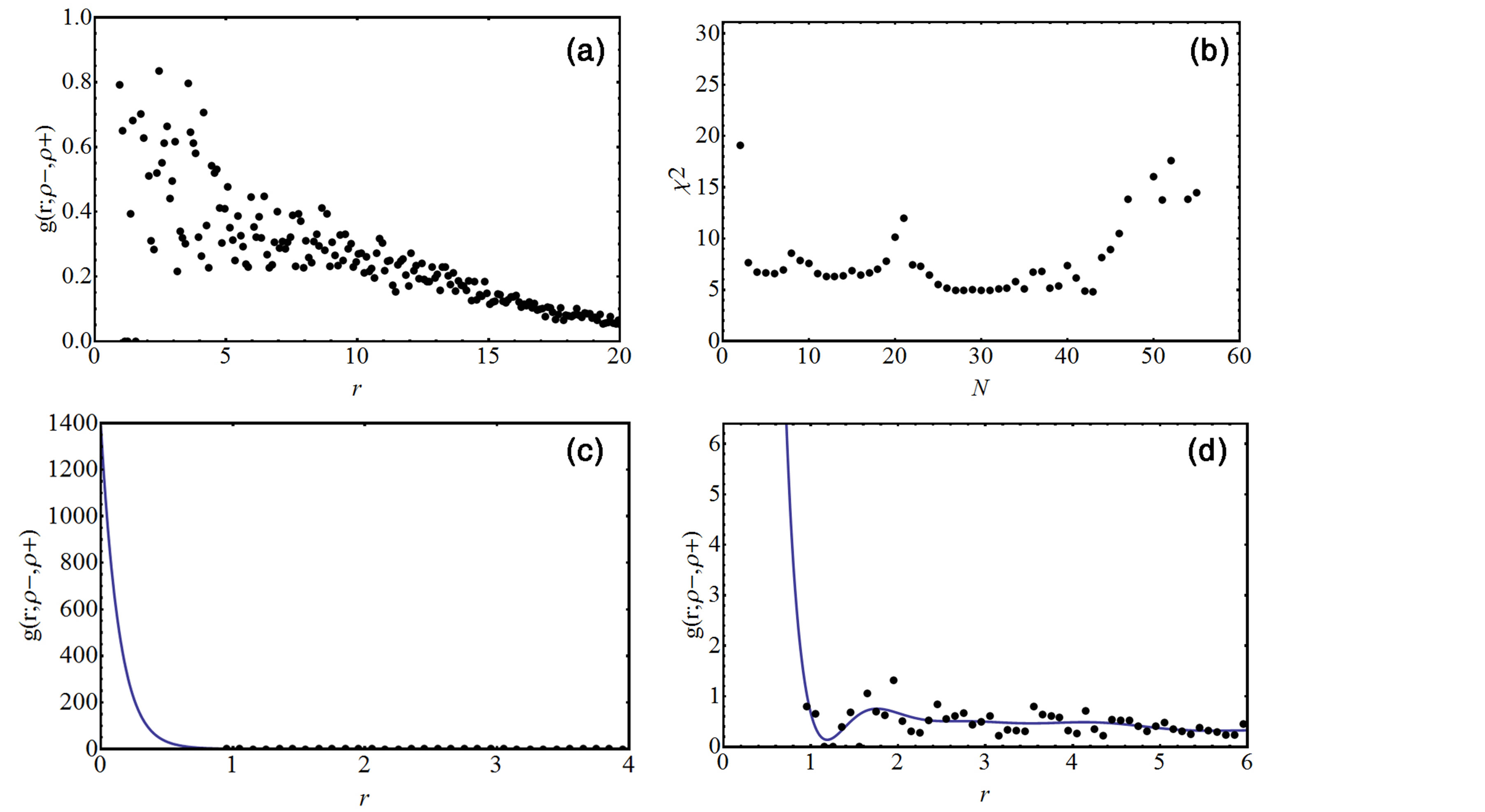
Figure 4. (a) The electron-positron pair distribution obtained by Monte Carlo simulation with the optimized wavefunction of electron and positron in TiO2 rutile crystal of a titanium defect; (b) The chi square of goodness of fit in the number of the Chebyshev coefficients; (c), (d) The fitted pair correlation fucntion of electron-positron in TiO2 rutile crystal of a titanium defect. The black dot is Monte Carlo simulation and the solid line is its fitting curve.
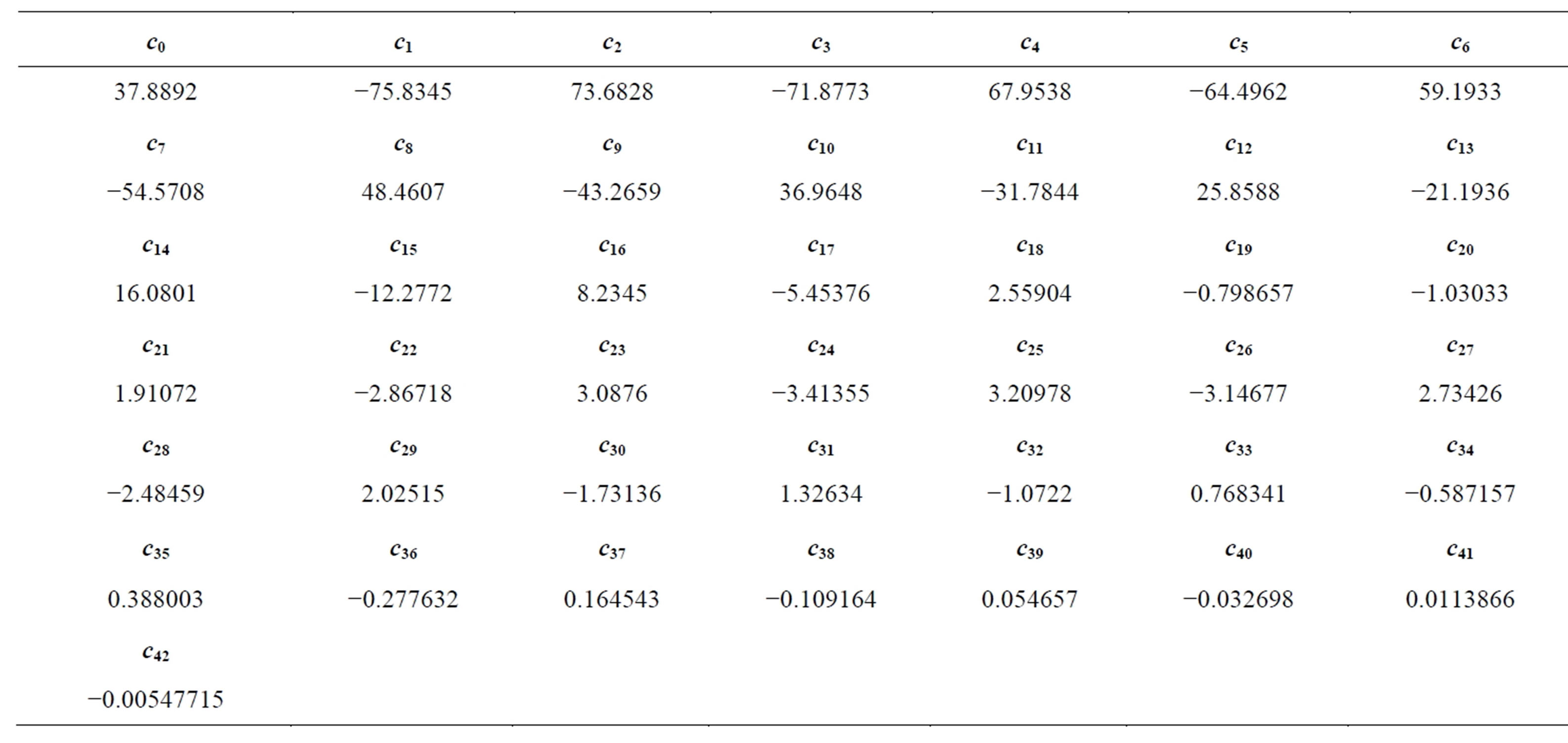
Table 3. The fitting parameters of the Chebyshev polynomial of electron-positron correlation function in TiO2 rutile crystal of an oxygen defect.
good agreement with shorter lifetime components of positron in the vacancies of TiO2 rutile [11].
4. Conclusions
Base on the principle of linear superposition, the KohnSham approximation, the Slater-type orbital, the modification of Jastrow and the VQMC method, we derived a theoretical model to determine the positron lifetime for some element-specific structure of materials.
In the scenario of purely theoretical calculations, we use real space electron and positron distributions to estimate the value of the positron lifetime in TiO2 rutile crystal structure. The calculation results show that the lifetime of a positron in the perfect crystal, i = 170 ps, is shorter than in the oxygen defect crystal, i = 266 ps, and

Table 4. The fitting parameters of the Chebyshev polynomial of electron-positron correlation function in TiO2 rutile crystal of a titanium defect.
the titanium defect crystal, i = 243 ps. In comparison with the experimental results, the positron lifetime of this calculation in the perfect crystal is also shorter than the short lifetime component of the positron in the vacancies of TiO2 rutile. However, the positron lifetimes of this calculation in the crystal of oxygen and titanium defects are still in good agreement with the positron lifetimes in the vacancies of TiO2 rutile. Therefore, the results can be used to predict lifetime components of positron in the perfect and defective TiO2 rutile crystal.
REFERENCES
- F. Jensen, “Introduction to Computational Chemistry,” John Wiley and Sons Ltd, Chichester, 2007.
- E. Boronski and R. M. Nieminen, “Electron-Positron Density-Functional Theory,” Physical Review B, Vol. 34, No. 6, 1985, pp. 3820-3831. http://dx.doi.org/10.1103/PhysRevB.34.3820
- H. Yukawa, “On the Interaction of Elementary Particles,” Progress of Theoretical Physics Supplement, Vol. 1, 1955, pp. 24-45. http://dx.doi.org/10.1143/PTPS.1.24
- W. Kohn and L. J. Sham, “Self-Consistent Equations Including Exchange and Correlation Effects,” Physical Review Journal, Vol. 140, No. 4A, 1965, pp. A1133-A1138. http://link.aps.org/doi/10.1103/PhysRev.140.A1133
- S. Daiuk, M. Sob and A. Rubaszek, “Theoretical calculations of positron annihilation with rare gas core electrons in simple and transition metals,” Journal of Physics F: Metal Physics B, Vol. 43, No. 4, 1991, pp. 2580-2593. http://link.aps.org/doi/10.1103/PhysRevB.43.2580
- M. J. Puska and R. M. Nieminen, “Defect Spectroscopy with Positron: A General Calculation Method,” Journal of Physics F: Metal Physics, 1983, pp. 333-346. http://dx.doi.org/10.1088/0305-4608/13/2/009
- A. Gil, J. Segura and N. Temme, “Numerical Methods for Special Functions,” Society for Industrial Mathematics, 3600 University Science Center, Philadelphia., 2007.
- N. W. Ashcroft and N. D. Mermin, “Solid State Physics,” Thomson Learning, Inc., 1976.
- V. Magnasco, “Methods of Molecular Quantum Mechanics,” John Wiley and Sons Ltd, Hoboken, 2009. http://dx.doi.org/10.1002/9780470684559
- G. F. Gribakin and C. M. R. Lee, “Application of the zero-range potential model to positron annihilation on molecules,” Nuclear Instruments and Methods in Physics Research B, Vol. 247, No. 1, 2006, pp. 31-37. http://dx.doi.org/10.1016/j.nimb.2006.01.035m
- E. M. Hassan, B. A. A. Balboul and M. A. Abdel-Rahman, “Probing the Phase Transition in Nanocrystalline TiO2 Powders by Positron Lifetime (PAL) Technique,” Defect and Diffusion Forum, Vol. 319-320, 2011, pp 151-159.

