American Journal of Operations Research
Vol.06 No.06(2016), Article ID:72145,9 pages
10.4236/ajor.2016.66044
Resolution of Resource Contentions in the CCPM-MPL Using Simulated Annealing and Genetic Algorithm
Hajime Yokoyama, Hiroyuki Goto
Department of Industrial & System Engineering, Hosei University, Tokyo, Japan
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 20, 2016; Accepted: November 18, 2016; Published: November 21, 2016
ABSTRACT
This research aims to plan a “good-enough” schedule with leveling of resource contentions. We use the existing critical chain project management-max-plus linear framework. Critical chain project management is known as a technique used to both shorten the makespan and observe the due date under limited resources; the max- plus linear representation is an approach for modeling discrete event systems as production systems and project scheduling. If a contention arises within a single resource, we must resolve it by appending precedence relations. Thus, the resolution framework is reduced to a combinatorial optimization. If we aim to obtain the exact optimal solution, the maximum computation time is longer than 10 hours for 20 jobs. We thus experiment with Simulated Annealing (SA) and Genetic Algorithm (GA) to obtain an approximate solution within a practical time. Comparing the two methods, the former was beneficial in computation time, whereas the latter was better in terms of the performance of the solution. If the number of tasks is 50, the solution using SA is better than that using GA.
Keywords:
Critical Chain Project Management, Max-Plus Algebra, CCPM-MPL, Simulated Annealing, Genetic Algorithm

1. Introduction
This research aims to plan a “good-enough” schedule with leveling of resource contentions. References [1] and [2] modified and extended a scheduling methodology referred to as critical chain project management-max-plus linear (CCPM-MPL), in which CCPM [3] [4] was applied to the max-plus algebra [5] . CCPM is a technique for project management invented by E. M. Goldratt and developed by L. P. Leach. The objective of this method is to both shorten the makespan and observe the due date under a limited number of resources. The max-plus algebra is an algebraic system wherein the max and plus operations are defined as addition and multiplication, respectively. MPL [1] representation is an approach for modeling and analyzing a class of discrete-event systems such as production and project scheduling, in which the behavior of the target system is represented by linear equations in the max-plus algebra. MPL representation can formulate systems with structures of non-concurrency, synchronization, parallel pro- cessing of multiple tasks, and so on [1] . We assume that a single resource cannot process multiple tasks simultaneously. If a contention arises within a single resource, we must resolve it by appending precedence relations. Thus, the resolution framework is reduced to a combinatorial problem. To level resource contentions, we developed a complete enumeration method by which an exact solution is obtained. In a numerical simulation, the maximum computation time was longer than 10 hours for 20 jobs. Reference [6] obtained a “good-enough” schedule by using Genetic Algorithm (GA) within a short computation time. On the other hand, we uncovered a preliminary design to obtain a “good-enough” schedule by using Simulated Annealing (SA) [7] . However, it is not currently clear which of the two methods is better. Hence, this research compares the two methods in terms of the performances of their solutions, computation times, and values.
2. CCPM-MPL Framework
After defining the max-plus algebra, we define the CCPM-MPL framework with the help of [1] and [2] .
2.1. Max-Plus Algebra
We define a set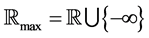 , where
, where 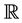 is the whole real line. Then, for
is the whole real line. Then, for 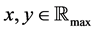 , we define the operators:
, we define the operators:
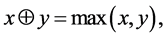 (1)
(1)
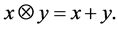 (2)
(2)
The priority of operator  is higher than that of
is higher than that of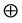 . If
. If 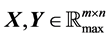 and
and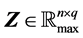 ,
,
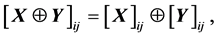 (3)
(3)
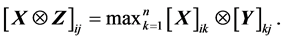 (4)
(4)
The zero and unit elements for operators 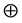 and
and  are denoted by
are denoted by 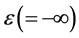 and
and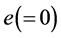 , respectively.
, respectively. 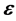 is a matrix whose elements are all
is a matrix whose elements are all , and
, and  is a matrix whose diagonal elements are
is a matrix whose diagonal elements are 




where 



2.2. Formulation of the CCPM-MPL Framework
We define the following relevant matrices and vectors:
・ n: number of tasks;
・ 
・ 
・ 

・ 

・ 

・ 

・ 

・ 

・ 

The earliest task-completion times of all tasks, 

where


Matrixes 



Then, the latest task-starting times, 

The latest input times, 


As a consequence, the total floats of all tasks can be calculated using Equations ((5) and (8)):

All tasks can be classified into two types: 




We then calculate two matrices, 


In the CCPM framework, there are two types of buffers, referred to as feeding and project buffers. The size of each buffer is calculated by


where

Feeding buffers are inserted wherever a non-critical task joins into a critical one. A project buffer is inserted on the eve of an output to avoid tardiness of the project. To reflect the insertion of the two types of buffers, we incur weights to the adjacency matrix 



Now we can calculate the earliest task-completion, 




Matrix 


We treat 

3. Resolution of Resource Contentions
We explain the resolution of resource contentions with the help of [8] . We add relevant matrices and vectors as follows:
・ 
・ 
・ 

We consider Figure 1 as an example project with five tasks before the leveling of resource contentions. The duration time of each task is


Tasks 1, 4, and 5 are processed by resource 1, whereas tasks 2 and 3 are processed by resource 2. If resource 2 processes tasks 2 and 3 simultaneously, a resource contention occurs. We avoid contentions between tasks 2 and 3 by appending two precedence relations, which are expressed by broken arrows in Figure 2, which shows the project after the resource contention is leveled. We then reflect the leveling of the resource contentions using the following adjacency matrix,

In addition, the processing order of tasks, 

Our numerical simulation to level resource contentions shows that the maximum
Figure 1. Example of a fifth-task project before a resource contention is leveled.
Figure 2. Example of the fifth-task project after the resource contention is leveled.
computation time was longer than 10 hours for 20 jobs. We thus consider the development of approximate methods within a short computation time.
4. Two Metaheuristics
We experiment with an optimization based on Genetic Algorithm (GA) and Simulated Annealing (SA), both of which are common metaheuristics.
4.1. Genetic Algorithm
We experiment with an optimization based on the GA developed in [6] , which is used to obtain an approximate solution.
Algorithm 1: Genetic Algorithm
STEP 1. Set mutation parameter and termination condition, 

STEP 2. Generate a random solution, 

STEP 3. Focusing on a row vector of 

STEP 4. If a mutation occurs having probability
STEP 5. Swap two tasks of 
STEP 6. Create the new earliest output times, 

STEP 7. If 


STEP 8. Terminate if the termination condition is satisfied. If otherwise, return to STEP4.
4.2. Simulated Annealing
SA [9] is known as an approach to efficiently obtain an approximate solution. We use the 2-opt neighborhood method [10] based on a local search to generate a neighboring solution.
Algorithm 2: Simulated Annealing
STEP 1. Initialize the temperature and cooling parameters, 

STEP 2. Generate a random solution, 

STEP 3. Generate a neighboring solution, 

STEP 4. Calculate
STEP 5. If 






STEP 6. Update the temperature parameter,


STEP 7. Repeat STEPS3-6.
STEP 8. Terminate if the temperatures are sufficiently low. If otherwise, return to STEP3.
5. Approximate Ratio and Computation Time
We obtain solutions using the SA- and GA-based algorithms. We use a personal computer with the following execution environment:
・ machine: Dell Optiplex 9020;
・ CPU: Intel® Core™ i7-4790 3.60 GHz;
・ OS: Microsoft Windows 7 Professional;
・ memory: 4.0 GB;
・ programming language: MATLAB R2015b.
The test cases for the numerical experiment are generated under the following conditions:
・ number of cases: 100;
・ number of resources,
・ number of resources for task,
・ duration time,
We obtain approximate solutions using two metaheuristics. The temperature and cooling parameter are set to 



Table 1. Performance of the solutions.
Table 2. Average values of the solutions.
Figure 3. Average computation times in seconds.
here that the solution using the SA-based algorithm is better than that using the GA if the number of tasks is 50.
6. Conclusions
This research has studied the planning of a “good-enough” schedule with leveling of resource contentions. We utilized an existing framework called the CCPM-MPL. The resolution framework was reduced to a combinatorial problem. We used SA- and GA-based algorithms to obtain approximate solutions within short time. Moreover, we used the 2-opt neighborhood to generate a neighboring solution in the SA-based algorithm. Comparing the two methods, the SA-based algorithm was beneficial in terms of computation time, whereas the latter was better in terms of the performance of the solution. In addition, when the number of tasks was 50, the value of the solution using the SA-based algorithm was better than that using the GA-based algorithm.
Developing an original heuristic to level resource contentions within a short computation time is our future work.
Cite this paper
Yokoyama, H. and Goto, H. (2016) Resolution of Resource Contentions in the CCPM-MPL Using Simulated Annealing and Genetic Algorithm. American Journal of Operations Research, 6, 480-488. http://dx.doi.org/10.4236/ajor.2016.66044
References
- 1. Goto, H. (2017) Forward-Compatible Framework with Critical-Chain Project Management using a Max-Plus Linear Representation. OPSEARCH, 54, 16 p..
http://dx.doi.org/10.1007/s12597-016-0276-3 - 2. Goto, H., Truc, N.T.N. and Takahashi, H. (2013) Simple Representation of the Critical Chain Project Management Framework in a Max-Plus Linear Form. SICE Journal of Control, Measurement, and System Integration, 6, 341-344.
http://dx.doi.org/10.9746/jcmsi.6.341 - 3. Goldratt, E.M. (1997) Critical Chain. North River Press, Great Barrington.
- 4. Leach, L.P. (2005) Critical Chain Project Management. 2nd Edition, Artech House, Boston.
- 5. Heidergott, B., Olsder, G.J. and Woude, L. (2006) Max Plus at Work: Modeling and Analysis of Synchronized Systems. Princeton University Press, New Jersey.
- 6. Koga, H., Goto, H. and Chiba, E. (2014) Resolution of Resource Conflicts in the CCPM Framework: Utilization of a Local Search Method or Genetic Algorithm, 50, 7-12. (In Japanese)
- 7. Yokoyama, H. and Goto, H. (2016) Resolution of Resource Contentions in the Critical Chain Project Management Based on Simulated Annealing. Proceedings of the 6th International Conference on Industrial Engineering and Operations Management, Kuala Lumpur, 8 March 2016, 29.
- 8. Koga, H., Goto, H. and Chiba, E. (2014) Resolution of Resource Conflicts in the CCPM Framework Using a Local Search Method. Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Bandar Sunway, 10 December 2014, 94-98.
http://dx.doi.org/10.1109/ieem.2014.7058607 - 9. Kirkpatrick, S., Gelatt, C.D. and Vecchi, M.P. (1983) Optimization by Simulated Annealing. Science, 220, 671-680.
http://dx.doi.org/10.1126/science.220.4598.671 - 10. Croes, G.A. (1958) A Method for Solving Traveling-Salesman Problems. Operation Research, 6, 791-812.
http://dx.doi.org/10.1287/opre.6.6.791





