American Journal of Operations Research
Vol.4 No.3(2014), Article ID:45684,9 pages DOI:10.4236/ajor.2014.43015
A Linear Programming Approach for Parallel Cell Scheduling with Sequence-Dependent Setup Times
Tuğba Yıldız, Besim Türker Özalp, İlker Küçükoğlu, Alkın Yurtkuran, Nursel Öztürk
Industrial Engineering Department, Faculty of Engineering, Uludag University, Bursa, Turkey
Email: tugbayildiz08@gmail.com, tozalp@uludag.edu.tr, ikucukoglu@uludag.edu.tr, alkin@uludag.edu.tr, nursel@uludag.edu.tr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 March 2014; revised 12 April 2014; accepted 19 April 2014
ABSTRACT
In this study, we consider the problem of scheduling a set of jobs with sequence-dependent setup times on a set of parallel production cells. The objective of this study is to minimize the total completion time. We note that total customer demands for each type should be satisfied, and total required production time in each cell cannot exceed the capacity of the cell. This problem is formulated as an integer programming model and an interface is designed to provide integrity between data and software. Mathematical model is tested by both randomly generated data set and realworld data set from a factory that produce automotive components. As a result of this study, the solution which gives the best alternative production schedule is obtained.
Keywords:Production Scheduling, Total Completion Time, Sequence Dependent Setup Times

1. Introduction
Production scheduling is one of the major issues in production planning as it has an effect on productivity. Each combination of production sequence could have different completion time, in this point to find optimum combination is very important for a company in today’s competitive market place, and if company has a lot of different product types with different processing time and/or if each of them needs setup time, to find optimum sequence could be difficult or impossible with estimation or intuition. Stoop and Wiers have mentioned that the task of scheduling production units can become very complicated. Humans are not well equipped to control or optimize large and complex systems. Due to these reasons, techniques and information systems are commonly regarded as means to improve scheduling [1] .
The first systematic approach to scheduling problems was undertaken in the mid-1950s. After this approach, a lot of papers on different scheduling problems have appeared in the literature, and most of them assumed that the setup time can be ignored or reckoned as the job processing time. This assumption simplifies the analysis, however it affects the solution quality of scheduling that requires setup times [2] .
The setup times in scheduling problems were considered as separate after mid-1960s. Yang and Liao extensively researched all types of scheduling problems with setup times [3] . Cheng et al. reviewed flow shop scheduling problems [4] . Potts and Kovalyov surveyed scheduling problems with batching [5] . After these studies there has been a significant increase in publication of scheduling problems with setup times.
Allahverdi et al. classified scheduling problems with setup times as batch and non-batch. A batch setup time occurs when jobs are processed in batches (pallets, containers, boxes) and a setup of a certain time or cost precedes the processing of each batch. In a non-batch processing environment, a setup time is incurred prior to the processing of each job. The corresponding model can also be viewed as a batch setup time model in which each family consists of a single job. And also they classified batch and non-batch scheduling problems as sequencedependent and sequence-independent. It is sequence-dependent if its duration depends on the families of both the current and the immediately preceding batches, and is sequence-independent if its duration depends solely on the family of the current batch to be processed. All these classifications are valid in both a single machine and parallel machines problems [2] .
Bigras et al. worked on scheduling problems on a single machine in a sequence dependent setup times. They extended time-dependent travelling salesman problem to single machine scheduling problems with sequence dependent setup times [6] . Ng et al. studied a problem of scheduling n jobs in a single machine in batches. They assumed that a batch is a set of jobs processed contiguously and completed together when the processing of all jobs in the batch is finished and processing of a batch requires a machine setup time dependent on the position of this batch in the batch sequence [7] . Gagne et al. compared several heuristics for solving a single machine scheduling problem with sequence-dependent setup times. They describe an ant colony optimization algorithm, genetic algorithm, a simulated annealing approach, a local search method and a branch-and-bound algorithm [8] .
Haung et al. addressed the problem of scheduling on parallel machines in which the setup time is sequencedependent. They formulated the problem as an integer program and for the general cases they developed a hybrid genetic algorithm [9] . Tahar et al. suggest a heuristic algorithm for the problem of scheduling a set of jobs with sequence-dependent setup times on a set of parallel machines by using a linear programming modeling with setup times and job splitting [10] . Gacias et al. proposed a branch-and-bound method and heuristics based on discrepancy-based search methods for the parallel machine scheduling problem with precedence constraints and setup times [11] .
This paper can contribute both academic researches and business life. A developed mathematical model was used to find an optimum solution to a real-world problem. Parallel machine scheduling with sequence dependent setup times and minimization of the sum of the completion time is considered.
2. Problem Description and Mathematical Formulation
In our problem, customer demands dm for each product type m ![]() are produced in monthly basis without exceeding cell capacity hl for each cell l
are produced in monthly basis without exceeding cell capacity hl for each cell l ![]() and a type batch cannot split, because each job splitting requires additional setup time.
and a type batch cannot split, because each job splitting requires additional setup time.
In this problem, n product types ![]() must be scheduled on w
must be scheduled on w ![]() production cells. However, when a cell switches the production from a product type k
production cells. However, when a cell switches the production from a product type k ![]() to a product type m
to a product type m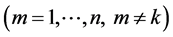 , a set up time ak,m ≥ 0 is required. Without loss of generality, we set ak,k = 0
, a set up time ak,m ≥ 0 is required. Without loss of generality, we set ak,k = 0![]() and to be able to start the production order we define a dummy product type, product type 0. With this assumption, we define a setup time for all product types which are produced immediately after product type 0. We assume that if a product type is scheduled at the beginning of the schedule, the average time setup time is taken.
and to be able to start the production order we define a dummy product type, product type 0. With this assumption, we define a setup time for all product types which are produced immediately after product type 0. We assume that if a product type is scheduled at the beginning of the schedule, the average time setup time is taken.
All the processing times of each product type m ![]() in cell l
in cell l ![]() which are defined as
which are defined as 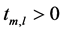 are our data that we use as inputs of this scheduling problem.
are our data that we use as inputs of this scheduling problem.
With the introduction of decision variable
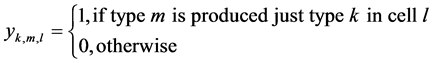
and status variables
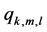 : the number of type m that produce just after type k in cell l
: the number of type m that produce just after type k in cell l
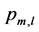 : total number of type m which is produced in cell l
: total number of type m which is produced in cell l
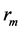 : total number of type m which is produced in all cell
: total number of type m which is produced in all cell
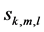 : producing time of
: producing time of 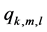
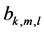 : sum of producing time qk,m,l and setup time to produce type m just after type k
: sum of producing time qk,m,l and setup time to produce type m just after type k
![]() : total required time for type m for production and setup in cell l
: total required time for type m for production and setup in cell l
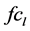 : total required time for all types which are assigned to cell l the problem can be formulated as follows (M in the formulation is a large positive number):
: total required time for all types which are assigned to cell l the problem can be formulated as follows (M in the formulation is a large positive number):
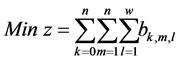
Subject to
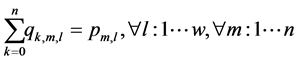 (1)
(1)
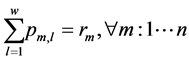 (2)
(2)
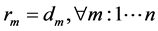 (3)
(3)
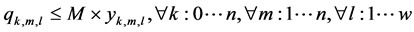 (4)
(4)
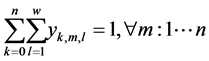 (5)
(5)
 (6)
(6)
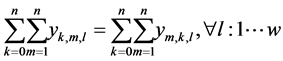 (7)
(7)
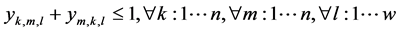 (8)
(8)
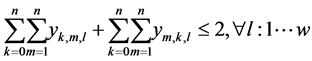 (9)
(9)
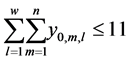 (10)
(10)
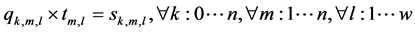 (11)
(11)
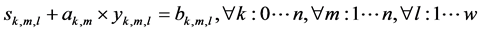 (12)
(12)
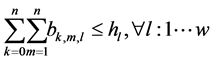 (13)
(13)
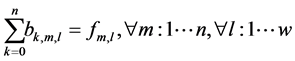 (14)
(14)
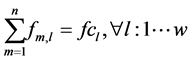 (15)
(15)
The objective is to minimize the total production time in all cells. Constraint (1) ensures that total quantity of type m which are assigned to cell l is equal to total number of type m which are produced in cell l in any sequence combinations of type m with type k. Constraint (2) and (3) guarantee that all customer demands will be satisfied. Constraint (4) provides link between assignment and sequence. To see with which part type the schedule starts we defined a dummy type number, type 0. With the help of constraint (5) the production schedule starts with type 0, so that the part type which comes just after type 0 is real type that production schedule starts with it. Constraint (6) and (7) ensure consecutive sequence among types. Constraint (8) guarantees that if a product type is assigned to a cell all parts of that type are produced in one sequence. Constraint (9) ensures that maximum one type can be produced after a part and maximum one type can be produced before the type. To meet the demand, Constraint (10) guarantees minimizing the cell number. To calculate production time of a product type which is assigned to a cell we defined constraint (11) and to add setup time to production time we defined constraint (12). Constraint (13) guarantees that total time of all parts assigned a cell cannot exceed the capacity of this cell. To see the total required time for a type m that is assigned to cell l, we defined constraint (14) and to see the total required time to produce all types which are assigned to cell l, we defined constraint (15).
3. An Illustrative Example
In order to illustrate the method based on linear programming, we consider an example with 15 jobs and 11 production cells and the mathematical model for 15 types and 11 cells is solved with Mathematical Programming Language (MPL) software.
Demands based on product types are given in Table 1, capacities of each cell are given in Table 2, and setup time matrix between product types is represented in Table 3. For instance, if product type 2 is produced right after type 1, 3000 seconds needed to prepare a cell for type 2. The unit processing time matrix is given in Table 4 and the results are transferred to Excel sheet by export command of MPL and the results are given in Table 5.
Table 1. Demands of product types.
Table 2. Capacities of production cells.
Table 3. Setup time matrix akm (s).
Table 4. Unit Processing time matrix tml (s).
Table 5. The results of fifteen-job-example.
Table 5 indicates the sequence of part types based on cell numbers to provide the minimum total completion time and production times of each type. The results demonstrate that 15 parts can produced in cell 3, 4, and 6 that gives minimum total completion time. According to Table 5, the type sequence in cell 4 {1, 3, 2, 5, 10}, in cell 6 {4, 14, 7, 15, 9, 8, 6}, and in cell 3 {11, 13, 12} give the optimum results. In addition to these results the number of each product type demands can be seen on Table 5.
4. Real-World Problem
In this section, a real-world example is used to evaluate the performance of the model. To illustrate the effectiveness of the mathematical model, we compare the results with current production scheduling results.
This study is completed in an automotive injector factory, in body section. Body section has four main processes which are turning, milling, heat treatment, and special process. Within this project we studied in turning process which is the first step of all body section as a pilot. Turning process has 35 different part types and 11 production cells.
4.1. Current Situation
Demands and assignments in current situation are given in Table 6. With the data given in Table 6, we calculate processing times of each type and then we calculate total production time, sum of setup time and processing time, of all types. Table 6 demonstrates that 2819 hours is needed to produce all types regarding to current sequence table.
Table 6. Demands, assignments and processing times of current situation.
4.2. Proposed Situation
Demands and assignments in current situation are given in Table 6. With the data given in Table 6, we calculate processing times of each type and then we calculate total production time, sum of setup time and processing time, of all types. Table 6 demonstrates that 2819 hours is needed to produce all types regarding to current sequence table.
The linear mathematical program with the same demands in current situation is run by MPL and results summarized as it is seen in Table 7. Production times in Table 7 consist of processing time and setup time.
According to Table 7, the sequence in cell 1 {19, 7, 18}, in cell 2 {35, 23, 29,}, in cell 4 {8, 6, 16}, in cell 5 {17, 3, 5, 9, 14, 24, 34, 33, 15, 30}, in cell 6 {32, 4, 25, 11, 20}, in cell 7 {13, 1, 2, 10, 12, 22, 21}, and in cell 8 {28, 26, 27, 31} gives the optimum results and the total production time is 2553 hours.
5. Conclusions
In this paper, we have proposed a new method based on linear programming for a parallel machine scheduling problem involving sequence dependent setup times. The criterion is to minimize the total production time. As shown in the real world problem section, total production time reduced from 2819 to 2553 hour. For this problem, average saving based on total production time is 9.4%, and due to the fact that demands are changing every month, the saving will change every month.
Figure 1 displays the variation of production times that are constructed by summation of processing and setup times for each type. It can be inspected from the figure that significant reduction in production times can be observed for the types where the demand is low (e.g. Type 11). Contrarily for the types where demands are distinctively higher (e.g. Type 20), it is hard to observe any significant change in the production times. According to this graphic, it can be concluded that the firm has found a proper assignment for high demand product types. As displayed in Figure 2, variations in setup times show significant reduction for the future situation versus the current one. For large majority of the product types, setup times decrease explicitly where the commentary for this situation should be the appropriate transition of product types according to the objective of this scheduling problem.
Table 7. Results of linear mathematical programming.
Another prominent gain is the usage of 8 production cells instead of 11 observed in the current situation. This is achieved by our linear programming approach with optimal product type assignments into production cells.
Topic of a future research is to apply heuristic methods; such as tabu search or simulated annealing algorithm for more product types. Because it is difficult to solve sequence-dependent scheduling problem for more product types.
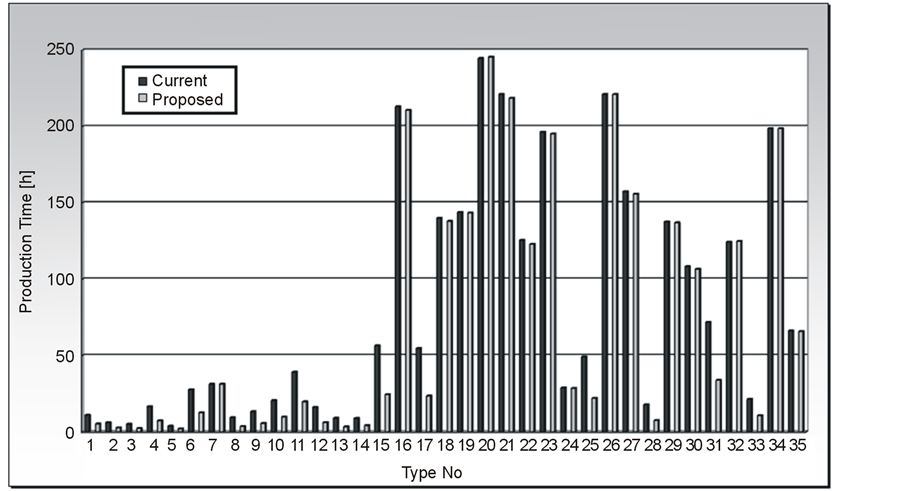
Figure 1. Comparison of production times [h] (Current vs. Proposed).
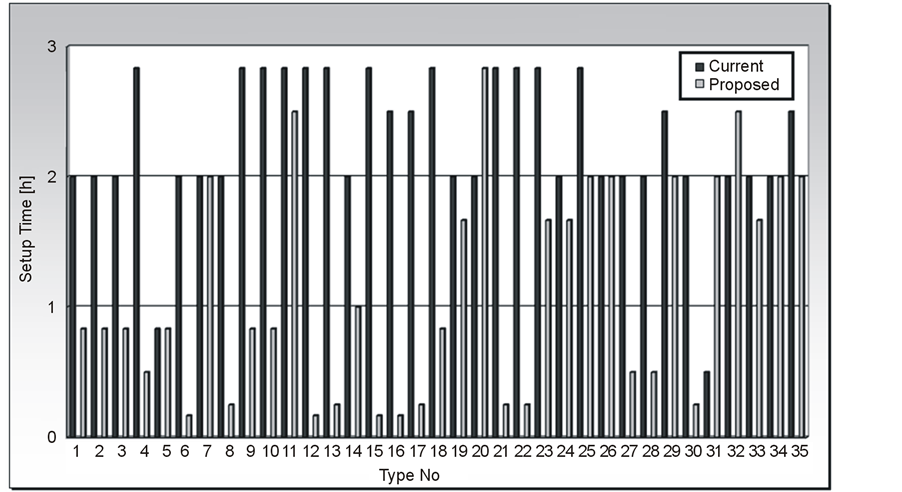
Figure 2. Comparison of setup times [h] (Current vs. Proposed).
Acknowledgements
The authors thank BOSCH Bursa Factory for providing data for the problem.
References
- Stoop, P. P. M. and Wiers, V.C.S. (1996) The Complexity of Scheduling in Practice. International Journal of Operations and Production Management, 16, 37-53. http://dx.doi.org/10.1108/01443579610130682
- Allahverdi, A., Ng, C.T., Cheng, T.C.E. and Kovalyov, M.Y. (2008) Survey of Scheduling Problems with Setup Times or Costs. European Journal of Operational Research, 187, 985-1032. http://dx.doi.org/10.1016/j.ejor.2006.06.060
- Yang, W.H. and Liao, C.J. (1999) Survey of Scheduling Research Involving Setup Times. International Journal of Systems Science, 30, 143-155. http://dx.doi.org/10.1080/002077299292498
- Cheng, T.C.E., Gupta, J.N.D. and Wang, G. (2000) A Review of Flowshop Scheduling Research with Setup Times. Production and Operations Management, 9, 262-282. http://dx.doi.org/10.1111/j.1937-5956.2000.tb00137.x
- Potts, C.N. and Kovalyov, M.Y. (2000) Scheduling with Batching: A Review. European Journal of Operational Research, 120, 228-349. http://dx.doi.org/10.1016/S0377-2217(99)00153-8
- Bigras, L.P., Gamache, M. and Savard, G. (2008) The Time-Dependent Travelling Salesman Problem and Single Machine Scheduling Problems with Sequence Dependent Setup Times. Discrete Optimization, 5, 685-699. http://dx.doi.org/10.1016/j.disopt.2008.04.001
- Ng, C.T., Cheng, T.C.E. and Kovalyov, M.Y. (2003) Batch Scheduling with Controllable Setup and Processing Times to Minimize Total Completion Time. Journal of the Operational Research Society, 54, 499-506. http://dx.doi.org/10.1057/palgrave.jors.2601537
- Gagne, C., Price, W.L. and Gravel, M. (2002) Comparing an ACO Algorithm with Other Heuristics for the Single Machine Scheduling Problem with Sequence-Dependent Setup Times. Journal of the Operational Research Society, 53, 895-906. http://dx.doi.org/10.1057/palgrave.jors.2601390
- Haung, S., Cai, L. and Zhang, X. (2009) Parallel Dedicated Machine Scheduling Problem with Sequence-Dependent Setups and a Single Server. Computers and Industrial Engineering, 58, 165-174. http://dx.doi.org/10.1016/j.cie.2009.10.003
- Tahar, D.N., Yalaoui, F., Chu, C. and Amodeo, L. (2005) A Linear Programming Approach for Identical Parallel Machine Scheduling with Job Splitting and Sequence-Dependent Setup Times. International Journal of Production Economics, 99, 63-73. http://dx.doi.org/10.1016/j.ijpe.2004.12.007
- Gacias, B., Artigues, C. and Lopez, P. (2010) Parallel Machine Scheduling with Precedence Constraints and Setup Times. Computers and Operations Research, 37, 2141-2151. http://dx.doi.org/10.1016/j.cor.2010.03.003


