American Journal of Operations Research
Vol.3 No.6(2013), Article ID:38601,9 pages DOI:10.4236/ajor.2013.36048
A Computational Comparison of Basis Updating Schemes for the Simplex Algorithm on a CPU-GPU System
Department of Applied Informatics, School of Information Sciences, University of Macedonia, Thessaloniki, Greece
Email: *ploskas@uom.gr
Copyright © 2013 Nikolaos Ploskas, Nikolaos Samaras. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 19, 2013; revised September 19, 2013; accepted September 29, 2013
Keywords: Simplex Algorithm; Basis Inverse; Graphics Processing Unit; MATLAB; Compute Unified Device Architecture
ABSTRACT
The computation of the basis inverse is the most time-consuming step in simplex type algorithms. This inverse does not have to be computed from scratch at any iteration, but updating schemes can be applied to accelerate this calculation. In this paper, we perform a computational comparison in which the basis inverse is computed with five different updating schemes. Then, we propose a parallel implementation of two updating schemes on a CPU-GPU System using MATLAB and CUDA environment. Finally, a computational study on randomly generated full dense linear programs is presented to establish the practical value of GPU-based implementation.
1. Introduction
Linear Programming (LP) is the process of minimizing or maximizing a linear objective function to a number of linear equality and inequality constraints. Simplex algorithm is the most widely used method for solving Linear Programming problems (LPs). Consider the following linear programming problem in the standard form shown in Equation (1):
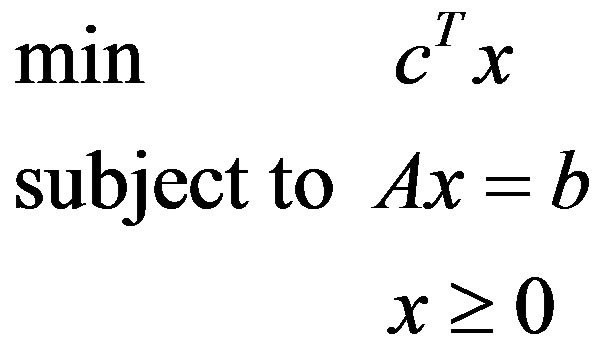 (1)
(1)
where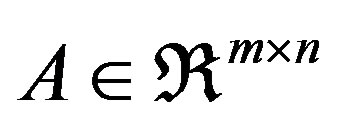 ,
, 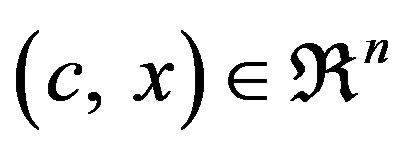 ,
, 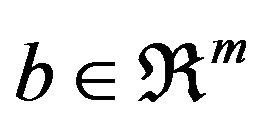 , and T denotes transposition. We assume that A has full rank, rank(A) = m, m < n. Consequently, the linear system Ax = b is consistent. The simplex algorithm searches for an optimal solution by moving from one feasible solution to another, along the edges of the feasible set. The dual problem associated with the linear problem in Equation (1) is shown in Equation (2):
, and T denotes transposition. We assume that A has full rank, rank(A) = m, m < n. Consequently, the linear system Ax = b is consistent. The simplex algorithm searches for an optimal solution by moving from one feasible solution to another, along the edges of the feasible set. The dual problem associated with the linear problem in Equation (1) is shown in Equation (2):
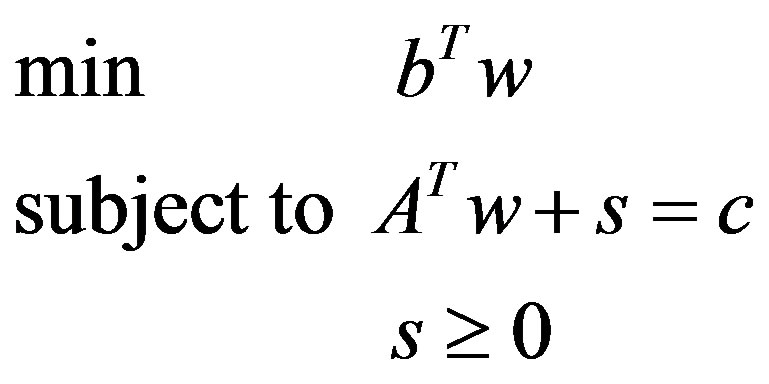 (2)
(2)
where 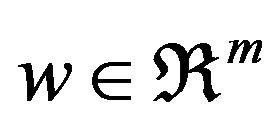 and
and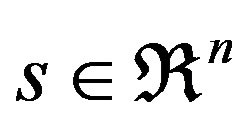 .
.
The past twenty years have been a time of remarkable developments in optimization solvers. Real life LPs tend to be large in size. A growing number of problems demand parallel computing capabilities. The explosion in computational power (CPUs and GPUs) has made it possible to solve large and difficult LPs in a short amount of time. As in the solution of any large scale mathematical system, the computational time for large LPs is a major concern. The basis inverse dictates the total computational effort of an iteration of simplex type algorithms. This inverse does not have to be computed from scratch at any iteration, but can be updated through a number of updating schemes. All efficient versions of the simplex algorithm work with some factorization of the basis matrix B or its inverse B−1.
Dantzig and Orchard-Hays [1] have proposed the Product Form of the Inverse (PFI), which maintains the basis inverse using a set of eta vectors. Benhamadou [2] proposed a Modification of the Product Form of the Inverse (MPFI). The key idea is that the current basis inverse 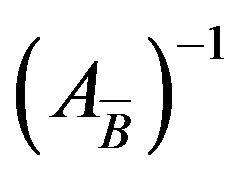 can be computed from the previous inverse
can be computed from the previous inverse 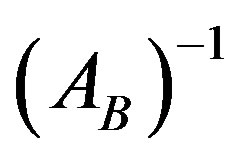 using a simple outer product of two vectors and one matrix addition.
using a simple outer product of two vectors and one matrix addition.
LU decomposition produces generally sparser factorizations than PFI [3]. The LU factorization for the basis inverse has been proposed by Markowitz [4]. Markowitz used LU decomposition to fully invert a matrix, but used the PFI scheme to update the basis inverse during simplex iterations. Bartels and Golub [5] have later proposed a scheme to update a sparse factorization, which was more stable than using PFI. Their computational experiments, however, proved that it was more computationally expensive. Forrest and Tomlin [6] created a variant of the Bartels-Golub method by sacrificing some stability characteristics causing the algorithm to have a smaller growth rate in the number of non-zero elements relative to the PFI scheme. Reid [7] proposed two variants of the Bartels-Golub updating scheme that aim to balance the sparsity and the numerical stability of the factorization. A variant of the Forrest-Tomlin update was proposed by Suhl and Suhl [8]. Other important updating techniques can be found in Saunders [9] and Goldfarb [10]. A full description of most of these updating methods can be found in Nazareth [11] and Chvátal [12].
There have been many reviews and variants of these methods individually, but only a few comparisons between them that are either obsolete or don’t compare all these updating schemes. McCoy and Tomlin [13] report the results of some experiments on measuring the accuracy of the PFI scheme, Bartels-Golub method and ForrestTomlin scheme. Lim et al. [14] provide a comparative study between Bartels-Golub method, Forrest-Tomlin method and Reid method. Badr et al. [15] perform a computational evaluation of PFI and MPFI updating schemes. Ploskas et al. [16] compare PFI and MPFI updating schemes both on their serial and their parallel implementation.
Originally, GPUs used to accelerate graphics rendering. GPUs have gained recently a lot of popularity and High Performance Computing applications have already started to use them. The computational capabilities of GPUs exceed the one of CPUs. GPU is utilized for data parallel and computationally intensive portions of an algorithm. NVIDIA introduced Compute Unified Device Architecture (CUDA) in late 2006. CUDA enables users to execute codes on their GPUs and it is based on a SIMT programming model. Any performance improvements in the parallelization of the revised simplex algorithm would be of great interest. Using GPU computing for solving largescale LPs is a great challenge due to the capabilities of GPU architectures.
Some related works have been proposed on the GPU parallelization for LPs. O’Leary and Jung [17] proposed a CPU-GPU implementation of the Interior Point Method for dense LPs. Their computational results on Netlib Set [18] showed that some speedup can be gained for large dense problems. Spampinato and Elster [19] presented a GPU-based implementation of the Revised Simplex Algorithm on GPU with NVIDIA CUBLAS [20] and NVIDIA LAPACK libraries [21]. Their implementation showed a maximum speedup of 2.5 on randomly generated LPs of at most 2000 variables and 2000 constraints. Bieling et al. [22] also proposed a parallel implementation of the Revised Simplex Algorithm on GPU. They compared their GPU-based implementation with GLPK solver and found a maximum speedup of 18 in single precision. Lalami et al. [23] proposed a parallel implementation of the standard Simplex on a CPU-GPU systems. Their computational results on randomly generated dense problems of at most 4000 variables and 4000 constraints showed a maximum speedup of 12.5. Meyer et al. [24] proposed a mono and a multi-GPU implementation of the standard Simplex algorithm and compared their implementation with the CLP solver. Their implementation outperformed CLP solver on large sparse LPs. Li et al. [25] presented a GPU-based parallel algorithm, based on Gaussian elimination, for large scale LPs that outperform the CPU-based algorithm.
This paper presents a computational study in which the basis inverse is computed with five different updating schemes: 1) Gaussian elimination; 2) the built-in function inv of MATLAB; 3) LU decomposition; 4) product form of the inverse; and 5) a modification of the product form of the inverse; and incorporates them with the revised simplex algorithm. Then, we propose a parallel implementation of PFI and MPFI schemes, which were the fastest among the five updating methods, on a CPU-GPU System, which is based on MATLAB and CUDA.
The structure of the paper is as follows. In Section 2, a brief description of the revised simplex algorithm is presented. In Section 3, five methods that have been widely used for basis inversion are presented and analyzed. Section 4 presents the computational comparison of the serial implementations of the updating schemes. Computational tests were carried out on randomly generated LPs of at most 5000 variables and 5000 constraints. Section 5 presents the GPU-based implementations of two updating schemes. In Section 6, a computational study of the GPU-based implementations is performed. Finally, the conclusions of this paper are outlined in Section 7.
2. Revised Simplex Method
Using a partition (B, N) Equation (1) can be written as shown in Equation (3):
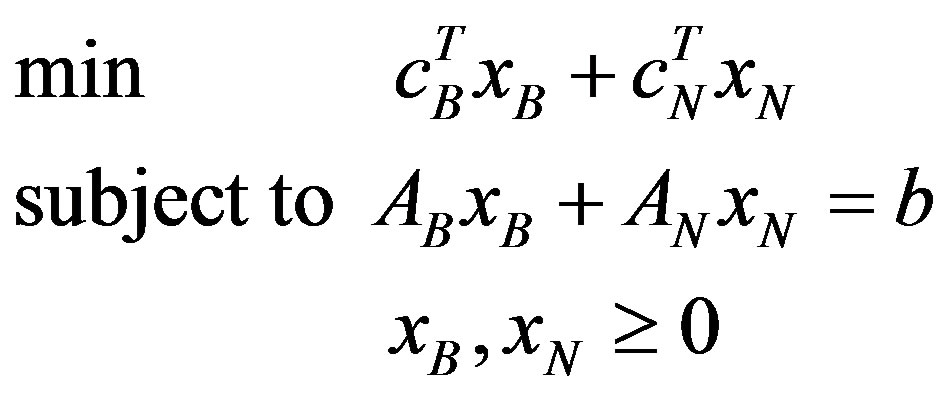 (3)
(3)
In the above problem, AB is an mxm non-singular submatrix of A, called basic matrix or basis. The columns of A belonging to subset B are called basic and those belonging to N are called non-basic. The solution of the linear problem 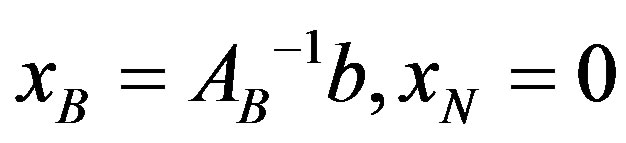 is called a basic solution. A solution
is called a basic solution. A solution 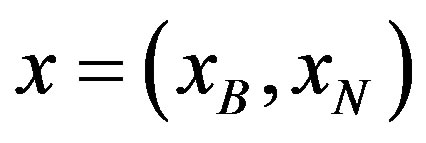 is feasible iff
is feasible iff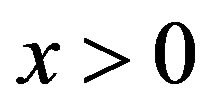 ; otherwise the solution is infeasible. The solution of the linear problem in Equation (2) is computed by the relation
; otherwise the solution is infeasible. The solution of the linear problem in Equation (2) is computed by the relation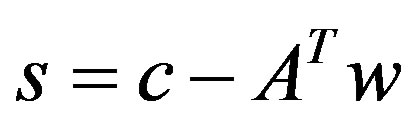 , where
, where 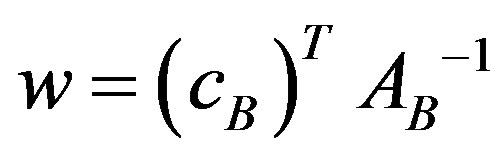 are the simplex multipliers and s are the dual slack variables. The basis AB is dual feasible iff
are the simplex multipliers and s are the dual slack variables. The basis AB is dual feasible iff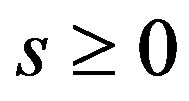 .
.
In each iteration, simplex algorithm interchanges a column of matrix AB with a column of matrix AN and constructs a new basis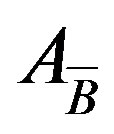 . Any iteration of simplex type algorithms is relatively expensive. The total work of an iteration of simplex type algorithms is dictated by the computation of the basis inverse. This inverse, however, does not have to be computed from scratch during each iteration of the simplex algorithm. Simplex type algorithms maintain a factorization of basis and update this factorization in each iteration. There are several schemes for updating basis inverse. In Section 3, we present eight well-known methods for the basis inverse. A formal description of the revised simplex algorithm [26] is presented in Table 1.
. Any iteration of simplex type algorithms is relatively expensive. The total work of an iteration of simplex type algorithms is dictated by the computation of the basis inverse. This inverse, however, does not have to be computed from scratch during each iteration of the simplex algorithm. Simplex type algorithms maintain a factorization of basis and update this factorization in each iteration. There are several schemes for updating basis inverse. In Section 3, we present eight well-known methods for the basis inverse. A formal description of the revised simplex algorithm [26] is presented in Table 1.
3. Basis Inversion Updating Schemes
3.1. Gaussian Elimination
Gaussian elimination is a method for solving systems of linear equations, which can be used to compute the inverse of a matrix. Gaussian elimination performs the

Table 1. Revised simplex algorithm.
following two steps: 1) Forward Elimination: reduces the given matrix to a triangular or echelon form and 2) Back Substitution: finds the solution of the given system. Gaussian elimination with partial pivoting requires O(n3) time complexity.
Gaussian elimination has been implemented on MATLAB using the mldivide operator. In order to find the new basis inverse using Gaussian elimination, one can use the Equation (5):
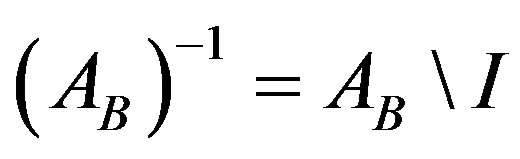 (5)
(5)
3.2. Built-In Function Inv of MATLAB
The basis inverse can be computed using the built-in function of MATLAB called inv, which uses LAPACK routines to compute the basis inverse. Due to the fact that this function is already compiled and optimized for MATLAB, its execution time is smaller compared with the other relevant methods that compute the explicit basis inverse; time-complexity, though, remains O(n3).
3.3. LU Decomposition
LU decomposition method factorizes a matrix as the product of an upper U and a lower L triangular factors, which can be used to compute the inverse of a matrix. In order to compute the U and L factors, the built-in function of MATLAB called lu has been used. LU decomposition can be computed in time O(n3).
3.4. MPFI
MPFI updating scheme has been presented by Benhamadou [3]. The main idea of this method is that the current basis inverse 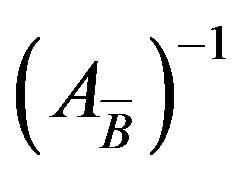 can be computed from the previous inverse
can be computed from the previous inverse 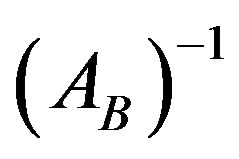 using a simple outer product of two vectors and one matrix addition, as shown in the Equation (6):
using a simple outer product of two vectors and one matrix addition, as shown in the Equation (6):
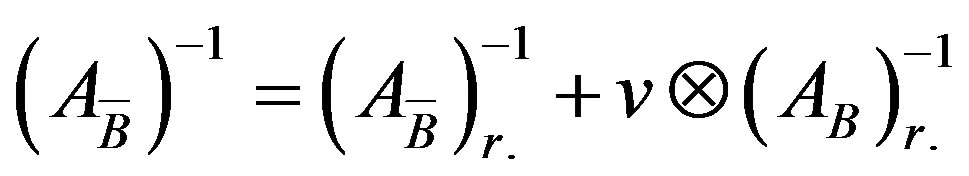 (6)
(6)
The updating scheme of the inverse is shown in Equation (7).
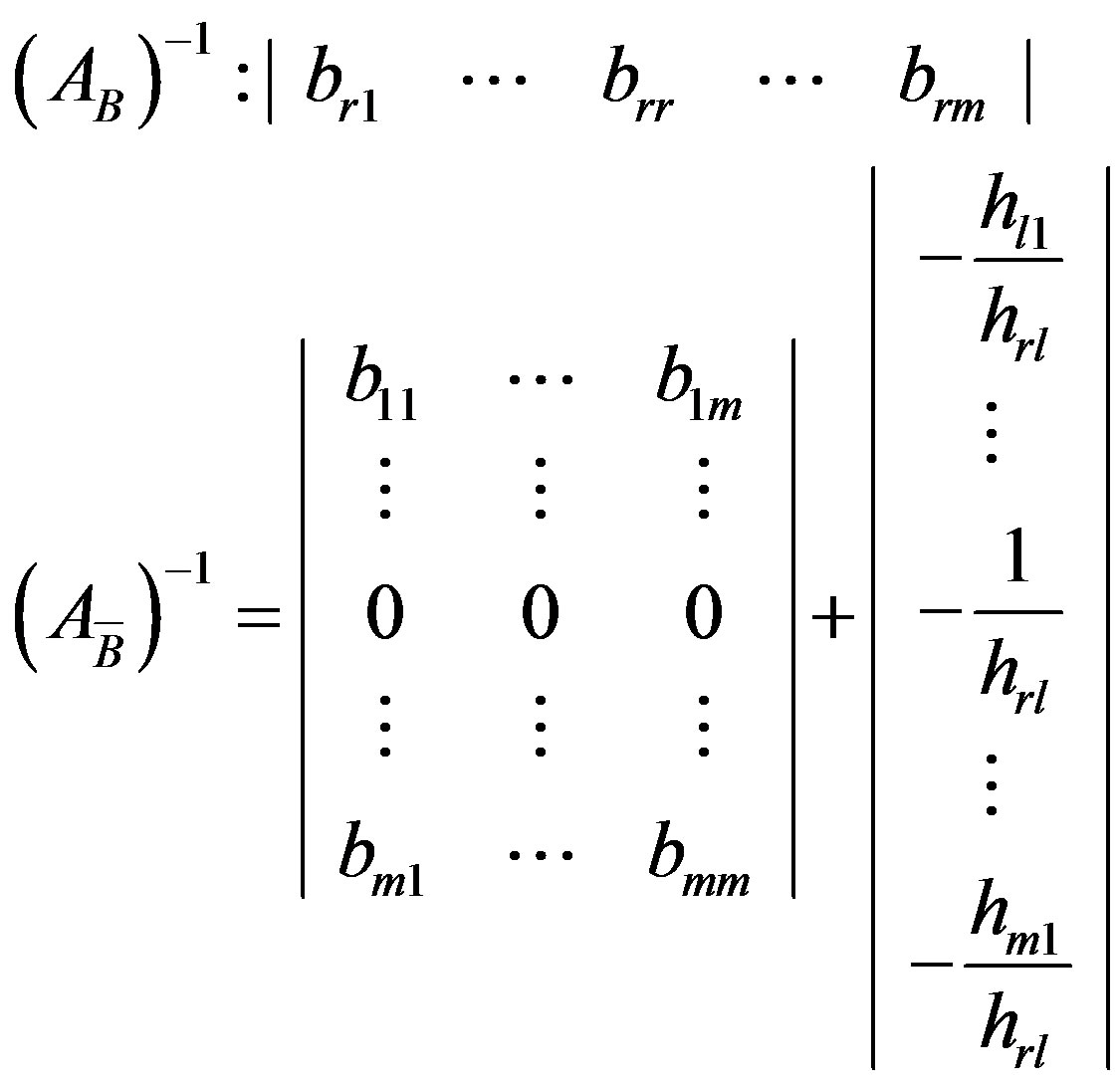 (7)
(7)
The outer product of Equation (7) requires m2 multiplications and the addition of two matrices requires m2 additions. Hence, the complexity is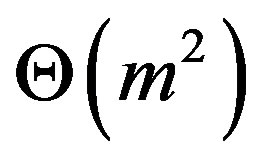 .
.
3.5. PFI
The PFI scheme, in order to update the new basis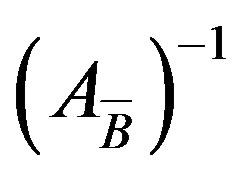 , uses information only about the entering and leaving variables along with the current basis
, uses information only about the entering and leaving variables along with the current basis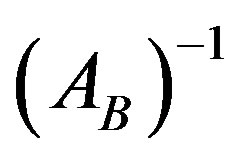 . The new basis inverse can be updated at any iteration using the Equation (8).
. The new basis inverse can be updated at any iteration using the Equation (8).
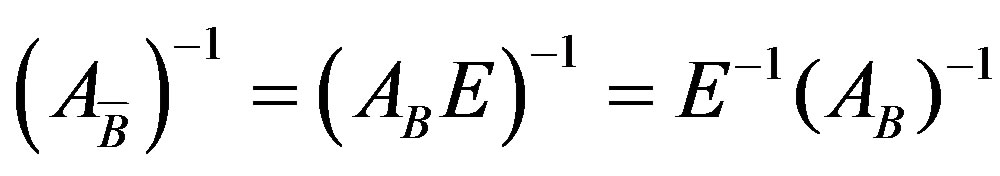 (8)
(8)
where E−1 is the inverse of the eta-matrix and can be computed by the Equation (9):
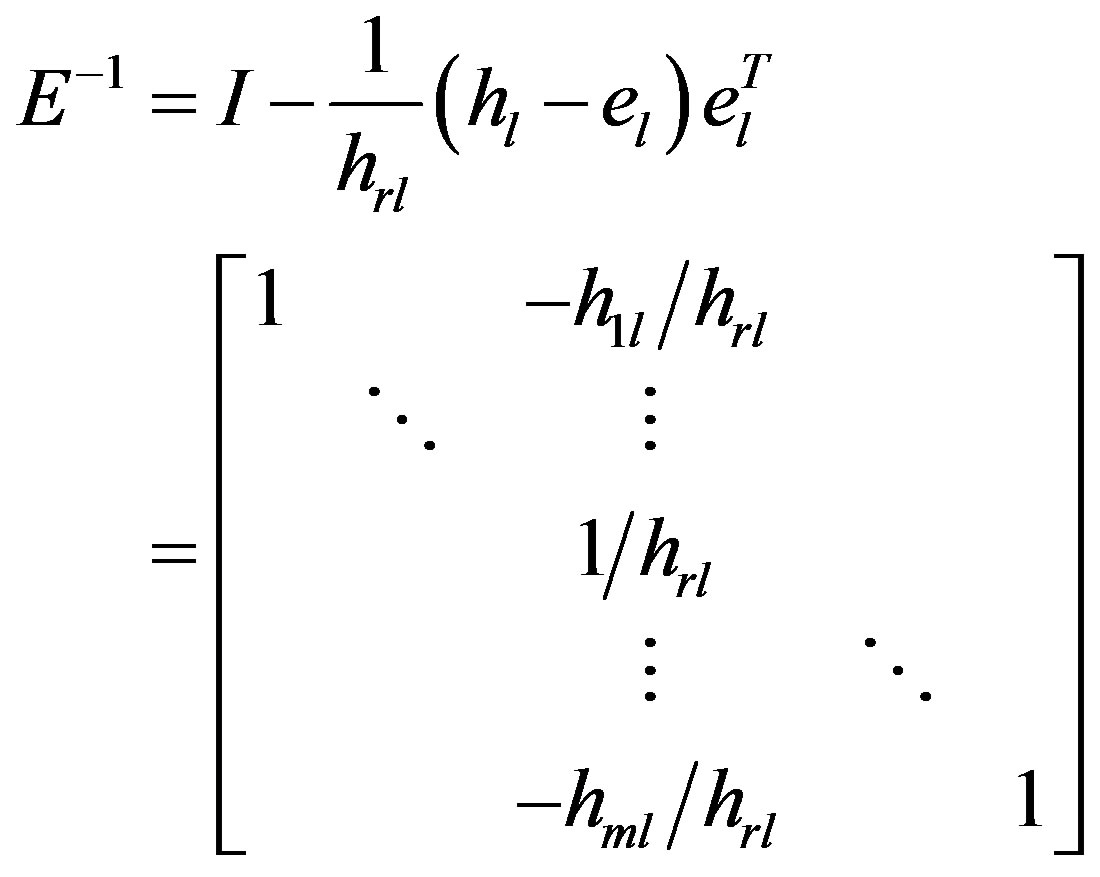 (9)
(9)
If the current basis inverse is computed using regular multiplication, then the complexity of the PFI is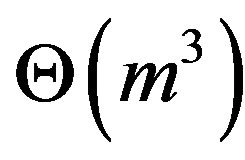 .
.
4. Computational Results of Serial Implementations
Computational studies have been widely used, in order to examine the practical efficiency of an algorithm or even compare algorithms. The computational comparison of the aforementioned five updating schemes has been performed on a quad-processor Intel Core i7 3.4 GHz with 32 Gbyte of main memory running under Microsoft Windows 7 64-bit. The algorithms have been implemented using MATLAB Professional R2012a. MATLAB (MATrix LABoratory) is a powerful programming environment and is especially designed for matrix computations in general. All times in the following tables are measured in seconds.
The test set used in the computational study was randomly generated. Problem instances have the same number of constraints and variables. The largest problem tested has 5000 constraints and 5000 variables. All instances are dense. For each instance, we averaged times over 10 runs. A time limit of 20 hours was set that explains why there are no measurements for some updating methods on large instances. It should be noted that in MATLAB R2012a multithreading is enabled by default thus our implementations are automatically parallelized and executed using the available multicore CPU.
Table 2 presents the results from the execution of the above mentioned updating schemes. We have also included the execution time from MATLAB’s linprog built-in function, a function for solving linear programming problems. MATLAB’s linprog function includes two algorithms for large-scale and medium-scale optimization. The large-scale algorithm is based on Interior Point Solver [27], a primal-dual interior-point algorithm. LIPSOL used a Cholesky-infinity factorization that causes overhead during the factorization of dense matrices and as a result it cannot solve problems with more than 1500 variables and constraints. Due to this restriction, we have used in our comparison the medium-scale algorithm, which is a variation of the simplex method. Table 3 includes the execution time for the basis inverse of each updating scheme, while Table 2 presents the total execution time. The execution time of the basis inverse and the whole algorithm for each updating scheme is also graphically illustrated in Figures 1 and 2, respectively.
The MPFI updating scheme has the best performance. On the other hand, LU updating method has the worst performance. Another significant issue is the performance of Gaussian elimination, PFI, function inv and linprog of MATLAB which are close to each other and the results are not quite satisfactory.
5. Parallel Implementation of PFI and MPFI Updating Schemes on a CPU-GPU System
PFI and MPFI were the fastest updating schemes. In this section, we present the GPU-based implementations of these updating methods taking advantage of the power that modern GPUs offer. The parallel implementations of these updating methods are implemented on MATLAB and CUDA. The updating methods are built using both native MATLAB code and CUDA MEX files.
Both methods take as input the previous basis inverse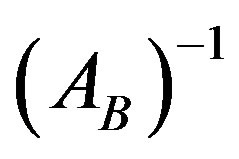 , the pivot column hl, the index of the leaving variable (k) and the number of the constraints (m).
, the pivot column hl, the index of the leaving variable (k) and the number of the constraints (m).
5.1. GPU-Based MPFI
Let us assume that we have t gpu cores. Table 4 shows the steps that we used to compute the new basis inverse
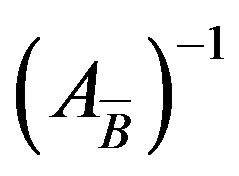 with the MPFI scheme on the GPU.
with the MPFI scheme on the GPU.
5.2. GPU-Based PFI
Table 5 shows the steps that we used to compute the new basis inverse 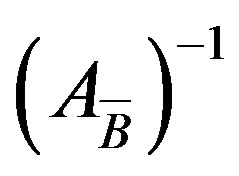 with the PFI scheme on the GPU.
with the PFI scheme on the GPU.
6. Computational Results of Parallel Implementations
The same randomly generated test set is also used in
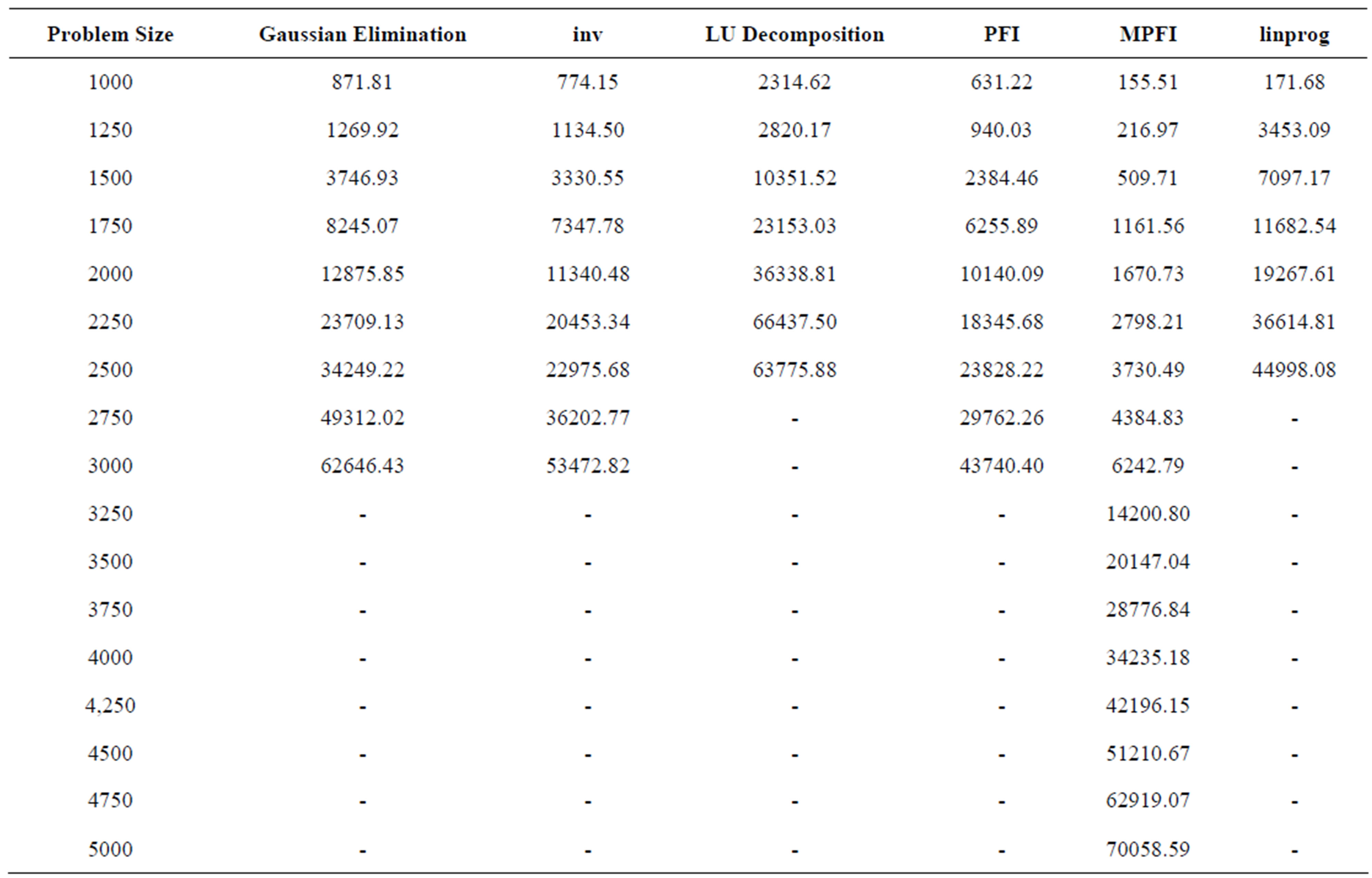
Table 2. Total time (secs).
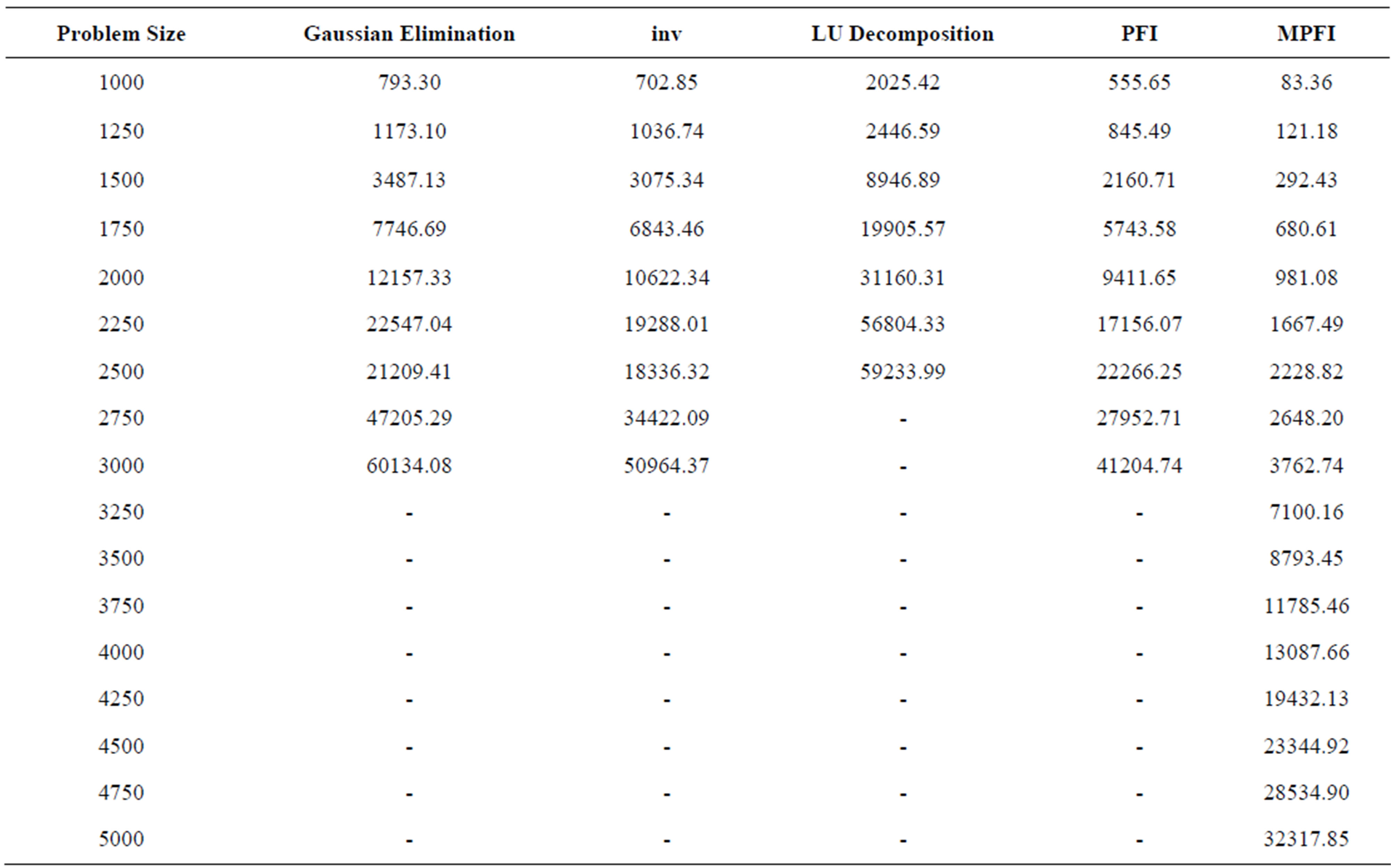
Table 3. Basis inverse time (secs).
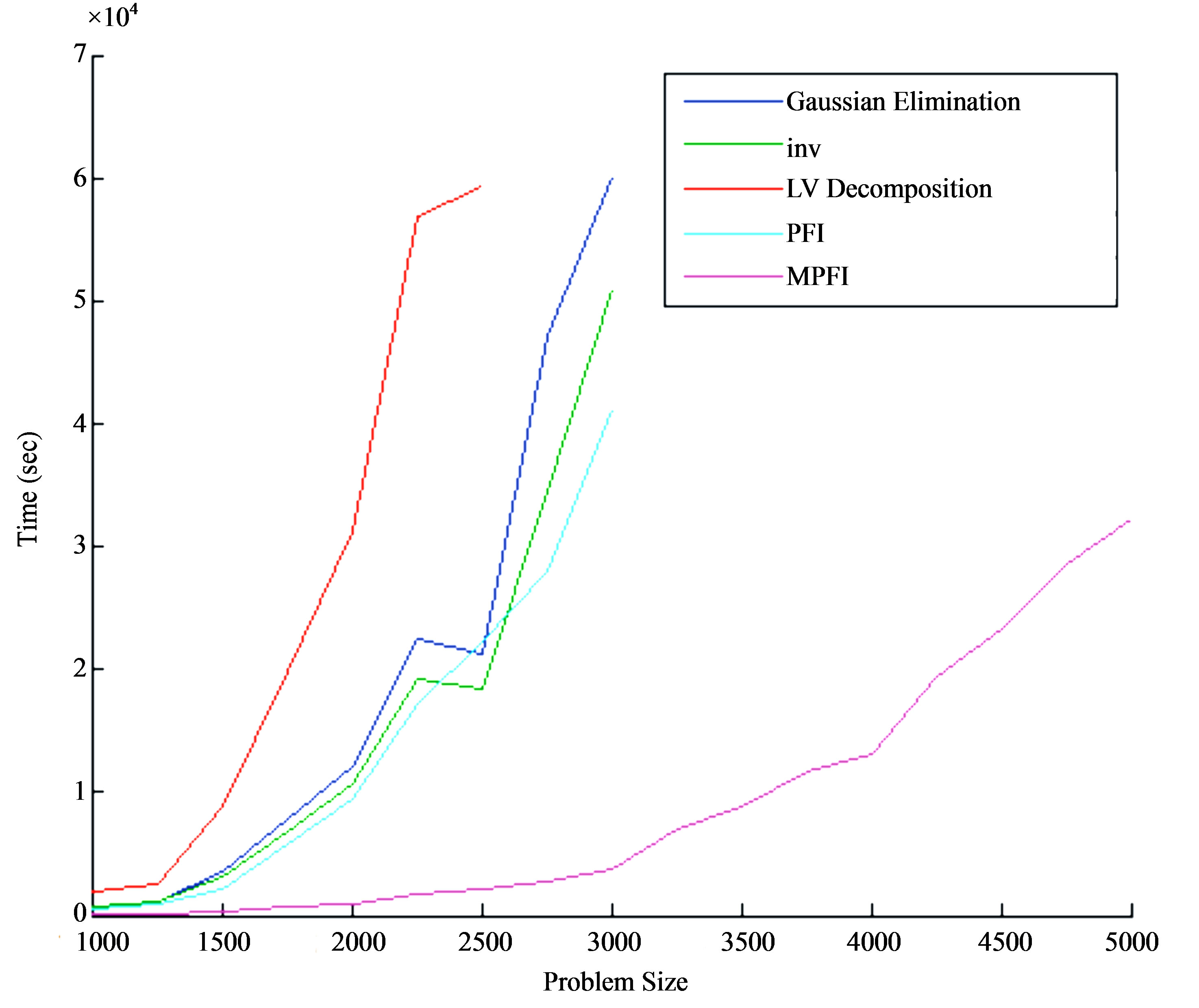
Figure 1. Basis inverse time comparison.
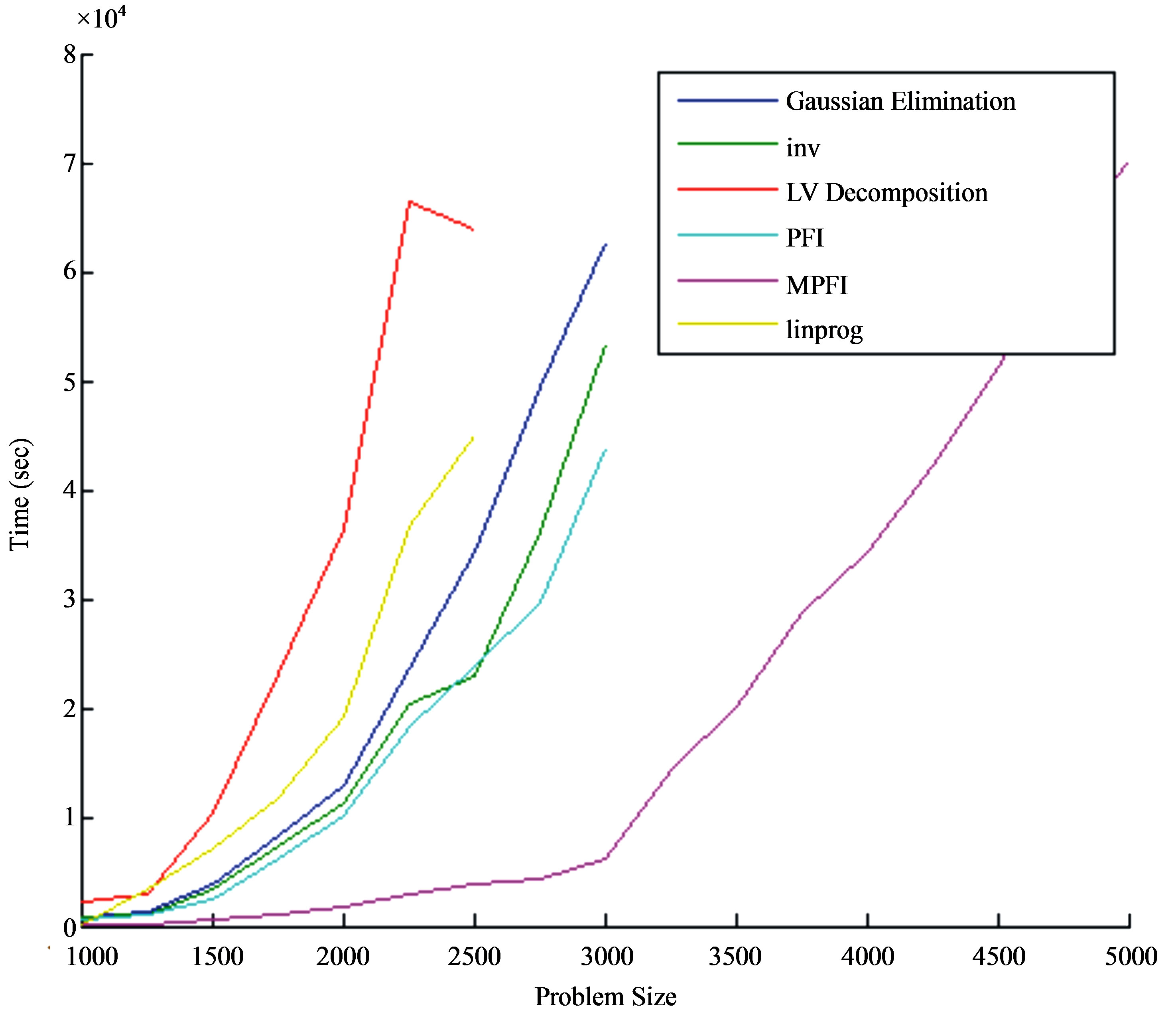
Figure 2. Total time comparison.
order to test the performance of the GPU-based implementations. The computational comparison of the parallel implementations has been also performed on a quadprocessor Intel Core i7 3.4 GHz with 32 Gbyte of main memory running under Microsoft Windows 7 64-bit and NVIDIA Quadro 6000 with 6 Gbyte of memory and 448 CUDA cores. The mex files have been implemented using CUDA 4.2 and Microsoft Visual Studio 2012. Table 6 presents the results from the execution of the GPUbased implementations of PFI and MPFI updating schemes. For each implementation, the table shows the CPU time for the basis inverse and the total time.
Table 7 presents the speedup obtained by the GPUbased implementations regarding the CPU time for the basis inverse and the total time. We now plot the ratios taken from Table 7 in Figure 3. The total time is in logarithmic scale.
From the results, we observe: 1) the MPFI scheme is much faster than PFI both in serial and in GPU-based implementation, 2) using PFI scheme, the speedup gained from the GPU implementation is around 7 for the time of basis inverse and 5.5 for total time when the

Table 4. GPU-based MPFI.

Table 5. GPU-based PFI.
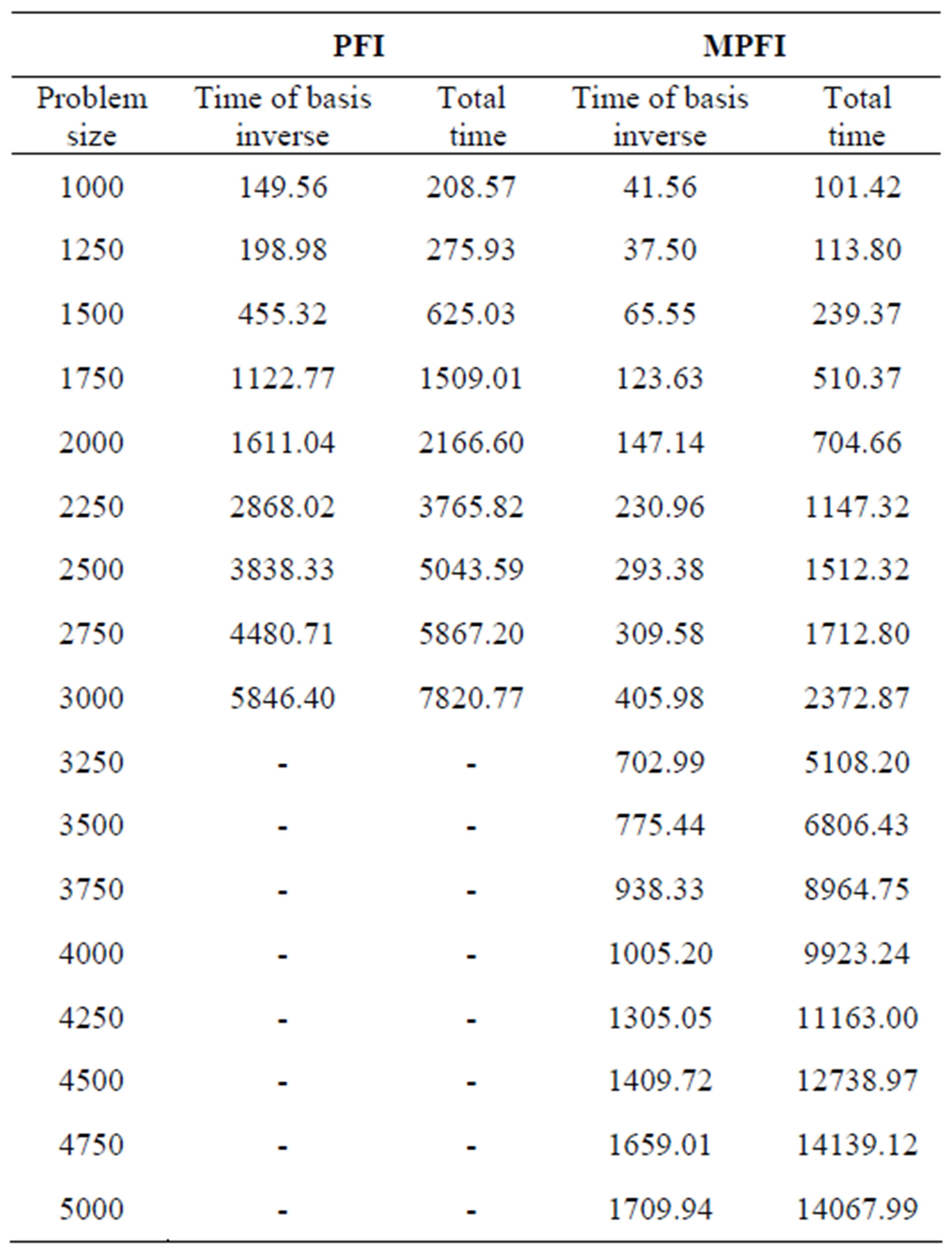
Table 6. Basis inverse and total time of the GPU-based implementations (secs).
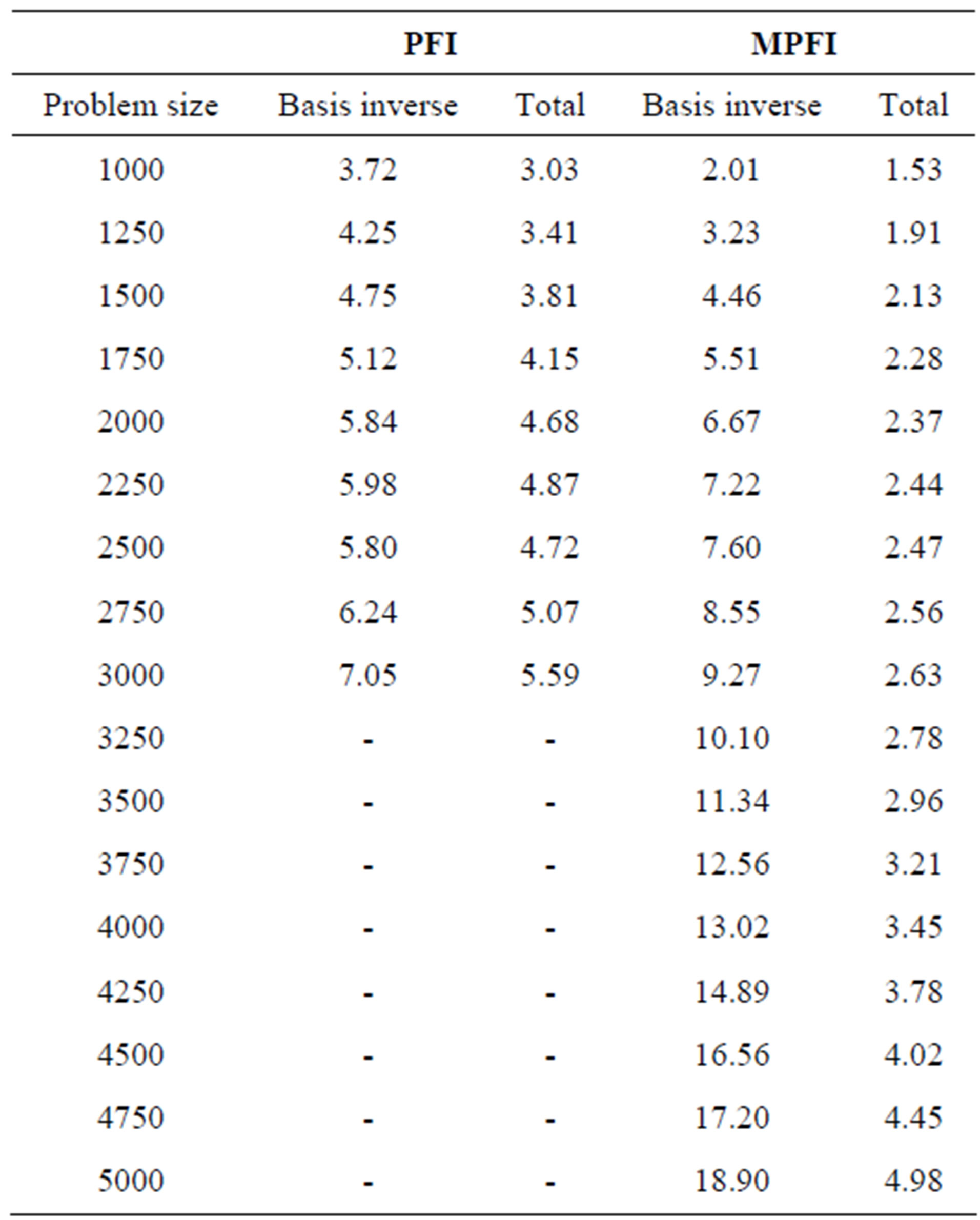
Table 7. Speedup obtained by the GPU-based implementations.
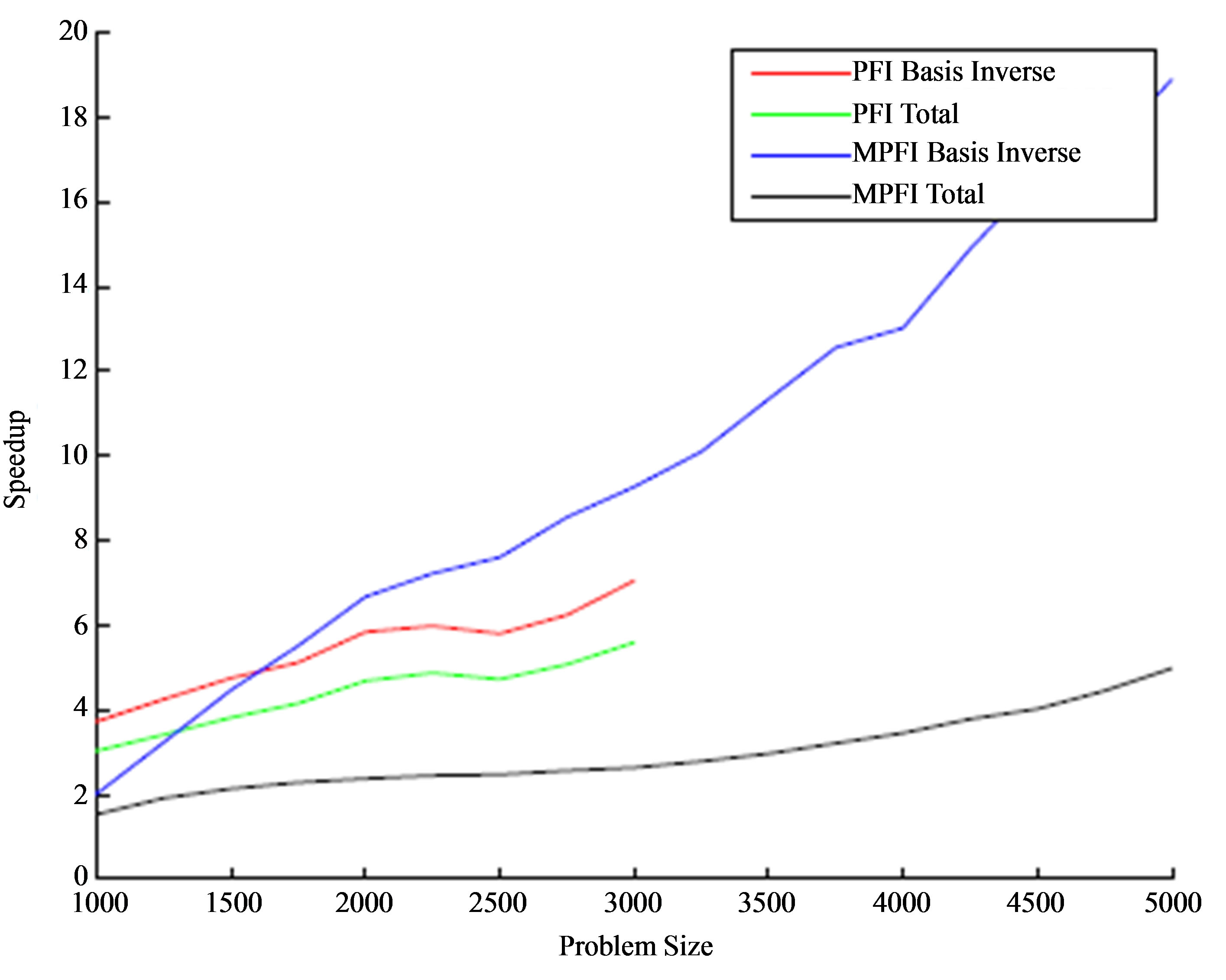
Figure 3. Speedup comparison.
problem size reaches to 3000 × 3000, and 3) using MPFI scheme, the speedup gained from the GPU implementation is around 19 for the time of basis inverse and 5 for total time when the problem size reaches to 5000 × 5000.
7. Conclusions
The basis inverse is the most time-consuming step in simplex type algorithms, so it is essential to implement a fast and numerically stable updating method. In this paper, we performed a computational comparison of five updating schemes and incorporated them to the revised simplex algorithm. The results of the computational study showed that MPFI updating scheme is the fastest when solving large dense LPs.
We proposed a GPU-based implementation for PFI and MPFI updating schemes, which were the fastest serial implementations, and implemented on MATLAB and CUDA. We performed again a computational study and found that GPU-based implementations of PFI and MPFI outperform the serial ones. More specifically, the speedup for PFI method is up to 7 for the time of basis inverse and 5.5 for the total time and the speedup for MPFI method is up to 19 for the time of basis inverse and 5 for total time. Our approach allows us to solve problems of size 10000 × 10000.
In future work, we plan to implement all the steps of the algorithm in order to fully parallelize the revised simplex method for GPUs. Moreover, we also plan to test sparse LPs and also port our application to a multi-GPU architecture.
8. Acknowledgements
The authors thank NVIDIA for support through their Academic Partnership Program.
REFERENCES
- G. B. Dantzig and W. Orchard-Hays, “The Product Form of the Inverse in the Simplex Method,” Mathematics of Computation, Vol. 8, 1954, pp. 64-67. http://dx.doi.org/10.1090/S0025-5718-1954-0061469-8
- M. Benhamadou, “On the Simplex Algorithm ‘Revised Form’,” Advances in Engineering Software, Vol. 33, No. 11, 2002, pp. 769-777. http://dx.doi.org/10.1016/S0965-9978(02)00037-6
- R. K. Brayton, F. G. Gustavson and R. A. Willoughby, “Some Results on Sparse Matrices,” Mathematics of Computation, Vol. 24, No. 115, 1970, pp. 937-954. http://dx.doi.org/10.1090/S0025-5718-1970-0275643-8
- H. Markowitz, “The Elimination Form of the Inverse and Its Applications to Linear Programming,” Management Science, Vol. 3, No. 3, 1957, pp. 255-269. http://dx.doi.org/10.1287/mnsc.3.3.255
- R. H. Bartels and G. H. Golub, “The Simplex Method of Linear Programming Using LU Decomposition,” Communications of the ACM, Vol. 12, No. 5, 1969, pp. 266- 268.
- J. J. H. Forrest and J. A. Tomlin, “Updated Triangular Factors of the Basis to Maintain Sparsity in the Product Form Simplex Method,” Mathematical Programming, Vol. 2, No. 1, 1972, pp. 263-278. http://dx.doi.org/10.1007/BF01584548
- J. Reid, “A Sparsity-Exploiting Variant of the BartelsGolub Decomposition for Linear Programming Bases,” Mathematical Programming, Vol. 24, No. 1, 1982, pp. 55-69. http://dx.doi.org/10.1007/BF01585094
- L. M. Suhl and U. H. Suhl, “A Fast LU Update for Linear Programming,” Annals of Operations Research, Vol. 43, No. 1, 1993, pp. 33-47. http://dx.doi.org/10.1007/BF02025534
- M. Saunders, “A Fast and Stable Implementation of the Simplex Method Using Bartels-Golub Updating,” In: J. Bunch and S. T. Rachev, Eds., Sparse Matrix Computation, Academic Press, New York, 1976, pp. 213-226.
- D. Goldfarb, “On the Bartels-Golub Decomposition for Linear Programming Bases,” Mathematical Programming, Vol. 13, No. 1, 1977, pp. 272-279. http://dx.doi.org/10.1007/BF01584343
- J. L. Nazareth, “Computer Solution of Linear Programs,” Oxford University Press, Oxford, 1987.
- V. Chvatal, “Linear Programming,” W. H. Freeman and Company, New York, 1983.
- P. F. McCoy and J. A. Tomlin, “Some Experiments on the Accuracy of Three Methods of Updating the Inverse in the Simplex Method,” Technical Report, Stanford University, Stanford, 1974.
- S. Lim, G. Kim and S. Park, “A Comparative Study between Various LU Update Methods in the Simplex Method,” Journal of the Military Operations Research Society of Korea, Vol. 29, No. 1, 2003, pp. 28-42.
- E. S. Badr, K. Paparrizos, N. Samaras and A. Sifaleras, “On the Basis Inverse of the Exterior Point Simplex Algorithm,” Proceedings of the 17th National Conference of Hellenic Operational Research Society (HELORS), Rio, 16-18 June 2005, pp. 677-687.
- N. Ploskas, N. Samaras and K. Margaritis, “A Parallel Implementation of the Revised Simplex Algorithm Using OpenMP: Some Preliminary Results,” Optimization Theory, Decision Making, and Operational Research Applications, Springer Proceedings in Mathematics & Statistics, Vol. 31, 2013, pp. 163-175. http://dx.doi.org/10.1007/978-1-4614-5134-1_11
- D. P. O’Leary and J. H. Jung, “Implementing an Interior Point Method for Linear Programs on a CPU-GPU System,” Electronic Transactions on Numerical Analysis, Vol. 28, 2008, pp. 879-899.
- D. M. Gay, “Electronic Mail Distribution of Linear Programming Test Problems,” Mathematical Programming Society COAL Newsletter, Vol. 13, 1985, pp. 10-12.
- D. G. Spampinato and A. C. Elster, “Linear Optimization on Modern GPUs,” Proceedings of the 23rd IEEE International Parallel and Distributed Processing Symposium, Rome, 25-29 May 2009, pp. 1-8.
- CUDA-CUBLAS Library 2.0, NVIDIA Corp., 2013. http://developer.nvidia.com/object/cuda.html
- LAPACK Library, 2013. http://www.cudatools.com
- J. Bieling, P. Peschlow and P. Martini, “An Efficient GPU Implementation of the Revised Simplex Method,” Proceedings of the 24th IEEE International Parallel and Distributed Processing Symposium, 19-23 April 2010, Atlanta, pp. 1-8.
- M. E. Lalami, V. Boyer and D. El-Baz, “Efficient Implementation of the Simplex Method on a CPU-GPU System,” Proceedings of the 2011 IEEE International Symposium on Parallel and Distributed Processing Workshops and PhD Forum, Washington DC, 16-20 May 2011, pp. 1999-2006.
- X. Meyer, P. Albuquerque and B. Chopard, “A MultiGPU Implementation and Performance Model for the Standard Simplex Method,” Proceedings of the 1st International Symposium and 10th Balkan Conference on Operational Research, Thessaloniki, 22-25 September 2011, pp. 312-319.
- J. Li, R. Lv, X. Hu and Z. Jiang, “A GPU-Based Parallel Algorithm for Large Scale Linear Programming Problem,” In: J. Watada, G. Phillips-Wren, L. Jai and R. J. Howlett, Eds., Intelligent Decision Technologies, SIST 10, Springer Berlin Heidelberg, Springer-Verlag, Berlin, 2011, pp. 37-46. http://dx.doi.org/10.1007/978-3-642-22194-1_4
- G. B. Dantzig, A. Orden and P. Wolfe, “The Generalized Simplex Method,” RAND P-392-1, RAND Corporation, 1953.
- Y. Zhang, “Solving Large-Scale Linear Programs by Interior-Point Methods Under the MATLAB Environment,” Technical Report TR96-01, Department of Mathematics and Statistics, University of Maryland, Baltimore, 1995.
NOTES
*Corresponding author.

