American Journal of Operations Research
Vol.3 No.3(2013), Article ID:31677,11 pages DOI:10.4236/ajor.2013.33034
Tour Planning for Sightseeing with Time-Dependent Satisfactions of Activities and Traveling Times
1Graduate School of Information Science and Technology, Osaka Univeristy, Osaka, Japan
2Graduate School of Engineering, Hiroshima Univeristy, Hiroshima, Japan
3Multidimensional Data Analysis Group, Department of Data Science, The Institute of Statistical Science, Tokyo, Japan
4Department of Mathematical Sciences, Faculty of Science and Engineering, Doshisha University, Kyoto, Japan
Email: thasuike@ist.osaka-u.ac.jp, katagiri-h@hiroshima-u.ac.jp, tsubaki@ism.ac.jp, htsuda@mail.doshisha.ac.jp
Copyright © 2013 Takashi Hasuike et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 11, 2013; revised April 15, 2013; accepted April 27, 2013
Keywords: Tour Planning Problem; Time-Dependent Parameters; Time-Expanded Network; Mathematical Modeling
ABSTRACT
This paper proposes a new personal tour planning problem with time-dependent satisfactions, traveling and activity duration times for sightseeing. It is difficult to represent the time-dependent model using general static network models, and hence, Time-Expanded Network (TEN) is introduced. The TEN contains a copy to the set of nodes in the underlying static network for each discrete time step, and it turns the problem of determining an optimal flow over time into a classical static network flow problem. Using the proposed TEN-based model, it is possible not only to construct various variations with time of costs and satisfactions flexibly in a single network, but also to select optimal departure places and accommodations according to the tour route with tourist’s favorite places and to obtain the time scheduling of tour route, simultaneously. The proposed model is formulated as a 0 - 1 integer programming problem which can be applied by existing useful combinatorial optimization and soft computing algorithms. It’s also equivalently transformed into several existing tour planning problems using some natural assumptions. Furthermore, comparing the proposed model with some previous models using a numerical example with time-dependent parameters, both the similarity of these models in the static network and the advantage of the proposed TEN-based model are obtained.
1. Introduction
The rapid development of information communication and technologies (ICT), specifically internet technologies, enables tourists to use the vast amount of information available on the Web and to construct their personal tour planning for sightseeing by themselves. Therefore, it is important to develop a decision support system for the tour planning to suit personal satisfactions under various budget and time constraints. The tour planning is a multimodal and complex constructive activity affected by various factors, which can be classified into the following two categories (Zhu et al. [1]): 1) personal features including both socioeconomic factors (for instance, age, education, and income) and psychological and cognitive factors (for instance, experience, personality, and involvement); and 2) travel features such as travel purpose, number of travelers, length of travel, distance, and transportation mode. Furthermore, tourists should specially consider traveling and activity times, and hence, it is important to do a suitable management of these times for the effective utilization of sightseeing activities. Thus, the tour planning should be prepared in advance, considering the above-mentioned factors and parameters such as transportation networks, personal context, properties of activities, and traveling and activity times.
Previous researches on the tour planning problem are broadly classified into several groups; for instance, solving the problem from a mathematical point of view, dynamically planning an optimal itinerary which is related to finding a path, designing intelligent tour planning systems based on the personalized tour recommender, etc. (in detail, see Abbaspour and Samadzadegan [2]). Specifically, in this paper, we focus on the group formulating and solving a new tour planning problem with time-dependent parameters from a mathematical point of view. As recent studies of the tour planning problems, Souffriau et al. [3] solved the tourist trip design problem, in addition to tour planning, they developed an approach to extract the scores associated with valuable points of interest automatically. Zografos and Androutsopoulos [4] formulated a tour planning problem in a multimodal and time-scheduled urban public transport network, lexicographically optimizing the en-route time, the number of transfers, and the total walking and waiting time. Then, they developed a dynamic programming-based algorithm for determining the lexicographically optimal tour route. Zhu et al. [1] established a framework for the more general tour planning problem, which also considers the selection of accommodation, as an integer linear programming problem in terms of mathematical programming, and developed heuristic algorithms. Abbaspour and Samadzadegan [2] developed a time-dependent tour planning methodology to design a time-limited tour that collects the maximum total priority value. As the other researches related to tour planning for sightseeing, there are recently various studies of traveling time prediction and psychological aspect of sightseeing (for instance, Bohte and Maat [5], Ettema et al. [6], Hu et al. [7], Khosravi et al. [8]).
However, these existing mathematical models do not include several important factors for the tour planning such as time-dependent satisfaction values of activities and required traveling times between two places. For instance, from the traffic data, we may estimate the delay time in the case of traffic jam. The traffic jam tends to happen on the specific or particular time and road such as the rush hour and the main street, and hence, it is important to consider the time-dependent initially in the given network. Furthermore, with respect to sightseeing spots such as zoos, aqua museums, and theaters, some entertainments are performed in particular hours, for instance between 1:00 p.m. to 3:00 p.m. Therefore, satisfactions of tourists in only the particular hours may be the highest of the other hours. In addition, many previous models considered that the starting and terminal points such as stations and hotels are initially fixed, and the tourist decided the tour planning between these two fixed points. However, in actuality, there are some places which the tourist would like to visit certainly or absolutely, and so the starting and terminal points should be determined according to locations of these specific places. In order to overcome these drawbacks and to construct the more general framework of tour planning, we develop a new mathematical model of tour planning with time-dependent satisfactions considering the decision of not only optimal tour routes but also departure points and accommodation maximizing the total satisfaction of tourist.
As the above-mentioned, it is important to consider the time-dependent parameters in the tour planning problems as well as network optimization such as maximum flow problems (for instance, Cai et al. [9]). However, it is generally hard to represent these necessary conditions to deal with time-dependent parameters using only the static network structure, because static network optimization problems give only one deterministic value to each edge not to depend on clock times. Therefore, in order to deal with time-dependent parameters, we introduce a network structure called Time-Expanded Network (TEN), which is sometimes known as Time Space Network (TSN). The TEN contains a copy to the set of nodes in the underlying static network for each discrete time step. The advantage of this approach is that it turns the problem of determineing an optimal flow over time into a classical static network flow problem on the TEN. Therefore, using the advantage, many researchers have considered applying the TEN to practical problems since the 1970s and 1980s (for instance, Florian et al. [10], Zawack and Gerald [11]). In most recently, TEN-based models also have been proposed for various practical problems such as airline and crew scheduling (Engineer et al. [12], Guo et al. [13], Hane et al. [14]), multi-depot bus scheduling (Kliewer et al. [15]), optimal capacity utilizations for intelligent transportation management of traffic coordination systems (Shah et al. [16]), car pooling problems (Yan and Chen [17]), planning earth recycling and dump truck dispatching (Chu et al. [18]), etc. Then, Time-Expanded Decision Network (TDN) is also a method to clearly and rigorously represent feasible paths and, to the extent possible, quantify the expected switching costs along those paths. These paths and costs can then be represented on a directed network with arc-costs representing cost-elements incurred during system operation, and expanded through a life-cycle using standard methods from time-expanded network theory (Jarvis and Ratliff [19]). Once formulated, decision makers can use the TDN to conduct scenario planning and iteratively design more evolvable complex systems. Therefore, in this paper, we focus on the modeling of personal tour planning considering several factors for times and satisfactions, and apply these advantages and usefulness of TEN to our proposed tour planning problem. This is the first study to apply both time-dependent parameters and TEN to the tour planning problem.
This paper is organized as follows. In Section 2, we introduce the TEN and explain features of TEN. In Section 3, we introduce constraints and an object of our proposed model, and formulate our proposed personal tour planning using the TEN. Furthermore, assuming the initially deterministic departure point and accommodation, we show that the proposed model is equivalently transformed into a constrained network optimization problem, which is similar to several types of previous tour planning problem. In Section 4, we provide a numerical example and show features of our proposed model. Finally, in Section 5, we conclude this paper.
2. Time-Expanded Network
The TEN contains a copy to the set of nodes in the underlying static network for each discrete time step. The advantage of this approach is that it turns the problem of determining an optimal flow over time into a classical static network flow problem on the TEN. This problem can be solved by well-known network flow algorithms. The TEN-based methodology involves 1) identifying and quantifying switching values of parameters; 2) creating an optimization model based on the concept of TEN; and 3) solving the model under probabilistic or manually generated scenarios for parameters to identify optimal designs.
The methodology of TEN-based decision making generally consists of the following five steps introduced by Silver and Weck [20].
- Designing an initial set of feasible system configuretions
- Quantifying switching parameters and creating a static network
- Creating the time expanded network
- Create scenarios and run optimization
- Modifying system configurations: Iterative design In this paper, we construct the TEN as the following steps based on previous studies and above-mentioned steps of TEN.
2.1. Expansion of the Static Network
The first step of standard techniques constructing the TEN is to consider discrete steps of time and make a copy of the original static network for every time step from time zero to the time horizon T. For instance, considering the given static network in Figure 1, we create a copy to set of nodes for each time period as described in Figure 2.
The general tour planning problem is regarded as a discrete time model due to train and bus transportations running on schedule such as every 10 minutes, and so it is possible to formulate our proposed time-dependent model as the TEN-based network model, and to obtain an optimal set of nodes in feasible tour routes of the TEN by solving the proposed model using network optimization.

Figure 1. Example of static network.
2.2. Connecting Nodes with Directed Edges
The second step constructing our proposed TEN-based model is to connect nodes with directed edges according to the corresponding time durations. Figure 3 shows a part of TEN-based tour planning problem extending the static network in Figure 1. This example assumes that place 1 is the departure point of the tour. For instance, directed edge (a) represents that tourists can travel from place 1 at time 0 to place 2 at time t1 by taxi. On the other hand, directed edge (b) also represents the traveling time duration of place 1 at time 0 to place 2 time t2 by bus. This difference arises from the usage of different transportations. Furthermore, directed edges (c) and (d) represent the activity duration times of place 2 in different clock times. If we assume that place 2 is crowded after time t2, and it may take more active duration times than usual conditions.
Thus, using the TEN, we can deal with different traveling and activity time durations to the same route and activity in the static network.
2.3. Setting Satisfaction Values and Costs to Each Directed Edge
In a similar way to traveling and activity time durations, we can set different satisfaction values and costs (s, c) with respect to each directed edge for every time step. Figure 4 shows a part of our proposed model with satisfaction values and costs.
For instance, in previous subsection, we mentioned that the difference of traveling times to directed edges (a) and (b) arose from the usage of different transportations. According to this assumption, we set values of costs to edges (a) and (b) as Figure 4, because taking a bus is generally cheaper than a taxi. In addition, if we assume

Figure 4. A part of TEN for the tour planning model with satisfaction values and costs (s, c).
that place 2 is crowded after time t2, and it may take more active duration times than usual conditions. Therefore, the satisfaction value of (c) is larger than that of (d). Thus, using the network model obtained through these steps to construct TEN from the static network model, we propose and formulate a personal tour planning problem with time-dependent parameters.
3. Formulation of the Proposed Tour Planning Problem
In this paper, we propose a new tour planning problem to decide an optimal route maximizing the total satisfaction value of the tourist under time-dependent parameters. We assume that traveling times from a sightseeing point to the other points and activity duration times of each sightseeing point are dependent on clock times. Each satisfaction value is set according to the corresponding clock time in the above situations. Therefore, even if there is the same route between two sightseeing places in different two feasible routes, the traveling times are often different from each other according to clock times. Similarly, even if there is the same sightseeing place in different two feasible routes, activity duration times and satisfaction values are also different from each other according to clock times and crowded conditions. Thus, it is important to introduce these time-dependent parameters according to each clock time in the tour planning problem. We propose a more versatile tour planning problem to suit the personal tourist’s preference than existing models by introducing the idea of TEN introduced in Section 2.
3.1. Parameters in Our Proposed Model
Let  be a connected graph in TEN.
be a connected graph in TEN.  is the set of directed edges and
is the set of directed edges and  is the set of nodes mathematically defined as
is the set of nodes mathematically defined as  where each set is derived from the following conditions, respectively.
where each set is derived from the following conditions, respectively.
![]() : index set of departure candidate places
: index set of departure candidate places
 : index set of particular sightseeing places where the tourist certainly visits
: index set of particular sightseeing places where the tourist certainly visits
 : index set of same type of activity spots or sightseeing points such as restaurants and chain stores of souvenir. By grouping theses activity spots or sightseeing points, we can set K groups as
: index set of same type of activity spots or sightseeing points such as restaurants and chain stores of souvenir. By grouping theses activity spots or sightseeing points, we can set K groups as . The tourist must visit the only one place in each
. The tourist must visit the only one place in each 
 : index set of the other places except for place
: index set of the other places except for place

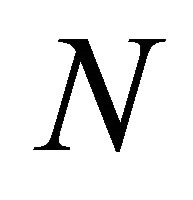 : index set of nodes for accommodations The our proposed TEN-based formulation to the tour planning problem is the more general and extended model than existing models, because one accommodation and start point can be selected in some accommodations and start points. The notation of parameters is as follows:
: index set of nodes for accommodations The our proposed TEN-based formulation to the tour planning problem is the more general and extended model than existing models, because one accommodation and start point can be selected in some accommodations and start points. The notation of parameters is as follows:
![]() : total tour time initially set by the tourist, which means the time horizon
: total tour time initially set by the tourist, which means the time horizon
 : time step satisfying
: time step satisfying 
where ![]() is the total step decided by the tourist
is the total step decided by the tourist
 : satisfaction values to obtain by traveling from site i at time t to site j at time
: satisfaction values to obtain by traveling from site i at time t to site j at time . Specifically, in the case of sightseeing of site i, satisfaction value
. Specifically, in the case of sightseeing of site i, satisfaction value  is assumed to be time-dependent parameters characterized by function
is assumed to be time-dependent parameters characterized by function . In this paper, we assume that all satisfaction values are initially set by tourist’s hobby and purpose, and the other tourists’ information on the Web using the Web intelligence analysis
. In this paper, we assume that all satisfaction values are initially set by tourist’s hobby and purpose, and the other tourists’ information on the Web using the Web intelligence analysis
 : costs to travel from site i at time t to site j at time
: costs to travel from site i at time t to site j at time 
 : minimum visiting points initially decided by the tourist
: minimum visiting points initially decided by the tourist
 : total budget available for the tour
: total budget available for the tour
 : 0 - 1 decision variables satisfying the following condition:
: 0 - 1 decision variables satisfying the following condition:

 : 0-1 decision variables satisfying the following condition:
: 0-1 decision variables satisfying the following condition:

3.2. Constraints in Our Proposed Model
TEN-based models are generally formulates as a network optimization problem, and hence, our proposed model includes the following constraints derived from network structures in mathematical programming.
1) Route construction constraint in network optimization:
If the tourist visit place j from the other sightseeing place at time , i.e.,
, i.e.,  , the tourist would leave this place to the next only one place p in the next time, i.e.,
, the tourist would leave this place to the next only one place p in the next time, i.e.,  , or do sightseeing this place, i.e.,
, or do sightseeing this place, i.e., . Therefore, this flow of tourist is mathematically formulated as follows in network optimization:
. Therefore, this flow of tourist is mathematically formulated as follows in network optimization:

For instance, consider the following part of TEN to the route planning problem as shown in Figure 5. In this case, we assume that all places 1 to R are included in
 . Figure 5 shows that a successive tour route from place 2 at time t* to place 3 at time t* + 1 and from place
. Figure 5 shows that a successive tour route from place 2 at time t* to place 3 at time t* + 1 and from place

Figure 5. Part of TEN for a route planning problem at from time t* to t* + 3.
3 at time t* + 1 to place 4 at time t* + 2 is constructed, i.e., ![]() , and the other decision variables
, and the other decision variables ![]() hold.
hold.
2) Departure point constraint:
The tourist starts sightseeing at time 0 from only one departure point i in candidate sites![]() , and goes to only one sightseeing place j at time
, and goes to only one sightseeing place j at time  in candidate places
in candidate places
 , i.e.,
, i.e., . Therefore, this constraint is represented as the following form:
. Therefore, this constraint is represented as the following form:

For instance, consider the following part of TEN as shown in Figure 6. In this case, we assume that all departure candidate points S1 to Sq are included in . Figure 6 shows that a tour route from departure candidate point S2 at time 0 to place 1 at time 2, i.e.,
. Figure 6 shows that a tour route from departure candidate point S2 at time 0 to place 1 at time 2, i.e.,  , and the other decision variables
, and the other decision variables
 holds.
holds.
3) Arrival point constraint:
In similarly, the tourist certainly arrives at only one accommodation i in candidate points  at time
at time  from only one sightseeing place j at time
from only one sightseeing place j at time  in candidate places
in candidate places , i.e.,
, i.e., . Thereforethis constraint is represented as follows:
. Thereforethis constraint is represented as follows:

For instance, consider the following part of TEN as shown in Figure 7. In this case, we assume that all departure candidate points N1 to ND are included in .
.

Figure 6. First part of TEN for a route planning problem at from time 0 to 3.

Figure 7. Final part of TEN for a route planning problem at from time 0 to te.
Figure 7 shows that a tour route from sightseeing place 2 at time  to arrival point N2 at time
to arrival point N2 at time![]() , i.e.,
, i.e.,
![]() , and the other decision variables
, and the other decision variables  holds.
holds.
4) Number of visiting places constraint:
From the notation of ,
,  means that the tourist does sightseeing at sightseeing place i from time t to t’. Since parameter b means minimum visiting points initially decided by the tourist, we formulate visiting places constraint as follows:
means that the tourist does sightseeing at sightseeing place i from time t to t’. Since parameter b means minimum visiting points initially decided by the tourist, we formulate visiting places constraint as follows:

For instance, consider the above Figure 5 to the route planning problem. Figure 5 shows that a tourist does sightseeing at place 4 from time t* + 2 to t* + 3 is constructed, i.e., ![]() holds.
holds.
5) Constraint to group :
:
As the above-mentioned parameter setting in subsection 3.1,  is the index set including particular sightseeing places where the tourist certainly visits, i.e., the tourist must visit this point only one time. This is formulated as follows:
is the index set including particular sightseeing places where the tourist certainly visits, i.e., the tourist must visit this point only one time. This is formulated as follows:

6) Constraint to groups :
:
As the above-mentioned parameter setting in subsection 3.1, each  is an index set of same type of activity spots or sightseeing points such as restaurants and chain stores of souvenir where the tourist is satisfied by going to only one places., i.e., the only one activity spot or sightseeing point is selected in the specific group
is an index set of same type of activity spots or sightseeing points such as restaurants and chain stores of souvenir where the tourist is satisfied by going to only one places., i.e., the only one activity spot or sightseeing point is selected in the specific group , and the tourist must visit this point only one time. This is formulated as follows:
, and the tourist must visit this point only one time. This is formulated as follows:

7) Constraint to group :
:
Contrary to constraints (5) and (6), the tourist can also visit sightseeing places which are grouped to  while there’s still traveling time, i.e., the tourist does not visit them if there is no traveling time. This situation is mathematically formulated as the following inequalities:
while there’s still traveling time, i.e., the tourist does not visit them if there is no traveling time. This situation is mathematically formulated as the following inequalities:

8) Cost constraint:
It takes some money costs to travel between two places and do sightseeing at a sightseeing place. Therefore, the cost constraint is introduced as follows:

where A is the connected graph with time-dependent parameters , and C is the target level of total cost set by the tourist.
, and C is the target level of total cost set by the tourist.
9) Constraint of 0-1 decision variable:
From the notation of parameters , if route
, if route  in TEN is included in the optimal route of our proposed model,
in TEN is included in the optimal route of our proposed model,  is equal to 1. If not,
is equal to 1. If not,  is equal to 0. Therefore, the following constraint is introduced:
is equal to 0. Therefore, the following constraint is introduced:

3.3. Objective Function and Formulation of Our Proposed Model
The object in this paper is maximizing the total satisfaction value of all sites visited by the tourist. The total satisfaction value is formulated as
 , and hence, our proposed model is formulated as the following TEN-based tour planning problem (TEN-TPP) maximizing the total tourist satisfaction:
, and hence, our proposed model is formulated as the following TEN-based tour planning problem (TEN-TPP) maximizing the total tourist satisfaction:

If we deal with this proposed tour planning problem applying time-dependent parameters to the coefficients simply and replacing edges according to the change of required time, we can decide not only the optimal tour route satisfying the tourist’s satisfaction but also appropriate time scheduling of the tour route, simultaneously. In Zhu et al. [1], the departure and arrival places in the obtained tour route should be the same. However, in our proposed model, we can set these places as different sets of nodes S and N according to tourist’s needs. Constraints (3) and (4) represent the above-mentioned situation. Therefore, the above proposed problem is the mathematical formulation to apply the TEN to the tour planning problem for the first time, and more general than Zhu’s model.
By solving our proposed model, the tourist obtains not only the optimal tour route with appropriate departure place and accommodation but also the time schedule, simultaneously. Furthermore, if the departure place s and accommodation n are initially determined, constraints (1) to (3) are organized as the following form:
 (10)
(10)
Therefore, our proposed model is equivalently transformed into the following problem:

This problem is similar to several types of previous tour planning problems, and so our proposed problem TEN-TPP is more general tour planning problem than the others. Furthermore, in this problem, constraint (10) is a standard constraint of general network flow, and so this problem is one of the constrained network optimization problems. Therefore, we may solve the problem using the network optimization method strictly or heuristic solution algorithm efficiently; branch-and-cut algorithm (Fischetti et al. [21]), 2-opt or n-opt algorithm (Chao et al. [22], Zhu et al. [1]), LP relaxation (Kennington and Nicholso [23]), Genetic algorithm (Abbaspour and Samadzadegan [2]), Neural network (Wang et al. [24]), Tabu-search (Gendreau et al. [25], Tang and Miller-Hooks [26]), Ant Colony Optimization (Ke et al. [27]), etc. Most recently, tabu search-based algorithms are widely used in various types of large-scale practical problems formulated as 0-1 programming problems, for instance, Job shop scheduling problem (Fattahi et al. [28]), Airport gate assignment problem (Seker and Noyan [29]), Service overlay network in the telecommunication system (Elias et al. [30]), etc. Therefore, we will solve large-scale problems of our proposed model by directly applying or improving these tabu search-based algorithms.
4. Numerical Example
In order to compare our proposed TEN-based tour planning model TEN-TPP with the previous model typified by Zhu et al. [1], we provide a numerical example in this section. This example considers two candidate departure points P and Q, seven sightseeing places 1 to 7, three restaurants A to C, and four hotels a to d. These locations are shown in Figure 8. The initial satisfaction values, required times for sightseeing or having a lunch, and costs of seven sightseeing places and three restaurants are provided in the following Tables 1 and 2, respecttively. Similarly, the satisfaction values and costs of four hotels are also provided in Table 3.
As static conditions, we set the following several initial conditions:
- Tourists can go up, down, right, or left, and it takes 10 minutes to travel any compartment, i.e., it takes 30 minutes to travel between places 1 and 3.

Figure 8. Locations of departure points, sightseeing places, restaurants, and hotels.

Table 1. Initial satisfaction values, required times, and costs for sightseeing places.

Table 2. Initial satisfaction values, required times, and costs for restaurants.

Table 3. Satisfaction values and costs for hotels.
- To simplify, we assume it costs 100 yen to travel every compartment, i.e., it costs 300 yen to travel between places 1 and 3.
- Target values  and
and  in constraints (5) and (8) are set as
in constraints (5) and (8) are set as  and
and , respectively.
, respectively.
- Tourists must visit only one restaurant to have a lunch.
In this numerical example, we consider that a tourist decides the tour route from 9:20 to 16:00, i.e., 400-minute tour. This numerical example is not large-scale problem, and hence, we solve the following all problems and obtain each optimal tour route using enumeration and optimization solver. In these static conditions, we solve the previous tour planning problem not including timedependent parameters, and obtain the optimal tour route as Table 4.
From previous models, we decide visiting sightseeing places, first departure places, and accommodations, but do not directly obtain the time scheduling of the optimal tour route shown in Table 4. Therefore, we separately calculate the arrival and departure times after obtaining the optimal tour route, and obtain Figure 9. In the figure, the upper time at each place represents the arrival time, and the lower time represents the departure time.
The total satisfaction value of this tour route is 101, and the total cost is 14,900. Then, this tour route can go to almost sightseeing places except for place 6, and the tourist arrives at Hotel a at ten to 16:00. Therefore, this tour route is surely much satisfying and efficient under static conditions.

Table 4. Optimal tour route for the previous model not including time-dependent parameters.

Figure 9. Optimal tour route derived from the previous model.
However, in the case we consider the several timedependent conditions, we show that the tour route derived from the previous model is not optimal any more. The time-dependent conditions are provided as follows:
- With respect to place 1, the activity starts every hour on the hour, i.e., the activity starts at 11:00, 12:00, 13:00, etc. Therefore, even if tourists arrive at place 1 at 11:30, they must wait until 12:00.
- Consider the following several time zones:
1) From 9:20 to 11:00, we can use initial values for sightseeing places in Table 1, but all restaurants have not opened yet, and so satisfaction values for restaurants are zero in this time zone.
2) From 11:00 to 12:00, all restaurants open. On the other hand, roads going to right and left are jammed. Therefore, it takes 20 minutes to go to one right or left compartment. Furthermore, some sightseeing places are also crowded, and so required times are changed into the following required times of crowded cases in Table 5.
3) From 12:00 to 13:00, required times of all roads and sightseeing places return to initial required times. On the other hand, all restaurants are crowded, and so required times are changed into the following required times of crowded cases in Table 6.
4) From 13:00 to 14:00, required times of all restaurants return to initial required times. On the other hand, in a way similar to time zone 2), roads going to right and left are jammed again, and some sightseeing places are also crowded. These required times of crowded cases are the same as Table 5.
5) From 14:00 to 16:00, required times of all roads and sightseeing places return to initial values. With respect to restaurants A and B, the lunchtime is over, and so these restaurants are temporarily closed. Therefore, satisfaction values for restaurants A and B are 0 in this time zone.
Under these time-dependent conditions, if the tourist straightforwardly follows the tour route derived from the previous model shown in Figure 9, the following result is occurred.
Figure 10 shows that it takes 40 minutes to go from

Table 5. Required times in initial and crowded cases for some sightseeing places.

Table 6. Required times in initial and crowded cases for restaurants.
places X to 2 due to time zone 2) from 11:00 to 12:00. Furthermore, they also mean that the tourist cannot have lunch since she or he arrives at Restaurant B at 14:50, but the restaurant has already closed. Therefore, in the case that the tourist starts from P, the optimal tour route must be drastically modified as shown in Figure 11.
The total satisfaction value of this tour route decreases from 101 to 86 compared with static model Figure 9, and the total number of visiting sightseeing places also decreases from six to four.
On the other hand, in the case that the tourist deals with our proposed model TEN-TPP constructing the TEN according to the above-mentioned time-dependent conditions, the optimal tour route is obtained as the following Figure 12.
Figure 12 shows that our proposed model constructs the efficient tour route to go favorable sightseeing places, successfully avoiding crowded time zone of roads, sightseeing places and restaurant, and arriving at place 1 on time for the activity of place 1. Furthermore, comparing with the tour route in Figure 9 derived from the previous model, the total satisfaction value of our proposed model is 96 more than the previous model, and the total number of visiting sightseeing places also increases from four to five. The main differences between our proposed model and previous models are not only to consider the timedependent parameters in one network but also to select both accommodation and departure place from some candidates. With respect to the tour route shown in Figure 12, visiting sightseeing places, restaurant, and hotel is almost the same as the tour route shown in Figure 9 except for place 7, which is the lowest satisfaction value of all sightseeing places. Furthermore, the tourist also can follow the same tour route shown in Figure 12 in the case of static conditions not considering time-dependent conditions. Therefore, by selecting the departure place, our proposed model will advance the tour route as satis-

Figure 11. Optimal tour route under time-dependent condition in the case the tourist starts from P.

Figure 12. Optimal tour route derived from our proposed model under time-dependent conditions.
fying and efficient as the optimal tour route in static conditions.
5. Conclusions
In this paper, we have proposed a new personal tour planning model with time-dependent satisfaction values and traveling times. In order to represent these time-dependent parameters in the one network model and to extend the static network structure, we have introduced the Time-Expanded Network, and formulated the TEN-based mathematical programming problem. By solving our proposed model, the tourist obtains both the optimal tour route with appropriate departure place, accommodation, and the time schedule. Furthermore, by assuming the initially fixed departure place and accommodation, the proposed model has been equivalently transformed into the similar problem to previous tour planning models. Therefore, our proposed model includes previous useful tour planning models, and it is more standard model for the tour planning problem. Numerical example section also has shown that our proposed model advanced the tour route as satisfying and efficient as the optimal tour route derived from the previous tour planning problem in static conditions.
In provided numerical examples, we have mentioned that we solved our proposed model under the provided numerical examples using enumeration and optimization solver, because the examples are not so large-scale. However, with respect to the proposed models as well as general models, the problem is strongly NP-hard (Fischetti et al. [31]) due to an integer linear programming problem, and hence, it is computationally difficult to solve largescale tour planning problems using these approaches. Most recently, several algorithms have been developed to tackle the previous models, ranging from exact approaches over heuristics to meta-heuristics introduced at the end of Section 3, but it is not sufficient to develop efficient solution algorithms for the tour planning problem. Therefore, we are now studying the development of efficient heuristic solution algorithms based on soft computing approaches. Furthermore, in order to solve large-scale practical problems, we need to consider how such big data is collected, and how parameter values such as timedependent satisfaction values is more precisely set. Now, we will construct an efficient and high-precision system to overcome these drawbacks, and will apply our system to not only these practical problems for sightseeing but also the other practical network optimization problems.
REFERENCES
- C. Zhu, J. Q. Hu, F. Wang, Y. Xu and R. Cao, “On the Tour Planning Problem,” Annals of Operations Research, Vol. 192, No. 1, 2012, pp. 67-86. doi:10.1007/s10479-010-0763-5
- R. A. Abbaspour and F. Samadzadegan, “Time-Dependent Personal Tour Planning and Scheduling in Metropolises,” Expert Systems with Applications, Vol. 38, No. 10, 2011, pp. 12439-12452. doi:10.1016/j.eswa.2011.04.025
- W. Souffriau, P. Vansteenwegen, J. Vertommen, G. V. Berghe and D. V. Oudheusden, “A Personalized Tourist Trip Design Algorithm for Mobile Tourist Guides,” Applied Artificial Intelligence, Vol. 22, No. 10, 2008, pp. 964-985. doi:10.1080/08839510802379626
- K. G. Zografos and K. N. Androutsopoulos, “Algorithms for Itinerary Planning in Multimodal Transportation Networks,” IEEE Transactions on Intelligent Transportation System, Vol. 9, No. 1, 2008, pp. 175-184. doi:10.1109/TITS.2008.915650
- W. Bohte and K. Maat, “Deriving and Validating Trip Purposes and Travel Modes for Multi-Day GPS-Based Travel Surveys: A Large-Scale Application in the Netherlands,” Transportation Research Part C: Emerging Technologies, Vol. 17, No. 3, 2009, pp. 285-297. doi:10.1016/j.trc.2008.11.004
- D. Ettema, T. Garling, L. E. Olsson and M. Friman, “Outof-Home Activities, Daily Travel and Subjective WellBeing,” Transportation Research Part A: Policy and Practice, Vol. 44, No. 9, 2010, pp. 723-732. doi:10.1016/j.tra.2010.07.005
- T. Y. Hu, C. C. Tong, T. Y. Liao and W. M. Ho, “Simulation-Assignment-Based Travel Time Prediction Model for Traffic Corridors,” IEEE Transactions on Intelligent Transportation Systems, Vol. 13, No. 3, 2012, pp. 1277- 1286. doi:10.1109/TITS.2012.2190061
- A. Khosravi, E. Mazloumi, S. Nahavandi, D. Creighton and J. W. C. Van Lint, “Prediction Intervals to Account for Uncertainties in Travel Time Prediction,” IEEE Transactions on Intelligent Transportation Systems, Vol. 12, No. 2, 2011, pp. 537-547. doi:10.1109/TITS.2011.2106209
- X. Cai, D. Sha and C. K. Wong, “Time-Varying Universal Maximum Flow Problems,” Mathematical and Computer Modelling, Vol. 33, No. 4-5, 2001, pp. 407-430. doi:10.1016/S0895-7177(00)00252-1
- M. Florian, G. Bushell, J. Ferland, G. Guerin and L. Nastansky, “Engine Scheduling Problem in a Railway Network,” Canadian Journal of Operational Research and Information Processing, Vol. 14, No. 2, 1976, pp. 121- 138.
- D. J. Zawack and L. T. Gerald, “Dynamic Space-Time Network Flow Model for City Traffic Congestion,” Transportation Science, Vol. 21, No. 3, 1987, pp. 153-162. doi:10.1287/trsc.21.3.153
- F. G. Engineer, G. L. Nemhauser and M. W. P. Savelsgergh, “Dynamic Programming-Based Column Generation on Time-Expanded Network: Application to the Diala-Flight Problem,” INFORMS Journal on Computing, Vol. 23, No. 1, 2011, pp. 105-119. doi:10.1287/ijoc.1100.0384
- Y. Guo, T. Mellouli, L. Suhl and M. P. Thiel, “A Partially Integrated Airline Crew Scheduling Approach with TimeDependent Crew Capacities and Multiple Home Bases,” European Journal of Operational Research, Vol. 171, No. 3, 2006, pp. 1169-1181. doi:10.1016/j.ejor.2005.01.024
- C. Hane, C. Barnhart, E. L. Johnson, R. E. Marsten, G. L. Nemhauser and G. Sigismondi, “The Fleet Assignment Problem: Solving a Large Integer Program,” Mathematical Programming, Vol. 70, No. 2, 1995, pp. 211-232. doi:10.1007/BF01585938
- N. Kliewer, T. Mellouli and L. Suhl, “A Time-Space Network Based Exact Optimization Model for Multi-Depot Bus Scheduling,” European Journal of Operational Research, Vol. 175, No. 3, 2006, pp. 1616-1627. doi:10.1016/j.ejor.2005.02.030
- N. Shah, S. Kumar, F. Bastani and I. L. Yen, “Optimization Models for Assessing the Peak Capacity Utilization of Intelligent Transportation Systems,” European Journal of Operational Research, Vol. 216, No. 1, 2012, pp. 239- 251. doi:10.1016/j.ejor.2011.07.032
- S. Yan and C. Y. Chen, “An Optimization Model and a Solution Algorithm for the Many-to-Many Car Pooling Problem,” Annals of Operations Research, Vol. 191, No. 1, 2011, pp. 37-71. doi:10.1007/s10479-011-0948-6
- J. C. Chu, S. Yan and K. L. Chen, “Optimization of Earth Recycling and Dump Truck Dispatching,” Computers & Industrial Engineering, Vol. 62, No. 1, 2012, pp. 108-118. doi:10.1016/j.cie.2011.08.022
- J. J. Jarvis and H. D. Ratliff, “Some Equivalent Objectives for Dynamic Network Flow Problems,” Management Science, Vol. 28, No. 1, 1982, pp. 106-109. doi:10.1287/mnsc.28.1.106
- M. R. Silver and O. L. de Weck, “Time-Expanded Decision Networks: A Framework for Designing Evolvable Complex Systems,” Systems Engineering, Vol. 10, No. 2, 2007, pp. 167-186. doi:10.1002/sys.20069
- M. Fischetti, J. S. Gonzalez and P. Toth, “Solving the Orienteering Problem through Branch-and-Cut,” INFORMS Journal on Computing, Vol. 10, No. 2, 1998, pp. 133-148. doi:10.1287/ijoc.10.2.133
- I. M. Chao, B. L. Golden and E. A. Wasil, “A Fast and Effective Heuristic for the Orienteering Problem,” European Journal of Operational Research, Vol. 88, No. 3, 1996, pp. 475-489. doi:10.1016/0377-2217(95)00035-6
- J. L. Kennington and C. D. Nicholson, “The Uncapacitated Time-Space Fixed-Charge Network Flow Problem; an Empirical Investigation of Procedures for Arc Capacity Assignment,” INFORMS Journal of Computing, Vol. 22, No. 2, 2009, pp. 326-337. doi:10.1287/ijoc.1090.0354
- Q. Wang, X. Sun, B. L. Golden and J. Jia, “Using Artificial Neural Networks to Solve the Orienteering Problem,” Annals of Operations Research, Vol. 61, No. 1, 1995, pp. 111-120. doi:10.1007/BF02098284
- M. Gendreau, G. Laporte and F. Semet, “A Tabu Search Heuristic for the Undirected Selective Traveling Salesman Problem,” European Journal of Operational Research, Vol. 106, No. 2-3, 1998, pp. 539-545. doi:10.1016/S0377-2217(97)00289-0
- H. Tang and E. Miller-Hooks, “A Tabu Search Heuristic for the Team Orienteering Problem,” Computers & Operations Research, Vol. 32, No. 6, 2005, pp. 1379-1407. doi:10.1016/j.cor.2003.11.008
- L. Ke, C. Archetti and Z. Feng, “Ants Can Solve the Team Orienteering Problem,” Computers & Industrial Engineering, Vol. 54, No. 3, 2008, pp. 648-665. doi:10.1016/j.cie.2007.10.001
- P. Fattahi, M. S. Manesh and A. Roshani, “A New Solution Seed for Job Shop Scheduling Problem,” Applied Mechanics and Materials, Vol. 110-116, 2012, pp. 3899- 3905.
- M. Seker and N. Noyan, “Stochastic Optimization Models for the Airport Gate Assignment problem,” Transportation Research Part E: Logistics and Transportation Review, Vol. 48, No. 2, 2012, pp. 438-459. doi:10.1016/j.tre.2011.10.008
- J. Elias, F. Martignon and G. Carello, “Very Large-Scale Neighborhood Search Algorithm for the Design of Service Overlay Networks,” Telecommunication Systems, Vol. 49, No. 4, 2012, pp. 391-408. doi:10.1007/s11235-010-9381-4
- M. Fischetti, J. J. Salazar-González and P. Toth, “The Generalized Traveling Salesman and Orienteering Problems,” In: G. Gutin and A. P. Punnen, Eds., The Traveling Salesman Problem and Its Variations, Kluwer Academic Publisher, Dordrecht, 2002, pp. 609-662.




