Journal of Biosciences and Medicines
Vol.03 No.09(2015), Article ID:59660,7 pages
10.4236/jbm.2015.39003
A Preliminary Study on Spatial Spread Risk of Epidemics by Analyzing the Urban Subway Mobility Data
Bu Zhao1, Shunjiang Ni1,2*, Nuo Yong1,2, Xun Ma1,2, Shifei Shen1,2, Xuewei Ji3
1Department of Engineering Physics, Tsinghua University, Beijing, China
2Institute of Public Safety Research, Tsinghua University, Beijing, China
3Beijing Academy of Safety Science and Technology, Beijing, China
Email: *sjni@tsinghua.edu.cn


Received 21 July 2015; accepted 10 September 2015; published 17 September 2015

ABSTRACT
The prevention and treatment of epidemic is always an urgent problem faced by the human being. Due to the special space structure, huge passenger flow and great people mobility, the subway lines have become the areas with high epidemic transmission risks. However, there is no recent study related to epidemic transmission in the subway network on urban-scale. In this article, from the perspective of big data, we study the transmission risk of epidemic in Beijing subway network by using urban subway mobility data. By reintegrating and mining the urban subway mobility data, we preliminary assess the transmission risk in the subway lines from the passenger behaviors, station features, route features and individual case on the basis of subway network structure. This study has certain practical significance for the early stage of epidemic tracking and prevention.
Keywords:
Urban Subway, Human Mobility, Epidemic Spread, Risk Assessment

1. Introduction
In the history, epidemic has always been a serious threat to human health. The prevention and treatment of epidemic is always an urgent problem faced by the human being. As the MERS is spreading nowadays, the prevention and suppression of similar epidemic is a significant responsibility of the government and the medical department. In the view of system science, the outbreak of epidemic can be understood as a complex diffusion process in the crowd. The modeling and assessment of this process can help us to understand the mechanism of the spread of epidemic and provide corresponding basis of epidemic analysis, simulation and interference [1].
The traditional epidemic assessment and prediction method is based on the differential equation. And the most mature and commonly used model is the SIR, SIRS and SIS. In recent years, the researches on the spread of epidemic are being deepened and refined [2]-[11]. In the model, there is a transition from the single Chamber model to the complex network model with the addition of relationship network, which leads to a greatly improvement on the reliability and rationality of the results. On the other hand, due to the comprehensive improvement of traffic network, the popularization of transportation (aviation transportation, railway transportation, road transportation, etc.) makes the contact between people become easier and more complex. As a result, the transmission of epidemic in transportation network is gradually concerned by researchers [12].
However, the researches of transportation network are basically aviation network based on modeling method. And the object is always focused on national and global scale. There is no recent study related to the epidemic transmission in the subway network on urban-scale. Therefore, it is meaningful and valuable to reconstruct the subway flow information and build risk assessment of different routes and stations by using the idea of big data.
2. Data and Method
2.1. Data
In the process of taking a subway, passengers will use the Beijing municipal administration & communication card or a one-way subway ticket. So the card machine in the station can record a large number of card information every day. In this article, we use the data from the official card system. The data we used contains 1 day smart card data, namely one day in February, 2014. The number of the original data records is 3,249,333. In order to facilitate the subsequent research, we need to eliminate the ineffective information from the original data and save into our own format. The number of the final data is 1,630,213 and the content is showed in Table 1.
2.2. Method
In order to carry out a risk assessment of the spread of epidemic from both macroscopic and microcosmic, it is necessary to make full use of the existing data resources. This study uses the C++ programming to mine and count the general passenger flow information and the corresponding hidden information.
3. Results
3.1. Passenger Behavior
The stops number and cost time of the passengers are satisfied with the normal distribution, as shown in Figure 1, the probability density function expression of the distribution is
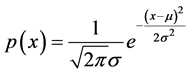 . (1)
. (1)
In the stops number distribution, 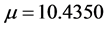 ,
,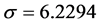 . And in the cost time distribution,
. And in the cost time distribution, 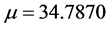 ,
,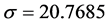 . We can find that most passengers prefer to choose the journey of medium length (10 stops or 30 minutes), 90% of the passengers’ stops number is less than 20 and cost time is less than 60 minutes. Most of the passengers (86%) only take subway once in a day. Besides of it, there are still a small part of the passengers (13%) will take the subway twice in a day and most of them (69%) choose the round-trip travel. Three and more only account for 1% and can be neglected.
. We can find that most passengers prefer to choose the journey of medium length (10 stops or 30 minutes), 90% of the passengers’ stops number is less than 20 and cost time is less than 60 minutes. Most of the passengers (86%) only take subway once in a day. Besides of it, there are still a small part of the passengers (13%) will take the subway twice in a day and most of them (69%) choose the round-trip travel. Three and more only account for 1% and can be neglected.
The results show that most of the passengers choose short or medium distance journeys and most of them only
Table 1. The final single data record format.
take subway once in a day. Therefore, there is a huge number of people exchange in the subway lines every day. If there is an infectious case, a cross-spread situation may emerge easily in this region.
For the number of arrival passengers that exit the station, the distribution is shown in Figure 2, where each station number represents a site in the abscissa. The results showed that a total of 10 stations’ number is more than 20,000, 37 stations’ number is more than 10,000 but less than 20,000, 88 stations’ number is more than 5000 but less than 10,000, 100 stations’ number is less than 5000. The total number of the stations with the passengers’ number of more than 10,000 is close to the half of all. This shows that the stations where the passengers choose to get off are relatively concentrated. After analyzing the location of these stations, we can find these stations are located in the area with the train stations, transportation hubs, commercial centers, medical institutions, places of interest and residential areas.
For the total passengers’ flow that passing through the station (containing the parts of passengers passing by, getting in and getting off the station), the distribution is also shown in Figure 2. The results showed that a total of 22 stations’ flow number is more than 200,000, 52 stations’ flow number is more than 100,000 but less than 200,000, 61 stations’ flow number is more than 50,000 but less than 100,000, 100 stations’ flow number is less than 50,000. The stations with large passengers’ flow relatively concentrate in the region of middle. After analyzing, there are 74 stations with the flow number of more than 100,000. If we select the highest 10 sets of data, it can be found that these stations are all large transfer stations with a daily flow of more than 250,000, which perfectly matching our knowledge.
Figure 1. The distribution of the cost time and stops number of the passengers.
Figure 2. The passenger number of the arrival & exit and total passenger flow.
In the following analysis, we believe that on average, the greater the passenger flow of the site, the greater the risk of transmission of infectious diseases for the site area.
3.2. Station Risk Assessment
For the passenger source for a certain destination station (take the Beijing Railway Station as example), the distribution is shown in Figure 3. The results show that only 6 stations have over 1000 passengers whose destination is the Beijing railway station, 21 stations’ number is more than 500 but less than 1000, 208 stations’ number is less than 500 people. Therefore, the passenger source is relative concentrated for most of passengers are from 27 stations. After analyzing the location of these stations, we can find these stations are all in the area with many communities, such as TIANTONGYUAN, HUILONGGUAN, PINGUOYUAN, etc. It can be understood as the passengers go to the Beijing Railway Station from their residence.
For the passengers from the same station, the distribution of destination stations is shown in Figure 4, which is relatively dispersed. The study shows that only 1 station’s passenger number is more than 1000, 6 stations’ number is more than 500 but less than 1000, 228 stations’ number is less than 500 people. Therefore, there are only 7 stations with relative many passengers and these stations are also in the area with train stations, transportation hubs, commercial centers, medical institutions, places of interest and residential areas.
3.3. Route Risk Assessment
Due to the existence of different route choices, different passengers may choose different ways to reach the same destination. The article shows that the passenger flow varies greatly between the different routes of two stations. In general, we can divide the route features into two categories. One is the stations with a clear shortest route and the other is the stations with competitive route. There are significant differences in the statistical results of these two lines, which is shown in Figure 5.
For the first route feature, the article takes the HAIDIANHUANGZHUANG to WUDAOKOU as an example. The red, grey and yellow lines represent the shortest, second and third shortest route. The results show that basically all the passengers (95.6%) choose one route (the shortest route), which matching our common sense.
Figure 3. The hot spot diagram of the passenger source.
Figure 4. The hot spot diagram of the passenger whereabouts.
For the second route feature, the article takes the CAISHIKOU to CHAOYANGMEN as an example. The red, grey and yellow lines represent the shortest, second and third shortest route. Unlike the previous one-sided distribution, the results show that there is no marked difference between the passenger numbers of the three routes. These results are reasonable because of the similar length of the three routes.
Therefore, when it is unable to determine the actual passenger choice of routes, due to the different proportion of passenger choices, the route with a high choice proportion earn a high level of transmission risk. They belong to the area with high epidemic transmission risk.
3.4. Individual Case Tracking
According to the route matching principle, by comparing the potential routes and the cost time, we can get one certain infectious individual’s actual choice of the route and the new contact individuals in each station, which is showed below: Beijing South Railway Station (218)- >TAORANTING (61)- >CAISHIKOU (20)- >XUANWU- MEN (69)- >HEPINGMEN (23)- >QIANMEN (51)- >CHONGWENMEN (92)- >CIQIKOU (46), where figures in brackets represent the number of potential contact individuals with the tracking case.
The total number of the people who have a potential contact with the tracking infectious case is 580. By this method, we can obtain the urban subway mobility data information of the contact individuals, which can help us to determine suspected close contact persons. It is quite significant for us to take corresponding measures. Part of the contact individuals’ card information is showed in Table 2.
4. Conclusion
In this study, using the big data sight, we make a preliminary research and analysis on the epidemic transmission risk of Beijing subway line through the perspective of passenger behavior, station, route, and the individual case. The article summaries the passengers’ traveling behavior and reflects its rules; We also analyze the stations’ source and whereabouts features by counting the urban subway mobility data and finally finish the macroscopic station epidemic transmission risk assessment; Subsequently, by using the travel route algorithm and the route matching principle, we obtain the passenger’s actual travel route and the macroscopic epidemic transmission
Figure 5. The distribution of the route passengers
Table 2. Part of the contact individuals’ card information.
risk assessment of different routes; Finally, we track a hypothetical case and get its influence range, through which we fulfill a microcosmic risk assessment. In this article, we have carried on a preliminary exploration of the above questions and obtained some valuable conclusions. The future work can be deepened and refined through this method.
Acknowledgements
This study was funded by the National Natural Science Foundation of China (No. 71203118) and the Research on the development strategy of national public safety science and technology (No. 2014-ZD-02).
Cite this paper
Bu Zhao,Shunjiang Ni,Nuo Yong,Xun Ma,Shifei Shen,Xuewei Ji, (2015) A Preliminary Study on Spatial Spread Risk of Epidemics by Analyzing the Urban Subway Mobility Data. Journal of Biosciences and Medicines,03,15-21. doi: 10.4236/jbm.2015.39003
References
- 1. Grassly, N.C. and Fraser, C. (2008) Mathematical Models of Infectious Disease Transmission. Nature Reviews Microbiology, 6, 477-487. http://dx.doi.org/10.1038/nrmicro1845
- 2. Anderson, R.M. and Roy, R.M. (1991) Infectious Diseases of Humans. Oxford University Press, Oxford.
- 3. Watts, D.J. and Strogatz, S.H. (1998) Collective Dynamics of “Small-World” Networks. Nature, 393, 440-442. http://dx.doi.org/10.1038/30918
- 4. Moore, C. and Newman, M.E.J. (2000) Epidemics and Percolation in Small-World Networks. Physical Review E, 61, 5678-5682. http://dx.doi.org/10.1103/PhysRevE.61.5678
- 5. Kleczkowski, A. and Grenfel, B.T. (1999) Mean-Field-Type Equations for Spread of Epidemics: The “Small World” Model. Physica A, 274, 355-360. http://dx.doi.org/10.1016/S0378-4371(99)00393-3
- 6. Pastor-Satorras, R. and Vespignani, A. (2001) Epidemic Spreading in Scale-free Networks. Physical Review Letters, 86, 3200-3203. http://dx.doi.org/10.1103/PhysRevLett.86.3200
- 7. Pastor-Satorras, R. and Vespignani, A. (2001) Epidemic Dynamics and Endemic States in Complex Networks. Physical Review E, 63, 1-9. http://dx.doi.org/10.1103/physreve.63.066117
- 8. Xia, C.Y., Liu, Z.X., Chen, Z.Q. and Yuan, Z.Z. (2009) Spreading Behavior of SIS Model with Non-Uniform Transmission on Scale-Free Networks. The Journal of China Universities of Posts and Telecommunications, 16, 27-31. http://dx.doi.org/10.1016/S1005-8885(08)60173-9
- 9. Newman, M.E.J. (2002) The Spread of Epidemic Disease on Networks. Physical Review E, 66, 1-12. http://dx.doi.org/10.1103/physreve.66.016128
- 10. Abramson, G. and Kuperman, M. (2001) Small World Effect in an Epidemiological Model. Physical Review Letters, 86, 1-4.
- 11. Moreno, Y., Gomez, J.B. and Pacheco, A.F. (2003) Epidemic Incidence in Correlated Complex Networks. Physical Review E, 68, 1-4. http://dx.doi.org/10.1103/physreve.68.035103
- 12. Grais, R.F., Ellis, J.H. and Glass, G.E. (2003) Assessing the Impact of Airline Travel on the Geographic Spread of Pandemic. European Journal of Epidemiology, 18, 1065-1072.
NOTES

*Corresponding author.







