Energy and Power Engineering, 2009, 54-64
doi:10.4236/epe.2009.11009 Published Online August 2009 (http://www.scirp.org/journal/epe)
Optimal Scheduling Strategy for Energy Consumption
Minimization of Hydro-Thermal Power Systems
Jiekang WU
School of Electrical Engineering, Guangxi University, Nanning, China
Abstract: A comparison analysis based method for computing the water consumption volume needed for
electric energy production of optimal scheduling in hydro-thermal power systems is presented in this paper.
The electric energy produced by hydroelectric plants and coal-fired plants is divided into 4 components: po-
tential energy, kinetic energy, water-deep pressure energy and reservoir energy. A new and important concept,
reservoir energy, is proposed, based on which is divided into a number of water bodies, for example 3 water
bodies, and a reservoir is analyzed in a new way. This paper presents an optimal scheduling solution of elec-
tric energy production of hydro-thermal power systems based on multi-factors analytic method, in which
some important factors, such as load demand, reservoir in-flow, water consumption volume increment rate of
hydroelectric plants or converted from coal-fired plants, and so on are given to model the objective function
and the constraints. A study example with three simulation cases is carried out to illustrate flexibility, adapta-
bility, applicability of the proposed method.
Keywords: hydro-thermal power systems, optimal electric energy production, water consumption volume
1 Introduction
Water is one of the important renewable energy sources
and coal is a non-renewable energy source. For optimal
scheduling of hydro-thermal power systems, it is the first
thing that water must have much more priority to be used
for electric energy production than coal so as to supply
the demand load. It is an important study task how to
minimize the sum of water consumption volume of the
hydroelectric plant and water consumption volume con-
verted from the coal-consumed volume of coal-fired
plants in hydro-thermal power system dispatch.
In modeling electric energy production of hydroelec-
tric plants, some pioneer did many significant works. For
the portfolio management of a scandinavian power sup-
plier, a linear stochastic model with hydraulic power
plants under uncertain inflow and market price condi-
tions is introduced [1]. In [2], price uncertainty by sce-
narios and a model for maximizing risk-adjusted profit
within an asset-liability framework is represented. A new
multi-loop-cascaded governor, with which the perform-
ance specifications and stability margins are improved
significantly even in the presence of some uncertainties,
is proposed to use for hydro turbine control [3] and some
other stochastic programming models are proposed to
represent the energy systems [4]. However, with the
achievements in recent liberalization of the electricity
market, the discussion about improving the assumptions
and considering further aspects of actual system opera-
tions is far from ending.
Some works have done for the optimal scheduling so-
lution of hydro-thermal power systems. There are many
computational methods for the solution of some difficult
optimization problem such as dynamic programming
[5][6], network flow [7-9], standard mixed integer pro-
gramming methods [10-12], and modern heuristic algo-
rithms [13][14]. Although dynamic programming is
flexible and can handle the constraints better in a
straightforward way, the “curse of dimensionality” still
remains, and the main drawback of using dynamic pro-
gramming for a realistic systems with multiple reservoirs

J. K. WU
55
and cascaded hydro plants still exists [14]. Network flow
would be the natural way to model hydro systems. Its
main drawback, however, is its inability to deal with
discontinuous operating regions and discrete operating
states [15]. Mixed integer programming is only suitable
for small systems due to size limitations. Modern heuris-
tic algorithms do not require such conditions that the
objective function has to be differentiable and continu-
ous, so these methods are considered as effective tools
for non- linear optimization problems such as short-term
scheduling of hydro systems. Particle swarm optimiza-
tion (PSO) is one of the modern heuristic algorithms.
PSO has attracted great attention due to its features of
easy implementation, robustness to control parameters
and computation efficiency compared with other existing
heuristic algorithms, and has been successfully applied to
hydroelectric optimization scheduling problems [16-20].
Some stochastic approaches are also used for the solution
of the cascaded hydro plants problem [21-22].
This paper presents a novel analysis method for mod-
eling hydro-energy conversion and computing water con-
sumption volume of optimal electric energy production in
large-scale hydro-thermal power systems, taking some
energy components, such as potential energy, kinetic en-
ergy, water-deep pressure energy and reservoir energy
into consideration, and also taking some influence factors,
such as load demand, reservoir in-flow, water consump-
tion volume increment rate, and so on, into account.
2 Hydro-Energy Conversion
In a large-scale reservoir, if there is a hydro-mechani-
cal-electric coupling system, with a shaft leading the
reservoir water through penstock to a hydro turbine,
the potential, kinetic and water-deep energy in water
is harnessed by the HME coupling system and create
electricity from it. For each HME system, the amount
of electric energy transformed form hydro energy in
reservoir depends on the forces applied on the water
body in intake and tailrace of the pressure tunnel. In
intake of the pressure tunnel, basing on the traditional
analysis method, there is gravitational force corre-
sponding to the potential energy, kinetic force corre-
sponding to kinetic energy and pressure force corre-
sponding to water-deep pressure energy.
In this paper, besides three traditional forces there are
another three reservoir forces applied to the water body
in intake if a reservoir is divided into three water bodies
when modeling the hydroelectric energy of large-scale
reservoir. These three reservoir forces applies to the wa-
ter bode in intake of a pressure tunnel and do work in
respective part, which is called ‘reservoir energy’ in this
paper, as shown in Figure 1.
),( txH j
ij,

ijO
H,,
xdij A,
ijI
H,,
ij,

x
y
js
X,
jm
X,
je
X,
jm
H,WB1WB2
WB3
Figure 1. Divided water bodies of a large-scale reservoir

J. K. WU
56
Because of difference in kinetic energy, potential en-
ergy, energy converted from water-deep pressure energy,
the energy converted from self-weight, reservoir energy,
there is a part of energy transformed into electric energy.
For a unit in plant , the electric energy converted
by a HME system in unit time(for example one second)
may be expressed in a form of kilo-watt may be formu-
lated in MWs:
ij
654321,,,, ),( ffffffQHE ijGjijH

 (1)
where
ijGijOijIj QpHtxHf ,,,,,,1 ]))),([(81.9 (2)
ijGijOijI Qvv
g
f,,
2
,,
2
,,2 ][
2
1
*81.9  (3)
ijGijOijI QtHHf ,,,,,,3 )]([81.9 (4)



]),([
]),([81.9
,,
,,,
4
ijIjj
ijIjjjs
HtxHY
HtxHYX
f
ijGijsjsijIjs Q,,,,
2
,,,, cos)cos(sin 

(5)



]),([2
)),(2)((81.9
,,
,,,,,
5
ijIjj
ijIjmjjsjmj
HtxHY
HHtxHXXY
f
ijGijmjmijIjmQ,,,,
2
,,,, cos)cos(sin 

(6)



]),([3
)),()((81.9
,,
,,,
6
ijIjj
jmjjmjej
HtxHY
HtxHXXY
f
ijGijejeijIjeQ,,,,
2
,,,, cos)cos(sin 
 (7)
where is energy converted from water-deep pressure
energy, is energy converted from kinetic energy,
is energy converted from potential energy, -
is energy converted from reservoir energy. is gen-
eration flow of generator in plant ,
1
f
f2
3
f4 f
i
6
f
jG
Q,,
ij,
i j

is the
angle of the pressure tunnel for each generating unit,
is water-storage level elevation in reservoir
at time
)t,(xH jj
t
, is a position elevation of the intake of
the pressure tunnel relative to sea level,
ijI
H,,
js,

,jm,

and
je,

is angle between
x
direction and the line passing
through the gravity center of water body WB1, WB2,
WB3 and axial origin respectively, and is
diameter and sectional area of the pressure tunnel in the
intake respectively, denotes plant index, ,
and is starting point of water body WB1, WB2
and WB3 in
ij
D,ij A,
m
X,
jjs
X,j
je
X,
x
direction, is width of the dam,
j
Y
i,js,

, ij,m,

and ije ,,

is angle of the water body WB1,
WB2 and WB3 between the center line of
x
direction
and the pressure tunnel of unit in reservoir re-
spectively, is maximal utilization hours for the
rated capacity of hydroelectric generating unit i in hy-
droelectric plant j, N year number of a schedul-
ing period.
ij
ij,max,
T
jR,i
H
P,
s
The electric power of a generator is formu-
lated:
i,j
T
E
Pij,,H
ijH ,, (8)
where
T
is scheduling period of the hydroelectric
plants.
For a unit time( one second), .
i,
Q
jH
E, 
f6]
ijH ,,
f
P
f4
3 Energy Consumption of Electric Power
Production
3.1 Water Consumption Volume Increment Rate
For a hydropower-driven generator, the variation of elec-
tric energy is obtained by differentiating Equation (1)
with respect to :
ij,
f2
G,
Q
f1ijG ,,ijH E,, f3 5 [










ijH
W
T
f6 
])
i
f5
,O
p
f4
)
,ij 
ff 2
(x
f
81.
,,
3
I
H
1
[(

),t

j
H

9
1
f
(23)
where
,,j



(24)
]
,,ij
)]t
[i
,ij
2
1
*g
,
HI
81.
[81
9
2
f
.9
3
f
2
O
2
,, jI
v
H
v
,, ijO
(25)
( (26)

J. K. WU
57



 ]),([
]),([81.9
,,
,,,
4
ijIjj
ijIjjjs
HtxHY
HtxHYX
f
ijsjsijIjs ,,
2
,,,, cos)cos(sin
  (27)



 ]),([2
)),(2)((81.9
,,
,,,,,
5
ijIjj
ijIjmjjsjmj
HtxHY
HHtxHXXY
f
ijmjmijIjm ,,
2
,,,, cos)cos(sin
  (28)



 ]),([3
)),()((81.9
,,
,,,
6
ijIjj
jmjjmjej
HtxHY
HtxHXXY
f
ijejeijIje ,,
2
,,,, cos)cos(sin
  (29)
Water consumption volume increment rate is defined
to be a ratio of the variation of the water consumption
volume and the variation of electric power output of a
hydropower-driven generator:
654321,,
,,
,, ffffff
T
E
W
ijH
ijH
ijH 





ijG
ijG
Qffffff
QT
,,654321
,,
)( 


ijH
ijG
E
QT
,,
,,


 (30)
3.2 Coal Consumption Volume Increment Rate
For a thermal power-driven generator, the coal consump-
tion volume is formulated as a quadratic function of
electric power, as shown in the following form:
lkTlkTlkTlkTlkTlkT cEbEaF ,,,,,,
2
,,,,,,  (31)
where and is respectively coal consump-
tion volume and electric power of a thermal
power-driven generator; ,, is respec-
tively coefficient of coal consumption volume of a ther-
mal power-driven generator.
lkT
F,, lkT E,,
lkT
a,, lkT b,, lkT c,,
The variation of coal consumption volume is obtained
by differentiating Equation (25) with respect to:
ijT
E,,
lkTlkTlkTlkTlkT EbEaF ,,,,,,,,,, )2( 

 (32)
Coal consumption volume increment rate is defined to
be a ratio of the variation of the coal consumption vol-
ume and the variation of electric power output of a ther-
mal power-driven generator:
lkTlkTlkT
lkT
lkT
lkT bEa
E
F
,,,,,,
,,
,,
,, 2


  (33)
4 Optimal Scheduling Models for Hydro-
Thermal Systems
Water is one of renewable energy, which is an energy
source that can be replenished in a short period of time,
and is mainly used for electric energy production. Coal is
non-renewable energy, which is an energy source that
may be used up and cannot be recreated in a short period
of time. In order to make as possible as best use of re-
newable resource, water must be placed on more prior
consideration for electric energy production than coal.
For this purpose, the objective of scheduling optimiza-
tion of hydro-thermal power systems must minimize the
water consumption volume consumed in electric energy
production, including the water consumption volume
consumed in hydro-electric plants and the water con-
sumption volume exchanged from coal consumption
volume consumed in coal-fired electric plants:
][min
11
,,,,
111
,,  
TTG
HHG N
k
N
l
lkTlkT
T
t
N
j
N
i
ijH FW
 (34)
where and is respectively number of hy-
droelectric plants and hydro-driven generators in plant
, and is respectively number of coal-fired
electric plants and coal-fired generators,
H
N
T
HG
N
TG
jN N
lkT ,,

is a co-
efficient exchanging coal consumption volume con-
sumed in coal-fired electric plants into water consump-
tion volume, and it is formulated:
lkTlkT
advH
lkT EF ,,,,
,
,, 



(35)
where advH,

is average water consumption volume
increment rate of all hydro-driven generators:

J. K. WU
58
HGH
N
j
N
i
ijH
advH NN
HHG


11
,,
,

 (36)
The constraint conditions include:
1) Equality constraint for electric power of hy-
dro-thermal power systems: at any time
t
, the sum of
the electric power produced by hydro-driven generators
and coal-fired generators must be hold to be equal to
load-demanded power:
0)()()(
11
,,
11
,,   
tPtPtP L
N
k
N
l
lkT
N
j
N
i
ijH
TTG HHG
(37)
where is load-demanded power at any time )(tPL
t
.
2) Equality constraint for electric energy of hy-
dro-thermal power systems: in the scheduling period
T
,
the sum of the electric energy produced by hydro-driven
generators and coal-fired generators must be hold to be
equal to load-demanded energy:
0)()()(
11
,,
11
,,  
TETETE L
N
k
N
l
lkT
N
j
N
i
ijH
TTG HHG
(38)
where is load-demanded energy in the schedul-
ing period
)(TE L
T
.
3) Inequality constraint for active and reactive power
of hydro-driven generators:
ijH
ijH ijH PPP ,, ,, ,,  (39)
ijH ijH
ijH QQQ ,,
,,
,,  (40)
where ijH P,, ,ijH
Q,, and ijH P,, , ijH Q,, is respec-
tively the lower and upper limited value of active and
reactive power of hydro-driven generator in plant . ij
5) Inequality constraint for active and reactive power
of coal-fired generators:
lkT
lkT lkT PPP ,, ,, ,,  (41)
lkT
lkT
lkT QQQ,,
,,
,,  (42)
is respec-
e low and imitealue otively therupper ld vf active and
where lkT P,,,lkT Q,,
reactive power of coal-fired generator l in plant k.
6) Inequality constraint for generation flow:
ijG
ijG
ijG QQQ ,,
,,
,,  (43)
where and ijG
Q,,
ijG
Q,, is respectively
imited value of ge
r in
where and is maximal limit and minimal
ption vol-
um
(45)
where and is maximal limit and minimal
the lower and
upper lneration flow of hydro-driven
generato plant
7) Inequality constraint for coal consumption volume:
ij.
kup
l
lkTkdown FFF ,
1
,,,  

NTG
(44)
kup
F,kdown F,
mptionlimit of coal consu volume of coal-fired electric
plant k in the scheduling period T.
8) Inequality constraint for water consum
e:
jup
N
i
ijHjdown WWW
HG
,
1
,,,  

jup
W,
f wat
j in th
jdown
W,
sumpti
duling
limit oer conon volume of hydro-electric
plant e scheperiod
T
.
9) Inequality constraint for wateronsumption volume c
an
(46)
where
d coal consumption volume: for a whole, the coal con-
sumption volume exchanged using water consumption
volume of all hydro-driven generators is required to be
greater than that consumed by all coal-fired generators:
TNN
TNNTTG
HHG 

t kl
lkT
t j i
ijHijC FW
111
,,
111
,,,,

ijC,,

is a coefficient exchanging water con-
n volsumptioume consumed in hydro-electric plants into
coal consumption volume, and it is formulated:
ijHijH
advT
ijC EW ,,,,
,
,, 


 (47)
where advT ,

is average coal consumption volume
rate oincrementf all coal-fired generators:
and lkT P,, , lkT Q,,

J. K. WU
59
TGT
NN
lkT
TTG
 ,,

k l
advT NN

11
,

(48)
At the same time, the water consumption volume ex-
ch
(49)
10) Equality constraint related to saved-water level:
du
(50)
where , and is a re-
aved-wr levelt time
anged from coal consumption volume of all coal-fired
generators is required to be smaller than that consumed
by all hydro-driven generators:
TTNN
HHG 

t
N
k
N
l
lkTlkW
tji
ijH
TTG
FW
111
,,,,
111
,,

ring high-water period, normal-water period, low wa-
ter period, and flood period, saved-water level is re-
quired to be retained at a fixed value:
fo
H







FPfor
NPfor
HPfor
LPr
)(
,
,
,
,
jFP
jNP
jHP
jLP
j
H
H
H
tH
jLP
H,jHP H,,jNP H,jFP H,
quired sate a
t
in ir j for reservo
tion of saved-water
le
high-water period, normal-water period, low water pe-
riod, and flood period respectively.
11) Equality constraint for varia
vel: in the scheduling period
T
, the variation of
saved-water level in reservoir j is required to be equal
to zero:
0)(
11



T
t
N
j
j
H
tH (51)
12) Inequality constraint for water energy total: at time
t
, the water energy total of cascaded hydroelectric plants
required to be no smaller than a designed value:
NN
HHG
is
(52)
where is designed value of the water energy total of
d h
(53)
where and is respectively the des
nr inimal saved-water
le
A
j i
ijGjijHijjR EQHETN 

11
,,,,,max,, ),()*3600(
A
E
cascadeydroelectric plants:

HHG
NN
TNE)*3600(
j i
ijGNjDijHijjRAQHE
11
,,,,,,max,, ),(
jD
H,
er
ijGN
Q,,
nd no
igned
saved-watlevel armal generation flow of hy-
dro-driven generator iin plant j.
13) Inequality costraint fom
vel:
ijOijIjpHtxH ,,,,
),( 

(54)
5 Study Examples and Analysis
stem including
minimize the sum of the
w
ervoir inflow in each
ca
In this paper, Guangxi electric power sy
Hongshuihe hydroelectric stations in Hongshuihe river is
taken for a studying example. The data for Hongshuihe
hydroelectric plants and coal-fired electric plants in
Guangxi electric power system is shown in Table 1 and
Table 2 respectively. In the following section, three cases
are given to illustrate the component and factor analytic
method for optimal electric energy production of thermal
power systems in one hour.
According to the objective to
ater-consumed volume used for electric energy produc-
tion in 8 cascaded hydroelectric plants and the wa-
ter-consumed volume converted from coal-consumed
volume by 12 coal-fired plants, the plant with smaller
water-consumed volume or coal-water-consumed vol-
ume is the first one to be scheduled to generate. As
shown in Table 1 and 2, the plants with greater rated in-
stall capacity have smaller water-consumed volume or
coal to water volume in per unit electric energy output,
while the plants with smaller rated install capacity have
greater water-consumed volume or coal to water volume
in per unit electric energy output.
In high in-flow period, the res
scaded hydroelectric plant is assumed to be high. In
this case, the water flow and water volume for electric
energy production in each cascaded reservoir is available.
Because of much more available water flow for electric
energy production and smaller water-consumed volume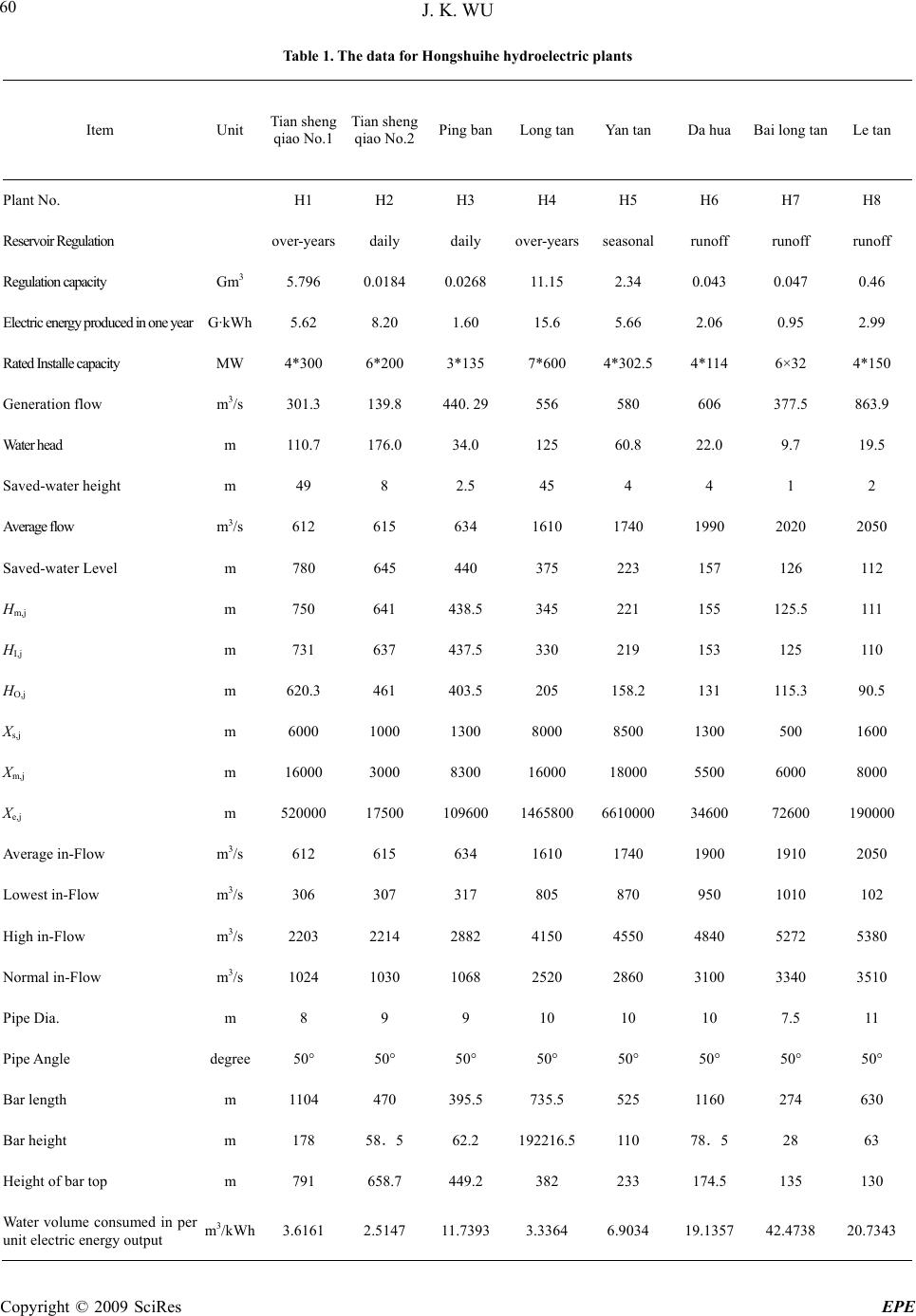

J. K. WU
60
gshu he hydroelectric plants
Item Unit
Tian sheng Tian sheng Ping banLong tanYan tan Da hua Bai long tanLe tan
Table 1. The data for Honi
qiao No.1 qiao No.2
Plant No. H1 H2 H3 H4 H5 H6 H7 H8
Reservoir Regulation overars daily daily overarsseasonalrunof runof runof
G3 5.0.0.
uced in one year G·kW
4*306*203*137*604*305 4*1 6×32 4*15
440.
m612 615 1610 1740 1990 2020 2050
Level
m,j 438. 125.
I,j
O,j 620. 1
s,j 1000 8000 8500 1300
m,j 1600160018006000
e,j 52001465 661034601900
m
2203 2214 2882 4150 4550 4840 5380
degr50° 50° 50° 50° 50°
1395. 735.1
58 578
top 449.135 130
med in per
unit electric energy output m3/kWh 3.6161 2.5147 11.7393 3.3364 6.9034 19.1357 42.4738 20.7343
-ye-yefff
Regulation capacity m796 0184 0268 11.15 2.34 0.043 0.047 0.46
Electric energy prodh 5.62 8.20 1.60 15.6 5.66 2.06 0.95 2.99
Rated Installe capacity MW 0 0 5 0 2.140
Generation flow m3/s 301.3 139.8 29 556 580 606 377.5 863.9
Water head m 110.7 176.0 34.0 125 60.8 22.0 9.7 19.5
Saved-water height m 49 8 2.5 45 4 4 1 2
Average flow 3/s 634
Saved-water m 780 645 440 375 223 157 126 112
H m 750 641 5 345 221 155 5 111
H m 731 637 437.5 330 219 153 125 110
H m 3 461 403.5 205 158.2 131 15.3 90.5
X m 6000 1300 500 1600
Xm 0 3000 8300 0 0 5500 8000
X m 00 17500 109600 8000000 72600 00
Average in-Flow3/s 612 615 634 1610 1740 1900 1910 2050
Lowest in-Flow m3/s 306 307 317 805 870 950 1010 102
High in-Flow m3/s 5272
Normal in-Flow m3/s 1024 1030 1068 2520 2860 3100 3340 3510
Pipe Dia. m 8 9 9 10 10 10 7.5 11
Pipe Angle ee 50° 50° 50°
Bar length m 104 470 5 5 525 160 274 630
Bar height m 178 ．5 62.2 192216.110 ．5 28 63
Height of barm 791 658.7 2 382 233 174.5
Water volume consu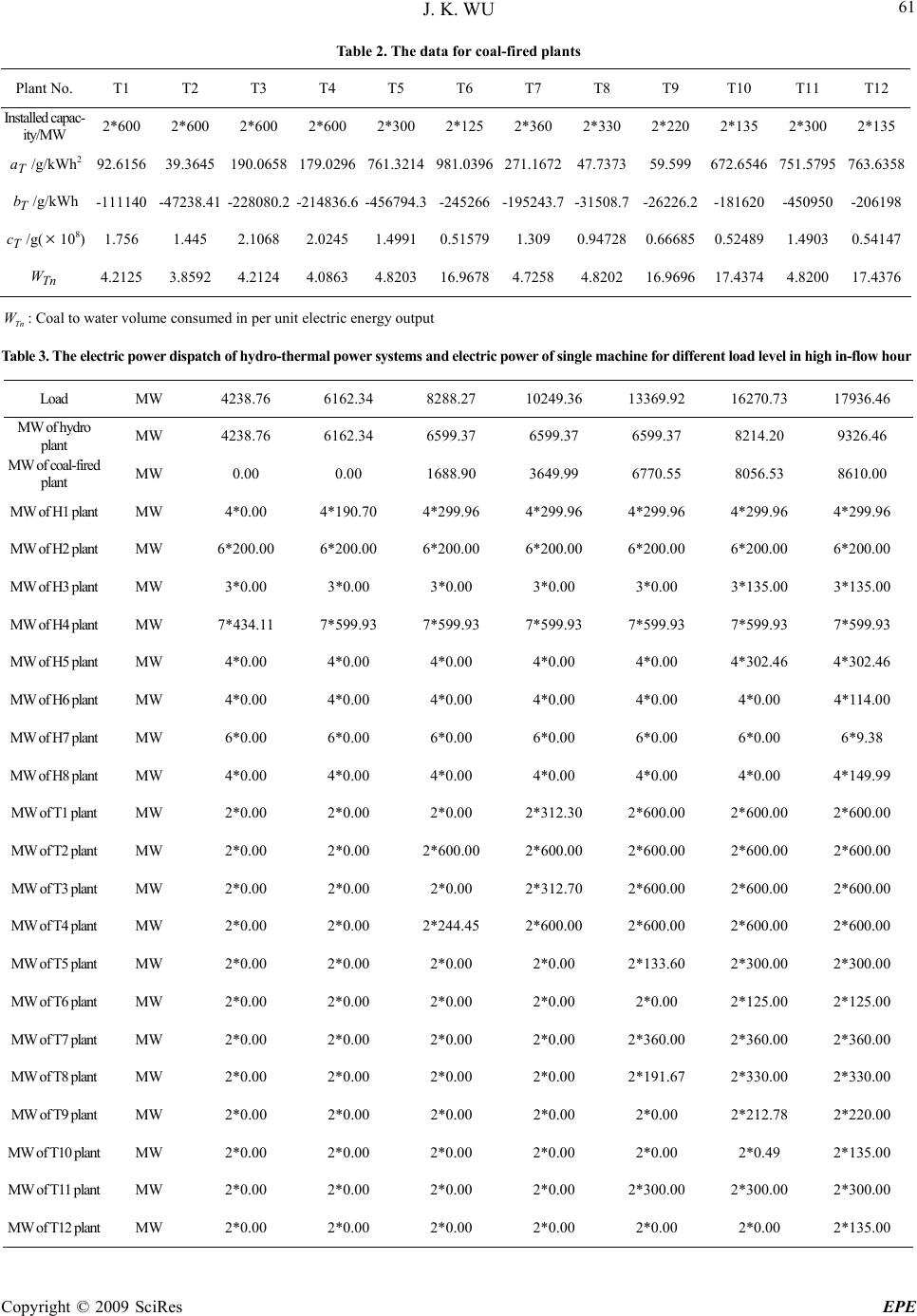

J. K. WU
61
Table 2. The data for coal-fired plants
T2 T3 T4 T5 T6 T7 T8 T9 T10 T11 T12
Plant No. T1
Installed capac-2*600 2*600 2*600 2*600 2*300 2*125 2*360 2*330 2*220 2*135 2*300 2*135
ity/MW
T
a/g/kWh
T/g/kW
292.6156 39.3645 190.0658 179.0296 761.3214 981.0396 271.167247.737359.599672.6546 751.5795 763.6358
h -111140 -47238.41 -228080.2 -214836.6 -456794.3-245266-195243.7-31508.7-26226.2 -181620 -450950-206198
/g( 1.756 1.445 2.1068 2.0245 1.49910.515791.309 0.947280.66685 0.52489 1.49030.54147
b
T
c108)
Tn
W 4.2125 3.8592 4.2124 4.0863 4.820316.96784.7258 4.820216.9696 17.4374 4.820017.4376
Tn
W: Coal to water volume consumed in per unit electric energy output
Table 3. The electric power dispatch of hydro-thermal power systems and electric power of single machine for different load level in high in-flow hour
Load MW 4238.76 6162.34 8288.27 10249.36 13369.92 16270.73 17936.46
MW of hydro MW 4238.76 6162.34 6599.37 6599.37 6599.37 8214.20 9326.46
plant
MW o MW 0.00 0.00 1688.90 3649.99 6770.55 8056.53 8610.00
MW 4*0.00 4*190.70 4*299.96 4*299.96 4*299.96 4*299.96 4*299.96
MWlant MW 6*200.00 6*200.00 6*200.00 6*200.00 6*200.00 6*200.00 6*200.00
MW of H5 plant MW 4*0.00 4*0.00 4*0.00 4*0.00 4*0.00 4*302.46 4*302.46
MW of H6 plant MW 4*0.00 4*0.00 4*0.00 4*0.00 4*0.00 4*0.00 4*114.00
MW of H7 plant MW 6*0.00 6*0.00 6*0.00 6*0.00 6*0.00 6*0.00 6*9.38
MW of H8 plant MW 4*0.00 4*0.00 4*0.00 4*0.00 4*0.00 4*0.00 4*149.99
MW of T1 plant MW 2*0.00 2*0.00 2*0.00 2*312.30 2*600.00 2*600.00 2*600.00
2*60 2*60
MW of T4 plant MW 2*0.00 2*0.00 2*244.45 2*600.00 2*600.00 2*600.00 2*600.00
MW of T5 plant MW 2*0.00 2*0.00 2*0.00 2*0.00 2*133.60 2*300.00 2*300.00
MW of T6 plant MW 2*0.00 2*0.00 2*0.00 2*0.00 2*0.00 2*125.00 2*125.00
MW of T7 plant MW 2*0.00 2*0.00 2*0.00 2*0.00 2*360.00 2*360.00 2*360.00
MW of T8 plant MW 2*0.00 2*0.00 2*0.00 2*0.00 2*191.67 2*330.00 2*330.00
MW of T10 plant MW 2*0.00 2*0.00 2*0.00 2*0.00 2*0.00 2*0.49 2*135.00
MW of T11 plant MW 2*0.00 2*0.00 2*0.00 2*0.00 2*300.00 2*300.00 2*300.00
MW of T12 plant MW 2*0.002*0.00 2*0.00 2*0.002*0.00 2*0.002*135.00
f coal-fired
plant
of H1 pMWlant
of H2 p
MW of H3 plant MW 3*0.00 3*0.00 3*0.00 3*0.00 3*0.00 3*135.00 3*135.00
MW of H4 plant MW 7*434.11 7*599.93 7*599.93 7*599.93 7*599.93 7*599.93 7*599.93
MW of T2 plant MW 2*0.00 2*0.00 0.00 2*600.00 0.00 2*600.00 2*600.00
MW of T3 plant MW 2*0.00 2*0.00 2*0.00 2*312.70 2*600.00 2*600.00 2*600.00
MW of T9 plant MW 2*0.00 2*0.00 2*0.00 2*0.00 2*0.00 2*212.78 2*220.00

J. K. WU
62
Tc energy productioo-thermr systems and energy comp hydro plantferent in high in-flowr
d M6162.31092 0.73 17
able 4. The electrin of hydral poweonent ofs for dif load level hou
LoaW4 249.36 13369.1627 936.46
Electric energy produced in T kWh6162340.00 10249360.00 13369920.00 16270730.00 17936460.00
T
E/percege 6162340.0.00659939 659936 821448 932600
16770480562 86100
Share of in ntage
Share of in ntage 2176
Share of in
6 7
nta kWh00/10366.45/64. 366.45/49.200.36/50. 460.00/52.
G
E/percentage kWh0.00/0.00 3649993.55/35.6553.55/50.6529.64/49.5000.00/48.0
1
fG E/perce kWh176170.75/2.8588 185478.51/2.8106185478.51/2.8106240112.90/2.9231 365469.36/3.9186
2
fG
E/perce kWh3.80/0.3532 24708.59/0.3744 24708.59/0.3744 45305.26/0.5515 82046.25/0.8797
Share of in /percentage
3
fG EkWh5265952.61/85.453 5609409.21/84.999 5609409.21/84.9997141210.74/86.937 8078269.18/86.616
46
/perage
f+
G
5
f+
cent
f
EkWh98452.84/11.334279770.13/11.8158 779770.13/11.8158787571.45/9.5879 800675.21/8.5850
in py output, the hydroelectric plants
have muchperiori r el
energy production than coal-fired plants when the load is
ifferent load level in high in-flow
ho
With increase in load, the percentage shared by hy-
increase
ic plants take
100% and coal-fired plants takes 0.
er unit electric energ
more suty to be scheduled foectric droelectric plants s, while the percentage
smaller. For example, when the load is 4238.76MW, the
hydroelectric plant H2 is first in full power output, and
plant H4 is for the remainder of the load; when the load
is 6162.34MW, H2 and H4 is first in full power output,
and H1 is for the remainder of the load, as shown in Ta-
ble 3. With increases in the load, the coal-fired plants
with smaller coal-water consumption volume are also
gradually put into schedule for electric energy produc-
tion till the load arrives at the sum of the rated install
capacity of all hydroelectric and coal-fired plants, as
shown in Table 3.
Table 4 shows the electric energy production of hy-
dro-thermal power systems and energy component of
hydro plants for d
ur. When the load is small, higher percentage of
electric energy production is shared by hydroelectric
plants than coal-fired plants, while lower percentage is
shared by hydroelectric plants than coal-fired plants,
as shown in Table 4. With increase in load, the percent-
age shared by hydroelectric plants increases, while the
percentage shared by coal-fired plants decreases, as
shown in Figure 2 and Figure 3. It is also seen that for a
load of about 7000MW of load, hydroelectric plants
take 100% and coal-fired plants takes 0.
shared by coal-fired plants decreases, as shown in
Figure 2 and Figure 3. It is also seen that for small
than about 7000MW of load, hydroelectr
00.5 11.5 2
x 10
4
40
50
60
70
80
90
100
Load/MW.
share of HE/%
igure 2. Sharing percentage of electric energy produced by hydro
plants (HE: Electric energy produced by hydro plants)
F
00.5 11.5 2
60
x 10
4
0
10
20
30
40
50
Load/MW .
Figure 3. Sharing percentage of electric energy pr
share of TE/%
oduced by
coal-fired plants(TE: Electric energy produced by hydro plants)
00.5 11.5 2
x 10
4
1.5
4
2
2.5
3
3.5
Load/M W.
share of DE/%
Figure 4. Sharing percentage of electric energy converted from
water-deep pressure energy (DE: Electric energy converted from
water-deep pressure energy)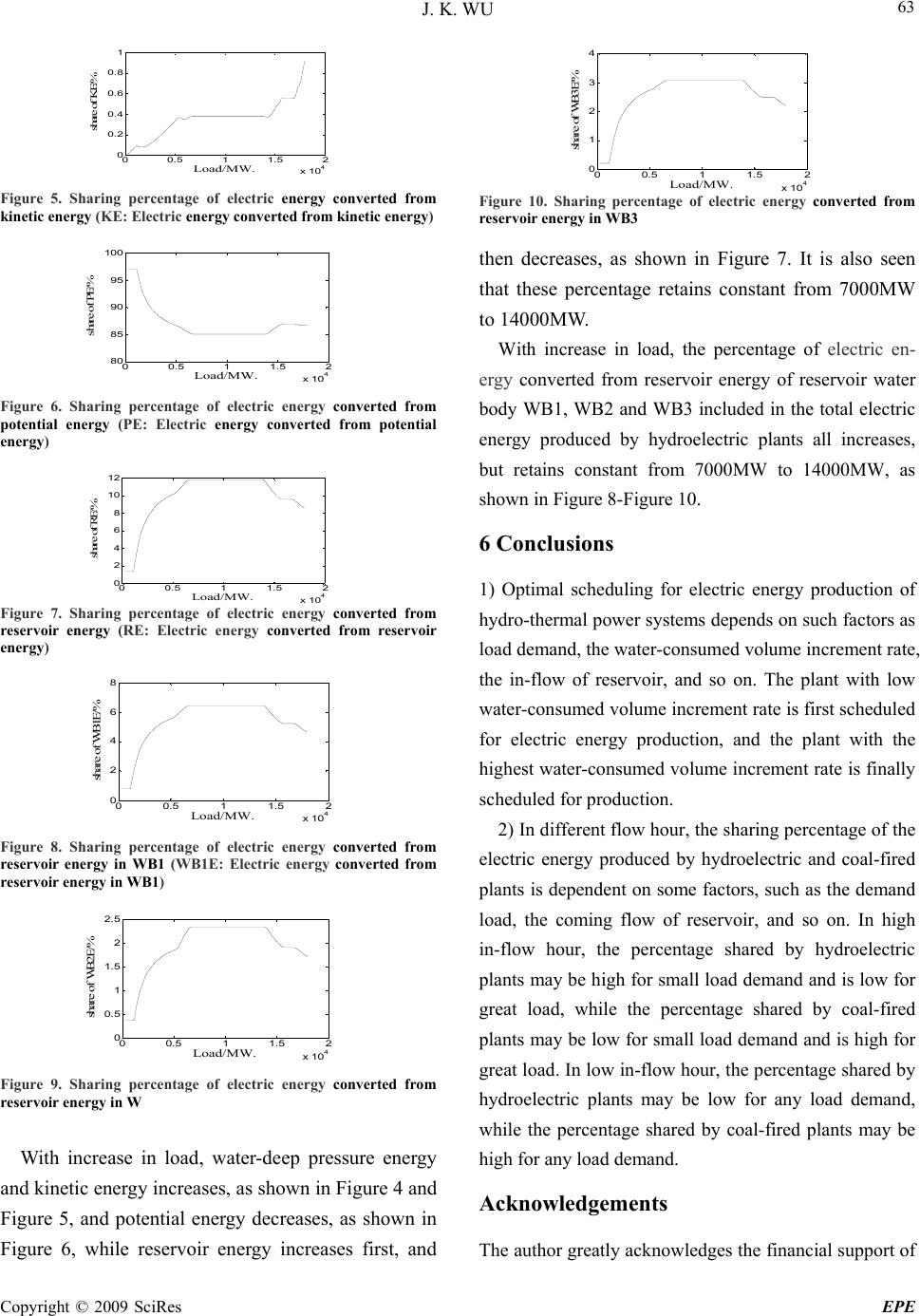

J. K. WU
63
00.5 11.5 2
x 10
4
0
0.2
0.4
0.6
0.8
1
Load/M W.
share of KE/%
Figure 5. Sharing percentage of electric energy coerted from nv
kinetic energy (KE: Electric energy converted from kinetic energy)
00.5 11.5 2
x 10
4
80
85
90
95
100
Load/MW.
share of PE/%
Figure 6. Sharing percentage of electric energy coom nverted fr
potential energy (PE: Electric energy converted from potential
energy)
00.5 11.5 2
x 10
4
0
2
4
6
8
10
12
Load/M W.
share of RE/%
Figure 7. Sharing percentage of electric energy converted from
reservoir energy (RE: Electric energy converted from reservoir
energy)
00.5 11.5 2
x 10
4
0
2
4
6
8
Load/MW.
share of WB1E/%
Figure 8. Sharing percentage of electric energy converted from
reservoir energy in WB1 (WB1E: Electric energy converted from
reservoir energy in WB1)
00.5 11.5 2
x 10
4
0
0.5
1
1.5
2
2.5
Load/MW.
share of WB2E/%
Figure 9. Sharing percentage of electric energy converted from
reservoir energy in W
00.5 11.5 2
x 10
4
0
1
2
3
4
Load/MW.
share of WB3E/%
Figure 10. Sharing percentage of electric energy converted from
then decreases, as shown in Figure 7. It is also seen
th
body WB1, WB2 and WB3 included in the total electric
energy produced by hydroelectric plants all increases,
but retains constant from 7000MW to 14000MW, as
shown in Figure 8-Figure 10.
1) Optimal scheduling for electric energy production of
eservoir, and so on. The plant with low
w
ydroelectric and coal-fired
on some factors, such as the demand
load, the coming flow of reservoir, and so on. In high
reservoir energy in WB3
at these percentage retains constant from 7000MW
to 14000MW.
With increase in load, the percentage of electric en-
ergy converted from reservoir energy of reservoir water
6 Conclusions
hydro-thermal power systems depends on such factors as
load demand, the water-consumed volume increment rate,
the in-flow of r
ater-consumed volume increment rate is first scheduled
for electric energy production, and the plant with the
highest water-consumed volume increment rate is finally
scheduled for production.
2) In different flow hour, the sharing percentage of the
electric energy produced by h
plants is dependent
in-flow hour, the percentage shared by hydroelectric
plants may be high for small load demand and is low for
great load, while the percentage shared by coal-fired
plants may be low for small load demand and is high for
great load. In low in-flow hour, the percentage shared by
hydroelectric plants may be low for any load demand,
while the percentage shared by coal-fired plants may be
high for any load demand.
With increase in load, water-deep pressure energy
and kinetic energy increases, as shown in Figure 4 and
Figure 5, and potential energy decreases, as shown in
Figure 6, while reservoir energy increases first, and
Acknowledgements
The author greatly acknowledges the financial support of

J. K. WU
64
vation Plan in Graduate Ed
llace S. W. and Fleten S. E., “Stochastic programming m
nergy,” The series Handbooks in Operations Research and
Management Science, Vol. 10, pp. 637-677, 2003.
., and Li C. A., “Scheduling hydro power
othermal coordination
ow
[10] Conejo A. J., Arroyo J. M., Contreras J., et al., “Self-scheduling
of a hydro producer in a pool-based electricity market,” IEEE
, et al., “Ex-
ixed integer programming ap-
Fast evolu-
haris J. B., et al., “A
., Ni E., and Li R., “An optimization-based algorithm for
aotic particle
2007.
rres G., and Zambroni de Souza A.
warm opti-
rothermal schedul-
pinning reserve through network flows,”
the National High Technology Research and Develop-
ment Program of China (863 Program) (2007AA04Z
197), National Natural Science Foundation of China
(50767001), Nature Science Foundation of Guangxi
(0640028), Program for 100 Young and Middle-aged
Disciplinary Leaders in Guangxi Higher Education In-
stitutions (RC20060808002), Science and Technology
Project of Guangxi Education Administration (200808
MS150) and Guangxi Innou-t
cation.
REFERENCES
[1] Fleten S. E., Wallace S. W., and Ziemba W. T., “Portfolio man-
agement in a deregulated hydropower based electricity market,”
In Proceedings of the 3rd International Conference on Hydro-
power Development, pp. 197-204, 1997.
[2] Fleten S. E., Wallace S. W., and Ziemba W. T., “Hedging elec-
tricity portfolios via stochastic programming,” IMA volumes on
Mathematics and Its Applications, Vol. 128, pp. 71-93, 2002.
[3] Ilyas Eker, “The design of robust multi-loop-cascaded hydro
governors,” Engineering Computer, Vol. 20, No. 2, pp. 45-53,
2004.
[4] Wa
in e
odels [17] Yu B. H., Yuan X. H., and Wang J. W., “Short-term hy-
dro-thermal scheduling using particle swarm optimization
method,” Energy Conversion and Management, Vol. 48, No. 7,
pp. 1902-1908,
[5] Guan X., Svoboda A [18]
systems with restricted operating zones and discharge ramping
constraints,” IEEE Transactions on Power System, Vol.14, No.1,
pp. 126-131, 1999.
[6] Yang J. S., and Chen N, “Short term hydr
C.,
using multipass dynamic programming,” IEEE Transactions on
Power System, Vol. 4, No. 3, pp. 1050-1056, 1989.
[7] Li C., Jap P., and Streiffert D, “Implementation of network fl
programming to the hydrothermal coordination in an energy
management system,” IEEE Transactions on Power System, Vol.
8, No. 3, pp. 1045-1053, 1993.
[8] Rosenthal R. E., “A nonlinear network flow algorithm for
maximization of benefits in a hydroelectric power system,” Op-
eration Research, Vol. 29, No. 4, pp. 763-786, 1981.
[9] Chang G. W., Aganagic M., Waight J. G., et al., “Experiences
with mixed integer linear programming based approaches on
short-term hydro scheduling,” IEEE Transactions on Power Sys-
tems, Vol. 16, No. 4, pp. 743-749, 2001.
Transactions on Power System, Vol. 17, No. 4, pp. 1265-1272,
2002.
[11] Chang G., Mohamed Aganagic W, Waight James G
periences with mixed integer linear programming based ap-
proaches on short-term hydro scheduling,” IEEE Transactions on
Power System, Vol. 16, No. 4, pp. 743-749, 2001.
[12] Nilsson O. and Sjelvgren D., “M
plied to short-term planning of a hydro-thermal system,” IEEE
Transactions on Power System, Vol. 11, No. 1, pp. 281-286, 1996.
[13] Sinha N., Chakrabarti R., and Chattopadhyay P. K., “
ionary programming techniques for short-term hydrothermal
scheduling,” Electric Power Systems Research, Vol. 66, pp.
97-103, 2003.
[14] Zoumas C. E., Bakirtzis A. G., Theoc
genetic algorithm solution approach to the hydrothermal coordi-
nation problem,” IEEE Transactions on Power System, Vol. 19,
No. 2, pp. 1356-1364, 2004.
[15] Guan X
scheduling hydrothermal power systems with cascaded reser-
voirs and discrete hydro constraints,” IEEE Transactions on
Power System, Vol. 12, No. 4, pp. 1775-1780, 1997.
[16] Jiang C. W. and Etorre B., “A self-adaptive ch
swarm algorithm for short term hydroelectric system scheduling
in deregulated environment,” Energy Conversion and Manage-
ment, Vol. 46, No. 17, pp. 2689-2696, 2005.
Umayal S. P. and Kamaraj N., “Stochastic multi objective
short term hydrothermal scheduling using particle swarm opti-
mization,” In Indicon Annual IEEE, pp. 497-501, 2005.
[19] Esmin A. A. A., Lambert-To
“A hybrid particle swarm optimization applied to loss power
minimization,” IEEE Transactions on Power System, Vol. 20, No.
2, pp. 855-859, 2005.
[20] Abido M. A., “Optimal power flow using particle s
mization,” Electrical Power Energy System, Vol. 24, pp.
563-571, 2002.
[21] Zambelli M., Siqueira T. G., Cicogna M., et al., “Deterministic
versus stochastic models for long term hyd
ing,” In Proceedings of IEEE Power Engineering Society Gen-
eral Meeting, 2006.
[22] Heredia F. J., Nabonal N. L., “Optimum short-term hydrother-
mal scheduling with s
IEEE Transactions on Power System, Vol. 10, No. 3, pp.
1642-1651, 1995.