Journal of Applied Mathematics and Physics
Vol.03 No.08(2015), Article ID:59118,7 pages
10.4236/jamp.2015.38129
Numerical Simulation of Freak Wave Generation in Irregular Wave Train
Lei Wang, Jinxuan Li*, Shuxue Li
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian, China
Email: *Lijx@dlut.edu.cn


Received 15 July 2015; accepted 19 August 2015; published 26 August 2015

ABSTRACT
In this paper, a numerical wave tank is developed based on High Order Spectral (HOS) method considering the wave-maker boundary. The 2D irregular wave trains are simulated for a long time by using this model. The freak wave is observed in the wave train, and its generation process is analyzed via wavelet analysis. The results show that the numerical tank can accurately simulate the wave generation and propagation, even for the freak wave. From the analysis of freak wave generation, it can be found that, two wave groups with different frequency components superpose together to form a large wave group. The large wave group modulation generates the freak wave.
Keywords:
Freak Wave, High Order Spectral Method, Numerical Wave Tank

1. Introduction
The freak wave (also called extreme wave, rouge wave) was defined as the wave whose height is more than twice the significant wave height, which represents the extreme oceanic conditions. It has larger wave height and stronger nonlinear, and can cause serious damage to the oceanic structures and ships. In recent years, as frequent human activities move towards the deep ocean, the harsh marine environment becomes a thread to oceanic engineering. Accurate estimation and understanding of severe extreme events are essential for human safety and for cost-effective design.
In the past years, many researchers paid attentions to the studies of freak wave [1]-[3]. Some mechanisms were presented to explain the generation of freak wave, such as, modulation instability (or Benjamin-Feir instability) [4] [5], wave focusing [6] [7], and wave-current or wave-wind interaction [8]-[10]. Based on these mechanisms, the freak wave was generated and studied through theoretical, experimental and numerical methods. The theoretical analysis was mainly based on modulation instability. Benjamin-Feir [11] found that the Stokes wave was unstable to small perturbations, and the unstable sideband components would grow exponentially. This phenomenon can be described by the nonlinear Schrödinger equation. Dysthe &Trulsen [12] and Osborne et al. [13] showed the breather solutions of nonlinear Schrödinger equation were considered as simple analytical models of freak waves.
There were many physical experiments on the generation of freak wave. Onorato et al. [14] [15] studied freak wave generation in long-crested sea conditions initialized as a JONSWAP spectrum. Li et al. [16] observed the generation process of freak wave in unstable irregular wave train and analyzed the freak wave based on wavelet analysis. Baldock et al. [17] investigated nonlinear surface water waves undertaken in 2-dimenional wave flume by a large number of water waves were focused at one point in space and specific time to produce a large transient wave group. Chin and Yao [18] investigated the influence of current on the freak wave generation in 2D wave flume.
Numerical model was also an important approach to study the freak wave generation and its hydrodynamics. It can solve the problem that in physical experiment, the length of the wave tank cannot satisfy requirement of the long-time evolution of wave surface. The most common method is based on nonlinear Schrödinger equation. Onorato et al. [19] studied freak wave generation in long-crested sea conditions based on the cubic nonlinear Schrödinger equation. While, the nonlinear Schrödinger equation is weak nonlinear equation, considering that the freak wave generation is strong nonlinear process, many fully nonlinear numerical models were developed. For example, Zhao et al. [20] simulated the freak wave generation based on VOF method. Yan and Ma [21] simulated the interaction of freak wave and wind using finite element method.
In order to deeply understand the freak wave generation, a numerical wave model based on High Order Spectral (HOS) method (Dommermuth and Yue [22]) is developed in this paper. Long-time irregular wave trains are generated and the freak wave is observed and analyzed. The method solves the derivative terms by Fast Fourier Transform (FFT) method. Compared with other methods, the spectral method has the properties of fast convergence and low computational cost. It is convenient to the long-time simulation.
2. Numerical Model
2.1. Governing Equations
It is assumed that the fluid is incompressible and inviscid, and the flow is irrotational. The velocity potential Φ(x, z, t) in the 2D fluid domain satisfies Laplace’s equation,
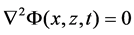 . (1)
. (1)
Following Zakharov [23], the fully nonlinear free surface boundary conditions can be expressed in terms of the velocity potential at the water surface as
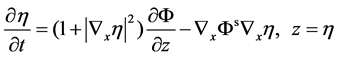 (2)
(2)
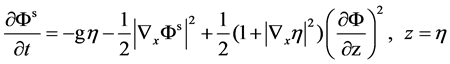 (3)
(3)
where Φs(x, t) = Φ(x, η, t) is the velocity potential on the water surface z = η.
On the fixed boundaries (the bottom, side and end walls of the tank), the conditions can be written simply as
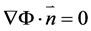 (4)
(4)
where 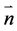 is a vector normal to the boundary considered.
is a vector normal to the boundary considered.
If the wave maker boundary is assigned to the left of the wave basin, the corresponding boundary condition can be written as
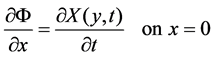 (5)
(5)
where X(t) is the displacement of the wave maker board.
2.2. Numerical Procedure
In order to solve this non-homogeneous problem, following Agnon and Bingham [24], the velocity potential can be split into the sum of a prescribed non-periodic components Φw and an unknown period component Φf, i.e.,
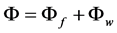 (6)
(6)
where the prescribed non-periodic components Φw satisfies the wave maker boundary condition (5) and other lateral boundary conditions (4). So, Equations (2) and (3) can be rewritten as follows:
 (7)
(7)
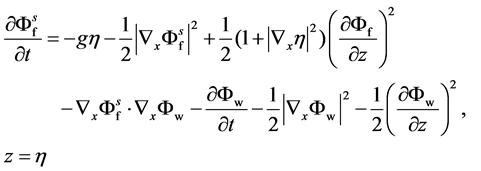 (8)
(8)
Therefore, determining Φw becomes the first key problem in establishing the numerical model using the HOS method. Different expansions can be used, such as, Agnon and Bingham [24] used polynomials in 2D wave tank simulation. Bonnefoy et al. [25] employed a spectral expansion in 2D and 3D wave tank simulation. In this paper, we use Bonnefoy’s method. The non-periodic components can be written as:
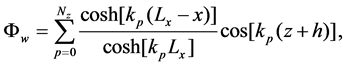 (9)
(9)
in which kp = (2p − 1)π/4h, h is water depth.
The unknown period component Φf satisfies the free surface Equations (2), (3) and lateral boundary condition (4). It can be solved by HOS method proposed by Dommermuth and Yue [22].
2.3. Verification of the Numerical Model
In order to verify the accuracy of the numerical model, the two-dimensional experimental focused wave data was used. The focused wave experiment was conducted in a two-dimensional wave flume. The focusing method was introduced in Li and Liu [26]. The two cases wave, with A = 0.03 m, f = 0.5 - 1.16 Hz, fc = 0.83 Hz and A = 0.06 m, f = 0.5 - 1.36 Hz, fc = 0.83 Hz, were adopted. The corresponding wave steepness kcA were 0.09 and 0.18, respectively. The waves were assumed to be focused at a distance 11.4m from the wave-maker. The NJS amplitude distribution was used, and the water depth was 0.5 m (kch = 1.54). The numerical wave tank is 40 m long. Figure 1 and Figure 2 present the comparisons of the numerical and experimental time histories of the wave at the focusing point. The figures show that the numerically simulated focused wave surfaces agree well with the experimental data. However, the numerical and experimental values of the focused wave amplitude are larger than the assumed amplitude because of the nonlinear wave evolution.
Figure 1. Comparison between experimental data (dotted) and numerical results (solid lines) for two-dimensional focused waves for the case with A = 0.03 m, f = 0.50 Hz - 1.16 Hz, fc = 0.83 Hz.
Figure 2. Comparison between experimental data (dotted) and numerical results (solid lines) for two-dimensional focused waves for the case with A = 0.06 m, f = 0.50 Hz - 1.16 Hz, fc = 0.83 Hz.
3. The Simulation of Freak Wave Generation in Random Trains
In this paper, long-time irregular wave trains are simulated to generate and observe the freak wave. The incident irregular waves are modeled by a superposition of regular waves with different frequencies with random phases. The frequency spectrum adopts the JONSWAP spectrum with the peak enhancement factorg = 3.3. The peak frequency is fp = 1.0 Hz. In order to avoid the numerical calculation instability owing to the wave breaking, the significant wave height of the wave train was adopted 0.037 m. The corresponding BFI value is 0.58. Although the value of BFI is moderate, the freak wave can be generated during long time simulation (see Li et al. [16]). The wave tank is 100 m long, and the water depth is 1.2 m.
From long time simulation, the freak wave occurrence can be observed. Figure 3 gives short segments of time series of wave surface elevation at different locations. The freak generation process can be observed from the figure. At the location near the wave-maker, there are no signs of freak wave. With the wave propagation, some large wave generates. At 29.45 m from the wave maker, owing to the modulation of wave group, these large waves focus together and form a freak wave. The freak wave is similar to the typical form of “New Year Wave”. After the location 29.45 m, the freak wave disappears, these waves are dispersed and the number of wave in group increases. Comparing to physical experiment, the long distance evolution of freak wave can be conveniently observed in the numerical model simulation.
In order to analyze the process of freak wave generation, the evolution of the wavelet energy spectra at selected positions from the wave-maker is shown in Figure 4. In the figure, thesurfaceelevationofthewavesisshownbythewhitecurvesuperimposedontheenergyisolines.Two successive wave groups are seen at 9.0 m from the wave-maker. A group with comparatively low-frequency components is lagging behind the group with high- frequency components. Then, at the 19 m location, the group with low-frequency components, travelling at greater speed, is merging with the higher-frequency group. At 29.45 m from the wave-maker, owing to the modulation of wave group, the freak wave occurs, the wavelet spectrum isolines show an almost symmetrical triangular form and higher-frequency components and higher energy values are evident, indicative of stronger nonlinear interactions at the time of the freak wave generation. Then, at 50 m to 60 m from the wave-maker, the surfaces begin the group demodulation, the wavelet spectra show that the low-frequency component is at the front of the wave group.
4. Conclusion
In order to deeply understand the freak wave generation, a 2D numerical wave tank is developed based on high order spectral method considering the non-periodic boundary condition in this paper. Long time irregular wave simulation is conducted. The freak wave generation process is analyzed by wavelet analysis. The simulation results show that the numerical model is valid to simulate the freak waves. From the process of freak wave generation in the simulation, it can be found that, two wave groups with different frequency components superpose together to form a large wave group. The large wave group modulation generates the freak wave.
Figure 3. The time series of wave surface elevation at different locations.
Figure 4. Wavelet energy spectra at different distances.
Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grant Nos. 51309050, 51221961 and 51179028). Their supports are gratefully acknowledged.
Cite this paper
Lei Wang,Jinxuan Li,Shuxue Li, (2015) Numerical Simulation of Freak Wave Generation in Irregular Wave Train. Journal of Applied Mathematics and Physics,03,1044-1050. doi: 10.4236/jamp.2015.38129
References
- 1. Kharif, C. and Pelinovsky, E. (2003) Physical Mechanisms of the Rogue Wave Phenomenon. European Journal of Mechanics—B/Fluids, 22, 603-634. http://dx.doi.org/10.1016/j.euromechflu.2003.09.002
- 2. Dysthe, K., Krogstad, H.E. and Muller, P. (2008) Oceanic Roguewaves. Annu. Rev. Fluid Mech., 40, 287-310. http://dx.doi.org/10.1146/annurev.fluid.40.111406.102203
- 3. Slunyaev, A., Didenkulova, I. and Pelinovsky, E. (2011) Roguewaters. Contemp. Phys., 52, 571-590. http://dx.doi.org/10.1080/00107514.2011.613256
- 4. Janssen, P. (2003) Nonlinear Four-Wave Interaction and Freak Waves. J Phys Oceanogr, 22, 863-884. http://dx.doi.org/10.1175/1520-0485(2003)33<863:NFIAFW>2.0.CO;2
- 5. Clamond, D. and Grue, J. (2002) Interaction between Envelope Solitons as a Model for Freak Wave Formations. Part I: Long Time Interaction. C R Mec, 330, 575-580. http://dx.doi.org/10.1016/S1631-0721(02)01496-1
- 6. Johannessen, T. and Swan, C. (2001) A Laboratory Study of the Focusing of Transient and Directionally Spread Surface Water Waves. Philos Trans R SocLond, Ser A, 457, 971-1006. http://dx.doi.org/10.1098/rspa.2000.0702
- 7. Liu, S. and Hong, K. (2005) Physical Investigation of Directional Wave Focusing and Breaking Waves in Wave Basin. China Ocean Eng, 19, 21-35.
- 8. Hjelmervi, K.B. and Trulsen, K. (2009) Freak Wave Statistics on Collinear Currents. Journal of Fluid Mechanics, 637, 267-284. http://dx.doi.org/10.1017/S0022112009990607
- 9. Toffoli, A., Cavaleri, L., Babanin, A.V., Benoit, M., Bitn-er-Gregersen, E.M., Monbaliu, J., Onorato, M., Osborne, A.R. and Stansberg, C.T. (2011) Occurrence of Extreme Waves in Three-Dimensional Mechanically Generated Wave Fields Propagating over an Oblique Current. Natural Hazards and Earth System Sciences, 11, 895-903. http://dx.doi.org/10.5194/nhess-11-895-2011
- 10. Kharif, C., Giovanangeli, J.P., Touboul, J., Grare, L. and Pelinovsky, E. (2008) Influence of Wind on Extreme Wave Events: Experimental and Numerical Approaches. Journal of Fluid Mechanics, 594, 209-247. http://dx.doi.org/10.1017/S0022112007009019
- 11. Benjamin, T.B. and Feir, J.E. (1967) The Disintegration of Wa-vetrains on Deep Water. Part 1: Theory. J. Fluid Mech., 27, 417-430. http://dx.doi.org/10.1017/S002211206700045X
- 12. Dysthe, K.B. and Trulsen, K. (1999) Note on Breather Type Solutions of the NLS as a Model for Freak Waves. Physica Scripta, T82, 48-52. http://dx.doi.org/10.1238/Physica.Topical.082a00048
- 13. Osborne, A.R., Onorato, M. and Serio, M. (2000) The Nonlinear Dynamics of Rogue Waves and Holes in Deep-Water Gravity Wave Train. Phys. Letters A, 275, 386-393. http://dx.doi.org/10.1016/S0375-9601(00)00575-2
- 14. Onorato, M., Osborne, A.R., Serio, M. and Cavaleri, L. (2005) Modulational Instability and Non-Gaussian Statistics in Experimental Random Water-Wave Trains. Physics of Fluids, 17, Article ID: 078101. http://dx.doi.org/10.1063/1.1946769
- 15. Onorato, M., Osborne, A.R., Serio, M., Cavaleri, L., Brandini, C. and Stansberg, C.T. (2004) Observation of Strongly Non-Gaussian Statistics for Random Sea Surface Gravity Waves in Wave Flume Experiments. Phys Rev E, 70, Article ID: 067302. http://dx.doi.org/10.1103/physreve.70.067302
- 16. Li, J., Yang, J., Liu, S. and Ji, X. (2015) Wave Groupiness Analysis of the Process of 2D Freak Wave Generation in Random Wave Trains. Ocean Engineering, 104, 480-488. http://dx.doi.org/10.1016/j.oceaneng.2015.05.034
- 17. Baldock, T., Swan, C. and Taylor, P. (1996) A Laboratory Study of Nonlinear Surface Waves on Water. Philos. Roy. Soc. London, 452A, 649-676. http://dx.doi.org/10.1098/rsta.1996.0022
- 18. Chin, H. and Yao, A. (2004) Laboratory Measurement of Limiting Freak Waves on Currents. Journal of Geophysical Research, 109, Article ID: C12002.
- 19. Onorato, M., Osborne, A.R., Serio, M. and Bertone, S. (2001) Freak Waves in Random Oceanic Sea States. Phys Rev Lett, 86, 5831-5834. http://dx.doi.org/10.1103/PhysRevLett.86.5831
- 20. Zhao, X.Z., Hu, C.H. and Sun, Z.C. (2010) Numerical Simulation of Extreme Wave Generation Using VOF Method. Journal of Hydrodynamics, 22, 466-477. http://dx.doi.org/10.1016/S1001-6058(09)60078-0
- 21. Yan, S. and Ma, Q.W. (2010) Numerical Simulation of Interaction between Wind 2D Freak Waves. European Journal of Mechanics, B/Fluids, 29, 18-31. http://dx.doi.org/10.1016/j.euromechflu.2009.08.001
- 22. Dommermuth, D.G. and Yue, D.K.P. (1987) A High-Order Spectral Method for the Study of Nonlinear Gravity Waves. Journal Fluid Mechanics, 184, 267-288. http://dx.doi.org/10.1017/S002211208700288X
- 23. Zakharov, V.E. (1968) Stability of Periodic Waves of Finite Am-plitude on the Surface of a Deep Fluid. J. Appl. Mech. Tech. Phys, 9, 190-194 (English Transl.). http://dx.doi.org/10.1007/BF00913182
- 24. Agnon, Y. and Bingham, H. (1999) A Non-Periodic Spectral Method with Application to Nonlinear Water Waves. European Journal Mech. B/Fluids, 18, 527-534. http://dx.doi.org/10.1016/S0997-7546(99)80047-8
- 25. Bonnefoy, F., Touzé, D. and Le Ferrant, P. (2004) Generation of Fully-Nonlinear Prescribed Wave Fields Using a High-Order Spectral Model. Proc. 14th International Offshore and Polar Engineering Conference, Toulon.
- 26. Li, J. and Liu, S. (2015) Foused Wave Properties Based on a High Order Spectral Method with a Non-Periodic Boundary. China Ocean Engineering, 29, 1-16. http://dx.doi.org/10.1007/s13344-015-0001-7
NOTES
*Corresponding author.











