Journal of Applied Mathematics and Physics
Vol.03 No.08(2015), Article ID:59109,7 pages
10.4236/jamp.2015.38123
DEM Simulations of Granular Soils under Undrained Triaxial Compression and Plane Strain
Guobin Gong
Department of Civil Engineering, Xi’an Jiaotong-Liverpool University (XJTLU), Suzhou, China
Email: guobin.gong@xjtlu.edu.cn


Received 3 May 2015; accepted 19 August 2015; published 26 August 2015

ABSTRACT
The paper presents 3D DEM simulation results of undrained tests for loose assemblies with varied porosities under both triaxial compression and plane strain conditions, using a periodic cell. The undrained tests were modelled by deforming the samples under constant volume conditions, which corresponds to saturated soil samples. The undrained stress paths are shown to be qualitatively similar to physical experimental results. The triggering of liquefaction and temporary liquefaction is identified by a microscopic parameter with redundancy factor (RF) equal to unity, which defines the transition from “solid-like” to “liquid-like” behaviour. The undrained behaviour of granular soils is found to be mainly governed by the evolution of redundancy factor, and a reversal of deviatoric stress in stress path (temporary liquefaction) is found to be due to temporary loss of contacts forming a structural mechanism in the system where RF is smaller than unity during the evolution.
Keywords:
DEM, Periodic Cell, Saturated, Undrained, Liquefaction, Coordination Number, Redundancy Factor

1. Introduction
Interest in undrained behaviour especially for loose sand has received much attention since the pioneering experimental work [1] [2], but the undrained behavior of loose sand (especially liquefaction) has not been well explained. The traditional analysis of the undrained response of soils has been mainly based on a continuum model, where the microscopic structures at grain scales are usually inappropriately ignored. The Discrete Element Method (DEM) provides an ideal tool to examine the micromechanics of granular materials such as sand. DEM was originally developed in [3] for the analysis of rock mechanics problems. In DEM, a sample consists of discrete particles, which only interact at particle contacts. The particles can rotate, slide and separate. With such a particulate system, DEM is particularly suitable for modelling granular media.
Most DEM simulations are performed “in a vacuum” without fluid, as were done in this paper. The undrained behaviour was modeled using 2D DEM by [4]-[7] among others. Most of these researchers use 2D constant volume simulations for mimicking undrained saturated soil tests, except that both constant volume and coupled fluid-particle interaction methods are used in [6] [7]. The comparison of undrained behaviour using constant volume and fluid-particle interaction methods showed no difference essentially as indicated [6] [7]. Of all the above researchers, temporary liquefaction is observed only in [6] [7]. It should be noted that the undrained condition modeled by constant volume method is only suitable for saturated soil samples, not for unsaturated samples. The paper presents results of 3D DEM simulations under both undrained (constant volume) triaxial compression (UTC) and undrained plane strain (UPS) conditions and a comparision is made. A micromechanical description of liquefaction and the related phenomena are focused.
2. Simulation Details
Three-dimensional DEM simulations have been performed on poly disperse systems of 3600 elastic spheres using the same TRUBAL code as used in [8]. Contact interactions are calculated using algorithms based on the theories of Hertz (normal interaction) and Mindlin and Deresiewicz (tangential interaction), see [9] [10]. The Young’s modulus and Poisson’s ratio for each particle were specified as E = 70 GPa and n = 0.3, respectively. During the shear stage, the interparticle friction coefficient was set to μ = 0.5. Nine different sizes of spheres were used: 0.25 mm (2), 0.26 mm (20), 0.27 mm (220), 0.28 mm (870), 0.29 mm (1376), 0.30 mm (870), 0.31 mm (220), 0.32 mm (20), 0.33 mm (2), with an average particle diameter of
All the undrained simulations reported in the paper were carried out in a periodic cell. A periodic cell allows a particle that moves out of the cell to be re-mapped back into the cell at a corresponding location on the opposite face. The particle that moves out of the cell carrys all the same information as that moving into the cell, except for particle positions. An infinite lattice can be imagined by replicating one cell throughout space. Thus, the simulation can be performed free from boundaries. More information about periodic cell can be found in [13]. To mimic undrained conditions, constant volume with strain control mode is used. For the undrained triaxial compression simulations, the specified strain-rates in the three principal strain directions were set to 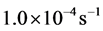 (compression),
(compression), 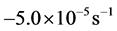 and
and 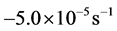 (extension) respectively. For the undrained plane strain simulations, the specified strain-rates in the three principal strain directions were set to
(extension) respectively. For the undrained plane strain simulations, the specified strain-rates in the three principal strain directions were set to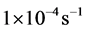 , 0 and
, 0 and 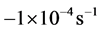 respectively. All the simulations start from an initial stress state that is almost isotropic with all the normal (principal) stresses approximately equal to 100 kPa.
respectively. All the simulations start from an initial stress state that is almost isotropic with all the normal (principal) stresses approximately equal to 100 kPa.
During the simulations, the ensemble average stress tensor is calculated (see [14]) as follows,
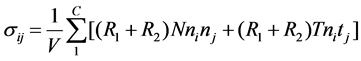 (1)
(1)
where the summations are over the C contacts in the volume V, R1 and R2 are the radii of the two spheres in contact, N and T are the magnitudes of the normal and tangential contact forces at the contact, ni is the unit vector normal to the contact plane and ti is the unit vector parallel to the contact plane.
3. Results and Discussions
In this section, results are presented of undrained test simulations on all the samples and both the macroscopic and microscopic behaviouris discussed. The macroscopic behaviour is presented in terms of stress path and deviatoric stress. The microscopic behaviour is presented in terms of redundancy factor.
3.1. Macroscopic Behaviour
Figure 1 and Figure 2 showed eviatoric stress (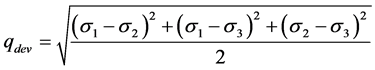 , for triaxial com- pression, this degenerates to deviator stress
, for triaxial com- pression, this degenerates to deviator stress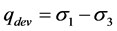 ) plotted against mean effective stress for all the loose
) plotted against mean effective stress for all the loose
Figure 1. Stress path under UTC [n refers to porosity].
Figure 2. Stress path under UPS.
systems under undrained (constant volume) triaxial compression (UTC) and undrained plane strain (UPS) conditions respectively. It can be seen from the Figures that the overall trends of the stress path are not much different for the two types of strain conditions. In both cases, all the loose sample exhibits an initial increase of p’ except the loosest sample (n = 0.425). However, the loose sample (porosity, n = 0.405) does not exhibit a reversal under UPS, as it does under UTC. This indicates that the undrained behaviour is much related to strain conditions. The reason for this difference could be explained microscopically as explained later.
Figure 3 and Figure 4 show the evolution of the deviatoric stress plotted against deviatoric strain (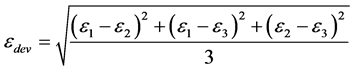 ) for all the loose systems under UTC and UPS respectively. It can be
) for all the loose systems under UTC and UPS respectively. It can be
seen from both the figures that for the three very loose samples (n = 0.425, n = 0.419, n = 0.414), the initial peak of deviatoric stress occurs at small strains, followed by gradual decrease (with sharpest drop for the loosest sam- ple in each strain condition, but the drop in UPS is less sharp than in UTC), and with further straining the
Figure 3. Evolution of deviatoric stress under UTC.
Figure 4. Evolution of deviatoric stress under UPS.
devaitoric stress becomes more or less constant at small values (called steady state in [15]). Such behaviour of the very loose samples is called liquefaction in soil mechanics literature [15]. It can also be seen from both the figures that for the three medium loose samples, the initial peak deviatoric stress occurs at relatively larger strain compared with that for the three very loose samples except that the medium loose sample (n = 0.405) does not exhibit an initial peak under UPS. Similar to that of the very loose sample, the initial peak for the medium loose samples (except the sample with n = 0.405 under UPS) is followed by a gradual decrease with further straining until a “steady” state is obtained. Such a “steady” state is, however, only temporary for the medium loose samples, called quasi-steady state [16], and with further straining the deviatoric stress goes up again. Such behaviour of the medium loose samples is also called temporary or partial liquefaction in soil mechanics. Both Figure 3 and Figure 4 show that liquefaction occurs for the very loose samples (n = 0.414, n = 0.419, n = 0.425), and temporary liquefaction occurs for medium loose samples except for the sample (n = 0.405) under UPS. It can be concluded that the undrained behaviour is dependent on porosity (strength decreases with increase of porosity) and strain conditions (UPS is more resistant to liquefaction/temporary liquefaction).
3.2. Microscopic Behaviour
In this section, microscopic description of undrained behaviour in terms of redundancy factor is presented, and the triggering of liquefaction/temporary liquefaction is identified by such a microscopic parameter with the value of unity. Both triaxial compression and plane strain simulation results are presented and compared.
For a granular assembly with spherical particles with a finite value of friction at the contacts, a microscopic parameter termed redundancy factor (RF) is defined [17] [18] as follows,
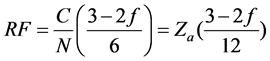 (2)
(2)
where f is the fraction of sliding contacts and the average coordination number is defined as the ratio of twice number of contacts and number of particles, i.e.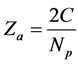 . If RF > 1 then we have a redundant system and the
. If RF > 1 then we have a redundant system and the
system can be said to be solid-like, and for IR < 1 we have a structural mechanism and the system can be said to be liquid-like. Therefore, RF = 1 defines a limit phase transition condition from solid-like to liquid-like behaviour.
For the six systems examined, the evolutions of redundancy factor are plotted in Figure 5 and Figure 6 respectively, rationally indicating when liquefaction, RF < 1, initiates. In both figures, the horizontal line with
Figure 5. Evolution of redundancy factor under UTC.
Figure 6. Evolution of redundancy factor under UPS.
RF = 1 defines a phase transition from solid-like (non-liquefied) behaviour to liquid-like (liquefied or temporarily liquefied) behaviour. It can be seen that the three very loose samples do not re-establish solid-like behaviour after they drop below the phase transition line, indicating liquefaction. The medium loose samples (except the sample n = 0.405 under UPS) generally first drop below the phase transition line, and then go up until they get close to or even cross the phase transition line, indicating temporary liquefaction. In both figures, the initial intersection points of the phase trasnsition line and evolution of RF curves indicate the onset of liquefaction or temporary liquefaction. It can be easily seen that a looser sample liquefies earlier in each strain condition (UTC or UPS). Interestingly, in Figure 6 the sample (n = 0.405) lies in the solid-like region during all the evolution (or negative “liquefied degree” at any strain range), and this guarantees the system has enough enduring contacts that keep the system stable, therefore, no stress reversal at macroscopic level is observed for the sample (n = 0.405) under UPS, see macroscopic behaviour in Figure 2 and Figure 4. On the contrary, in Figure 5 the sample (n = 0.405) stays in the solid-like region mostly except when the deviatoric strain is between 0.06 and 0.08, where liquid-like behaviour occurs. This small range of liquid-like region, causes the system (n = 0.405) to become a structural mechanism transiently under UTC, which leads to the quick drop of deviatoric stress. Subsequently, the system regains contacts and becomes robust again, and therefore reversal of stress is observed macroscopically for the sample (n = 0.405) as shown in Figure 1 and Figure 3.
Figure 7 shows comparison of evolution of redundancy factor under UTC and UPS, where it can be seen that the RF value under UPS is generally above that under UTC for a given deviatoric strain for all the samples except the very loose samples (n = 0.419, n = 0.414) at relatively larger strain where liquefaction already occurs. Allowing for this deviation, it can be said that due to the restraint of one of the principal directions, the system under UPS becomes more robust and has more enduring contacts than that under UTC, which could also be inferred the sample (n = 0.405) under UPS does not have a stress reversal while the same system under UTC has a stress reversal as discussed above.
4. Conclusions
A micromechanical formula for defining the triggering of soil liquefaction (temporary liquefaction) is established in terms of redundancy factor. The relation among redundancy factor, average coordination number and percentage of sliding contacts is provided. The evolution of redundancy factor is provided under undrained axisymmetric compression and plane strain conditions and compared. A phase transition is associated with redundancy factor of unity, which defines the transition from solid-like behaviour to liquid-like behaviour. This phase transition corresponds to a limit average coordination number slightly in excess of four. From comparision of simulation results under two types of strain conditions, it is found that:
Figure 7. Comparison of evolution of redundancy factor under UTC and UPS.
1) A reversal of deviatoric stress in stress path under undrained conditions is due to the fact that the system becomes a structural mechanism (RF < 1) during part of the evolution. If RF > 1 during all the evolution, the reversal does not occur.
2) A system under undrained plane strain is generally more robust in resisting liquefaction than under UTC.
Acknowledgements
The authors acknowledge the funding by the Engineering and Physical Sciences Research Council, UK (Grant No.GR/R91588) for the work reported in the paper. The authors would also like to thank Prof. Andrew Chan from Federation University Australia and Dr. Colin Thornton from University of Birmingham UK, for their guidance and discussion on the relevant work.
Cite this paper
Guobin Gong, (2015) DEM Simulations of Granular Soils under Undrained Triaxial Compression and Plane Strain. Journal of Applied Mathematics and Physics,03,1003-1009. doi: 10.4236/jamp.2015.38123
References
- 1. Bishop, A.W. (1966) The Strength of Soils as Engineering Materials. Sixth Rankine Lecture. Geotechnique, 16, 89- 130. http://dx.doi.org/10.1680/geot.1966.16.2.91
- 2. Castro, G. (1969) Liquefaction of Sands. Soil Mechanics Series No. 81, Harvard Univ., Cambridge.
- 3. Cundall, P.A. (1971) A Computer Model for Simulating Progressive, Large-Scale Movements in Blocky Rock Systems. Proc. Symp. Int. Soc. Rock Mech., 2, 2-8.
- 4. Thornton, C. and Barnes, D.J. (1986) Com-puter Simulated Deformation of Compact Granular Assemblies. Acta Mechanica, 64, 45-61. http://dx.doi.org/10.1007/BF01180097
- 5. Ng, T.-T. and Dobry, R. (1994) Numerical Simulations of Monotonic and Cyclic Loading of Granular Soil. Journal of Geotechnical Engineering, ASCE, 120, 388-403. http://dx.doi.org/10.1061/(ASCE)0733-9410(1994)120:2(388)
- 6. Bonilla, R.R.O. (2004) Numerical Simulations of Undrained Granular Media. Ph.D. Thesis, University of Waterloo, Canada.
- 7. Shafipour, R. and Soroush, A. (2008) Fluid Coupled-DEM Modelling of Undrained Behaviour of Granular Media. Computers and Geotechnics, 35, 673-685. http://dx.doi.org/10.1016/j.compgeo.2007.12.003
- 8. Thornton, C. (2000) Numerical Simulations of Deviatoric Shear Deformation of Granular Media. Geotechnique, 50, 43-53. http://dx.doi.org/10.1680/geot.2000.50.1.43
- 9. Mindlin, R.D. and Deresiewicz, H. (1953) Elastic Spheres in Contact under Varying Oblique Force. Trans. ASME, J. Appl. Mech. 20, 327-344.
- 10. Thornton, C. (1999) Interparticle Relationships between Forces and Displacements. In: Oda, M. and Iwashita, K., Eds., Mechanics of Granular Materials—An Introduction, Balkema, Rotterdam, 207-217.
- 11. Thornton, C. and Randall, C.W. (1988) Applications of Theoretical Contact Mechanics to Solid Particle System Simulation. In: Satake and Jenkins, Eds., Micromechanics of Granular Materials, Elsevier, Amsterdam, 133-142.
- 12. Gong, G. (2008) DEM Simulations of Drained and Undrained Behaviour. Ph.D. Thesis, University of Birmingham, UK.
- 13. Cundall, P.A. (1988) Computer Simulations of Dense Sphere Assemblies. In: Satake and Jenkins, Eds., Micromechanics of Granular Materials, Elsevier, Amsterdam, 113-123. http://dx.doi.org/10.1016/b978-0-444-70523-5.50021-7
- 14. Thornton, C. and Zhang, L. (2010) On the Evolution of Stress and Microstructure during General 3D Deviatoric Straining of Granular Media. Geotechnique, 60, 333-341. http://dx.doi.org/10.1680/geot.2010.60.5.333
- 15. Poulos, S.J. (1981) The Steady State of Deformation. Journal of Geotechnical Engineering, ASCE, 17, 553-562.
- 16. Alarcon-Guzman, A., Leonards, G.A. and Chameau, J.L. (1988) Un-drained Monotonic and Cyclic Strength of Sand. Journal of Geotechnical Engineering, ASCE, 114, 1089-1109. http://dx.doi.org/10.1061/(ASCE)0733-9410(1988)114:10(1089)
- 17. Gong, G., Zha, X. and Wan, C. (2012) A Microscopic Definition of Liquefaction for Sand. International Conference on Structural Computation and Geotechnical Mechanics, Procedia Earth and Planetary Science, 5, 140-145. http://dx.doi.org/10.1016/j.proeps.2012.01.024
- 18. Gong, G., Lin, P., Qin, Y. and Wei, J. (2012) DEM Simulation of Liquefaction for Granular Media under Undrained Axisymmetric Compression and Plane Strain Conditions. Acta Mechanica Solida Sinica, 25, 562-570. http://dx.doi.org/10.1016/S0894-9166(12)60051-2








