Journal of Applied Mathematics and Physics
Vol.03 No.08(2015), Article ID:59106,8 pages
10.4236/jamp.2015.38121
Development and Application of Two-Dimensional Numerical Model on Shallow Water Flows Using Finite Volume Method
Szu-Hsien Peng1,2, Chuan Tang2
1Department of Spatial Design, Chienkuo Technology University, Changhua City, Taiwan
2State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu, China
Email: shpeng@cc.ctu.edu.tw, tangc707@gmail.com


Received 10 June 2015; accepted 19 August 2015; published 26 August 2015

ABSTRACT
This present study develops a 2-D numerical scheme to simulate the velocity and depth on the actual terrain by using shallow water equations. The computational approach uses the HLL scheme as a basic building block, treats the bottom slope by lateralizing the momentum flux, then refines the scheme using the Strang splitting to deal with the frictional source term. Besides, a decoupled algorithm is also adopted to compute the aggradation and degradation of bed-level elevation by using the Manning-Strickler formula and Exner’s relationship. The main purpose is to set up the window interface of 2-D numerical model and increase the realization of engineers on these characteristics of hydraulic treatment and maintenance.
Keywords:
Shallow Water Equations, Finite Volume Method, Hydraulic Treatment and Maintenance

1. Introduction
Many hazards caused by typhoons in Taiwan have resulted in large damages or pecuniary loss in recent years. The function of local drainage in urban or rural regions usually plays an important role in the task of controlling floods. The detention facility is one of the usual methods to control floods in stream planning. The present research presents a two-dimensional numerical model, DBFVM-2D, which is developed by using the shallow water equations and finite volume method to assess the function of detention facility. The shallow water equations are derived from the Navier-Stokes Equations by depth-averaged integration in vertical direction.
In consideration of frequent flood disasters in Taiwan, hydraulic engineering or drainage system planning need more efficient or accurate hydraulic analyses. Besides, a numerical model is used for inputting disaster conditions for computing the possible flood range before the flood disaster prevention and response operation plan so as to predict possible financial losses or personnel injuries and precede various solutions and strategies with images and other disaster prevention and response data analyses.
Meanwhile, the protected disaster scale should be preset before planning the flood disaster prevention and response operation, and the numerical model inputs related disaster conditions for computing the possible flood range and estimating possible flood range and depth. Based on above disaster scale settings, possible financial losses or personnel injuries therefore could be predicted, and various solutions and strategies are preceded with images and other disaster prevention and response data analyses. It is regarded as the objective of flood disaster potential development.
In the planning of soil and water conservation for slope land development, the runoff increased by watershed sediment getting in the river course or development behaviors could be controlled the sediment or discharge through various soil and water conservation constructions, such as groundsill works, detention basins, and settling basins. Engineers used to precede plan and design according to empirical formula; a numerical model for the situation simulation of allocated equipment could help understand the hydraulic characteristics in order to review the plan and design being played.
Dam-break caused by floods or earthquakes or sudden opening of gates could result in surges on the river flow which are delivered towards downstream. The use of a high-resolution numerical method in 2D shallow water equations to solve surges has been studied in four categories of numerical methods. For instance, MacCormack numerical method and the explicit scheme of Finite Differential Method (FDM) were employed to simulate 2D wave propagations by Garcia & Kahawital and Fennema & Chaudhry; Akanbi & Katopodes applied Finite Element Method (FEM) to simulate flood waves; and, Katopodes & Stelkoff simulated 2D dam-break flows with Method of Characteristics (MOC) [1]-[4].
This study aims to develop a 2D numerical model, in which shallow water equations are regarded as the governing equation and Finite Volume Method is applied to develop user-friendly window interface. Comparing to other numerical methods, Finite Volume Method presents the following advantages:
It could apply irregular grids in Finite Element that it is applicable to various irregular landforms.
Finite Volume Method would discretize conservative differential equations.
The calculation speed of Finite Volume Method equals to Finite Differential Method, but is faster than Finite Element Method that it could reduce large computing time.
Conservative equations of flow continuity and momentum are proceeded integration discretization, when the conservative characteristics are remained, i.e. keeping the conservative properties of some physical quantity, so that it is easier to analyze the flow of discontinuity like seismic waves.
Commonly used inundation models contain 1D steady flow or unsteady flow inundation model, quasi 2D inundation model (or cell model), and 2D inundation model (including Block-Street Network Inundation Model, SOBEK Model, and FLO-2D Model). Each inundation model presents the advantages and disadvantages and generally requires expensive license fee.
Finite Volume Method therefore is utilized for establishing a 2D numerical model and developing the user- friendly window interface by regarding shallow water equations as the governing equation in the present paper. The model covers the functions of dam-break flow, flood inundation simulation, and bed sediment load transport calculation, which could be applied to the hydraulic calculation of groundsill works and detention basins. Moreover, the uncoupled mode is used for calculating the bed load, and sediment continuity equations could simulate the bed scour and deposition. They are beneficial to the application of project planning.
2. Mathematical Model
2.1. Governing Equations
For homogeneous and incompressible flow, the Navier-Stokes equations in a Cartesian coordinate system could be denoted as [3]
Continuity equation:
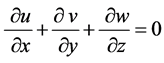 . (1)
. (1)
Momentum equation:
x direction
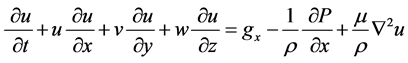 . (2)
. (2)
y direction
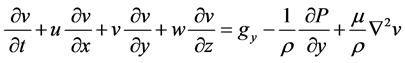 . (3)
. (3)
z direction
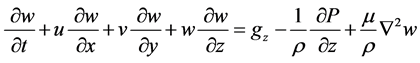 . (4)
. (4)
where x, y , z are the coordinate axes of the Cartesian coordinate system, t is the time, u ,v, w are the components of flow velocity at x, y, z directions, 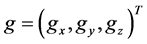 is the weight of unit mass, P is the flow pressure, r is the fluid density, μ is the dynamic viscosity, and
is the weight of unit mass, P is the flow pressure, r is the fluid density, μ is the dynamic viscosity, and 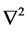 is a Laplace operator, i.e.
is a Laplace operator, i.e.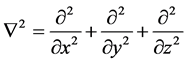 .
.
Preceding the flow depth integration of above equations, the depth-averaged equation could be acquired to derive the following shallow water equations [3]:
Continuity equation:
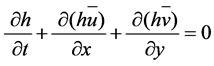 . (5)
. (5)
Momentum equation of water depth-averaged at x direction
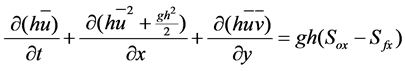 . (6)
. (6)
Momentum equation of water depth-averaged at y direction
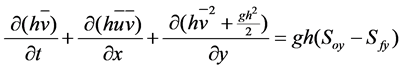 . (7)
. (7)
And energy slope
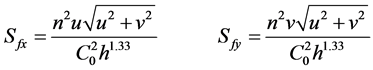 . (8)
. (8)
where n is the Manning coefficient, C0 = 1 (for SI unit), and C0 = 1.49 (for imperial unit).
2.2. Numerical Scheme
Explicit uniform grid discretization governing equations in Finite Volume Method are applied to the numerical method, and the Godunov-type scheme is used for solving Riemann problem [5]. The numerical flux is calculated with the HLL scheme, which is used for dealing with non-conservative terms covering the bottom slope [6]. Finally, the Strang splitting is utilized for calculating the frictional source term [7]. The application of conservative Finite Volume Method separates the hyperbolic term and the source term in differential equations that the numerical model could be largely improved. For example, to envelop 1D grid to 2D grid, Dimensional Splitting is used for calculating x-sweeps, which are further used for calculating y-sweeps [8]. Similarly, The Strang splitting is also applied to calculate the bed shear stress. In each time step, the hyperbolic term in shallow water equations is first calculated which is regarded as the initial condition to calculate the friction.
Furthermore, the uncoupled mode is utilized for calculating the bed sediment of hyper concentrated flow. In the beginning (t = 0), the bed-level elevation is assumed known and the relative flow parameters could be acquired by solving shallow water equations, when the sediment transport is not taken into account. Such flow parameters are further used for calculating the bed sediment load of each grid, whose in/out sediment is used for estimating the scour and deposition of each grid. The sediment continuity equation is further utilized for calculating the bed-level elevation:
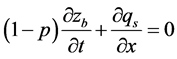 . (9)
. (9)
where p is the bed porosity, zb the bed-level elevation, and qs the volumetric sediment load of per unit width. A new bed profile (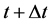 ) is then calculated, and the sediment calculation could be acquired by repeating the steps [9].
) is then calculated, and the sediment calculation could be acquired by repeating the steps [9].
Three bed sediment load equations of Schoklitsch, Meyer-Peter et al., and Einstein sediment load are currently used in this study [9], and the empirical formula for the power function of flow velocity is taken into consideration, where the coefficient and the power could be set by the user. To prevent the program from discretization caused by large changes of bed, the model could be set the relatively maximum variation allowance 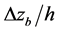 by the user. When the change exceeds the limit, the set value is the vertical variance. Meanwhile, the following equation is used for calculating the final vertical variance
by the user. When the change exceeds the limit, the set value is the vertical variance. Meanwhile, the following equation is used for calculating the final vertical variance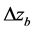 :
:
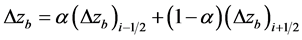 . (10)
. (10)
where 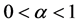 is regarded as a weighting factor, which appears in between backward difference and forward difference [10], and the central difference appears at
is regarded as a weighting factor, which appears in between backward difference and forward difference [10], and the central difference appears at
3. Results
3.1. Simulation of Asymmetric Dam-Break Flow
Assuming a 200 m × 200 m plane for the simulation, where an asymmetric opening with the width 75 m is in the middle, Figure 1. The water level at dam front is 10 m, while it shows 5 m, 0.1 m, and dry bed at dam back. The Manning n is assumed 0.15 and the boundary condition is assumed with closed walls to simulate the grids sized 5 m × 5 m and 2 m × 2 m. The simulation time is 7.2 sec, and Figure 2 shows the dam-break flow. Finite Volume Method is used for the Riemann discontinuity in this study that the downstream, even though it is a dry bed, could be well calculated, without being diverged.
3.2. Simulation of Dam-Break Flow Passing Square Column
The simulation area is a 1.6 m (L) × 0.6 m (W) closed channel, where a 0.12 m × 0.12 m square column is placed in the middle at x = 0.9 m; an initial depth 0.3 m appears before x = 0.4 m and the downstream depth 0.01 m to simulate the 2 cm × 2 cm grid with the Manning n 0.01 and the simulation time 2 sec. The results are shown in Figure 3. Although it is merely a 2D model, when comparing to the 3D model FLOW-3D, some important information could be acquired, but the calculation efficiency is much higher than it of the 3D model.
Figure 1. Simulation area of the asymmetric dam-break flow.




Figure 2. Simulation results of the asymmetric dam-break flow. (a) Initial states: upstream depth = 10 m; downstream depth = 5 m, 0.1 m, and dry bed (from left to right); (b) t = 7.2 sec for grid 5 m × 5 m; (c) t = 7.2 sec for grid 2 m × 2 m; (d) Previous study (Source: Liang et al., 2006 [11]).
3.3. Simulation of Retrogressive Erosion
The retrogressive erosion simulation assumes the channel bed profile suddenly appears rapid changes. The simulation data are acquired from the literature [12]. The experimental tank presents the length 15.8 m, the width 1.2 m, and the slope 0.00125, in which a








Figure 3. Simulation results of dam-break flow passing a square column. (a) t = 0 sec: side view and top view using FLOW- 3D (left); side view and top view using DBFVM-2D (right); (b) t = 0.31 sec: side view and top view using FLOW-3D (left); side view and top view using DBFVM-2D (right); (c) t = 0.8 sec: side view and top view using FLOW-3D (left); side view and top view using DBFVM-2D (right); (d) t = 1.34 sec: side view and top view using FLOW-3D (left); side view and top view using DBFVM-2D (right); (e) t = 1.97 sec: side view and top view using FLOW-3D (left); side view and top view using DBFVM-2D (right).
Figure 4. Simulation results of retrogressive erosion (experimental data measured by Bhallamudi & Chaudhry [12]).
4. Conclusion
The functions of the developed model contain dam-break flow, flood inundation simulation, and bed load sediment transport calculation, which could be applied to the hydraulic calculation of groundsill works and detention facilities. Besides, the uncoupled mode is utilized for calculating the bed load, and sediment continuity equations are applied to simulate the bed scour and deposition. Moreover, all programming codes in the numerical model are self-developed that they present high expandability. Meanwhile, Finite Volume Method is utilized for computing the model that it could effectively calculate the surges of dam-break flow. Connecting the uncoupled mode with sediment continuity equations and calculating the bed sediment load with the bed scour and deposition could assist engineers in modifying the construction design.
Acknowledgements
The paper was supported in part by the Ministry of Science and Technology, Taiwan (NSC 98-2622-B-270-001- CC3) and Opening fund of State Key Laboratory of Geohazard Prevention and Geoenvironment Protection at Chengdu University of Technology (SKLGP2013K008).
Cite this paper
Szu-Hsien Peng,Chuan Tang, (2015) Development and Application of Two-Dimensional Numerical Model on Shallow Water Flows Using Finite Volume Method. Journal of Applied Mathematics and Physics,03,989-996. doi: 10.4236/jamp.2015.38121
References
- 1. Fennema, R.J. and Chaudhry, M.H. (1989) Implicit Methods for Two-Dimensional Unsteady Free-Surface Flows. Jour. of Hydraulic Research, International Assoc. for Hydraulic Research, 27, 321-332. http://dx.doi.org/10.1080/00221688909499167
- 2. Fennema, R.J. and Chaudhry, M.H. (1990) Explicit Methods for Two-Dimensional Unsteady Free-Surface Flows. Jour. Hydraulic Engineering, Amer. Soc. of Civil Engrs., 116, 1013-1034. http://dx.doi.org/10.1061/(ASCE)0733-9429(1990)116:8(1013)
- 3. Chaudhry, M.H. (1993) Open-Channel Flow. Prentice-Hall, Inc., Englewood Cliffs.
- 4. Jonsson, P., Jonsén, P., Andreasson, P., Lundstr?m, T. and Hellstr?m, J. (2015) Modelling Dam Break Evolution over a Wet Bed with Smoothed Particle Hydrodynamics: A Parameter Study. Engineering, 7, 248-260. http://dx.doi.org/10.4236/eng.2015.75022�
- 5. Harten, A., Lax, P.D. and van Leer, B. (1983) On Upstream Difference and Godunov-Type Schemes for Hyperbolic Conservation Laws. SIAM Review, 25, 35-61. http://dx.doi.org/10.1137/1025002
- 6. Fraccarollo, L., Capart, H. and Zech, Y. (2003) A Godunov Method for the Computation of Erosional Shallow Water Transients. Int. J. Numer. Meth. Fluids, 41, 951-976. http://dx.doi.org/10.1002/fld.475
- 7. Fraccarollo, L. and Toro, E.F. (1995) Experimental and Numerical Assessment of the Shallow Water Model for Two- Dimensional Dam-Break Type Problems. J. Hydr. Res., 33, 843-864. http://dx.doi.org/10.1080/00221689509498555
- 8. Leveque, R.J. (2002) Finite Volume Methods for Hyperbolic Problems. Cambridge Univ. Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511791253
- 9. Graf, W.H. (1998) Fluvial Hydraulics. John Wiley & Sons, Chiche-ster.
- 10. Julien, P.Y. (2002) River Mechanics. Cambridge Univ. Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139164016
- 11. Liang, D., Falconer, R.A. and Lin, B. (2006) Comparison between TVD-MacCormack and ADI-Type Solvers of the Shallow Water Equations. Advances in Water Resources, 29, 1833-1845. http://dx.doi.org/10.1016/j.advwatres.2006.01.005
- 12. Bhallamudi, S.M. and Chaudhry, M.H. (1991) Numerical Modeling of Aggradation and Degradation in Alluvial Channels. J. Hydr. Engng., 117, 1145-1164. http://dx.doi.org/10.1061/(ASCE)0733-9429(1991)117:9(1145)



























