Received 8 June 2015; accepted 19 August 2015; published 26 August 2015

ABSTRACT

In this research, using the energy approach, a generalized dynamic model is derived for Galfenol (Iron-Gallium Alloy) based on the mechanical strain theory and the Jiles-Atherton model. Experiments have been conducted to measure the relationship between the strain and the magnetic field. Using experimental data, unknown parameters in the model have been identified by a developed optimization algorithm. Results show that the novel dynamic model with identified parameters is capable of describing the performance of the Galfenol rod. Simulation and experiment dynamic responses of Galfenol rods are derived. The simulation and the experiment both agree that the magnitude of the strain output decreases with the increase of the excitation frequency.

Keywords:

Galfenol, Transducer, Dynamics, Magnetostrictive Material, Magnetization Model

1. Introduction

With the advancement of high precision engineering, smart materials have attracted a lot of attention in decades. Currently, there are several favourite smart materials: shape memory alloy, piezoelectric material and traditional magnetostrictive materials (Metaglass 2605SC and Terfenol-D). Although the above listed materials have been employed in versatile applications, either the geometry complexity or the brittle nature prevents these materials from further applications. The research status starts to change upon the arrival of a novel magnetostrictive material, Galfenol, which is an alloy of iron and gallium. The high tensile strength and the high Currie temperature allow this material to work in harsh environment. Beyond that, Galfenol has an excellent machinability [1] that increases this material’s popularity, especially in miniature applications. In addition, Galfenol can be used with a simple configuration and assembly, because Galfenol does not need a pre-stress mechanism which benefits from the built-in anisotropic behaviour through the stress annealing process of Galfenol.

For the future design and control of Galfenol transducers, a generalized dynamic model for the design and control of Galfenol transducers is significantly required. For the motion control purpose, Braghin, Cinquemani and Resta [2] introduce a linear model for magnetostrictive transducers which is valid in the frequency range within. However, this model is built using the linear magnetomechanical equations which cannot predict the nonlinear hysteresis behaviour of Galfenol transducers. Meanwhile, efforts have been made to model the hysteresis behaviour of magnetostrictive materials. One of the most prevalent and earliest models is the Preisach model [3]. The Preisach model is a pure mathematical model which lacks of physical information. Another novel model is the Armstrong model [4] which is prevalently used to model Galfenol. Armstrong model acquires the final response by the microscopic analysis that requires a large amount of computation even for simple geometrical structures. On the other hand, it is hard to incorporate extra physical energy terms in the model, especially when the material is employed in a complicated system. More recently, a framework [5] based on the first and second laws of thermodynamics was developed to describe the hysteresis behaviour of the magnetostrictive material. It assumes that hysteresis results from domain changes that were modelled by the elementary hysteron. Another model for the magnetostrictive material is the Jiles-Atherton magnetization model [6]. In the earlier research, the domain rotation and the domain wall pinning were put in place to account for the energy loss caused by the hysteresis while the modelling of anhysteretic magnetization was based on the Langevin equation. Since the Jiles-Atherton magnetization model is based on physics, not only this model can interpret the response of Galfenol under the excitation, but also it can be easily modified by adding additional energy terms to describe additional physical effects. This feature leaves room for further modifications based on specific applications. Recently, the Jiles-Atherton model [7] has been applied to the ferromagnetic and the magnetostrictive materials. However, this model has not been applied in the modelling of Galfenol yet.

It’s an universal way to analyse multi-physics problems with energy approach which renders researchers the ability to model transducers from an overall perspective. Thus, the objective of this paper is to present a generalized dynamic model of Galfenol for longitudinal magnetostrictive transducers using the energy approach. The Jiles-Atherton model is applied to describe the hysteresis behaviour of Galfenol. The newly developed model is capable of describing the inherent nonlinear behaviour. Experiments have been conducted for the characterization and the validation of the new model. The unknown parameters from the Jiles-Atherton model have been identified using the experimental data.

2. Modeling

2.1. Dynamic Modelling Using Energy Approach

The sketch, Figure 1, simplified axial-deformation applications of Galfenol. The parameter 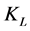denotes the stiffness of a spring, the parameter 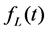is used to model a time-variant external forces applied on the system, and the accessories’ equivalent mass and the system’s structural damping are modelled as 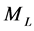and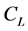, respectively. Under the assumption that this system is scleronomous, Galfenol is modelled as a continuous rod in the scheme. For Galfenol materials, an appropriate pres-tress can enlarge the final strain output significantly. However, Galfenol can be developed with a built-in stress using the stress annealing process to avoid the redundant pre-stress mechanism. In this modelling, the possible pre-stress is considered for the general application purpose. Pre-stress and amplification mechanisms in the system are modelled as an equivalent linear spring. The equations of motion are derived from the Hamilton’s principle,

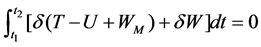(1)

where 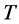is the kinetic energy, 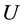is the strain energy, 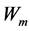is the magnetic energy, and is the work done by the external force. For the Galfenol rod, the relationships between strain, stress and magnetostriction are formulated as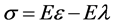. The parameter 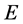is the Young’s modulus of Galfenol.

According to Figure 1, energy terms in the Hamilton’s principle are expressed as,

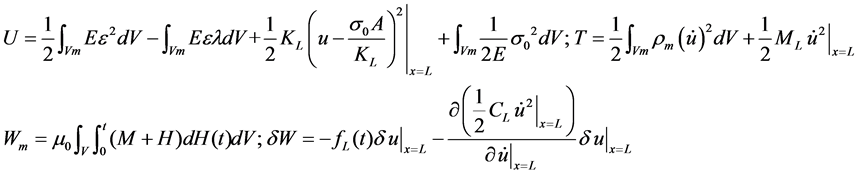(2)

In the above equations, 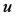is the mechanical deformation of the Galfenol rod, 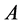is the cross-sectional area of the Galfenol rod, is the material’s density, is the pre-stress, and is the permeability of vacuum. The parameter and represent the magnetization and the magnetic field strength. Applying expressions of the above energy terms into Equation (1), the equations of motion can be written as,

(3)

with boundary conditions of

(4)

and initial conditions of

(5)

2.2. Model of Magnetization Hysteresis

The Jiles-Atherton model, a physical-based model for the magnetization, models the magnetization hysteresis as a function of domain rotation and wall pinning. Because the Jiles-Atherton model is a physical-based model with limited parameters, redundant experiments are not needed for the identification. This model is expanded into the following equations [8],

(6)

where is the local anhysteretic magnetization, represents the irreversible magnetization, is the domain interactions coefficient, is the reversibility coefficient, and the constant is the hysteresis loss co- efficient. The parameter is defined as 1 when and as −1 when. The parameter is the saturation magnetization, characterizes the shape parameter, and denotes the effective field. The energy input is represented by. Integrating over, the magnetization energy is derived. In a similar way, the hysteresis loss is obtained by integrating the irreversible magnetization,

(7)

The energy method is used to derive the relationship between the magnetization and the applied magnetic field. For Galfenol materials, the energy loss due to the eddy-current cannot be omitted. Based on the law of electromagnetic induction, the eddy current power loss per volume is derived as [9]. The term assumes an uniform distribution of the magnetic flux density for materials with low permeability. For materials with high permeability, it is inaccurate to directly assume that the magnetic flux density distributes uniformly within materials. Thus, in order to describe the behaviour of Galfenol that has a relatively high permeability, a correction coefficient is introduced to the classic eddy-current loss term to compensate the inaccuracy of the assumption. Then, the eddy-current loss can be written as

where is the diameter of rod, is the resistivity, is the geometry factor. For the system, the following energy equation [8] is satisfied,

(8)

Combining Equations (6) and (8), the magnetization M is numerically obtained. According to the quadratic moment domain rotation model [10], the relationship between the magnetization and the magnetostriction is modeled as follows,

(9)

where is the saturation magnetostriction.

The equations are solved for the relationship between Galfenol’s displacement and the applied magnetic field. The Jiles-Atherton model is used to describe the magnetization process within the Galfenol rod. As this model is first employed on Galfenol, five typical parameters of the Jiles-Atherton model are unidentified at this stage. Also, the energy loss related to the eddy-current also brings a correction parameter. In order to employ the built model in practical applications, these unknown parameters are to be identified. For this highly nonlinear system, the simulated annealing algorithm [11] has been developed to find the solution. In the developed algorithm, the

strain output of Galfenol has a certain function with respect to parameters, which is represented by . The error is defined as, where represents the experimental data and is the simulation result based on the current parameter set. In the following process, the nonlinear least-square algorithm is used to acquire the optimal solution.

3. Experimental Design

In the previous section, a generalized model for Galfenol has been built and the solution is provided. It is necessary to develop and conduct experiments for the characterization and the validation of this model. The stress annealed Galfenol sample () for this research is provided by ETREMA PRODUCTS.

Figure 2 shows the compact design for experiments. A reciprocating output is generated by providing an alternating current to the excitation coil surrounding the Galfenol rod. According to the Ampere’s circuital law, the relationship between the current and the magnetic field can be acquired. To achieve the largest energy efficiency, two end caps are used to ensure that the magnetic field distributes axially within the Galfenol rod. The assembled belleville spring and the set screw allow for the fine adjustment of the pre-stress. However, because the sample is stress annealed, there is no pre-stress applied to Galfenol in this experiment. An internal halting ring is employed to locate entire components. A housing is fabricated to offer protection for the Galfenol rod from the ambient disturbance. To prevent the generation of the eddy-current, the housing is grooved along the axial direction. Furthermore, to make the magnetic reluctance as small as possible, all parts of the assembly

are made of stainless steel. According to the manufacturer, Galfenol is capable of generating a strain output up to. In this design, the mass of the output rod is negligible compared to the stiffness of the system and there is no external force applied. Thus, the end mass, the structural damping, and the external force in Equation (2) are assumed to be zeros.

Harmonic current without bias is applied to the driving coil using a current amplifier (LA220) whose power is supplied by ST-1 Regulated Power Supply (Power Output 60 W). The following instruments are employed to evaluate the response of the Galfenol rod. First, the output displacement of the Galfenol rod is measured using the laser unit with the modulus of Polytec OFV534F. The modulus of the controller is OFV5000 that measures the displacement of the output rod’s top surface in micro-scale. The resolution chosen for this measurement is. The bandwidth of the laser unit for the displacement mode is from DC to which covers the frequency range of the measurement. Second, a current probe (Tektronix TCP0030) is used to measure the exact current that is supplied by the amplifier. Finally, signal outputs from these sensors are acquired and processed by the Tecktronix DPO 3014 oscilloscope. Figure 3 shows the described experimental scheme.

4. Results and Discussion

The Galfenol rod chosen for this test has a diameter of and a length of. The experiment was conducted at frequencies ranging from to. Figure 4 shows experimental results of the strain output versus the magnetic field under the quasi-static condition. The general trend of the Galfenol sample is that this material begins to reach saturation when the magnetic field is larger than. The nonlinear behaviours, both hysteresis and saturation, are exhibited by the experimental result. It is noticed that the hysteresis of the response increases with the rising of the excitation frequency. Physically, there is an explanation for the increased severity of hysteresis. The increasing frequency of the applied magnetic field leads to the generation of a larger eddy-current which results in a much severer hysteresis.

The parameter identification process were conducted based on the previously described algorithm. The experimental response under the excitation frequency of was used to derive parameters by fitting the model to the experimental data. The experimental data whose frequency equals to was selected to identify the eddy-current loss correction coefficient. The fitting result and the material property in the fitting are listed in Table 1.

Table 1. Material properties and fitted parameters.

Figure 5 shows the comparison between the simulated result and the experimental result at various excitation frequencies. The horizontal axis indicates the alternating of the applied magnetic field strength while the vertical axis shows the strain output of the rod. Nonlinear behaviours, e.g. the quadratic behaviour, the hysteresis, and the saturation, are characterized by this model. The quadratic behaviour reveals that the deformation of the Galfenol rod only relates to the strength of the applied magnetic field. The hysteresis behaviour and the energy dissipation by the eddy-current are explicitly observed. When the excitation frequency is, the response rarely exhibits hysteresis. With the increase of the excitation frequency, the hysteresis becomes severer. While the frequency is, the hysteresis becomes distinct for the system. The built model accurately describes the influence of the eddy-current on the hysteresis of Galfenol. Experimental and model responses in the time domain are shown in Figure 6. In addition, the frequency analysis is conducted on the model response and the experimental response of the Galfenol rod, as shown in Figure 7. It is noted that the model accurately describes frequency components of experimental results. It is also disclosed that discrepancies between model results and experimental results gradually become slightly larger with the rising of the excitation frequency. This could be because the model is built based on the amendatory classic eddy-current loss. Although a correction coefficient is introduced to account for the non-uniform distribution of the magnetic flux density, it is not precise enough for the high-precision application of Galfenol.

Simulation and model results of the dynamic response are plotted in Figure 8. The horizontal axis represents the excitation frequency of the Galfenol. The solid blue curve and the blue dashed curve reveal the model frequency response and the experimental frequency response of the Galfenol rod (), respectively. The red curves exhibit frequency responses of the Galfenol rod (). The build model can describe the dynamic response of the material. Both strain outputs of Galfenol rods show a decline trend along with the rising of the frequency due to the eddy-current. It should be noticed that when the diameter of Galfenol is reduced, the strain output ability of Galfenol is weakened because of the enlarged equivalent boundary spring stiffness (). This phenomenon also shows that the built model is able to describe the mechanical behaviour of Galfenol. Also, when the frequency increases, strain outputs of Galfenol rod () decrease significantly. Meanwhile, the Galfenol rod () does not show a strong decline trend. It indicates that Galfenol has a strong potential to be utilized in the development of vibrators with miniature sizes.

The purpose of this work is to provide a generalized model that is used for the subsequent design and control of Galfenol transducers. The correction coefficient in the model can be conveniently modified based on the experimental data for specific applications. For the precision application, the accuracy of the model can be improved by deriving the distribution of the magnetic flux density based on the Maxwell equations. Instead of using the eddy-current power loss term, a more precise model result can be derived employing the specific distribution of the magnetic flux density.

The experiment was conducted at frequencies ranging from. When the excitation frequency is larger than, the response of the experiment is too small due to the increased energy consumption by the eddy-current. Not only the reduced response will lead to the decreased signal to noise ratio in measurement, but also the response is meaningless to transducers. Theoretically, the verification of the model at higher frequencies can be conducted using smaller samples.

5. Conclusion

In this paper, a generalized dynamic model of Galfenol for longitudinal magneostrictive transducers is developed. The equations of motion are derived for Galfenol rods using the energy approach. This approach enables transducers to be analyzed from the macro perspective with energy terms correlated. The Jiles-Atherton model, a nonlinear magnetization model, is employed to quantify the magnetization energy of the Galfenol rod. In order to identify unknown parameters in the Jiles-Atherton model for Galfenol, an optimization program has been developed based on the simulated annealing and the nonlinear least square algorithms. A compact testing structure and a test rig have been developed to characterize and validate the built model. Experimental results show that the time response and the frequency response of the material are accurately predicted by the model. In the frequency range of, the discrepancy between the simulative strain output and the experimental strain output is generally within. The accuracy of the model can also be improved by employing the specific magnetic flux density distribution instead of using the eddy-current loss term. In addition, it is observed that the hysteresis of the response increases with the rising of the excitation frequency. Meanwhile, the dynamic simulation result and the experiment result both agree that the magnitude of the strain output decreases with the increase of the excitation frequency. Not only the work provides a generalized model for longitudinal transducers of Galfenol, but also the energy-based model can be easily modified for complex applications of the Galfenol material.

Acknowledgements

This work was supported by the Natural Science and Engineering Research Council of Canada and the State Key Program of National Natural Science of China (No. 11232009).

Cite this paper

Yimin Tan,Zuguang Zhang,Jean Zu, (2015) Generalized Dynamic Modeling of Iron-Gallium Alloy (Galfenol) for Transducers. Journal of Applied Mathematics and Physics,03,980-988. doi: 10.4236/jamp.2015.38120

References