Journal of Applied Mathematics and Physics
Vol.03 No.08(2015), Article ID:59093,6 pages
10.4236/jamp.2015.38113
Modified Tunneling Radiation of Fermions from a Spherically Symmetric Spacetime with Dark Matter
Zhongwen Feng, Xiaotao Zu
School of Physical Electronics, University of Electronic Science and Technology of China, Chengdu, China
Email: zwfengphy@163.com


Received 7 June 2015; accepted 19 August 2015; published 26 August 2015

ABSTRACT
In the paper, we use the generalized Dirac equation to study the Hawking temperature and entro- py of a spherically symmetric spacetime with the dark matter. The results show that the dark matter can influence the thermodynamic properties of the black hole. Meanwhile, we find the GUP corrected temperature and entropy are not only determined by the nature of black but also re- lated to the properties of tunneling particles. Besides, the GUP can slow down the increase of Hawking temperature and causes the remnants.
Keywords:
Generalized Uncertainty Principle, Spherically Symmetric Spacetime, Dark Matter

1. Introduction
Based on the quantum effect, people found that the black holes can radiate particles [1]. The radiation of black hole got researchers attention, many new methods were presented to study it [2]-[4]. Parikh and Wilzcek put forward the quantum tunneling method, which was an effective method to discuss the black hole’s Hawking radiation. With the help of the quantum tunneling method, they have calculated the massless scalar particle’s tunneling rate and Hawking temperature of the spherically symmetrical spacetime [5]. Then, Kerner and Mann developed the quantum tunneling method and studied the fermions tunneling from Schwarzschild (SC) spacetime [6]. Later, the tunneling behavior of particles with 0 spin, 1/2 spin, 1 spin and 3/2 spin from black holes were investigated via Hamilton-Jacobi ansatz, which is another quantum tunneling method. However, the results obtained in previous work showed that the standard Hawking temperature of black holes was inverse to their mass. As Hawking announced, the black hole would emit all their mass as the temperature increase, this process causes the black holes evaporate over. In other words, black holes would loss all their information, which was called as information paradox of black hole [7] [8].
In order to solve the information paradox problem, people proposed many kinds of correction theories. Recently, people studied the physical properties of the black hole via the generalized uncertainty principle (GUP) [9]-[11]. In quantum gravity theory and string theory, people believe the existence of the minimal observable length, which can be described by the GUP [12] [13] . In [ 14 ], based on the associative Heisenberg algebra
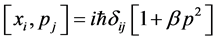 , where
, where 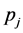 is the momentum operator and
is the momentum operator and 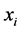 is the position operator. One kind of GUP is expressed as
is the position operator. One kind of GUP is expressed as
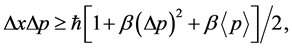 (1)
(1)
with 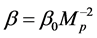 is a small value, which represents the effects of quantum gravity,
is a small value, which represents the effects of quantum gravity, 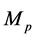 being the Planck
being the Planck
mass [15]. Adopted GUP, Banerjee and Ghosh investigated the thermodynamics of SC spacetime, their results showed that the black hole have remnant mass at the end of evolution [16]. Soon, combining with quantum tunneling method and GPU, the Hawking radiation of Schwarzschild black hole was studied by Nozari and Saghafi [17].
On other hand, astronomers predict 27% of the universe is dark matter. It is natural to think how can the dark matter influence the properties of black hole and whether different corrected methods deduce different results? In this paper, we will apply the GUP to investigate the Hawking temperature and entropy of spherically symmetric black hole with dark matter.
The remainder of the paper goes as follows. In Section 2, we overview of the spherically symmetric black hole with dark matter is provided. In Section 3, we corrected the Hawking temperature and entropy via GUP. The last section is the discussion and concludes.
2. The Spherically Symmetric Spacetime with Dark Matter
In curved space-time, the line element of spherically symmetric black hole with dark matter can be expressed as [18] [19]
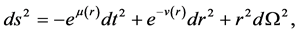 (2)
(2)
where
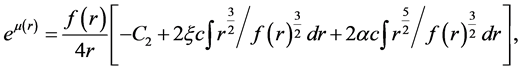 (3)
(3)
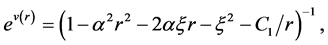 (4)
(4)
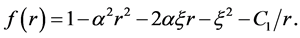 (5)
(5)
In Equation (3)-Equation (5), the ,
,  ,
, 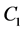 ,
, 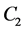 are parameters of the spacetime, note that
are parameters of the spacetime, note that 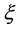 is a parameter of cold dark matter. In order to discuss the tunneling of the black hole, here we let parameter
is a parameter of cold dark matter. In order to discuss the tunneling of the black hole, here we let parameter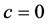 ,
, 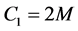 ,
, 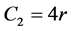
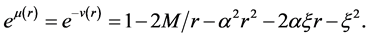
Note that Equation (5) and Equation (6) have the same expression. Thus, one can use 
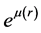
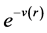
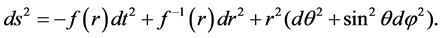
The horizons of this black hole are determined by null super-surface equation. Now, assuming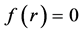
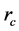
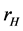
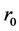
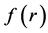
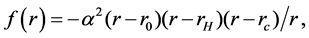
where 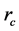
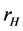
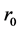
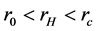
3. The GUP Corrected Hawking Temperature and Entropy of Spherically Symmetric Black Hole with Dark Matter
According to the GUP, Chen et al. have rewritten the original Dirac equation into generalized form. The massless generalized Dirac equation in curved spacetime is [20]
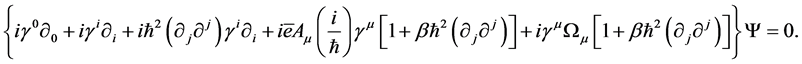
In order to discussing the fermions tunneling from black hole, people assume fermions with 1/2 spin have two states: spin up state and spin down state. Here we only consider the spin up state. The wave function of the spin up state is
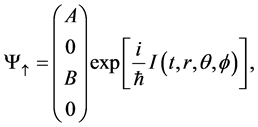
where 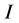
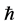
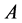
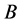
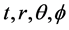
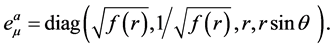
Then, the 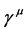
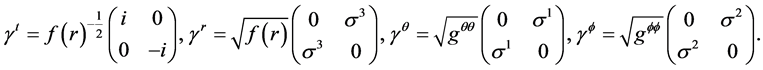
In Equation (12), 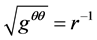
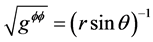
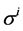
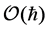
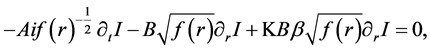
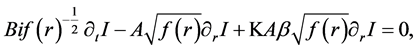
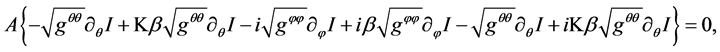
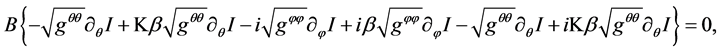
where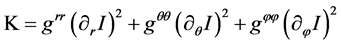
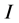
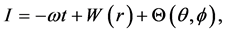
where 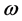
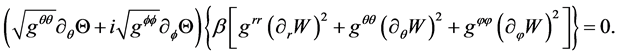
In Equation (18), the 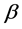
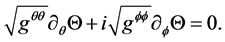
Now, substituting Equation (17) and Equation (19) into Equation (15) and Equation (16), keep the first order term of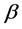
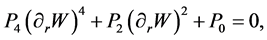
where 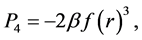
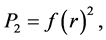

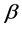
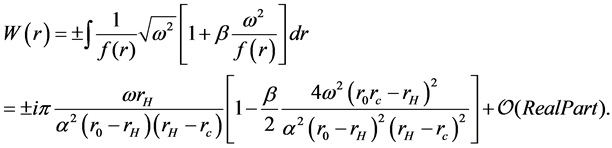
The plus (minus) means the outgoing (ingoing) wave. Here we only keep the imaginary part of Equation (24), because the real part 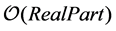
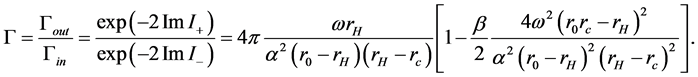
Comparing with the Boltzman factor expression, the GUP corrected Hawking temperature of the black hole with dark matter is
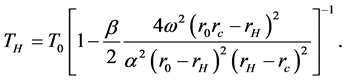
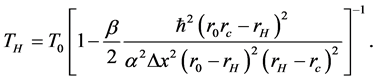
Then, near the event horizon of the black hole, the position uncertainty of a particle can be expressed [21] [22]
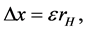
where 
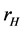
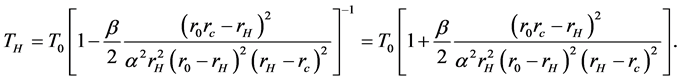
In above equation, we set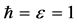
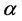
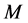
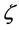
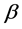
4. Conclusions
In the previous work, people found that the GUP can cause the remnants of black holes. For calculating the remnants, we need neglect the parameters of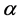
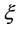
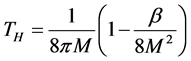
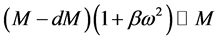
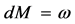
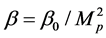
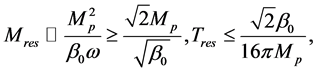
where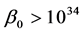
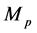
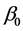
In this work, with the help of GUP, we corrected the thermodynamic properties of spherically symmetric black hole with dark matter. We find that the GUP corrected temperatures is related to the properties of black hole (mass of black hole, 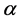
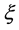
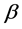
Acknowledgements
This work is supported in part by the Natural Science Foundation of China (Grant No. 11178018).
Cite this paper
Zhongwen Feng,Xiaotao Zu, (2015) Modified Tunneling Radiation of Fermions from a Spherically Symmetric Spacetime with Dark Matter. Journal of Applied Mathematics and Physics,03,931-936. doi: 10.4236/jamp.2015.38113
References
- 1. Hawking, S.W. (1974) Particle Creation by Black Holes. Communications in Mathematical Physics, 43, 199. http://dx.doi.org/10.1007/BF02345020
- 2. Sannan, S. (1988) Heuristic Derivation of the Probability Distributions of Particles Emitted by a Black Hole. General Relativity and Gravitation, 20, 239. http://dx.doi.org/10.1007/BF00759183
- 3. Jiang, Q.Q. (2008) Fermions Tunnelling from GHS and Non-Extremal D1-D5 Black Holes. Physics Letters B, 666, 517. http://dx.doi.org/10.1016/j.physletb.2008.08.005
- 4. Jiang, Q.Q., Han, Y. and Cai, X. (2010) Quantum Corrections and Black Hole Spectroscopy. Journal of High Energy Physics, 49, 49. http://dx.doi.org/10.1007/JHEP08(2010)049
- 5. Parikh, M.K. and Wilczek, F. (2000) Hawking Radiation as Tunneling. Physical Review Letters, 85, 5042. http://dx.doi.org/10.1103/PhysRevLett.85.5042
- 6. Kerner, R. and Mann, R.B. (2008) Fermions Tunnelling from Black Holes. Classical and Quantum Gravity, 25, Article ID: 095014. http://dx.doi.org/10.1088/0264-9381/25/9/095014
- 7. Susskind, L. (2006) The Paradox of Quantum Black Holes. Nature Physics, 2, 665. http://dx.doi.org/10.1038/nphys429
- 8. Susskind, L. (1995) The World as a Hologram. Journal of Mathematical Physics, 36, 6377. http://dx.doi.org/10.1063/1.531249
- 9. Chen, D.Y., Jiang, Q.Q., Wang, P. and Yang, H. (2013) Remnants, Fermions’ Tunnelling and Effects of Quantum Gravity. Journal of High Energy Physics, 11, 176. http://dx.doi.org/10.1007/JHEP11(2013)176
- 10. Chen, D.Y., Wu, H.W. and Yang, H.T. (2013) Fermion’s Tunnelling with Effects of Quantum Gravity. Advances in High Energy Physics, 2013, Article ID: 432412. http://dx.doi.org/10.1155/2013/432412
- 11. Chen, D.Y., Wu, H.W. and Yang, H.T. (2014) Observing Remnants by Fermions’ Tunneling. Journal of Cosmology and Astroparticle Physics, 3, 36. http://dx.doi.org/10.1088/1475-7516/2014/03/036
- 12. Townsend, P.K. (1977) Small-Scale Structure of Spacetime as the Origin of the Gravitational Constant. Physics Review D, 5, 2795. http://dx.doi.org/10.1103/PhysRevD.15.2795
- 13. Garay, L.J. (1995) Quantum Gravity and Minimum Length. Inter-national Journal of Modern Physics A, 10, 145-166. http://dx.doi.org/10.1142/S0217751X95000085
- 14. Kempf, A., Mangano, G. and Mann, R.B. (1995) Hilbert-Space Representation of the Minimal Length Uncertainty Relation. Physics Review D, 52, 1108. http://dx.doi.org/10.1103/PhysRevD.52.1108
- 15. Chen, D.Y., Wu, H.W., Yang, H.T. and Yang, S.Z. (2014) Effects of Quantum Gravity on Black Holes. International Journal of Modern Physics A, 29, Article ID: 1430054. http://dx.doi.org/10.1142/s0217751x14300543
- 16. Banerjee, R. and Ghosh, S. (2010) Generalised Uncertainty Prin-ciple, Remnant Mass and Singularity Problem in Black Hole Thermodynamics. Physics Letters B, 688, 224. http://dx.doi.org/10.1016/j.physletb.2010.04.008
- 17. Nozari, K. and Saghafi, S. (2012) Natural Cutoffs and Quantum Tunneling from Black Hole Horizon. Journal of High Energy Physics, 11, 5. http://dx.doi.org/10.1007/JHEP11(2012)005
- 18. Heydari-Fard, M., Razmi, H. and Sepangi, H.R. (2007) Brane-World Black Hole Solutions via a Confining Potential. Physics Review D, 76, 535. http://dx.doi.org/10.1103/PhysRevD.76.066002
- 19. Shahidi, S. and Sepangi, H.R. (2012) Braneworlds and Dark Matter. International Journal of Modern Physics D, 20, 77. http://dx.doi.org/10.1142/S0218271811018627
- 20. Chen, D.Y. and Li, Z.H. (2014) Remarks on Remnants by Fermions’ Tunnelling from Black Strings. Advances in High Energy Physics, 2014, Article ID: 620157. http://dx.doi.org/10.1155/2014/620157
- 21. Gangopadhyay, S. Minimal Length Effects in Black Hole Thermodynamics from Tunneling Formalism. arXiv:1405.4229.
- 22. Kuchiev, M.Y. and Flambaum, V.V. (2003) Scattering of Scalar Particles by a Black Hole. Physics Review D, 70, 636.
- 23. Majumder, B. (2013) Black Hole Entropy with Minimal Length in Tunneling For-malism. General Relativity and Gravitation, 45, 2403. http://dx.doi.org/10.1007/s10714-013-1581-2

