Journal of Geoscience and Environment Protection
Vol.03 No.06(2015), Article ID:59043,8 pages
10.4236/gep.2015.36015
Seasonal ARIMA Modeling and Forecasting of Rainfall in Warri Town, Nigeria
Daniel Eni, Fola J. Adeyeye
Department of Mathematics/Computer Science, Federal University of Petroleum Resources, Effurun, Nigeria
Email: eni.daniel@fupre.edu.ng, adeyeye.fola@fupre.edu.ng


Received 22 July 2015; accepted 22 August 2015; published 25 August 2015

ABSTRACT
We obtained historical data of rainfall in Warri Town for the period 2003-2012 for the purpose of model identification and those of 2013 for forecast validation of the identified model. Model identification was by visual inspection of both the sample ACF and sample PACF to postulate many possible models and then use the model selection criterion of Residual Sum of Square (RSS), Akaike’s Information Criterion (AIC) complemented by the Schwartz’s Bayesian Criterion (SBC), to choose the best model. The chosen model was the Seasonal ARIMA (1, 1, 1) (0, 1, 1) process which met the criterion of model parsimony with RSS value of 81.098,773, AIC value of 281.312,35 and SBC value of 289.330,84. Model adequacy checks showed that the model was appropriate. We used the model to forecast rainfall for 2013 and the result compared very well with the observed empirical data for 2013.
Keywords:
ACF, PACF, ARIMA, Rainfall, AIC, SBC

1. Introduction
The influence of rainfall on flooding with downstream implication of erosion, water quality, agriculture, sewage system, and tourism among others cannot be over emphasized. For these reasons, early warning of rainfall is very important in the use and management of water resources. [1] noted that the complex nature of atmospheric processes that produced rain made rain modeling and forecasting a very difficult task. [2] [3] remarked that in spite of advances in weather forecasting, accurate rain forecasting was the most challenging task in operational hydrology.
Efforts are being intensified to use time series autoregressive moving average (ARMA) models to forecast hydrological data. The use of ARMA models is justified as a result of its theoretical base in hydrological studies. For example, the parameter value of AR (1) model is the same as the constant due to [4]. Additionally, [5] [6] have used the AR (1) model to predict stream flow generation. [7] used ARMAX model to predict rainfall driven stream flow while [8] used ARX to model storm hydrograph changes under urbanization. In this paper, we take advantage of the seasonal nature of rainfall to use Seasonal ARIMA model to forecast rainfall in Warri town in Delta State, Nigeria.
2. The Area of Study
Warri city is located in latitude 5˚31'N and longitude 5˚45'E with two distinct seasons: the rainy season (May- October) and dry season (November-April). It has mean annual temperature of 32.8˚C and an annual rain amount of 2673.8 mm. Warri is a major oil city located in the Niger Delta region of Nigeria.
The main focus of this work is on determining appropriate Seasonal ARIMA model that can adequately predict rainfall for Warri city.
The seasonal multiplicative ARIMA (Autoregressive, Integrated Moving Average) model is of the form
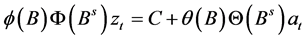 (1)
(1)
where
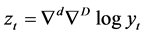
yt is the observed temperature data at time t, 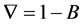 is the regular difference and
is the regular difference and 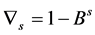 is the seasonal difference. D is the order of the seasonal difference while d is the order of regular difference. C is a constant and
is the seasonal difference. D is the order of the seasonal difference while d is the order of regular difference. C is a constant and 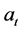 is a white noise process.
is a white noise process.
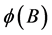 is the regular autoregressive polynomial of order p while
is the regular autoregressive polynomial of order p while 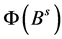 is the seasonal autoregressive polynomial of order P. Similarly,
is the seasonal autoregressive polynomial of order P. Similarly, 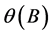 is the regular moving average polynomial of order q while
is the regular moving average polynomial of order q while 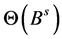 is the seasonal moving average polynomial of order Q. Sometimes, the model (1) is denoted SARIMA (p, d, q) (P, D, Q). The ARIMA model (1) is said to be invertible if all the roots of the moving average polynomial
is the seasonal moving average polynomial of order Q. Sometimes, the model (1) is denoted SARIMA (p, d, q) (P, D, Q). The ARIMA model (1) is said to be invertible if all the roots of the moving average polynomial 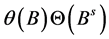 lie outside the unit circle. Note that the model is already stationary. Many models can be formed from (1). These models are made of either past observed values together with a white noise or white noise only or a mixture of both. The major contribution of Box and Jenkins were to provide a general strategy in which three stages of model building were given prominence. These stages are those of model identification, estimation and diagnostic checks (see for example, [9] [10]).
lie outside the unit circle. Note that the model is already stationary. Many models can be formed from (1). These models are made of either past observed values together with a white noise or white noise only or a mixture of both. The major contribution of Box and Jenkins were to provide a general strategy in which three stages of model building were given prominence. These stages are those of model identification, estimation and diagnostic checks (see for example, [9] [10]).
Several researchers and scientist have used these models for several technical and scientific studies. [11] used ARIMA models to model and forecast tourism development in Lithuania while [12] among several others.
3. Material and Method
We obtained historical data of average monthly rainfall for Warri town for the period 2003-2012 for the purpose of model identification and those of 2013 for forecast validation of the chosen model from the National Metrological Center, Oshodi-Nigeria
To detect possible presence of seasonality, trend, time varying variance and other nonlinear phenomena, we inspect the time plot of the observed data side by side with the plots of sample autocorrelation functions (ACF) and sample partial autocorrelation functions (PACF). This will help us determine possible order of differencing and the necessity of logarithmic transform to stabilize variance. Non stationary behavior is indicated by the refusal of both the ACF values, 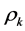 and the PACF,
and the PACF, 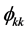 to die out quickly. Also possible seasonal differencing is indicated by large ACF values,
to die out quickly. Also possible seasonal differencing is indicated by large ACF values, 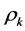 at lags s, 2s … ns. Our technique is to apply both simple and seasonal differencing until data is stationary. Stationary behavior is indicated by either a cut or exponential decay of ACF values
at lags s, 2s … ns. Our technique is to apply both simple and seasonal differencing until data is stationary. Stationary behavior is indicated by either a cut or exponential decay of ACF values 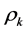 as well as PACF values
as well as PACF values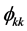 .
.
Model identification is by comparing the theoretical patterns of the ACF and PACF of the various ARIMA models with that of the sample ACF and PACF computed using empirical data. A suitable model is inferred by matching these patterns. Generally [12], ARIMA (0, d, q) is indicated by spikes up to lag q and a cut to zero thereafter of the ACF values 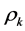 complemented by an exponential decay or damped sine wave of the PACF values
complemented by an exponential decay or damped sine wave of the PACF values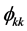 . inversely, ARIMA (p, d, 0) is identified by exponential decay or damped sine wave of the of the ACF values
. inversely, ARIMA (p, d, 0) is identified by exponential decay or damped sine wave of the of the ACF values 

However, the mixed Seasonal ARIMA model is difficult to identify by visual methods of ACF and PACF plots only. In this work, we use the model identification discussed above to give a rough guess of possible values p, q, P, and Q from which several models shall be postulated and then use the model selection criterion of Residual Sum of Square RSS (Box and Jenkins, 1976), Akaike’s Information Criterion AIC [13] to choose the best model. The AIC computation is based on the mathematical formula
The SBC computation is based on the mathematical formula
Having identified a suitable Seasonal ARIMA model, the next stage is the parameters estimation of the identified model and this is done through an exact maximum likelihood estimate due to [15]. While forecast and prediction is by least squares forecast using a least square algorithm due to [16]. When the estimated parameters are not significant, we do correlation analysis to remove redundant parameters.
The test for model adequacy stage requires residual analysis and this is done by inspecting the ACF of the residual obtained by fitting the identified model. If the model is adequate then residuals should be a white noise process. Under the assumption that the residual is a white noise process, the standard error of the autocorrelation
functions should be approximately 
tion functions should fall within the range
process is not white noise.
4. Result and Discussion
To decide on the presence of trend and time varying variances, we inspect the time plot of Warri rainfall data in Figure 1 side by side with the ACF of the data as shown in Figure 2.
Examination of Figure 1 clearly shows presence of time varying variance and seasonal variation while the refusal of the ACF and PACF values to decay in Figure 2 and Figure 3 respectively is an indication of a regular trend. However, we are unable to decide at this stage the presence or otherwise of seasonal trend. We perform a logarithm and first regular difference so as to stabilize the variance and remove the trend. A time plot of rainfall after logarithm and first difference transform is shown in Figure 3 below.

Figure 1. Time plot of rain.
Figure 2. ACF plot of rain.
Figure 3. Time plot of rain (Logarithm transform and first difference).
On inspecting Figure 3, we note the strong presence of seasonal factors. This is confirmed by very high spikes at and around seasonal lags of period 12. The ACF is shown in Figure 4.
We complete the data preparation process by additionally performing a first order seasonal difference and the time plot is shown in Figure 5.
Visual examination of Figure 5 shows that the process is now stationary. For clarity of discussion, we from now on refer to the rainfall data after logarithm, first regular difference and first seasonal difference transformations as the Stationary Process of The rainfall process. Hence we expect a Seasonal ARIMA process of the form
The estimated order of the model parameters p, q, P and Q are identified by visual inspection of ACF and PACF of the stationary process of rainfall shown in Figure 6 and Figure 7.
We expect the ACF in Figure 6 to cut at q + Qs. However, we notice a non-seasonal lag cut at lag1 and a seasonal lag cut at lag24 (note that there is no significant lag at lag36). This suggests a moving average parameter of
Figure 4. ACF plot of rain (Logarithm and first difference).
Figure 5. Time plot of rain (Logarithm, first and seasonal transform).
order one i.e. q = 1 and a seasonal moving average parameter of order two i.e. Q = 2. Similarly from the PACF in Figure 7, we notice a non-seasonal lag cut at lag3 and a seasonal lag cut at lag12 suggesting an AR parameter of order three i.e. p = 3 and a Seasonal autoregressive parameter of order one i.e. P = 1.
Since our strategy is not to have mixed seasonal factors, we postulate two initial models. The two models are: Seasonal ARIMA (3, 1, 1) (1, 1, 0) and Seasonal ARIMA (3, 1, 1) (0, 1, 2). We extend the search to models around these models and based on the model selection criterion of RSES, AIC and SBC, the best model is selected.
The result is shown in Table 1.
From Figure 6, an MA parameter of zero is not possible
From Table 1, we note that in terms of AIC and SBC, the Seasonal ARIMA (1, 1, 1) (0, 1, 1) model performed best. However, it is in competition with Seasonal ARIMA (3 1, 1) (1, 1, 2) that has the lowest RSES. This notwithstanding, we choose Seasonal ARIMA (1, 1, 1) (0, 1, 1) as the best in terms of model parsimony and performance based on AIC and BIC.
We estimated the parameter values of the chosen model as shown below.
Figure 6. ACF plot for stationary rain process.
Figure 7. PACF plot for stationary rain process.
Table 1. Postulated models and performance evaluation.
From Table 2, we note that the MA1 parameter is the only parameter that is not significant. However, we still tolerate it in the model as search for an alternate model did not produce better result.
To verify the suitability of the model, we plot the autocorrelation values of the residual against lag as shown in Figure 8.
We note that on inspection of Figure 8, there is no spike at any lag indicating that the residual process is random. We therefore accepts Seasonal ARIMA (1, 1, 1) (0, 1, 1) as the most appropriate model for forecasting rainfall in Warri town. The model is used to forecast Warri Town Rainfall for the year 2013 and the result is shown in Table 3 below.
A t-distribution test of equality of mean based on Table 3 shows that the difference between the two means is not significant at 5% level of significance. We therefore conclude that the chosen model can adequately be used to forecast rain in Warri Town.
Figure 8. ACF for the residuals.
Table 2. Parameters B in the Model.
Table 3. Forecast for 2014.
5. Conclusion
We have shown that time series ARIMA models can be used to model and forecast the rain in Warri Town. The identified Seasonal ARIMA (1, 1, 1) (0, 1, 1) has proved to be adequate in forecasting rain for at least one year.
Cite this paper
Daniel Eni,Fola J. Adeyeye, (2015) Seasonal ARIMA Modeling and Forecasting of Rainfall in Warri Town, Nigeria. Journal of Geoscience and Environment Protection,03,91-98. doi: 10.4236/gep.2015.36015
References
- 1. French, M.N., Krajewski, W.F. and Cuykendall, R.R. (1992) Rainfall Forecasting in Space and Time Using Neural Network. Journal of Hydrology, 137, 1-31. http://dx.doi.org/10.1016/0022-1694(92)90046-X
- 2. Gwangseob, K. and Ana, P.B. (2001) Quantitative Flood Forecasting Using Multisensor Data and Neural Networks. Journal of Hydrology, 246, 45-62. http://dx.doi.org/10.1016/S0022-1694(01)00353-5
- 3. Hung, N.Q., Babel, M.S., Weesakul, S. and Tri-pathi, N.K. (2008) An Artificial Neural Network Model for Rainfall Forecasting in Bangkok, Thailand. Hydrology and Earth System Sciences, 5, 183-218. http://dx.doi.org/10.5194/hessd-5-183-2008
- 4. James, L.D. and Thompson, W.O. (1970) Least Square Estimation of Constants in a Linear Recession Model. Water Resources Research, 64, 1062-1069. http://dx.doi.org/10.1029/wr006i004p01062
- 5. Fiering, M.B. and Jackson, B.B. (1971) Synthetic Streamflows. Water Resources Monograph No.1, America Geophysical Union, Washington DC.
- 6. Bras, R.L. and Rodri-guez-Iturbe, I. (1993) Random Functions and Hydrology. Dover, New York
- 7. Chang, F.J. and Chen, Y.C. (2001) A Counter Propagation Fuzy-Neural Network Modeling Approach to Real Time Streamflow Prediction. Journal of Hydrology, 245, 153-164. http://dx.doi.org/10.1016/S0022-1694(01)00350-X
- 8. Farahmand, T., Fleming, S.W. and Quilty, E.J. (2007) Detection and Visualization of Storm Hydrograph Changes under Urbanization: An Impulse Response Approach. Journal of Environmental Management, 85, 93-100. http://dx.doi.org/10.1016/j.jenvman.2006.08.004
- 9. McLeod, A. and Lennox, W. (1977) Advances in Box-Jenkins Modeling: Model Construction. Water Resources Research, 13, 577-586. http://dx.doi.org/10.1029/WR013i003p00577
- 10. Mcleod, A.I. (1995) Diagnostic Checking of Periodic Autore-gression Models With Application. The Journal of Time Series Analysis, 15, 221-233. http://dx.doi.org/10.1111/j.1467-9892.1994.tb00186.x
- 11. Brinskiene, M. and Rudzkiene, V. (2005) Modeling and Forecasting of Country Tourism Development in Lithuania. Journal of Environmental Engineering and Landscaping Management, 13, 116-120.
- 12. Brooks, C. (2002) Introductory Econometrics for Finance. Cambridge University Press, UK.
- 13. Akaike, H. (1974) A New Look at the Statistical Model Identification. IEEE Transaction on Automatic Control, 19, 716-723. http://dx.doi.org/10.1109/TAC.1974.1100705
- 14. Schwartz, G.E. (1978) Estimating the Dimension of a Model. Annals of Statistics, 6, 461-464. http://dx.doi.org/10.1214/aos/1176344136
- 15. Melard, G. (1984) A Fast Algorithm for the Exact Likelihood of Autoregressive-Moving Average Models. Applied Statistician, 33, 104-114. http://dx.doi.org/10.2307/2347672
- 16. Brockwell, P.J. and Davis, R.A. (1991) Time Series: Theory and Method. Springer. http://dx.doi.org/10.1007/978-1-4419-0320-4
- 17. Anderson, R.L. (1942) Distribution of Serial Correlation Coefficient. Annals of Mathematical Statistics, 13, 1-13. http://dx.doi.org/10.1214/aoms/1177731638









