 Journal of Software Engineering and Applications, 2011, 4, 411-416 doi:10.4236/jsea.2011.47047 Published Online July 2011 (http://www.SciRP.org/journal/jsea) Copyright © 2011 SciRes. JSEA Propo sing a New Me t ric for Collaborativ e Filtering Arash Bahreh mand 1*, Reza Rafeh2 1Department of Computer Engineering, Islamic Azad University, Arak, Iran; 2Deputy of Computer Engineering, Arak University, Arak, Iran. Email: *stdmwmrule@gmail,com; r-r afeh @ ar aku.ac. ir Received May 21st, 2011; revised June 29th, 2011; accept ed June 30th, 2011. ABSTRACT The aim of a recommender system is filtering the enormous quantity of information to obtain useful information based on the user’s interest. Collaborative filtering is a technique which improves the efficiency of recommendation systems by considering the similarity between users. The similarity is based on the given rating to data by similar users. How- ever, user’s interest may change over time. In this paper we propose an adaptive metric which considers the time in measuring the similarity of users. The experimental results show that our approach is more accurate than the tradition- al collaborative filterin g algorithm. Keywords: Recommendation Systems, Collaborative Filtering, Similarity Metric 1. Introduction In recent years, collaborative filtering has become a widely adopted algorithm in recommendation systems. “Collaborative” means that a group of people with the same interests define their preferences in order to set up the system. CF1 is used to create “recommendation sys- tems” that can, for insta nce, enha nce your experience on a Web site by suggesting music or movies that users might like. This algorithm uses the similarity of other users who have the same history as target user to rec- ommend some items that may be related to his personal interest. The history holds all feedbacks which can be achieved from users by the system. In fact, feedbacks simulate the behavior of users. By analyzing the behavior of users, the similarity values between target user and other members would be recognized and based on these similarities, the items that he has not purchased yet but his similar user s have, will be rec ommended to him. The better you can measure the similarity of users, the better result you a chi e ve i n p re d ict ing the user’s be ha vi or . In the field of social psychology there are many candi- date aspec ts for similarity. But out o f the infinite number of qualities that each person has, some characteristics are more important in determining the similarity of two per- sons. In general, the similarity depends on the system point of view on interactions of users. However, more knowledge about personalities of an individual helps us to make more confident decisions on how similar are humans. In recommendation systems it is also subject to the extent to whic h the syste m is able to capture. M ost of the collaborative filtering algorithms have focused on rating information of users. They believe, ratings deter- mine t he leve l of agre ement or disagr eement o f users for a specific item. But the user interest may change over the time. By increa sing the numbe r of interactions and inte r- connections of people, internet, the probability of transi- tory of interests, personal and social behavior is not far-fetched, therefore; maybe what people want now is likely to variation (is not what they have explored in the past).In general, people have various reactions to events happen in the society. The reflections of these reactions can be observed in e-commerce. Also, the interpretation of each action is related to its time. For instance, suppose a science fiction movie has added to the list of an online movie show site. Users, who are fan of these kinds of movies, would watch and rate it as soon as possible, but those who are not very interested in mentioned type of movie maybe watch it later or when there is no one left in the list which is fascinating from their point of view. Hence we can infer, this group of users is different from pervious users and one of the most important factors which help us to recognize this issue is measuring the 1Collaborative Filtering  412 Proposing a New Metric for Collaborative Filtering Copyright © 2011 SciRes. JS E A level of time distances in interactions of users. An intel- ligent recommender system must be able to adapt itself with current requirements of users. On the other hand, the order of interactions can be a source of semantics which help us in simulating the mentally evolution pro cess of user s. In this research we have presented a new similarity metric which combine different aspect of user behavior in order to better understand who are more similar to each other and who are different from other. Experiment results demonstrate that our contribution improves the accuracy of predictions and evaluate what approach is more effective to satisfy users. The rest of the paper is organized as follows. In Sec- tion 2, we review previous research in the field of colla- borative filtering and analyze most significant metrics which are applied in recommendation system. In Section 3, we propose a novel method to measure the similarity of users by conside ri ng different effective aspects such as time. In Section 4 the experimental results are shown to evaluate the proposed approach. And Section 5 con- cludes the paper. 2. Related Work For a long time recommender systems did not deal with changing user’s interest in their p r e dictions. For example, similarity of users was constant in different time periods and training datasets were considered as a static resource. In memory-based collaborative filtering, predictions are based on preferences of neighbor users or items. A widespread approach in memory-based collaborative filtering is the k-nearest neighbor algorithm. In [1] two imputed neighborhood based collaborative filtering algo- rithms are proposed that improved the performance of recommender system in very sparse rating data. Another popular technique is the top-N recommendations which recommends a set of N top-sorted items which probably will be interesting items by a target user [2,3]. However hybrid approaches are recognized as a way to alleviate the scaling and sparsity problem without any optimized solution when the content of environment changes dy- namically over the time. In [4] the history period is divided into intervals with different length the similarity is computed in each inter- val separately. But the way of determining initial time interval and length of each time inter val, consideri ng the conditions of each system is not described. A critical step in K-nearest algorithm is the neighbor- hood formation which means finding a special subset of the co mmuni ty for target user by recognizing others with analogous behavior to act as recommenders. In order to, every pair of users profile to be computed, to measure the degree of similarity, , shared between all pairs a and b [5]. The core objective of similarity metrics is evaluating potential relationship between users with a numeric value. Jaccard similarity has focused on the amount of over- lap between users based on the amount of shared items in each pair. However, the value of the user’s rate is neg- lected [6]. Equation (1) describes this metric in more details in which dete rmine s the rat ing o f user u for item i. ,, , ,, ui vi uv ui vi RR Sim RR ∩ =∪ (1) One o f the most widespread methods in measuring the similarity of t wo users is Pea rson Correlation Coe fficient (PCC) which aims to analyzing the behavior of user, considering ratings input by each user [7]. As you see in Equation (2) ratings are normalized by subtracting the user’s mean rating, , because each user may have a particular rating scale. I is the set of common items be- twee n user u and v. De spite the pop ularity of PCC, it has been the subject to a number of modifications that will be discussed later in a more exact wa y . ( )() () ( ) ,, ,22 ,, ui uvi v iI uv ui uvi v iI iI RRR R Sim RR RR ∈ ∈∈ −− = −− ∑ ∑∑ (2) Another si milarity metric s is co sine similarit y as in (3) that two users are compared as two vectors, while the similarity between them depends on their cosine angle [8]. The main application of cosine similarity is evaluat- ing the similarity of two documents by tracing each document as a vector of word frequencies and computing the cosine of the angle formed by the frequency vectors [9].In collaborative filtering, users or items which are corresponding to documents and ratings are used instead of word frequencies. ,, ,22 ,, ui vi iI uv ui vi iI iI RR Sim RR ∈ ∈∈ =∑ ∑∑ (3) Shanle Ma [10] presented a hybrid recommender sys- tem to cope with the interest d rifting proble m that used a time-sensitive-f unction. One of the most related works to our study is [5] that investigated on the performance of collaborative filtering over time in which the similarity of user s change s with ti me. But it was almo st an anal yti- cal research but a clear way to cope relevant problem was not presented. In all mentioned approaches, there is no difference in similarity of users considering items rated either in the same timestamps or dissimilar timestamps. In other  Proposing a New Metric for Collaborative Filtering Copyright © 2011 SciRes. JSEA words, the behavior of users is not monitored w.r.t time. There is still an open issue of measuring similarity in which comparing prediction accuracy demonstrates that one similarity measure can outperform another one based on the particular dataset. 3. Proposed Metric There is a public standard notation to describe CF prob- lems. The input can be structured as an M × N interact ion matrix, A, associated with M user and N items . In this matrix, can take the value of either 0 or 1, which 1 represents an ob- serving transaction between and (for example, has purchased .) and 0 represents the absence of any transaction. By using this matrix the level of user’s in- terest for different items can be shown. For analyzing the behavior of users in a more exact way we need to know the time that each interaction is occurred. As we men- tioned earlier, one important factor on the performance of similarity metrics is the ability of the recommender sys- tem to record the different type of feedback from users. There are several types of feedbacks which can be cap- tured in these syste ms such as rating, listening habits for music recommendation and comments in e-commerce web site. We analyze relation of two users in four phases and then combine these factors to compute the final result as the similarity amon g the m. Actua lly, the main p urpo se o f this step is calculating the difference between user’s in- terests. Four factors are important for the final weight: a) The number of common ite ms . b) The degree of user’s interest in common items. c) Timestamp of rated ite ms. d) Rating s equences. However it is unclear which factor plays more impor- tant role. Considering conditions and goals of our busi- ness, each factor may have various effects on the final weight between users. For example, if there is no appro- priate rating definitio n to eval uate the user ’s interes t for a specific item, the first factor plays more important ro le . If the s yste m and use rs ha ve a d ynamic b ehav ior in vario us time intervals, the third factor becomes more important. In the following, we explain how each factor is con- tributed in the proposed metric. 3.1. The Number of Common Items The number of common items between users u and v, , is first fac tor which is consid ere d in our calc ula- tion. To normalize the value we use . This function returns the number of all possible common items [11]. If one rates 10 items and the other one rates 5 items, they can have up to 5 common items. Therefore, Proportion in (4) is a normal value (range from 0 to 1) which repr e sents the first similarity factor. , , Proportion uv uv NCI MaxCI = (4) 3.2. The Degree of User’s Interest in Common Items The Equation (5) is the sum of rate differences between two users (u and v) and CI indicates the set of items which are in common between them. , ,,uvui vi i CI SORDR R ∈ = − ∑ (5) To measure rating difference factor, Equation (6) is applied as which determines the max- imum difference that may occur between u and v w.r.t. item’s rate. For example, if numerical feedback of the system is 5-star, we have: ,, 4* uv uv MaxRateDiff NCI= (6) In order to measure the similarity of a pair by consi- dering the first two factors, we use the following equa- tion: , 1/ , , Proportion*1 uv EOR uv uv BaseWeight SORD MaxRateDiff = − (7) EOR implies the effect of item’s rate factor and is greater than one. By increasing the value of EOR, the difference between users becomes more important. 3.3. Timestamps of Rated Items The users’ similarity increases when they have more common time distance. The Equation (8) implies sum of time distance among u and v and is the time of rat- ing i by u s er u. , ,,uvui vi i CI SOTDT T ∈ = − ∑ (8) Consequently for the time factor we use (9) as an adaptive decay function. In this equation α is exploited for the purpose of adaptability which depends on the system’s time s cale (α > 0). ( ) , , , uv uv uv DF SOTDSOTD NCI α α = + (9) Thr ough a lear ning pr ocess we can tune α to make the method more accurate. We will discuss this subject in Section 4. 3.4. The Sequence of Rated Items In this section the distance between users w.r.t. interac-  414 Proposing a New Metric for Collaborative Filtering Copyright © 2011 SciRes. JS E A tions order is computed. If items rated by the user are kept in a queue, each item has a priority number. There- fore the distance can be calculated according to the fol- lowing equation. , ,,uvui vi i CI SOPDP P ∈ = − ∑ (10) In above equation, is the priority of item i in u’s item queue. For example in Figure 1, =4 In order to determine the distance order (interaction sequence) of u1from u2 and u3 in Figure 1, (10) is applied. As Figure 1 shows, 7 items are in common among all users. The common items queue is illustrated as a link list. Accord- ing to (10), we have =24 and =6, therefore u3is more similar to u1 in comparison with u2 w.r.t. interactions order. A normal value for calculating the impact of time in final result is needed. In (11), is a no rmal value (rang from 0 a nd 1) that uses functi on i n (1 2) which i mplie s the ma ximu m dissimilarity of interactions sequence of a user to another one when they have n common items. , , () uv uv SOPD NSOPD MSOPD n = (11) ( ) 2 2 2 2if is odd 2 () 2 otherwise n nn n MSOPD n n −− = (12) Using linear combination which is shown in (13), the distance between two users can be computed in w.r.t. rated items timestamp and order of common items. ( ) ( ) ( ) ,, , 1 1 uv uvuv TFDF SOTDNSOPD αβ αβ = +− += (13) Finally, the similarity between two users by consider- ing all four factors can be measured through (14) in whic h EOT deter mines ho w the val ue of can effect on the final res ult. Figure 1. u1, u2 and u3 have purchased same items (A G) in differ ent orders. ( ) ( ) ( ) ,, , * 1* uv uvuv SimBaseWeightEOTEOT TF= +− (14) In above equation, 0 < EOT < 1 and 4. Evaluation To evaluate the performance of our proposed metric, we need to apply it in creating recommendation process and compare the result with classic collaborative filtering algorithm2. Therefore the Weighted Sum of Other Rat- ings [7] is used to generate recommendations. The value of is calculated based on our metrics in the pre- vious step. In this formula U is the collection of k-most similar user to u. ( ) ,, ,, . v vi uv vU u ui uv RR Sim RR Sim ∈ − = + ∑ (15) Statistical Accuracy Metrics evaluate the accuracy of a system by comparing the numerical recommendation rate on training dataset against the real user provided value for the user-item pairs in the test dataset [12,13]. In this study Mean Absolute Error (MAE) is used as one of the widely adopted metric for evaluation. Where n is the total number of ratings over all users, is the pre- dicted rating for user i on item j, and is the actual rating. A lower MAE means a b e tte r prediction [14]. (16) We have chosen MovieLens dataset as one of the most prevalent and reliable datasets for evaluation and com- parison of recommender systems. MovieLens was col- lected through the MovieLens project, and was distri- buted by GroupLens Research Group at the University of Minnesota. However, each vote is accompanied by a time stamp, but for our own purpose, it is not an appro- priate source for evaluating our research. For example, most of the time stamps belong to the time that the sys- tem as ke d the o p inion o f t he u se r, no t to the first ti me the user has seen the movie. Therefore, a user may rate 100 items in one da y. As it can be seen in Figure 2 t he resul t of analyzing Movielens dataset shows that 55% of users inter acted with the system in onl y one d ay. As we mentioned before our approach can adopt itself to different circumstances and limitations of the target system. Because of this adaptively, the algorithm should be customized to our qualifications and concepts of our business. For achieving this purpose some parameters such as EOR, EOT and α should be set up. Figure 3 shows the effect of each parameter with 200 neighbors 2 In classic approach, PCC is applied as the similarity metric and Wei g hted Sum of O ther’s Ra ting s a s the re co m mendatio n m ethod . 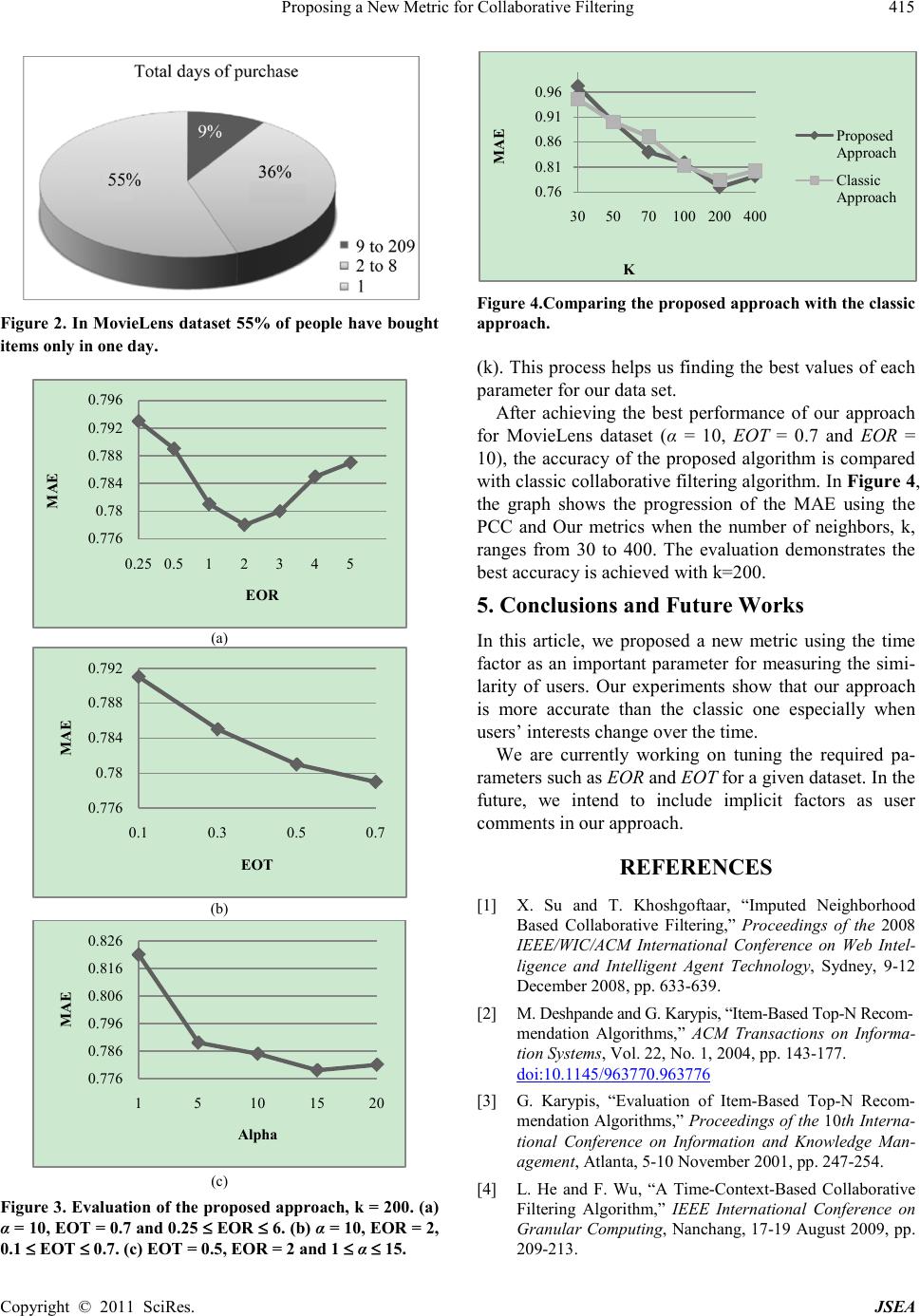 Proposing a New Metric for Collaborative Filtering Copyright © 2011 SciRes. JSEA Figure 2. In MovieLens dat aset 55 % of people have bought items only in one day. (a) (b) (c) Figure 3. Evaluat ion of the pr opose d app roach, k = 200. (a) α = 10, EOT = 0.7 and 0.25 ≤ EOR ≤ 6. (b) α = 10 , EO R = 2, 0.1 ≤ EOT ≤ 0.7. (c) EOT = 0.5, E O R = 2 and 1 ≤ α ≤ 15. Figure 4. Compar ing the pr op osed a ppr oac h wi th the class ic appr o ach. (k). This process helps us finding the best values of each parameter for our data set. After achieving the best performance of our approach for MovieLens dataset (α = 10, EOT = 0 .7 and EOR = 10), the accuracy of the proposed algorithm is compared with classic colla borative filte ring algor ithm. In Figure 4, the graph shows the progression of the MAE using the PCC and Our metrics when the number of neighbors, k, ranges from 30 to 400. The evaluation demonstrates the best accuracy is achieved with k=200. 5. Conclusions and Future Works In this article, we proposed a new metric using the time factor as an important parameter for measuring the simi- larity of users. Our experiments show that our approach is more accurate than the classic one especially when users’ interests change over the time. We are currently working on tuning the required pa- rameters such as EOR and EOT for a given dataset. In t h e future, we intend to include implicit factors as user comments in our approach. REFERENCES [1] X. Su and T. Khoshgoftaar, “Imputed Neighborhood Based Collaborative Filtering,” Proceedings of the 2008 IEEE/WIC/ACM International Conference on Web Intel- ligence and Intelligent Agent Technology, Sydney, 9-12 December 2008, pp. 633-639. [2] M. Des h pan de an d G. Ka r ypis, “Item-Based Top-N Recom- mendation Algorithms,” ACM Transactions on Informa- tion Systems, Vol. 22, No. 1, 2004, pp. 143-177. doi:10.1145/963770.963776 [3] G. Karypis, “Evaluation of Item-Based Top-N Recom- mendation Algorithms,” Proceedings of the 10th Intern a- tional Conference on Information and Knowledge Man- agement, Atlanta, 5-10 November 2001, pp. 247-254. [4] L. He and F. Wu, “A Time-Context-Based Collaborative Filtering Algorithm,” IEEE International Conference on Granular Computing, Nanchang, 17-19 August 2009, pp. 209-213. 0.776 0.78 0.784 0.788 0.792 0.796 MAE EOR 0.776 0.78 0.784 0.788 0.792 MAE EOT 0.776 0.786 0.796 0.806 0.816 0.826 MAE Alpha 0.76 0.81 0.86 0.91 0.96 MAE K Proposed Approach Approach  416 Proposing a New Metric for Collaborative Filtering Copyright © 2011 SciRes. JS E A [5] N. Lath ia, “Evaluating Collaborative Filtering over Time,” Ph.D. Thesis, University College London, London, 2010. [6] M. Charikar, “Similarity Estimation Techniques from Rounding Algorithms,” Annual ACM Symposium on The- ory of Computing, Montreal, 19-21 May 2002, pp. 380- 388. [7] P. Resnick, N. Iacovou, M. Suchak, P. Bergstrom and J. Riedl, “Grouplens: An Open Architecture for Collabora- tive Filtering of Netnews,” ACM Conference on Comput- er Supported Cooperative Work, New York, 22-26 Octo- ber 1994, pp. 175-186. [8] B. M. Sarwar, G. Karypis, J. A. Konstan and J. Riedl, “Analysis of Recommendation Algorithms for E-Com- merce,” ACM Conf erence on Electron ic Commerce, New York, 17-20 October 2000, pp. 158-167. [9] G. Salton and M. McGill, “Introduction to Modern In- formatio n Retrieval,” Facet Pub lishing, New York, 1983. [10] S. Ma, X. Li, Y. Ding and M. E. Orlowska, “A Recom- mender System with Interest-Drifting,” 8th International Conference on Web Information Systems Engineering, Nancy, 3-7 December 2007, pp. 6 33-642. [11] T. Segaran, “Programming Collective Intelligence,” O'R- eilly Media, Sebastopol, 2007. [12] K. Goldberg, T. Roeder, D. Gupta and C. Perkins, “Ei- gentaste: A Constant Time Collaborative Filtering Algo- rithm,” Information Retrieval, Vol. 4, No. 2, 2001, pp. 133-151. doi:10.1023/A:1011419012209 [13] J. L. Herlocker and J. A. Konstan, “Evaluating Collabora- tive Filtering Recommender Systems,” ACM Transac- tions on Information Systems, Vol. 22, No. 1, 2004, pp. 5-53. doi:10.1145/963770.963772 [14] X. Su and T. Khoshgoftaar, “A Survey of Collaborative Filtering Techniques,” Advances in Artifici al Intelli gence, Vol. 2009, 2009, pp. 1-20. doi:10.1155/2009/421425
|