 America n Journal of Analy tic al Chemistry, 2011, 2, 324-331 doi:10.4236/ajac.2011.23040 Published Online July 2011 (http://www.scirp.org/journal/ajac) Copyright © 2011 SciRes. AJAC A Study of the Behavior of Alkyl Side Chains Phenols and Arenes in Polar and Nonpolar GC Stationary Phases Pavel Straka1*, Petr Bury an 2 1Institute of Rock Structure and Mechanics, Academy of Sciences of the Czech Republic, Prague, Czech Republic 2Institute of Chemical Technology, Prague, Czech Republic E-mail: straka@irsm.cas.cz Received July 17, 2010; revised January 10, 2010; accepted J anuar y 20, 2011 Abstract Gas chromatographic measurements of the relative retention times of alkyl-substituted arenes and phenols on capillary columns at temperatures of 125˚C - 140˚C have shown that logarithms of retention times increase bi-linearly with the number of carbon atoms in the molecule. It was found that in a high density stationary phase, the longer alkyl side chains of compounds in question are subject to cyclization as a result of the re- sistance force of this phase affecting molecules during their thermal and diffusion motion. Consequently, common conventional aromatic-aliphatic molecules become new molecules with quasi-alicyclic rings. In comparison with the conventionally conceived molecules, the resulting aromatic-quasi-alicyclic molecules are characterized by rather different, possibly even completely different non-covalent interactions between the molecules, which then affect the retention characteristics. Moreover, cyclization facilitates the mixing of n-alkyl arenes or n-alkyl phenols with high-molecular stationary phases, because the thermodynamic condi- tion for mixing is better fulfilled. Keywords: Alkyl Phenols, Alkyl Benzenes, Reten ti on Times, Mol ecu lar Mec hanics, Van der Waa ls Forces 1. Introduction The following considerations presented were based on gas c hromato gr aphic measurements on capillary columns (50 m, an internal diameter of 0.25 mm) with stationary phases Apiezon K (nonpolar) and tri (2,4-xylenyl) phos- phate-phosphoric acid (95:5) (polar) [1-6]. The mea- surements of the relative retention times ( ) of n-alkyl phenols and n-alkyl benzenes C7-C12 on these capillary columns with both polar and nonpolar station- ary phases at temperatures of 125°C - 140°C showed that the logarithms of these retention times increase bi-linearly with the number of carbon atoms in a mole- cule ( ) (Figure 1) [1]. Two linear areas in the consecu- tive intervals C7-C9 and C9-C12, with the slopes of each line being different, were proven in the re lation (where and are constants), al- though only one line had been anticipated to be found. The complete dependence was thus of a bi-linear charac- ter. This dependence was also found under the mentioned conditions in the case of n-alkyl phenol methylethers [1]. In classic considerations on the dependence of reten- tion t imes on the number o f carbo ns in differe nt ho- mo- logous series of gas chromatographically separated sub- stances, purely linear dependence without any diver- gence is always considered, be it for isotherm or non- isotherm separatio ns [2-6]. Howe ve r, the divergence detected in the dependence suggests that the behavior of mole- cules o f the c ompound s in q uestio n duri ng sepa rations in stationary phases is more complicated than has been as- sumed by the classic considerations. The relation should be expected to be purely linear as a r esult o f the gr owing number of ca rbon a toms i n the molecule [2-6] and the corresponding increase of or more precisely with boiling points (b ) of the given homologs ( ). The men- tioned purely linear relation has frequently been applied in the identification of unknown substances using data acquired through gas chromatographic separations, but the valid i ty of t his u s age is questionable. In the study [1], the relative retention times were ex- pressed as a logarithm of the ratio of the retention ti me of the given n-alkyl phenol substituted in the ortho, meta and para positions and pheno l, and in the case of n-alkyl benzenes as a logarithm of the ratio of the retention time 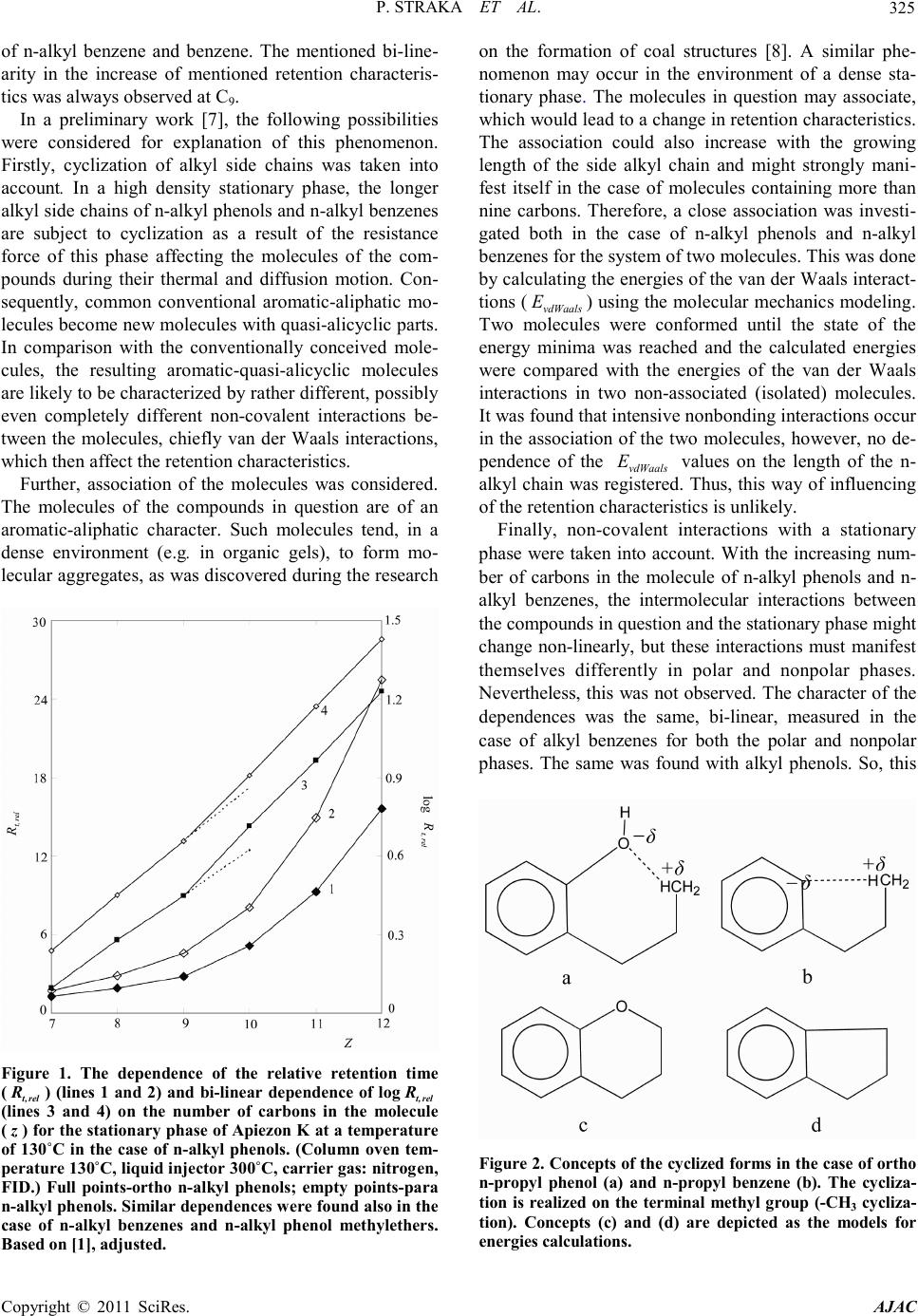 P. STRAK A ET AL. Copyright © 2011 SciRes. AJAC 325 of n-alkyl benzene and benzene. The mentioned bi-line- arity in the increase of mentioned retention characteris- tics was always observed at C9. In a preliminary work [7], the following possibilities were considered for explanation of this phenomenon. Firstly, cyclization of alkyl side chains was taken into account. In a high density stationary phase, the longer alkyl side chains of n-alkyl phenols and n-alkyl benzenes are subject to cyclization as a result of the resistance force of this phase affecting the molecules of the com- pounds during their thermal and diffusion motion. Con- sequently, common conventional aromatic-aliphatic mo- lecules become new molecules with quasi-alicyclic pa rts. In comparison with the conventionally conceived mole- cules, the resulting aromatic-quasi-alicyclic molecules are likely to be characterized by rat her d i fferent, possibly even completely different non-covalent interactions be- tween the molecules, chiefly van der Waals interactions, which then affect the retention characteristics. Further, association of the molecules was considered. The molecules of the compounds in question are of an aromatic-aliphatic character. Such molecules tend, in a dense environment (e.g. in organic gels), to form mo- lecular aggregates, as was discovered during the research Figure 1. The dependence of the relative retention time ( ) (lines 1 and 2) and bi-linear dependence of log (lines 3 and 4) on the number of carbons in the molecule ( ) for the s tation ary phase of Apiez on K at a temperature of 130˚C in the case of n-alkyl phenols. (Column oven tem- perature 1 30˚C, liquid injector 300˚C, carrier gas: nitrogen, FID.) Full points-ortho n-alkyl phenols; empty points-para n-alkyl ph en ol s. S i mil ar de pe nd enc e s wer e f ound al so i n th e case of n-alkyl benzenes and n-alkyl phenol methylethers. Based on [ 1], adjus ted. on the formation of coal structures [8]. A similar phe- nomenon may occur in the environment of a dense sta- tionary phase. The molecules in question may associate, whic h woul d l ea d to a c hange in retention characteristics. The association could also increase with the growing length of the side alkyl chain and might strongly mani- fest itself in the case of molecules containing more than nine carbons. Therefore, a close association was investi- gated both in the case of n-alkyl phenols and n-alkyl benz enes for the system of two mole cule s . T hi s was done by ca lcula tin g the ene rgie s o f the van der Waals interact- tions ( ) usin g the molecular mechanics modeling. Two molecules were conformed until the state of the energy minima was reached and the calculated energies were compared with the energies of the van der Waals interactions in two non-associated (isolated) molecules. It was fo und that intensive nonbonding interactions occur in the association of the two molecules, however, no de- pendence of the values on the length of the n- alkyl chain was registered. Thus, th is way of influencing of the rete ntion charac te ristics is u nlikely. Finally, non-covalent interactions with a stationary phase were taken into account. With the increasing num- ber of carbons in the molecule of n-alk yl phenols and n- alkyl benzenes, the intermolecular interactions between the compounds in question and the stationary phase might change non-linearly, but these interactions must manifest themselves differently in polar and nonpolar phases. Nevertheless, this was not observed. The character of the dependences wa s the same, bi-linear, measured in the case of alkyl benzenes for both the polar and nonpolar phases. The same was found with alkyl phenols. So, this Figure 2. Concepts of the cyclized forms in the case of ortho n-propyl phenol (a) and n-propyl benzene (b). The cycliza- tion is realized on the terminal methyl group (-CH3 cycli z a- tion). Concepts (c) and (d) are depicted as the models for energies calculations.  P. STRAK A ET AL. Copyright © 2011 SciRes. AJAC 326 interpretation of the observed retention phenomena wa s abandoned. Therefore, it wa s the cyclization alkyl chains of the considered compounds that was preferred. The preference for the cyclizatio n ari ses also from the fact that alicyclic-aromatic ethers with five- and six-membered alicyclic rings with oxygen and an interconnected aro- matic ring (Figure 2), which are thermodynamically sta- ble compounds, are formed. The mentioned phenomena can be evaluated and com- pared using method s of comput at ional che mistr y. In order to assess cyclization, association and different interac- tions, the energies of the co valent bond s and non-covalent interactions, mainly van der Waals, can be computed. For the purpose of this assessment, molecular conformations which are realistic and energetically advantageous or pos- sible and are in correlation with the ascertained chroma- tographic data can also be estimated. On the basis of ex- perience with the evaluation of aromatic, aromatic-ali- phatic, aromatic-alicyclic and phenolic structures in terms of energy using the methods of molecular mechanics [7- 9], two methods of molecular mechanics were selected for the calculations (see below). Recently, the molecular mechanics method was successfully used to study cycli- zation reactions [10]. The aim of the presented work is to explain the bi- li- nearity in the logarithmic dependence of the relative re- tention time on the number of carbons in the molecule in the case of n-alkyl phenols and n-alkyl benzenes by mo- lecular mechanics modeling and to clarify the beha vior of these compo und s in the environment o f a stationar y phase of a ca pilla ry co lumn. T he potential energies of the bonds and interactions have been considered for the cal- cula- tions. 2. Calculations In our considerations, the retention data obtained on a nonpolar stationary phase of Apiezon K and a polar sta- tionar y phase of trixylenylpho spha te-phosphoric acid (95: 5) at a temperature of 130˚C according to [1] were taken into account . For the calculations, the molecular mechanics methods were selected [11-13] and two force fields, MM+ and AMBER, were used. The reason is that these methods use analytical and relatively simple potential energy functions for describing the interactions between a set of atoms; further, they are empirical and accurate and very suitable for small organic molecules. What is important is that the atom types, not atoms, are the fundamental basis for cal- culat ing the interactions. In these methods, the interaction potential describes both bonding and non-bonding inter- actions. In the potential, the following energetic terms were calculated: - bond stretching ( ), which is associated with the deformation of a bond from its standard equilib- rium length; - bond angle bendi ng ( ), which is associated with the deformation of an angle from its normal value; - stretch-bend ( )—the bond-stretching and angle-bending cross term, which includes coupling between the bond stretching and angle bending; - dihedral s ( )—the torsional energy, which is associated with the tendency of dihedral angles to have a cer tain n-fold symmetry and to have minimum ener gy; - van der Waals ( ), which describes the repulsive forces keeping two non-bonded atoms apart at close range and attrac tive forces drawing them toge ther at long range; - electrostatic (elst E), which describes the non- bonded electrostatic interactions, particularly dipole-di- pole interactions. These energetic terms were calculated both by the MM+ and AMBER methods, with the exception of , which was calculated only by means of the MM+ method. The mentioned potential energies of the covalent bonds and non-covalent interactions were calculated for com- mon (co nventional) n-alkyl phenols and n-alkyl benzenes and also for the models of the cyclized forms of these compounds. The concepts of the cyclized forms were formulated on the basis of the study of the distribution of electron densities (atomic charges in a molecule) in common and cyclized molecules. As expected, in n-alkyl phenol molecules, a high electron density was found on the oxygen of the hydroxyl gro up and a very low elec tron density on hydrogens of the terminal methyl group. The closing of the alicyclic ring was thus easily implemented by the hydrogen bridge as shown in Figure 2(a). The concept of the cyclized form of alkyl benzenes was more complicated. The electron density on the methyl carbon was disc o vered to b e c o nsiderab l y higher tha n o n the ot h- er c arbons and, e specially, o n hydrogen atoms of the me- thyl group in an alkyl chain. The closing of the ali- cyclic ring was thus implemented by an interaction of methyl hydrogen with the ascribed charge and the benzene ring with the ascribed charge (Figure 2(b)). The basic concepts of cyclized forms and models of these forms, for the sake of calculations demonstrated on n- propyl phenol and n-propyl benzene, are shown in Fig- ures 2(c) and 2(d), namely for the case of alicyclic ortho n-propyl phenol and alicyclic n-propyl benzene. In the latter case, n-propylbenzene is cyclized to the ortho posi- tion with respect to the propyl. The cyclization here is implemented on the terminal methyl group (-CH3 cycliza- tion). Besides the -CH3 case, cyclization was also considered 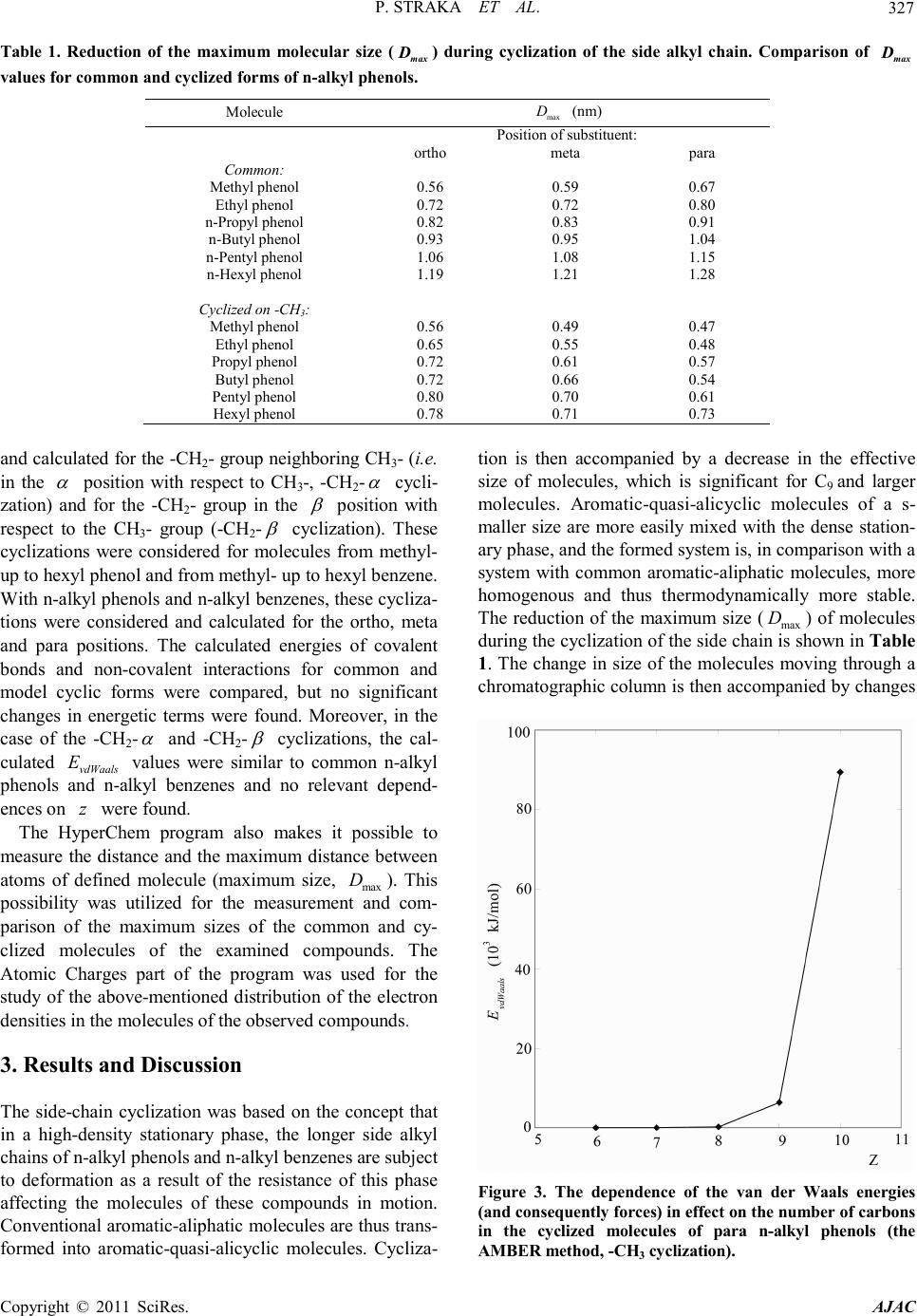 P. STRAK A ET AL. Copyright © 2011 SciRes. AJAC 327 Table 1. Reduction of the maximum molecular size ( ) during cyclization of the side alkyl chain. Comparison of values for common and cyclized for ms of n-al kyl phe nol s. Molecule (nm) Posit ion of subs tituent: Ethyl phenol 0.65 0.55 0.48 and calcul ated for the -CH2- gro up neighboring CH3- (i.e. in the position with respect to CH3-, -CH2- cycli- zation) and for the -CH2- group in the position with respect to the CH3- group (-CH2- cyclization). These cyclizations were considered for molecules from methyl- up to hexyl phenol and from methyl- up to hexyl benzene. With n-alkyl phenol s and n-alkyl benzenes, these cycliza- tions were considered and calculated for the ortho, meta and para positions. The calculated energies of covalent bonds and non-covalent interactions for common and model cyclic forms were compared, but no significant changes in energetic terms were found. Moreover, in the case of the -CH2- and -CH2- cyclizations, the cal- culated vdWaals E values were similar to common n-alkyl phenols and n-alkyl benzenes and no relevant depend- ences on were found. The HyperChem program also makes it possible to measure the distance and the maximum distance between atoms of defined molecule (maximum size, ). This possibility was utilized for the measurement and com- parison of the maximum sizes of the common and cy- clized molecules of the examined compounds. The Atomic Charges part of the program was used for the study of the above-mentioned distribution of the electron dens itie s in t h e mole c u l es of the o bs erved compou nds. 3. Results and Discussion The side-chain cyclization was based on the concept that in a high-density stationary phase, the longer side alkyl chains of n-alkyl phenols and n-alkyl benzenes are subject to deformation as a result of the resistance of this phase affecting the molecules of these compounds in motion. Convent ional a romatic-al ipha tic mo lecules ar e thus tra ns- formed into aromatic-quasi-alicyclic molecules. Cycliza- tion is then accompanied by a decrease in the effective size of molecules, which is significant for C9 and larger molecules. Aromatic-quasi-alicyclic molecules of a s- maller size are more easily mixed with the dense station- ary pha se, and the formed system is, in compari son with a system with common aromatic-aliphatic molecules, more homogenous and thus thermodynamically more stable. The reduction of the maximum size ( ) of molecules duri ng the cyclizatio n of the side chai n is shown in Table 1. The change in size of the molecules moving through a chromato graphic column is the n accompanied by c hange s Figure 3. The dependence of the van der Waals energies (and conse quently forc es) in effect on the number of carbons in the cyclized molecules of para n-alkyl phenols (the AMBER method, -CH3 cyclization). 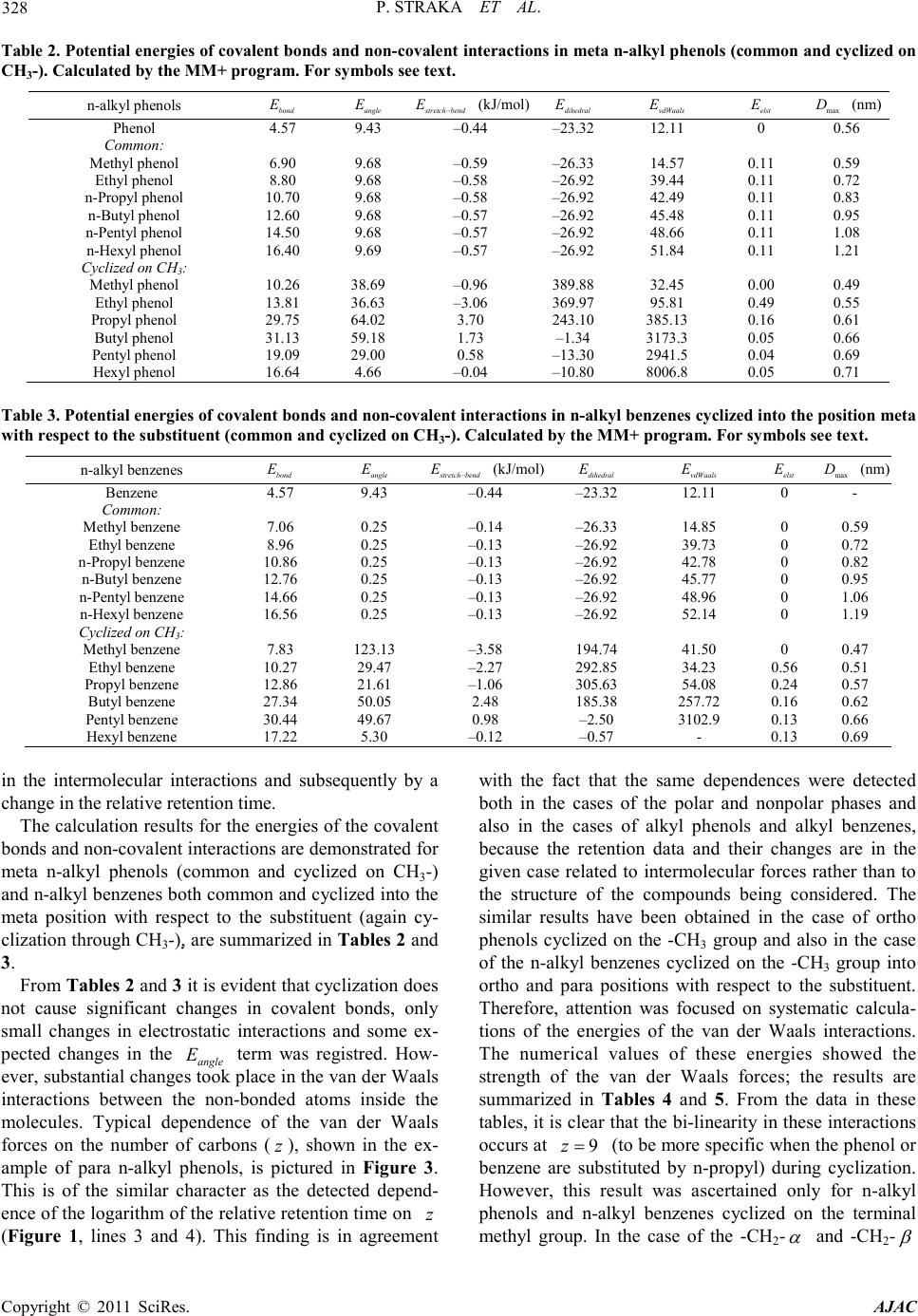 P. STRAK A ET AL. Copyright © 2011 SciRes. AJAC 328 Table 2 . Pote ntial en ergi es of cov alent b ond s and non-co vale nt i nteracti ons i n meta n-alkyl phenols (common and c ycl ize d on CH3-). Calc ulated by the MM+ program. For symbols see text. n-alkyl phenols (kJ/ mol) (nm) Methyl phenol Ethyl phenol n-Propyl phenol n-Butyl phenol n-Pentyl phenol 6.90 8.80 10.70 12.60 14.50 9.68 9.68 9.68 9.68 9.68 –0.59 –0.58 –0.58 –0.57 –0.57 –26.33 –26.92 –26.92 –26.92 –26.92 14.57 39.44 42.49 45.48 48.66 0.11 0.11 0.11 0.11 0.11 0.59 0.72 0.83 0.95 1.08 3 Methyl phenol Ethyl phenol Propyl phenol Butyl phenol Pentyl phenol 10.26 13.81 29.75 31.13 19.09 38.69 36.63 64.02 59.18 29.00 –0.96 –3.06 3.70 1.73 0.58 389.88 369.97 243.10 –1.34 –13.30 32.45 95.81 385.13 3173.3 2941.5 0.00 0.49 0.16 0.05 0.04 0.49 0.55 0.61 0.66 0.69 Table 3. Potential e nergies o f covalent bonds and non-covalent interactions in n-alkyl ben zenes cy clized into t he position met a with respect to the substituent (co m mon a nd cyclized on CH3-). Calculated by the MM+ pr o gra m. For symbol s see text. n-alkyl benzenes (kJ/ mol) (nm) Methyl benzene Ethyl benzene n-Propyl benzene n-Butyl benzene n-Pentyl ben zene n-Hexyl benzene 7.06 8.96 10.86 12.76 14.66 16.56 0.25 0.25 0.25 0.25 0.25 0.25 –0.14 –0.13 –0.13 –0.13 –0.13 –0.13 –26.33 –26.92 –26.92 –26.92 –26.92 –26.92 14.85 39.73 42.78 45.77 48.96 52.14 0 0 0 0 0 0 0.59 0.72 0.82 0.95 1.06 1.19 3 Met hyl benzene Ethyl benzene Propyl benzene Butyl benzene Pentyl benzene 7.83 10.27 12.86 27.34 30.44 123.13 29.47 21.61 50.05 49.67 –3.58 –2.27 –1.06 2.48 0.98 194.74 292.85 305.63 185.38 –2.50 41.50 34.23 54.08 257.72 3102.9 0 0.56 0.24 0.16 0.13 0.47 0.51 0.57 0.62 0.66 in the intermolecular interactions and subsequently by a change in the relative retention time. The calculatio n results for the energies of the covalent bonds and non-covalent interactions are demonstrated for meta n-alkyl phenols (common and cyclized on CH3-) and n-al kyl b enzene s both c ommo n and c yclized i nto the meta position with respect to the substituent (again cy- cliz atio n thr oug h CH3-), are summarized in Table s 2 and 3. From Tabl es 2 and 3 it is evident that cyclization doe s not cause significant changes in covalent bonds, only small changes in electrostatic interactions and some ex- pected changes in the term was registred. How- ever , subst ant ial c ha nges too k p lace in the va n de r W aals interactions between the non-bonded atoms inside the molecules. Typical dependence of the van der Waals forces on the number of carbons ( ), shown in the ex- ample of para n-alkyl phenols, is pictured in Figure 3. This is of the similar character as the detected depend- ence of the logarithm of the relative retention time on (Figure 1, lines 3 and 4). This finding is in agreement with the fact that the same dependences were detected both in the cases of the polar and nonpolar phases and also in the cases of alkyl phenols and alkyl benzenes, because the retention data and their changes are in the given case related to intermolecular forces rather than to the structure of the compounds being considered. The similar results have been obtained in the case of ortho phenols cyclized on the -CH3 group and also in the case of the n-alkyl benzenes cyclized on the -CH3 group into ortho and para positions with respect to the substituent. Therefore, attention was focused on systematic calcula- tions of the energies of the van der Waals interactions. The numerical values of these energies showed the strength of the van der Waals forces; the results are summarized in Tables 4 and 5. From the data in these tables, it i s clear that the bi-linearity in these interactions occurs at (to be more specific when the phenol or benzene are substituted by n-propyl) during cyclization. However, this result was ascertained only for n-alkyl phenols and n-alkyl benzenes cyclized on the terminal methyl group. In the case of the -CH2- and -CH2-  P. STRAK A ET AL. Copyright © 2011 SciRes. AJAC 329 Table 4. Energies of van der Waals interactions ( , kJ /mol) in the molecules of n-alkyl phenols and n-alkyl benzenes. Calculated by the MM+ program. Positions “ortho”, “meta”, “para” at n-alkyl benzenes mean cyclization into the positions with respe ct to the substituent. Methyl phenol Ethyl phenol n-Propyl phenol n-Butyl phenol n-Pentyl phenol 17.12 41.25 44.24 47.23 50.40 14.57 39.44 42.49 45.48 48.66 14.60 39.47 42.51 45.51 48.69 Met hyl benzene Ethyl benzene n-Propyl benzene n-Butyl benzene n-Pentyl ben zene 14.85 39.73 42.78 45.77 48.96 14.85 39.73 42.78 45.77 48.96 14.85 39.73 42.78 45.77 48.96 3 Methyl phenol Ethyl phenol Propyl phenol Butyl phenol Pentyl phenol 11.39 12.09 27.61 49.25 210.20 32.45 95.81 385.1 3173 2942 44.96 109.4 411.3 1037 1132 3 Met hyl benzene Ethyl benzene Propyl benzene Butyl benzene Pentyl benzene 10.40 11.23 14.25 27.64 64.51 41.50 34.23 54.08 257.7 3103 23.99 46.87 67.42 339.3 832.2 Table 5. Energies of van der Waals interactions ( , kJ /mol) in the molecules of n-alkyl phenols and n-alkyl benzenes. Calculat ed by the A MBER pr o gra m. Positio ns “ortho”, “meta”, “para” at n-alkyl benzenes mean cyclization into the positions with respect to the substituent. Methyl phenol Ethyl phenol n-Propyl phenol n-Butyl phenol n-Pentyl phenol n-Hexyl phenol 17.54 36.17 36.54 37.13 37.90 38.71 13.53 35.04 35.48 36.07 36.86 37.67 13.58 35.09 35.53 36.13 36.91 37.72 Met hyl benzene Ethyl benzene n-Propyl benzene n-Butyl benzene n-Pentyl ben zene n-Hexyl benzene 13.90 35.43 35.87 36.48 37.26 38.07 13.90 35.43 35.87 36.48 37.26 38.07 13.90 35.43 35.87 36.48 37.26 38.07 3 Methyl phenol Ethyl phenol Propyl phenol Butyl phenol Pentyl phenol 14.93 11.05 19.08 38.38 703.1 43.83 141.6 2976 4*106 4*106 10 65.28 175.1 6247 9*104 - 3 Met hyl benzene Ethyl benzene Propyl benzene Butyl benzene Pentyl benzene 12.92 14.35 11.52 16.90 61.29 55.41 40.43 61.62 1083 6*106 24.34 53.46 74.65 4183 35913 cyclizations, the detected values were si milar to common n-alkyl phenols and n-alkyl benzenes and no relevant dependences on were found, as stated above. An increase in the van der Waals interactions inside the cyclized molecules (i.e. intramolecularly) must also be reflected in an increase of the forces between mole- cules (i.e. intermolecular ly). A more intense e ffect of the attraction forces between molecules should then manifest itself through a corresponding increase of the boiling temperatures of the C9-compounds and be higher in both types of molecules in question. The increase of the in- termolecular forces caused by cyclization was confirmed by a comparison of the boiling points of normal (–42.1˚C - 125.5˚C) and alic yclic (–33.5˚C - 150˚C) hydrocarbons C3-C8. The results are shown in Table 6. The values of the boiling p oints were taken fro m the co mpendium [14] and verified against the compendium [15]. From the values shown in Table 6, it is evident that the boiling points of alicyclic hydrocarbons increase with the num- ber of carbons in the molecule similarly to van der Waals forces. If a change in the relative retention time as a result of cyclization is caused by a change in the size of the mo- lecule moving in a chromatographic column and a chan ge i n bo th intr a mole c ula r a nd inte r mol ecula r van de r Waals forces, then the related cyclization of the alkyl chain could really be, in the case of n-alkyl phenols, ac- companied by the formation of a hydrogen bridge be- tween the oxygen in the phenolic group -OH and a hy- drogen of the terminal group -CH3 of the alkyl; in other words, in the case of n-alkyl phenols, the tendency to form hydrogen bridges resulting in a heterocyclic ring with six or more members being formed including also one C-C bond of the aromatic ring of phenol as shown in Figure 2 could actually be considered. Similarly, in the case of alkyl benzenes, a tendency to integrate could exist between the benzene ring ( ) and a hydrogen of the terminal group -CH3 of the alkyl ( ), resulting in the formation of a five-membered or more-membered ring, i ncl ud i ng al so o ne C -C b o nd o f t he a r o ma tic r i ng of benzene (Figure 2). F rom the thermodynamical aspect, it  P. STRAK A ET AL. Copyright © 2011 SciRes. AJAC 330 Table 6. Boiling points ( ) of normal and alicyclic hydro- carbons C3–C8 and energies of intramolecular van der Waals interactions. Alkane (˚C) (MM+) (kJ/mol) (AMBER) (kJ/mol) Cyclooctane 150 501.1 7840 is the affinity of these low-molecular compounds to the stationary high-molecular phase that is important when they are being mixed with this phase. The degree of af- finity is the change in the Gibbs free energy of mixing when the molecules of alkyl phenol or alkyl benzene are blended with high-molecular chains or molecules of the stationary phase ( ) at constant temperature and pressure: 0 mix mixmix GH TS∆=∆−∆ < (1) where mix H∆ is the enthalpy of mixing, mix S∆ the entro p y of mi xing a nd the temperature of the separa- tion ( K). T he more negati ve the mix G∆ is, the better the mixing of the compounds will be (for the stationary phase). Since the entropy of the system always increases when the components are mixed, and the entropic term of the Equation (1) is thus always negative (mix TS−∆ < 0), the mixing/solubility depends mainly on the value of mix H∆. The thermodynamic condition of the solubility of a low-molecular element in the statio- nary phase , or the mixing of the two subst ances is then: (2) The blending will thus be the best in the case mix H∆ , when also the solubility of one component in the other will be maximal as well. However, this is an ideal case. The parameters of the solubility were intro- duced for practical purposes, numerically characterizing the solubility of low-molecular and high-molecular sub- stances [16]. A lo w-molecular substance with a so lub ility parameter identical to the solubility parameter of the high-molecular substance will achieve maximal dissolu- tion during the mixing, because in this case. Since cyclization increases δ in the case of hydrocarbons, e.g. in the ca se o f hexan/cyclohexan fr om 14.9 (hexan) to 16. 8 (cyklo hexan) [ 17], the mixing is improved, because this parameter for the high-molecular stationary phases [18] can be approximately 16 - 18. Cyclization th us faci- litates the mixing of al kyl phe nols or alkyl b enze nes wit h high-molecular stationary phases, because the thermo- dynamic condit ion for mixing is better fulfilled. On the whole, the data obtained can both serve an analytical methodology for the analysis of aromatics and phenolics, which is still being discussed [19], and pro- vide deeper insight into the problem of the van der Waals forces/non-covalent interactions, which is also a topic of interest [20] . 4. Conclusions The side alkyl chains of n-alkyl phenol s beco me cyclized in both the polar and nonpolar stationary phases of ca- pillary columns, with a possible formation of hydrogen bridges between oxygen of the phenolic OH group and hydrogen of the methyl group of the side alkyl chain. In the case of n-alkyl benzenes, cyclization is made possible because of the interaction between benzene ring ( ) and hydrogen of the terminal methyl group ( ) of the alkyl chain. In the case of the formed aromatic-quasi- alicyclic molecules, the effect of the van der Waals forces thus increases not only intramolecularly but also intermolecularly. In the case of n-alkyl phenols and n- alkyl benzenes this effect is strong with the molecules having the number of carbons higher than nine. This re- sults in bi-linearity in the retention characteristics of these compounds, observed in the dependence of the logarithm of the relati ve retention time on the total num- ber of carbons in the molecule. 5. Acknowledgements This work was supported by the Grant Agency of the Academy of Sciences of the Czech Republic in the fra me of project No. IAA300460702 a nd the Institute Research Plan, Identification Code AVOZ30460519. 6. References [1] P. Buryan and J. Macák, “Partial Explanation of the Anomaly in the Relationship between the Logarithm of Retention and the Carbon Number of Monohydric Phe- nols,” Journal of Chromatography A, Vol. 237, No. 3, 1982, pp . 381-388. doi:10.1016/S0021-9673(00)97624-6 [2] H. Purnell, “Gas Chromatogr aphy,” John Wiley and Sons Inc., New York, 1962. [3] E. Leibnitz and H. G. Struppe, “Handbuch der Gas- Chromatographie,” AVG & Portik K.-G., Lepzig, 1966. [4] G. Guiochon, “Retention Indices in Programmed Tem- perature Gas Chromatography,” Analytical Chemistry, Vol. 36, N o. 3, 19 64, pp. 66 1-663. doi:10.1021/ac60209a034 [5] W. E. Hartus and H. W. Habgood, “Programmed Tem-  P. STRAK A ET AL. Copyright © 2011 SciRes. AJAC 331 perature Gas Chromatography,” John Wiley an d Sons Inc., New York, 1966. [6] C. Simpson, “Gas Chromatography,” Kogan Page, Lon- don, 1970. [7] P. Straka, P. Buryan and J. Nahunkova, “Possibil ities of Cyclization of Side Alkyl Chains of n- Alkyl Phenols and n- Alkyl Benzenes in the Environment of a Stationary Phase,” Acta Geodynamica et Geomaterialia, Vol. 5, No. 1 (149), 2008, pp. 65-76. [8] P. Straka, “Chemical structure of coal substance,” Acta Monta na Se r ies AB, No. 12(132), 2003, pp. 7-47. [9] G. A. Carlson, “Computer Studies of Coal Molecular Structure”, Proceedings 1991 International Conference on Coal Science, Newcastle upon Tyne, September 1991, pp. 24-27. [10] A. C. T. van Duin and J. S. S. Damsté, “Computational Chemical Investigation into Isorenieratene Cyclisation,” Organic Geochemistry, Vol. 34, No. 4, 2003, pp. 515- 526. doi:10.1016/S0146-6380(02)00247-4 [11] A. Howard, J. McIver and J. Collin s, “HyperChem Com- putational Chemistry,” Publishing HC40-00-03-00, Hypercube Inc., Waterloo/Onta r io/Ca na da , 1994. [12] U. Becker and N. L. Allinger, “Molecular Mechanics,” American Chemical Society, Monograph 177, Washing- ton D. C., 1982. [13] N. L. Allinger and Y. H. Yuh, “Quantum Chemistry Pro- gram Exchange,” Indiana University, Bloomington, 1982. [14] Collective of authors, “Spravotschnik Chimika, Osnov- nyje Svojstva Neorganitcheskich I Organitcheskich Soje- dinenij,” Gosudarstvennoe Nautschno-Technitscheskoe Izdatelstvo Chimitscheskoj Literatury, Moskva, 1951. [15] M. Vecera, J. Gasparic, J. Churacek and J. Boreck y, “Ch- emical Tables of Organic Compounds,” SNTL-Technical Literature Publis hing House, Praha, 1975. [16] J. H. Hildebrand and R. L. Scott, “Solubility of Non- Electolytes,” Reinhold publishing company, New York, 1959. [17] J. Brandrup and E. H. Immergut, “Polymer Handbook,” John Wiley and Sons Inc., New Yo rk, 1975. [18] J. Mleziva, “Polymery,” Sobotales Publishing industry, Praha , 1993, p. 46 7. [19] M. Naczk and F. Shahidi, “Extraction and Analysis of Phenolics in Food,” Journal of Chromatography A, Vol. 1054, No. 1-2, 2004, pp. 95-111. [20] P. Hobza, R . Zahradni k, K. Müller-Dethlefs, “The World of Non-Covalent Interactions: 2006,” Collection Cze- choslovak Chemical Communications, Vol. 71, No. 4, 2006, pp . 443-531. doi:10.1135/cccc20060443
|