Journal of Geoscience and Environment Protection, 2015, 3, 35-47
Published Online July 2015 in SciRes. http://www.scirp.org/journal/gep
http://dx.doi.org/10.4236/gep.2015.35005
How to cite this paper: Guo, Z.W., Dong, H.F. and Xiao, J.P. (2015) Detection of Permafrost Subgrade Using GPR: A Case
Examination on Qinghai-Tibet Plateau. Journal of Geoscience and Environment Protection, 3, 35-47.
http://dx.doi.org/10.4236/gep.2015.35005
Detection of Permafrost Subgrade
Using GPR: A Case Examination
on Qinghai-Tibet Plateau
Zhenwei Guo1*, Hefeng Dong1, Jianping Xiao2
1Department of Electronics and Telecommunications, Norwegian University of Science and Technology,
Trondheim, Norway
2The Institute of Geoscience and Info-Physics, Central South University, Changsha, China
Received 31 March 2015; accepted 10 July 2015; published 17 July 2015
Abstract
In the Qinghai-Tibet railway ballast exploration, the main purpose is to detect frozen disease by
Ground penetrating radar (GPR). New special GPR equipment was tested for the Qinghai-Tibet
railway ballast exploration. For frozen disease detection on railway ballast, GPR has high resolu-
tion and efficient advantages compared with other geophysical methods. It is essential guaranteed
to improve data processing accurately and effectively. In this paper, we employ predictive decon-
volution methods to remove multiples to enhance signal noise ratio. Permafrost physical proper-
ties were studied, so that permafrost recognition algorithm would be given to detect frozen dis-
ease. Firstly, we test this algorithm at Central South University by GR-III GPR, where the results
were shown an effective and efficient GPR equipment and permafrost recognition algorithm cho-
sen. According to simulation of the geological data of the typical testing section of Qinghai-Tibet
railway, predictive deconvolution method could remove most of multiples from synthetic data. At
the end, we explored the permafrost on Qumar area on the Qinghai-Tibet highland. A high quality
interpretation was given after the data processing.
Keywords
Ground Penetrating Radar, Qingh ai-Tibet Railway Ballast, Perm af ros t, Predictive Deconvolution
1. Introduction
Permafrost is the unique problem with which Qinghai-Tibet railway is confronted. One fifth of the global land
masses are underlain by permafrost (French, 1996) [1] . Annual thawing and freezing of ground underlain by
permafrost has major impact on the ground properties (French, 1996; Williams and Smith, 1989) [1] [2]. With
the future scenarios of climate change, the dynamic response of permafrost is a major concern. Subgrade in
permafrost region varies according to the temperature.
*Corresponding author.

Z. W. Guo et al.
36
Serious difficulties of the railway construction, operation and maintenance are brought by the special condi-
tions of the Qinghai-Tibet railway. In order to guarantee safe operation of the Qingha i -Tibet railway, ballast
sacks, contaminations, moist areas, packed layers and permafrost must be located and monitored continuously. It
is important to understand how these ice masses and the frozen ground are influenced by the predicted climatic
forcing and feedback mechanisms such as: changes in albedo, thermal and mechanical properties, melting of ice
and changes in water path ways. Therefore, there is a need to detect and map such ice and permafrost features,
both in space and over time in order better to understand their dynamics and behavior (Kääb, 2005) [3].
Ground Penetrating Radar (GPR) is a remote sensing method that has been used extensively in investigations
for inspection of railway tracks (Gobel, et al. 1994) [4 ] and as a geophysical method in permafrost research to
map subsurface structures and composition (Moorman et al., 2003 and references therein) [5]. Frozen ground is,
in general, GPR “friendly” with low energy dissipation and a good potential for large depth penetration, the pos-
sibility of mapping the subsurface geometries and internal structures (Arcone, 2002; Daniels, 2004) [6] [7]. In
recent years the potential of using GPR surveys on other planetary bodies, such as on Mars, has increased
awareness and research on the performance of GPR over frozen ground (Arcone, 2002) [6]. Nevertheless, the
success of GPR studies on frozen grounds, such as sediments and tills, is sometimes limited due to diffi culties in
data interpretation and information extraction (Irvine-Fynn, 2006) [8].
In this paper, a permafrost recognition algorithm is introduced, which is especially designed for the perma-
frost sediments. This algorithm is applied to a set of measured data for detection of the permafrost ballast. It is
demonstrated that the permafrost recognition algorithm is a reliable and effective method.
2. Site Location and D escription
In Qinghai-Tibet Plateau, the natural conditions are harsh, the air is oxygen-poor and the climate is bitterly cold.
Most of the land consists of mountains, wilderness, and permafrost and snow zones. This study site is located at
the northeast of Hohxil (Figure 1), which is within a region of permanent permafrost. The mean annual air tem-
perature in Qumar is −4˚C. The study area, which is subjected to the test section in the Qin ghai -Tibet railway, is
located above Qumar high plains. The height of the ballast is 6.3 m, and the width of pavement is 8.3 m, while
the berm width around both sides is 3.0 m. Conglomerate and sandstone are filled about 30 cm under the base of
ballast, at the same time, 4% of the cross-slope, along both sides of the filling-based centers, is necessary. Sliced
stones and rocks, which have a thickness of 1.5 m, are filled above the conglomerate and sandstone. At the top
of the sliced rock chip a layer of gravel in a round cushion was built and its thickness is 30 cm, which is a layer
of an impermeable layer on the laying of sand-gravel cushion, while the ballast is filling with coarse soil (Xiao,
2009; Guo, 2010) [9] [10].
3. Geological and Geographical Setting
These marlstones are of alluvial origin, their thickness ranges from 2.1 m to more than 5.5 m and they are
Figure 1. Location of the study area.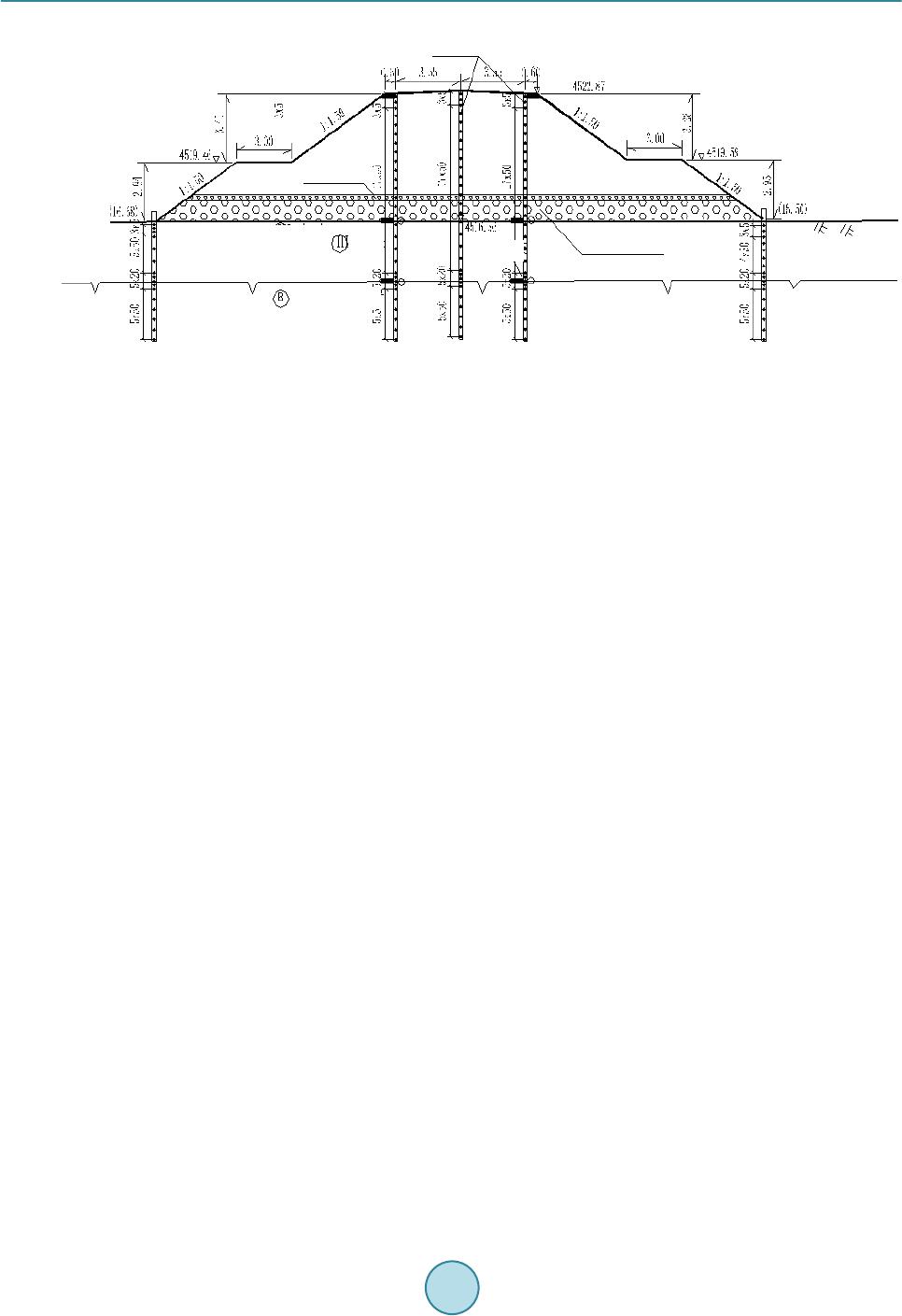

Z. W. Guo et al.
37
Figure 2 . Geological model of ballast.
covered by sandstones at a regional scale. The sandstones appear as layers of finely sorted sandstones of colors
ranging from yellow brown to brown. Spectrographically speaking the sandstones is composed of quartz grains
marginally associated with feldspars. Above the layers there are conglomerate and sandstone joints of sliced
stones that can reach 30 centimeters in thickness. Some marlstones layers show abundant frozen sedimentary
traits of cross layered stratification in which the volume has a 40% - 90% ice content.
4. Permafrost-GPR Elucidation
All geologic materials exhibit lower electrical conductivities frozen than thawed due to the absence of liquid
water, implying a good potential use of GPR as a remote sensing instrument to map frozen ground properties
(Guo , 2010a) [10]. In highly (none frozen) conductive media the electromagnetic (EM) waves emitted by the
GPR will be absorbed, leading to shallow penetrating depths. In the literature there are a number of different de-
finitions of permafrost but a common one is ground with a temperature below 0˚C for at least two consecutive
years (French, 1996) [1]. This definition is not always practical from a GPR perspective, due to the fact that
water freezes in the ground at a range of temperatures at or below 0˚C, depending on the soil properties (Hans-
son, 1988) [11]. It should therefore be kept in mind that what in general terms is called permafrost can contain a
significant degree of unfrozen soil with free liquid water. This can lead to substantially higher conductivity and
thus larger loss of the EM waves and large differences in permittivity contrasts, despite the fact that the ground
temperature is below 0˚C and is defined as permafrost (Brandt and Langley, 2007) [12].
5. GPR Data Collection and Processing
We used a GR-III Ground Penetrating Radar with different antennas to map the buried frozen and melted sedi-
ment. Both systems are impulse radars. The GR-III unit was operated with the shielded 100, 200 and 400 MHz
antennas.
The GPR profiles were run in a common offset mode. The center frequencies of the detection used are 100,
200 and 400 MHz, for 1024 sampling points, sampling rate of 1024 - 1706 MHz, which is 10 - 17 times more
than the antenna center frequency. Data were collected with a 5 ns range and 1024 samples per scan. When the
depth is less than 15 m, the permittivity of the layer is between 6 and 13. Thus, one wave velocity in typical
permafrost layer is limited between 0.08 and 0.15 m/ns. Therefore, the time window is chosen as 60 - 300 ns.
The antennas were towed by people (to keep external radio noise low), with antennas mounted in plastic box-
es to avoid interference with nearby metal objects. The different antennas were driven along the same tracks,
with common start and stop points. The start and end positions were determined with a GPS code receiver.
The GPR data were, after the survey, directly low- and high-pass filtered, and post-processing consisted only
of 1) block average smoothing, 2) down-sampling the traces to 1024 samples using linear interpolation (to avoid
on-screen display aliasing), 3) two fold stacking and 4) applying a linear time-varying gain. Background signal
removal to remove constant instrumental noise, antenna ringing and to suppress the direct wave has been per-
Ground
1.5 m Sliced rocks
30 cm conglomeates
Sandstone
Marlstones
Frozen boundary
Temperature measurement
Permafrost Surface

Z. W. Guo et al.
38
formed by subtracting a weighted part of the average trace (calculated using all traces) from the profile (hereaf-
ter referred to as “background removal”). The weight has been set lower in profiles containing long and flat ref-
lections to avoid subtracting valuable information.
The GR-III data required more processing. It has been low- and high-pass filtered using a zero-phase filter,
both in the forward and backward direction. The data also contained different DC (low frequency voltage offset)
trends both in the individual traces and along the profiles. These DC shifts have been removed by calculating a
trimmed mean within the data (the mean calculation to avoid weighting of the data by extremes), and subtracting
it from the data. In addition to linear time-varying gain, an adaptive gain control has also been used for display
purposes to additionally enhance weak reflections which are still above the noise floor. This gain control calcu-
lates the standard deviation of the data and the gain is a weighted function of the standard deviation. The GPR
profiles have not been elevation corrected because the area is flat compared to the GPR profile lengths and pe-
netration depth.
6. Methods
6.1. Calculation of EM Wave Velocity and Depth
The GPR reflections were verified where possible with shallow auger holes, sediment cores, ice cores and water
depth measurements. From these data, both the calculated radar depth and the radar velocity were determined.
To convert two-way travel time to depth, we developed a multilayer model. The latter increases the accuracy of
depth estimations when radar waves travel through multiple layers, each with a different velocity. The multi-
layer depth calculation was derived from:
1
2
nii
Ti
tv
D
=
∗
=
∑
(1)
where DT is the total depth (m), i is the interface number, vi is average propagation velocity (mns − 1) from in-
terface (i − 1) to interface (i), and ti is the two-way travel time (ns) from interface (i − 1) to interface (i). The
difference in the GPR signal response was determined by the reflection coefficient. Using the dielectric con-
stants, an estimation of the reflection coefficient for an interface under vertical incidence can be determined
from:
12
12
Rkk
kk
−
=+
(2)
where R is the reflection coefficient, k1 is the permittivity of the overlying material and k2 is the permittivity of
the underlying material (A-CUBED, 1983) [13] . The dielectric constants for ice (k = 3), water (k = 80) and fro-
zen sediment (k = 7.5) are calculated by:
()
2
kcv =
(3)
where c is the velocity of the EM wave in free space (m∙ns−1) and v is the measured wave velocity through the
low loss material (m∙ns−1).
6.2. Permafrost Recognition Algorithm
6.2.1. Log Power Spectrum
For a given signal x(t), whose spectral density P(ω) is non-negative and even symmetry, the power spectrum
2
()P ω
highlights the main component of
() 1P ω >
,which suppresses those the minor of
() 1P ω <
. Thus it
is benefited for the power spectrum to highlight and identify the main features of the spectrum. The log-power
spectrum could use to identify several features of the power spectrum, which is defined as:
( )
2
lg( )
xx
LP ωω =
(4)
The GPR signal collection is a result of sub-waves and the formation reflection coefficient convolution, so the
power spectrum of the radar data is the stratigraphic sequence of the power spectrum and the reflection coeffi-
cient of the radar wavelet power spectrum multiplied by the results of operations. Using the operations of loga-
rithm, the information of spectrum can be translated into the superposition of stratum and the wavelet power

Z. W. Guo et al.
39
spectrum. It is convenient for us to observe that the stratum makes the transform of the frequency response in
the radar wavelet.
6.2.2. Time Window Selection
To study the radar cross-section of road-based diseases, we hope the road only to be the spectral data of the basis,
so the time window is necessary on the time profile of the radar in order to analyze the localized features of the
spectrum which the time signal on the basis of partial section is corresponding to.
The function which has the window features satisfied the following qualification.
( )
2
ˆ
ω,()( )Gtg tLR ω ∈
(5)
where g(t) is the time window function,
( )
ˆ
G ω
is the result of Fourier transform of g(t).
Many functions can be used as the time window function, such as Rectangular function, Yamagata functions
and m-splines and so on. However, the selection of window function must be based on the “uncertainty principle”
in order to achieve time and frequency domain localization of the highest resolution. “Uncertainty principle” is
given: For the window function g(t), its window size to meet the following formula.
( )
ˆ
4 g(t)2G ω ∆∆ ≥
(6)
Only when g(t) is Gaussian function can the Equation (6) be defined. Gaussian window is the best window for
partial analysis, which is defined as:
( )
2
4
1
2
x
gx e
σ
σ
πσ
−
=
(7)
6.2.3. Construction of Rolling Spectral Profile
As the ground-penetrating radar to obtain the real signal, while the real value of the signal spectrum is symme-
tric, we take a positive semi axis part of the frequency analysis. At the beginning of time window, because of the
radar reflectivity profile, there is a ground-penetrating radar as an arbitrary mapping relationship:
( )
1
0
1
00 0
x() W(T)lg()
N
n
Pn
N
t tQt
ω
−
=

∆


→+∆ →→
(8)
where,
0
()xt
is that the time profile corresponds to 0 time information;
0
()Wt T+∆
is the selected time
window between
00
t ~(tT) +∆
;
( )
1
0
1
lg
N
n
Pn
N
ω
−
=

∆


is the discrete spectrum which the time profile is in the
00
~( )ttT+∆
time window; Δω is the frequency interval;
0
()Qt
is the mean spectrum of discrete spectral
values which corresponds to:
()
()
1
00lg Pn
NN
n
Qt n
ω
ω

∆


=


= ∗∆


∑
(9)
On the time profile, the radar reflection time t0 is expressed by the energy conversion for a given time window
of the rolling average spectra of
0
()Qt
.
If
T∆
is the time interval from the starting point along the time-depth, a rolling cross-section could be de-
fined as the mean spectrum of type (9). It is scrolled down to the depth at each time point corresponds.
()( )
()
0
G ()
m
T
t
mQt m
=
=
∑
m = 1-Sample Points (10)
TM is the sampling time window.
6.2.4. The Improvement of Scroll Spectrum Algorithm
There are some problems as follows, if we adopt the Equation (10) to calculate the rolling spectral profile.
Computer is running slow. Radar detection is a fast method to detect. When the data interpretation is processed,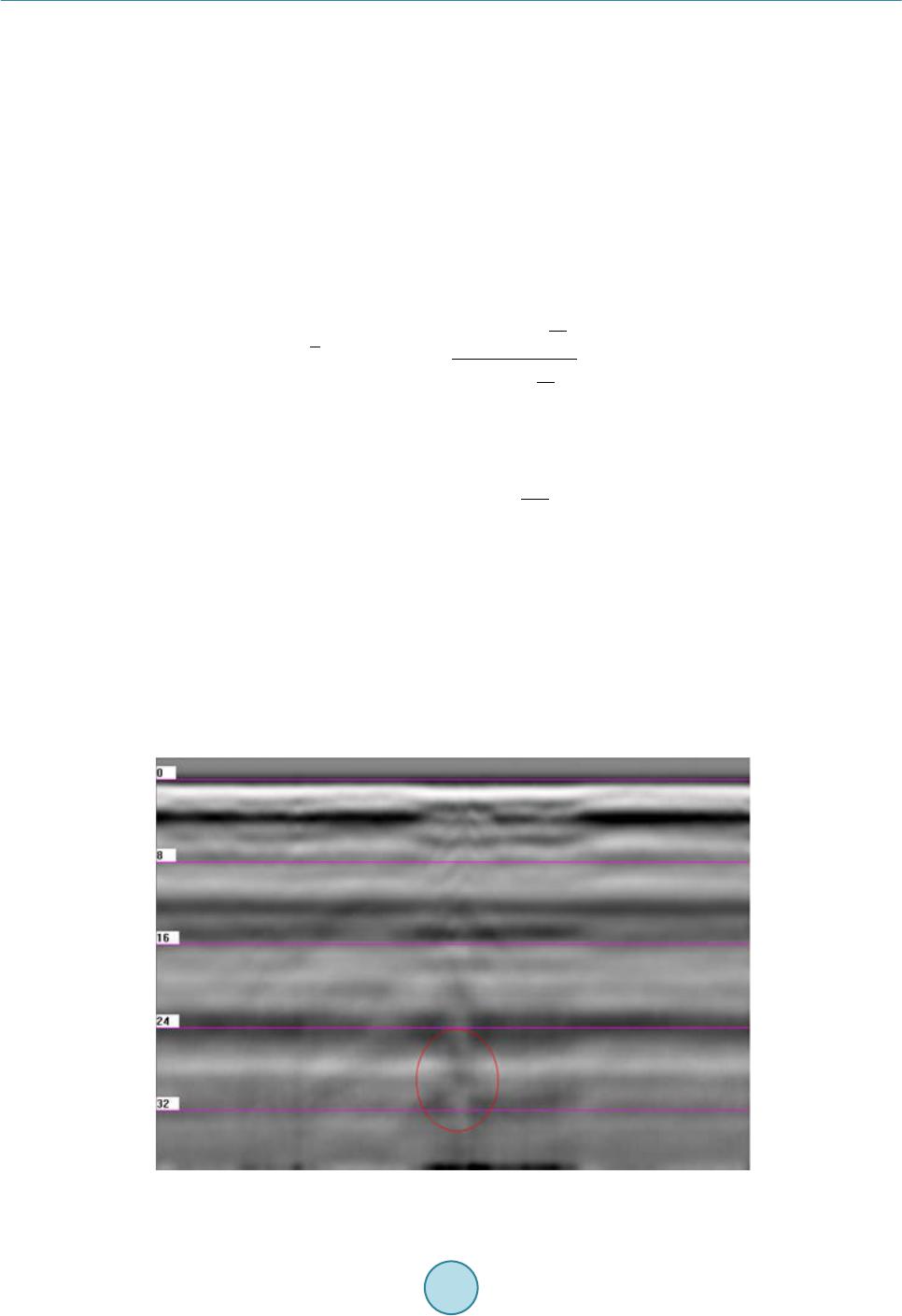

Z. W. Guo et al.
40
using complicated time algorithm to obtain results, the effectiveness of radar detection will be hugely impacted.
It is vulnerable to be interference in the signal mutation. Ground Penetrating Radar detects by the use of emis-
sion and reflection of electromagnetic waves. It is susceptible to be interference, so how to reduce the impact of
interfering signals, it is significantly irreplaceable to the ultimately results in the data interpretation.
For these reasons, scroll spectrum algorithm needs to be improved. First, it is necessary to multiply the fre-
quency of rolling scan by N, by controlling the size of the N values to achieve fast computation purposes. If the
original sampling points were 512, 512 times of the mean spectrum need to be computed for each of trace; if N
takes 8, only 64 times of the mean spectrum need be computed, and computation time is increased eight-fold.
Equation (10) by rolling multiple becomes:
()
()
()
G ()
m
tT
tiNT
mQtN im
≤
= ∗∗∆
= +∗
∑
(11)
Secondly, by Equation (11) the number of secondary sample is resumed.
()
( )
()
0
sin
()
m
Ts
t
s
tm T
GmGm tm T
π
π
=

−∗


=
−∗
∑
(12)
m = 1-Sample Points.
Finally, the results of the second sample will be filtered by the sliding windows opening two-dimensional fil-
tering.
()
ˆ
NM
mn
nN nM
Gm G
=−=−
=
∑∑
(13)
where n and m are the number of the traces and sample points, respectively.
6.2.5. Effect of Rolling Spectrum Algorithm
In order to make sure the algorithm effectively and efficiently, we tested the rolling spectrum algorithm on the
data measured by Italian radar, SIR series at a lawn area inside the Central South University, which furnished
watering piper underground. Figure 3 is the image of the area. Due to the underground soil moisture larger in
the lawn area than others area, the soil has a strong absorption of electromagnetic waves. It is shown that it is
very difficult to find an existing exception by the Italian radar. Figure 4 shows the result of the adoption of rec-
ognition algorithms, unusual features to be strengthened.
Figure 3. Time profile image.

Z. W. Guo et al.
41
Figure 4. ARM A Lo g-power spectrum profile.
6.3. Deconvolution and Prediction Deconvolut ion
Deconvolution is one of the most used techniques for processing seismic reflection data and GPR data. It is ap-
plied to improve temporal resolution by wavelet shaping and removal of short period reverberations, (Robinson
and Treitel, 1980; Yilmaz, 1987; Leinbach, 1995) [14]-[16]. As an assumption, a seismic trace x(t) results from
the convolution of a basic wavelet p(t) with an uncorrelated series n(t), where we assume that n(t) can be identi-
fied with the reflection coefficient series of a layered medium (Robinson,1954; Robinson,1957) [17] [18],
( )( )
xtp tn(t)= ∗
(14)
Since the desired out is an impulse at zero lag time, we deem that the model requires a filter f(t) such that,
( )( )
ft pt1∗≅
(15)
Or,
()( )
1
ft pt
−
≅
(16)
where the symbol
≅
means “approximately equal to”. The filter f(t) then deconvolves the input trace as fol-
lows:
()() ()()( )( )
1
ytxt ftpt ptnt
−
≅∗≅∗ ∗
(17)
( )()( )()
yt δt ntnt≅∗=
(18)
where
( )
δt
is the Dirac’s delta function, which is a unit impulse function and in this sense the output trace
tends to approximate the subsurface reflection coefficient series.
In the predictive deconvolution, given the input x(t), we want to predict the value at a delayed time x(t + α),
where α is the prediction lag. In the predictive deconvolution process, we have to specify the operator length n
and the prediction lag α. The main motivation for using predictive deconvolution in seismic processing is to at-
tenuate multiples. Figure 5 shows the result of predictive deconvolution for one trace.
To find n and α we use a so-called parameter test process, from which it is possible to decide which values of n
and α should be chosen, based on the autocorrelation. Based on ballast geological model (Figure 2), we simu-
lated GPR traces as illustrated in Fig ures 6-9 are the results of predictive deconvolution with different parame-
ters. For α we test the values of 70, 140 and 300, while for n we test the values of 200, 300 and 400. Typical pa-
rameter test plots are provided in Figure 7.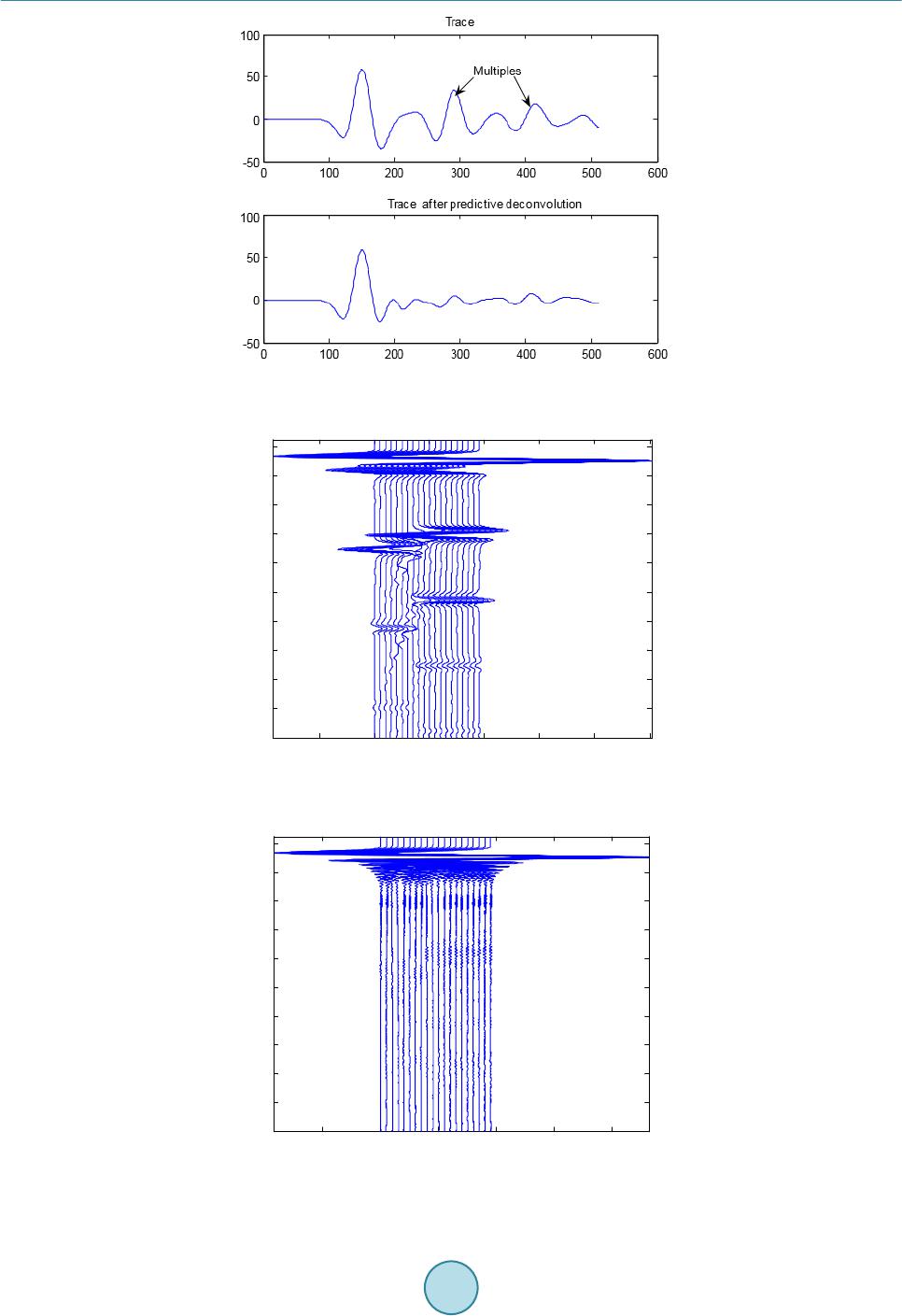

Z. W. Guo et al.
42
Figure 5. Comparison of the result of predictive deconvolution
with the oriental trace
Figure 6. Numerical simulation of bridge model.
Figure 7. Predictive deconvolution result of α is 70.
-1 012345
x 10
4
200
400
600
800
1000
1200
1400
1600
1800
2000
-1 01234
x 10
4
200
400
600
800
1000
1200
1400
1600
1800
2000

Z. W. Guo et al.
43
Figure 8. Predictive deconvolution result of α is 140.
Figure 9. Predictive deconvolution result of α is 300.
Based on the parameter testing, we choose α = 140 and n = 400 as the input parameters to the process. The
conclusion of the deconvolution is that the multiples are attenuated, see Figure 8, and the signal of the reflec-
tions of the subsurface becomes clearer.
7. Example
7.1. GPR Modelling
In the geological radar detection range down, the measurement regions are parts of the backfill areas, from the
main formation include (Figure 2) six layers.
A multilayer permafrost model is given for simulation. From top to bottom, the media are air, the ballast filled
with coarse soil, marlstones, sandstone, conglomerate and sliced rocks. The physical parameters of each medium
are given in Table 1.
We employed the GR-III operated with the shielded 200 MHz antenna. The GPR profiles were run in a com-
mon offset mode. The center frequency of the detection used is 200 MHz, for the 1024 sampling points, sam-
-1 012345
x 10
4
200
400
600
800
1000
1200
1400
1600
1800
2000
-1 012345
x 10
4
200
400
600
800
1000
1200
1400
1600
1800
2000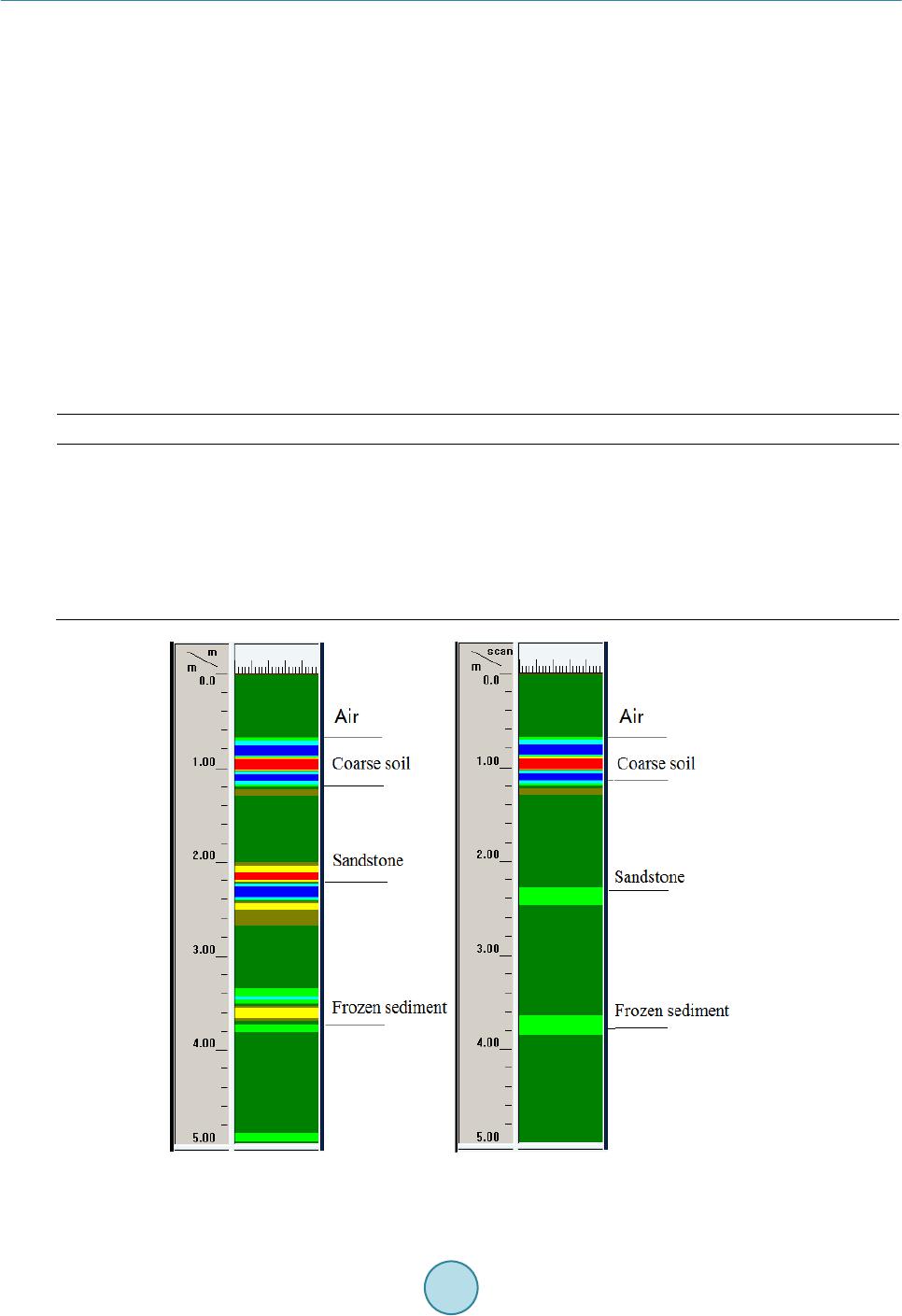

Z. W. Guo et al.
44
pling rate of 1024 - 1706 MHz, which is 10 - 17 times more than the antenna center frequency. Figure 10 de-
picted GPS simulation result and after predictive deconvolution processing.
7.2. Real Data Inversion
The study area, which is tested on the Qinghai-Tibet railway, is located above Qumar high plains. The geologi-
cal information has been given in section 2. In the geological radar detection range down, the measurement re-
gions are parts of the backfill areas. The main formation includes three layers as shown in Figure 11: the first
layer: 0 - 4 m, the second layer: 4 - 8.6 m, and the third layer: 8.6 - 12 m.
For more information on the shallow depth strata is detected by 200 MHz and 400 MHz antenna, its initial
results are shown in F igure 12 and Figure 13 (Xiao, 2009; Guo 2010a) [9] [10]. An interface is located at the
depth of 0.7 m, which is located the true ranges between 0.66 m and 1.1 m. The sand covering is judged affirma-
tively. The thick layer, with a preliminary judge for the relatively small amount of an ice freeze-thaw zone, con-
tinuously varies between 0.7 m and 1.3 m in depth. The layer from 1.3 m to 2.58 m in depth, with a thickness of
ups and downs, is initially judged to contain more ice than the freeze-thaw zone. The permafrost sediments are
believed in the depth of 2.58 meters to 4 meters (Guo, 2010b; Guo, 2010c) [19] [20].
Table 1. Physical parameters of each layer in realway ballast.
Media Permittivity Velocity (m/ns) Thickness (m)
Air 1 0.3 0.4
Coarse soil 5 0.13 0.85
Marlst o nes 9 0.1 1.75
Sandstone (unfrozen) 30 0.05 1.7
frozen sediment 6 0.12 0.8
Conglomerate and sliced rocks 5 0.13 1.8
Figure 10. GPR Simulation (left) and Predictive deconvolution (right) result for
200 MHz antenna.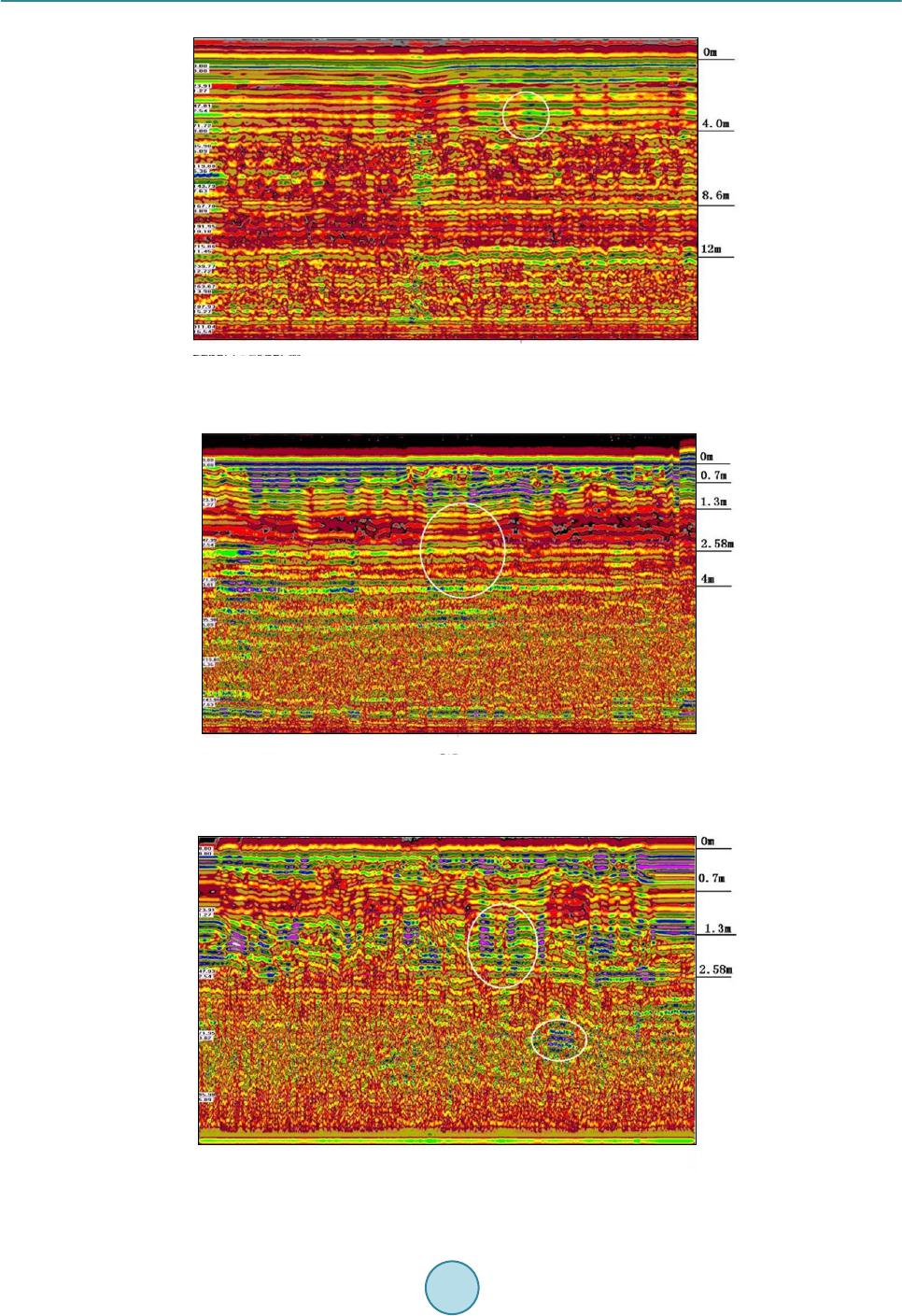

Z. W. Guo et al.
45
Figure 11. GPR data inversion result in 100 MHz case.
Figure 12. GPR data inversion result in 200 MHz case.
Figure 13. GPR data inversion result in 400 MHz case.
Trace
0.00
23.91
47.01
71.72
95.98
119.88
143.79
167.70
191.95
215.86
239.77
263.67
287.53
311.84
Times
Trace
0.00
23.91
47.99
71.89
95.98
Trace
0100 200 300 400 500 600 700 800 9001000
0.00
23.91
47.93
71.95
95.98
Times

Z. W. Guo et al.
46
8. Conclusion and Im plica tions
The results show that basic multi-frequency GPR techniques can be valuable for detection and mapping of bu-
ried ice as well as for revealing structures and the make-up of permafrost sediments. Information collected by
the dedicated GPR system is valuable for preventing severe hazard to railway traffic and planning renovation.
Furthermore the possibility of optimizing the location of drill spots and surveying without closing the tracks
makes this method of investigation appreciable.
Acknowledgements
The authors would like to thank the Ministry of Science & Technology of China for the financial support of Na-
tional Key Project of Scientific and Technical Supporting.
References
[1] French, H.M. (1996) The Periglacial Environment. 2nd Edition, Addison-Wesley-Longman, Reading.
[2] Williams, P.J. and Smith, M.W. (1989) The Frozen Earth—Fundamentals of Geocryology, Studies in Polar Research,
Cambridge University Press.
http://dx.doi.org/10.1017/CBO9780511564437
[3] Kääb, A. (2005) Remote Sensing of Mountain Glaciers and Permafrost Creep. Geographisches Institut der Universität
Zürich. Stiftung Zentralstelle der Studentenschaft der Universität Zürich, Vol. 48.
[4] Gobel, C., Hellmann, R. and Petzhold, H. (1994) Georadar Model and In-Situ Investigations fo r Inspection of Railway
Trac ks . Proceedings of Ground Penetrating Radar Conference, Kitchener, 12-16 June 1994, 1121-1133.
[5] Moorman, B.J., Robinson, S.D. and Burgess, M.M. (2003) Imaging Periglacial Conditions with Ground Penetrating
Radar. Permafrost and Periglacial Processes, 14, 3 19-32 9.
http://dx.doi.org/10.1002/ppp.463
[6] Arcone, S.A., Prentice, M.L. and Delaney, A.J. (2002) Stratigraphic Profiling with Ground Penetrating Radar in Per-
ma fr o st : A Review of Possible Analogs for Mars. Journal of Geophysical Research, 107 , 18-1-18-14.
[7] Daniels, D.J. (2004) Ground Penetrating Radar. 2nd Edition, IEE Radar, Sonar and Navigation Series 15 (Ed.). The In-
stitution of Electrical Engineers, London.
http://dx.doi.org/10.1049/pbra015e
[8] Irvine-F ynn, T.D.L., Moorman, B.J., Williams, J.L.M. and Walter, F.S.A. (2006) Seasonal Changes in Ground-Pene-
trating Radar Signature Observed at a Polythermal Glacier, Bylot Island, Canada. Earth Surface Processes and Land-
forms, 31 , 892-909.
http://dx.doi.org/10.1002/esp.1299
[9] Xiao, J.-P. (2009) Permafrost Research Foundation Detection and Application-Specific GPR . Postdoctoral Research
Report, Changsha, Central South University, 51-52.
[10] Guo, Z.-W. (2010) Application of Predictive Deconvolution in the Special Radar Detection Test of Permafrost Re-
search Data Processing. Master Thesis, Changsha, Central South University, 39-44.
[11] Hansson, K. (1988) Water and Heat Transport in Road Structures, Development of Mechanistic Models. PhD Th es is ,
Uppsala University, ACTA.
[12] Brandt, O. and La n gl e y, K. (2 007) Detection of Buried Ice and Sediment Layers in Permafrost Using Multi-Frequency
Ground Penetrating Radar: A Case Examination on Svalbard. Remote Sensing of Environment. Special Issue: Remote
Sensing of Cryosphere, 111, 212 -227.
http://dx.doi.org/10.1016/j.rse.2007.03.025
[13] Stevens, C.W., Moorman, B., Solomon, S. and Hugenholts, C. (2009) Mapping Subsurface Conditions within the Near-
Shore Zone of an Arctic Delta Using Ground Penetrating Radar. Cold Regions Science and Technology, 56, 30-38.
http://dx.doi.org/10.1016/j.coldregions.2008.09.005
[14] Robinson, E.A. and Treitel, S. (1980) Geophysical Signal Analysis. Prent ice-Hall, Inc.
[15] Yilmaz, Ö. (1987) Seismic Data Processing: SEG.
[16] Leinbach, J. (1995) Wiener Spiking Deconvolution and Minimum-Phase Wavelets: Tutorial. The Leading Edge, 14,
189-192.
http://dx.doi.org/10.1190/1.1437110
[17] Robinson, E.A. (1954) Predictive Decomposition of Time Series with Applications to Seismic Exploration: Ph.D. The-
sis, MIT, Cambridge.

Z. W. Guo et al.
47
[18] Robinson, E.A. (1957 ) Predictive Decomposition of Seismic Traces. Geophysics, 22, 767-778.
http://dx.doi.org/10.1190/1.1438415
[19] Guo, Z.-W., Liu, J.-X., Xi ao, J.-P., Tong, X.-Z., Zhang, W. and Li, J. (2010) GPR Data Processing for Permafrost De-
tection in Qinghai-Tibet Railway. Progress in Electromagnetic Research Symposium, 995-99 8.
[20] Guo, Z.-W., Liu, J.-X., Xiao, J.-P. and Tong, X.-Z. (2010) Detection of Interfaces between Frozen and Melted Sedi-
ment Using GPR: A Case Examination on Qinghai-Tibet Railway. Progress in Electromagnetic Research Symposium,
3, 990-994.