Received 17 March 2015; accepted 10 July 2015; published 17 July 2015

ABSTRACT

A key stage for Kriging interpolation is the estimating of variogram model, which characterizes the spatial behavior of the variables of interest. But most traditional kriging interpolation has finite types of empirical variogram model, and sometimes, the optimal type of variogram model can not be find, which result in decreasing interpolation accuracy. In this paper, we explore the use of Multi-Gene Genetic Programming (MGGP) to automatically find an empirical variogram model that fits on an experimental variogram. Empirical variogram estimation based on MGGP, in contrast with traditional method need not select type of basic variogram model and can directly get both the functional type as well as the coefficients of the optimal variogram. The results of case study show that the proposed method can avoid the subjectivity in choosing the type of variogram models and can adaptively fit variogram according to the real data structure, which improves the interpolation accuracy of kriging significantly.

Keywords:

MGGP, Kriging Interpolation, Variogram

1. Introduction

Mineral grades are generated through the geological processes not always completely known or understood. The description and modeling of spatial correlation allows better understanding of the depositional processes and improves on the prediction of mineralization and mineral grades at non-sampled locations. The modeling of the spatial variability has become a standard tool of mineral resource analysts. Kriging is an interpolation technology which estimates or predicts the spatial phenomenon at non-sampled locations from sparse sample data based on a stochastic model of spatial variation (Chiles & Pierre, 1999) [1]. Comparing with the other interpolation methods, kriging provides not only predictions but also the kriging variances or errors, which makes the best use of existing knowledge by taking account of the way a property varies in space through the variogram function. So it is known as a best linear unbiased predictor that is widely used in the related fields (Oliver, 2010) [2].

The key stage for kriging interpolation is the estimating of empirical variogram model. Its precision ensures that the variogram estimate is sufficiently accurate for kriging interpolation (Zhang, 2005) [3]. The rational empirical variogram model is estimated based on the experimental variogram distribution. The traditional method must choose type of the basic variogram model in advance and then the coefficients of selected model can be estimated using several optimization techniques. However, the known types of basic variogram model is finite and their selection is subjective, and sometimes, the optimal type of empirical variogram model cannot be find, which result in decreasing interpolation accuracy.

This paper aimed to overcome this problem, so we presented the new method based on MGGP for estimation of empirical variogram. The main advantage of proposed method over the traditional method is that it uses the ability of genetic programming to generate mathematical expressions of empirical variogram model without assuming any prior type of the basic variogram model. So, it can avoid the subjectivity in choosing the type of variogram models and can automatically fit variogram according to the real data structure, which improves the kriging interpolation accuracy.

2. General Principle of Kriging Interpolation

Kriging is the geostatistical method of interpolation for random spatial processes. The original formulation of kriging, now known as ordinary kriging, is the most robust method and is the one most often used (Oliver, 2010) [2]. Kriging predicts unknown values from a weighted average of sparse sampled values in the neighborhood of non-sampled location based on a stochastic model of spatial variation. The above-mentioned spatial variation of data on different locations is expressed by the variogram. Details are as follows:

Consider that a random variable, Z, has been measured at sampling locations x_i, i = 1, …, n, and we want to estimate its value at a non-sampled location x₀. Then it is calculated from a weighted linear combination of the measured values:

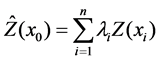. (1)

where n usually represents the data points and l_i are the weights. To ensure that the estimated value is unbiased the weights are made to sum to one.

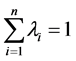(2)

At this time, in order to determine spatial dependence of data on different locations, variogram is introduced. The experimental variogram can be calculated as following:

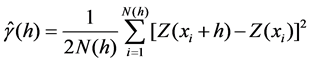(3)

where Z(x_i + h) and Z(x_i) are the actual values of Z at sampled locations x_i + h and x_i, and N(h) is the number of pairs separated by the vector lag distance h.

In general terms, after the experimental variogram is computed by Equation (3), we usually choose a rational empirical variogram model based on the observation of experimental variogram distribution or prior knowledge and then fit experimental variogram to the selected theoretical model. The most commonly used theoretical model of empirical variogram includes spherical model, exponential model and Gaussian model.

・ The spherical model:

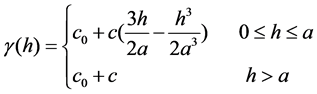(4)

・ The exponential model:

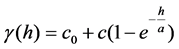(5)

・ The Gauss model:

(6)

Among them, c₀ is the nugget constant, (c₀ + c) is the sill, a is the range. They are unknown coefficient of model that should be finding.

In this stage, the exact quantification of variogram should be affect directly to the accuracy of kriging. So, a number of researchers pay attention to estimation of empirical variogram. At present, the rational variogram model is often identified based on the comparison of different variogram models. However, the types of theoretical variogram models are very finite, the choosing of variogram model deservedly contain some subjectivity, and also sometimes, the obtained empirical variogram could not reflect exactly the spatial variation of real data.

Once empirical variogram is determined, at the next stage, the kriging linear equation is derived by using the estimated empirical variogram:

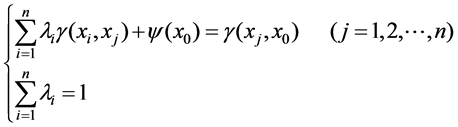(7)

where g(x_i, x_j) is the value of variogram between sampled locations x_i and x_j, g(x_j, x₀) is the value of variogram between sampled locations x_j and non-sampled location x₀, y is the Lagrange multiplier. The Lagrange multiplier y is introduced to achieve minimization. The kriging weights are calculated according to above Equation, and then the prediction of Z at x₀ can be obtained by inserting the weights l_i into Equation (1). The kriging variance is then:

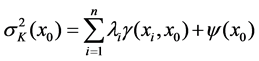(8)

3. MGGP

Genetic Programming (GP) developed by Koza in 1992 [4] is considered to be the most famous for solving symbolic regression problems and is widely used in modeling processes of varying nature. GP based on Darwin’s theory of “survival of the fittest” finds the optimal solution by mimicking the process of evolution in nature (Gandomi & Alavi, 2012; Koza, 1992) [4] [5]. GP generates both of model types and its coefficients automatically based on the given input data. The main advantage of GP over the other regression analysis and statistical modeling techniques is that it has the ability to generate mathematical expressions without assuming any prior form of the existing relationships.

MGGP is a robust variant of GP, which effectively combines the model structure selection ability of standard GP with the parameter estimation power of classical regression by using a new characteristic called multi-gene. In traditional GP method, the model is a single tree/gene expression whereas in MGGP, the model formed is a linear combination of several low order non-linear trees/genes which each of them is a traditional GP tree (Searson, Leahy, & Willis, 2010) [6] [7]. Recently, the MGGP have been used successfully for engineering modeling problems (Gandomi & Alavi, 2012; Garg, Garg, & Tai, 2014) [4] [5]. It has been shown that MGGP regression can be more accurate and efficient than the standard GP for modeling nonlinear problems.

The steps generally followed in MGGP are:

1) Creation of an initial population of individuals.

2) Evaluation of fitness of individuals.

3) Selection of the fittest individuals as parents.

4) Creation of new individuals (also called the offspring) through the genetic operations of crossover, mutation, and reproduction.

5) Replacing the weaker parents in the population by the stronger ones.

6) Repetition of steps 2 through 5 until the user defined termination criterion is satisfied. The termination criterion can be completion of a specified number of generations or fitness criterion such as minimum error reached.

Each individual are composed of the terminal and function set. The function set can be composed of the arithmetic operators (+, -, /, ×), non-linear functions (sin, cos, tan, exp, tanh, log), Boolean operators (and, or, etc.) or the other operators as defined by the user. The elements of the terminal set can be input process variables and random constants.

The key difference between GP and MGGP is that, in the latter, the model participating in the evolution is a combination of several sets of genes/trees. For a system with u input of dimension R^n×m to produce a model output y with dimension R^n×1, where n is the number of observations taken and m is the number of input variables, we could produce a tree structure which introduces the mathematical relationship:

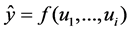(9)

In MGGP symbolic regression, each prediction of the output variable ŷ is formed by a weighted output of each of the trees/genes in the multi-gene individual plus a bias term. Each tree is a function of zero or more of the i input variables u₁, …, u_i. Mathematically, a MGGP model can be written as:

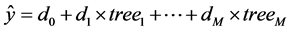(10)

where d₀ represents the bias or offset term while d₁, …, d_M are the gene weights and M is the number of genes (i.e. trees) which constitute the available individual. The weights (i.e. regression coefficients) are automatically determined by a least squares procedure for each multi-gene individual. In multi-gene symbolic regression, each symbolic model is represented by number of GP trees weighted by linear combination. Each tree is considered as a gene by itself. The typical example of MGGP model and its mathematical expression are shown in Figure 1.

4. Kriging Interpolation Using MGGP

Considering the variogram model estimation problem, we proposed the kriging interpolation method combined with MGGP. In this approach, MGGP automatically fit the variogram curve without assuming prior type of basic model, so there is no need to choose the theoretical variogram model and the optimal empirical variogram can be got directly.

The specific steps in kriging interpolation using MGGP are as follows:

・ Calculate the experimental variogram 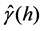using Equation (3);

・ Use MGGP to fit experimental variogram, then get the empirical variogram g(h);

・ Based on the estimated empirical variogram, get the weights l₁, …, l_n for every neighboring point x_i and then obtain the estimated value Z(x₀) and kriging variance 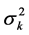(x₀) at x₀ by using Equation (7), Equation (1) and Equation (8);

5. Case Study

This section aimed to compare the proposed method with the traditional method in kriging interpolation. For this illustration, we have selected data of the simulated coal mine taken from a geostatistical study (Clark, Harper, & Ohio, 2000) [8]. The coal mine data used in this study can be accessed from http://www.kriging.com/datasets/. This set of data based on a real coal seam in Southern Africa. It includes 116 borehole samples drilled into a coal seam. Several measurements are made on each sample: width of coal seam (m); calorific value of the coal (KJ); and the vertical location of the top of the seam (elevation, m). Among them, the calorific value of the coal is selected for the predictable variable with kriging interpolation. All coordinates are in meters. The calorific

value of the coal ranges from 17.21 KJ to 26.90 KJ, and the spatial distribution of this variable are shown in Figure 2.

Firstly, calculate the experimental variogram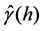. Experimental variogram is calculated at lags h_l = 225 ´ l (meter), l = 1, …, 30 by using Equation (3) based on the known calorific value data.

Secondly, estimate empirical variogram g(h). In this paper, 3 empirical variogram are obtained based on experimental variogram (Figure 3). Excepting MGGP variogram, the other two empirical variogram is fitted by a weighted least-squares algorithm.

In estimating empirical variogram model, the implementation of MGGP method requires adjustment of its parameters.

The parameter selection is important since it affects the generalization ability of the MGGP model. The parameters selected based on trial-and-error approach are shown in Table 1. The parameters like population size and number of generations fairly depends on the complexity of the regression problem. In generally, the population size and number of generations should be fairly small for training data of larger samples. Since a MGGP model is formulated from the set of genes, the model will have higher complexity i.e. greater number of nodes along with the evolution, and may result in over-fitting. The restriction on the maximum number of genes and depth of the gene exerts control over the complexity of the models and results in accurate and compact models. Therefore, in this study, the maximum number of genes and maximum depth of gene is kept at 2 and 3, respectively. The fitness function used for performance evaluation of population in the empirical variogram estimation is root mean square error, given by:

(11)

where G_i is the predicted value at the ith lag distance by the MGGP model, is the experimental variogram value at the ith lag distance and N is the number of training samples. The mathematic expressions of estimated empirical variogram are shown in Table 2.

Then, from the corresponding observed data and estimated variogram models, kriging prediction and kriging variance were computed at unknown point x₀ according to the Equation (7), Equation (1) and Equation (8).

Finally, as a comparison of the kriging interpolation results obtained with different approach, the cross-vali- dation technique was used. That is, we attempt to validate our models by dropping out each observed values and cross estimating the value at that location from the neighboring residual samples. For each spatial location x_i, based on the set of observations without Z(x_i), a predictor of Z(x_i) is calculated as following:

(12)

And their kriging variance is obtained correspondingly.

Then compare it with the real value and makes error statistics analysis. The mean absolute prediction error (MAPE), root mean square prediction error (RMSPE) and dimensionless averaged squared prediction error (DASPE) were used as the cross validation evaluation indices. They are given as following:

(13)

(14)

(15)

where Z(x_i) is the observed value at sampling location x_i, Ẑ(x_i) is the estimated value, (x_i) is the corresponding kriging variance and N is the number of points for cross-examination. MAPE can express the estimation accuracy generally, and RMSPE is the fundamental measurement comparing the accuracy of different interpolation methods. RMSE is smaller, the interpolation method is better. Error statistics combined with kriging variance is known as a useful statistic for validation of kriging (Casal & Fernández, 2014; Lark, 2000) [9] [10]. If a correct variogram has been used, the kriging variances will be similar to the observed variances, and also DASPE should be close to 1. The results of error statistics analysis are shown in Table 3.

From Table 3, we can see that MAPE, RMSPE of MGGP model are smaller than others and its DASPE is closer to 1. It indicates that MGGP model not only is more exactly fitted to experimental variogram but also has better kriging interpolation performance than other models.

6. Conclusion

The estimating of empirical variogram model is the key stage for kriging interpolation because it becomes the mouthpiece of spatial variation in real field and its exact estimation can affect interpolation accuracy. The results of case study show that the MGGP-based estimation of empirical variogram model has ability that can fits more exactly experimental variogram without assuming basic model type and reflects more objectively spatial variation of real field comparing with traditional method, and that it improves the kriging interpolation precision significantly. So, its application has potential value in deposit prediction.

Acknowledgements

We thank the financial support by Research of High-grade Iron Ore Formation Mechanism and Prediction of China (2012CB416800) and Fundamental Research Funds for the Graduate Innovation State Education Ministry (N110601002).

Cite this paper

Changik Han,Ende Wang,Jianming Xia,Sunggi Yun, (2015) Application of Multi-Gene Genetic Programming in Kriging Interpolation. Journal of Geoscience and Environment Protection,03,27-34. doi: 10.4236/gep.2015.35004

References

NOTES

^*Corresponding author.