Journal of Geoscience and Environment Protection
Vol.03 No.05(2015), Article ID:58066,13 pages
10.4236/gep.2015.35003
Temperature-Dependent Newtonian Rheology in Advection-Convection Geodynamical Model for Plate Spreading in Eastern Volcanic Zone, Iceland
Md. Tariqul Islam, Erik Sturkell
Department of Earth Sciences, University of Gothenburg, Gothenburg, Sweden
Email: tariqul.islam@gvc.gu.se


Received 20 March 2015; accepted 10 July 2015; published 17 July 2015

ABSTRACT
Geodynamic process as advection-convection of the Mid-Atlantic Ocean Ridge (MAR), that is exposed on land in Iceland is investigated. Advection is considered for the plate spreading velocity. Geodetic GPS data during 2000-2010 is used to estimate plate spreading velocity along a profile in the Eastern Volcanic Zone (EVZ), Iceland striking N102˚E, approximately parallel to the NUVEL-1A spreading direction between the Eurasian and North American plates. To predict subsurface mass flow patterns, temperature-dependent Newtonian rheology is considered in the finite-element models (FEM). All models are considered 2-D with steady-state, incompressible rheology whose viscosity depends on the subsurface temperature distribution. The thickness of lithosphere along the profile in the EVZ is identified by 700˚C isotherm and 1022 Pa s iso-viscosity, those reach 50 ± 3 km depth at distance of 100 km from rift axis. Geodetic observation and model prediction results show the ~90% of spreading is accommodated within ~45 km of the rift axis in each direction. Model predicts ~8.5 mm∙yr−1 subsidence at the surface of rift center when magmatic plumbing is inactive. The rift center (the highest magmatic influx is ~11 mm∙yr−1) in model shifts ~10 - 20 km west to generate observed style surface deformation. The spreading velocity, isotherm and depth of isotherm are the driving forces resulting in the surface deformation. These three parameters have more or less equal weight. However, as the center of deformation in the EVZ shifts and most of the subsidence takes place in the volcanic system that is currently the active which is the located of plate axis.
Keywords:
Mid-Atlantic Ocean Ridge, Advection-Convection, Plate Spreading, Geodynamic Modeling, Newtonian Rheology

1. Introduction
The only sub-aerial manifestation of the Mid-Atlantic Ocean Ridge (MAR) is located on Iceland and is defined by epicentres of Earthquake (Einarsson, 2008) [1] and the zone of active volcanism (Figure 1). The plate
Figure 1. The plate boundary in Iceland. The neovolcanic zone Iceland is divided into Northern (NVZ), Eastern (EVZ) and Western Volcanic Zones (WVZ). Black lines represent the approximate central axis of divergent plate boundary segments and the dashed lines indicate offset by two transform fault systems i.e. South Iceland Seismic Zone (SISZ) in the south and Tjörnes Fracture Zone (TFZ) in the north. Ellipses locate the central volcano. Fissure swarms (dark grey) and major glacier (white) are outlined. Black vectors present full spreading relative to stable Eurasian plate according to NUVEL-1A (DeMets et al., 2010). AKUR, HOFN and REYK (black circles) are geodetic continuous GPS stations. Eurasian plate (EuP), Hreppar block (HB), Kolbeinsey ridge (KR), North American plate (NAP), Reykjanes ridge (RR) and Vatnajökull (VT) are also shown. Grey rectangle indicates the region of Figure 2(A), profile locations in EVZ.
boundary across Iceland is slow spreading rate (~2 cm∙yr−1). The ridge segments across Iceland are characterised by central volcanos with associated fissure swarms. The volcanic systems have been grouped into the Western (WVZ), Eastern (EVZ) and Northern Volcanic Zones (NVZ) (Figure 1).
The plate spreading style in Iceland has been fitted using an elastic dislocation model by several authors (e.g., LaFemina et al., 2005; Árnadóttir et al., 2006, 2009; Scheiber-Enslin et al., 2011; Geirsson et al., 2012), [2]-[6] a stretching model (e.g., Pedersen et al., 2009) [7] and a temperature-dependent, non-linear rheology model (Islam et al., 2013) [8]. The applied rheology is elastic in the elastic half-space in a dislocation model and a uniform elastic-viscoelastic half-space in stretching model where strain rate is linear to stress. All models are constrained to fit the observed surface deformation. However, the pattern of subsurface flow and the rheology beneath Iceland can be predicted by advection-convection modeling. It may provide new insights into a nature of plate tectonic motion in MAR system. Here we investigate advection-convection geodynamical models using temperature-dependent Newtonian rheology for plate spreading as measured by Global Positioning System (GPS) in EVZ, Iceland.
1.1. Geological Settings
Iceland is mainly made of basalt which corresponds to ~92% surface area of postglacial volcanic zone. Remains are basaltic andesites (~4%), andesites (~1%) and dacite-rhyolites (~3%) (Jakobsson, 1979) [9]. Half of Iceland is covered by tertiary rock of older than 3.3 myr. The age of oldest rock is ~14 - 15 myr and found in the western and eastern Iceland (Sæmundsson, 1986) [10]. The geology around the plate boundary in the EVZ is dominated by Postglacial lava fields (<11 kyr), Upper Pleistocene (<0.8 myr) and Pilo-Pleistocene (0.8 - 3.3 myr) (Jóhannesson & Sæmundsson, 1998) [11].
In Iceland numerous of refraction seismic studies have been performed in order to determine the thickness of its crust and the location of Moho (e.g., Darbyshire et al., 2000; Kaban et al., 2002; Brandsóttir & Menke, 2008; Bjarnasson & Schemeling, 2009) [12]-[15]. The crustal thickness under Iceland decreases from central Iceland to coastal areas. Crustal thickness varies from ~19 km in the west central Iceland to 32 km in the east and east central part (Bjarnason & Schemeling, 2009) [15]. The thick-crust and thin-crust models assume to ~40 km relatively cool and ~10 - 15 km hot thicken crust, respectively (Flóvenz & Sæmundsson, 1993; Björnsson, 2008) [16] [17]. However, the demarcation line between crust and upper mantle, the Moho, that is suggested lie at depth of ~20 km under an active central volcano (e.g., Krafla area) to ~29 km at the central Iceland (Durbyshire et al., 2000) [18].
1.2. Tectonic and Volcanic Settings
The plate-spreading rate in Iceland varies from 18.8 - 18.3 mm∙yr−1 (Figure 1) in the direction to N102.7˚E- N105.3˚E depending on latitude that is predicted by the NUVEL-1A model (DeMets et al., 2010) [19]. The geodetic measurement shows that the plate spreading in the EVZ decreases from north towards south (LaFemina et al., 2005; Scheiber-Enslin et al., 2011) [2] [5]. The measured full spreading rate (100%) is estimated just south of Vatnajökull that corresponds to 19.8 mm∙yr−1 (LaFemina et al., 2005; Scheiber-Enslin et al., 2011) [2] [5]. Towards the south-east, south of Torfajökull (Figure 2), the spreading rate is estimated to 45% by the full rate that is 9 mm∙yr−1 (Scheiber-Enslin et al., 2011) [5].
Figure 2. Displacements of GPS sites and location of tilt stations in the EVZ. (A) The location of GPS sites are presented by black triangles and located on different fissure swarms, e.g., Torllagígar (T), Eldgja (E) and Lakegígar (L). The black rectangles (DOMA and NORD) locate the tilt stations. The dashed line indicates a profile striking N102˚E that is approximately parallel to the spreading direction (NUVEL-1A). Arrows show horizontal velocities with 1σ uncertainties of GPS sites, relative to stable North American plate in ITRF2005 reference frame. (B) Horizontal velocities projected onto strike N102˚E versus station distance along the profile show in (A). Error bars represent 1σ uncertainties for the longitudinal component. The curve gives the best fitting. DZ indicates deformation zone of ~90 km width contains ~90% deformation. (C) Vertical surface velocities during 2000-2010 along the profile, relative to the ITRF2005 reference frame.
The EVZ has been activated for ~2 - 3 mm∙yr, after a rift shifts towards its present location, during the most recent ridge jump towards east from the WVZ (Sæmundsson, 1974) [20]. It is propagated ~35 - 50 mm∙yr−1 towards south east (Einarsson, 1991) [21]. The EVZ and WVZ are separated in the northern, in the east-west direction by the Hreppar block (HB), a micro plate and in the south they are connected by South Iceland Seismic Zone (SISZ), a fault zone (Figure 1). The crustal deformation caused by spreading is associated with central volcanos, to their fissure swarms and the geometry of volcanic systems. The geometry in the EVZ is the parallel (Figure 1 and Figure 2) and not in an-echelon pattern as in the NVZ (Figure 1). The dominant fissure swarms in EVZ are directed to ~N45˚E those are ~30˚ oblique to the direction of NUVEL-1A predicted plate motion (LaFemina et al., 2005) [2].
Historical five rifting episodes, e.g., Vatnaoldur, Eldgja, Veidivötn, Lakegígar and Trollagígar are documented (Jónsson et al., 1997; Venzke et al., 2002) [22] [23]. The Lakegígar (1783-1784) and the Trollagígar (1862-1864) (Figure 2(A)) has the most recent rifting episodes (Jónsson, 1997) [22]. The Lakegígar produced ~16 km3 erupted product (~4.5 m thick and ~70 km long dike) whereas the Trollagígar produced ~0.3 km3 product (~1.5 m thick and ~45 km long dike).
1.3. Thermal Structure
Temperature gradient in the crust beneath Iceland varies widely from almost 0˚C∙km−1 to 500˚C∙km−1 (Flóvenz & Sæmundsson, 1993) [16]. In the flank zones of active volcanic zones, it is ~150˚C∙km−1 - 200˚C∙km−1. However, in the oldest rock locates away remotely from the active volcanic zones, temperature gradient ranges from ~40˚C∙km−1 - 50˚C∙km−1 (Flóvenz & Sæmundsson, 1993) [16]. It is assumed in the center of the rift zone a thin-crust model with 10 - 15 km depth and with a partially molten (10% - 15%) basaltic rock gives a temperature of ~1100˚C. The thick-crust model gives temperature ~600˚C - 800˚C beneath curst (~20 - 40 km) (Flóvenz & Sæmundsson, 1993; Björnsson, 2008) [16] [17]. Kaban et al. (2002) [13] suggest that at the depth of ~30 - 50 km, the temperature is ~1200˚C, which reaches at a ~20 km depth beneath active volcanic zone in NVZ. Most of the authors present temperature of ~950˚C in the Moho and ~600˚C at ~7.0 - 7.2 km depth of the elastic crust in the rift zone.
1.4. Previous Study of Spreading in EVZ
Geodetic GPS studies of crustal deformation for plate spreading have been conducted in several major campaigns (LaFemina et al., 2005; Árnadóttir et al., 2006, 2009; Scheiber-Enslin et al., 2011; Geirsson et al., 2012) [2]-[6]. The observed crustal deformation across the plate boundaries has been used in models with opening dyke, with the locking depth as an important parameter. In this model, a normal dike moves horizontally along the spreading axis under a locking depth. The locking depth is treated loosely to the depth of elastic crust (LaFemina et al., 2005) [2]. Okada (1985) [24] formulas have been applied often to calculate corresponding surface deformation. An elastic half-space is used as rheology to constrain the models. Further, LaFemina et al. (2005) [2] added a visco-elastic half-space with a uniform viscosity beneath a uniform elastic layer to investigate rifting cycle effects. The results of these studies presented in Table 1. Consideration of pure elastic rheology in models is over simplification of Earth rheology. However Pedersen et al. (2009) [7] suggested that a strong variation of Earth rheology exists in Iceland based on surface and ridge axis. All of these models reveal the shortcoming of the continuous variation of rheology in both horizontally and vertically.
An advance model of temperature-dependent non-linear rheological model is constrained by Islam et al. (2013) [8]. In this model, rheology varies considering both depth and horizontal distance from a ridge axis. This variation is temperature dependent. But this model does not allow convection at the depth of the asthenosphere. In addition, a hot upper mantle is upwelling beneath the Iceland (Sigmundsson, 2006) [25]. With this knowledge the next step in the modeling of the rift zone, is a model which allow convection in depth of the asthenosphere using a temperature-dependent rheology. This is what the study attempts.
2. Geodetic Data and Velocity
2.1. Geodetic GPS Data
Geodetic GPS data for EVZ is originated from Geirsson et al. (2012) [6], and it spanns the period 2000-2010 (Table 2). The measurements were calculated in the International Terrestrial Reference Frame 2005 (ITRF2005)
Table 1. Estimated spreading rate and locking depth extracted from literatures.
Table 2. Site location and displacement velocity in ITRF2005 and relative to stable North American plate during 2000-2010. Velocity relative to stable North American plate are corrected for 2008 Earthquake Offsets and glacial isostatic rebound. Data are obtained from Geirsson et al. (2012) [6].
(Altamimi et al., 2007) [26]. Further the horizontal velocity was calculated relative to stable North American plate. This data set was corrected for offets caused during a 2008 earthquake and glacioisostatic adjustment (GIA) by Geirsson et al. (2012) [6]. The horizontal velocities are projected on to a profile in direction N102˚E, which is the predicted plate spreading direction according to the NUVEL-1A model. This profile is located between north of Torfajökull and south of Vatnajökull, reaching into Hreppar block (Figure 2(A)), in the way similar to the second profile of LaFemina et al. (2005) [2].
The spreading velocity (V) along the profile is calculated by modification of Savage & Burford (1973) [27] to fit observed displacement as following as in
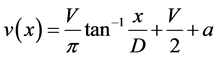 (1)
(1)
where x is horizontal distance perpendicular to rift axis, D (same unit as for x) defines the width of arctangent curve, α is used as offset if two or more parallel zones exist. The α ≡ 0 when V is calculated for a single independent spreading zone, e.g., NVZ in Iceland. When V is shared by two or more adjacent interdependent spreading zones e.g., WVZ and EVZ, α = 0 to calculate V for first zone. The α = maximum of site velocity in the first zone or minimum of second zone, the contribution of first zone where the first zone terminates extension and it is transferred to the adjacent second zone and so on. The V is calculated by minimizing the root-mean-square error (RMS error) between observed site velocity and fitting curve v(x). Unite of V is same as for observation site velocity and here it is mm∙yr−1.
Along the profile crossing the EVZ, the spreading rate is estimated to V = 14 ± 2 mm∙yr−1 by applying Equation (1) where D = 14.7 km and α = 2.87 mm∙yr−1. The best fitting curve, v(x) gives RMS error = 0.88 mm∙yr−1 (Figure 2(B)). This velocity is similar with that suggested by LaFemina et al. (2005) [2] (14.6 ± 1.3 mm∙yr−1) and Scheiber-Enslin et al. (2011) [5] (12.5 - 15.3 mm∙yr−1).
2.2. Tilt Data
Five optical levelling lines have been installed and measured in and around the Torfajökull volcano. One of these is situated in the caldera and has indication ground motion implied to a magma chamber (Scheiber-Enslin et al., 2011) [5]. The DOMA station north of the caldera at Dómadalshraun (Figure 2(A)) and seems to be unaffected of the magma chamber induced motion >10 km away and the ground deformation is likely attributed to active in the rift zone.
The tilt vectors (showed as upward tilt) are oriented in the plate spreading direction, perpendicular to the strike of the volcanic system (or plate boundary). The tilt vector shows upward tilt in opposite directions over time. During the whole span (1994-2006) of the tilt measurements the center of subsidence has been to its east (Scheiber-Enslin et al., 2011) [5]. As the EVZ compare of the five parallel volcanic systems (Figure 2(A)), the center of plate boundary spreading can only be located in on system at the time, which center of subside in the current active one. The upward tilt vector will point away from the center of the spreading. During 2001-2006, the Dómadalshraun shows several shifts to 180˚ in direction of the upward till vector, point away and alternates forwards the center of spreading (in Scheiber-Enslin et al., 2011) [5]. Slip on a normal fault plane gives a local deformation field. A good example of this is for Thinvellir graben in the WVZ that the levelling line stretches to the plate boundary and in the early 1970s experience a 40 m slip on one of its boundary faults to the west of the center of subsidence (Gudmundsson, 1987) [28]. This causes a 180˚ shift in the tilt vector. The most likely explanation for this is slops on normal faults near the tilt station. An example of the local deformation field at a normal fault can case a tilt vector (upward) to point toward the center of the spreading.
3. Geodynamic Modeling
Our geodynamic modeling is based on a cooling the oceanic lithosphere. To explore subsurface temperature distribution and mass-flow pattern, COMSOL Multiphysics 4.3b finite-element software package is used. The simulation for subsurface mass-flow is conducted by coupling of a thermal structure and the flow of rheology. All implemented models are two dimensional (2D). The domain of these models is 100 km in depth and 200 km length crossing the rift axis in perpendicular direction of both sides (Figure 3). The plate spreading is applied as advection. All models are executed using temperature dependent Newtonian rheology which is further compared with a uniform viscosity of 1 × 1019 Pa∙s.
The viscosity of Newtonian rheology is dependent on temperature. Temperature dependent viscosity is calculated by
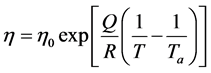 (2)
(2)
Figure 3. Thermal and fluid flow boundary conditions. (A) At the surface and beneath 30 km at the ridge axis, T is fixed to 278 and 1573 K, respectively. At 12 and 20 km depth of the ridge, T is 973 and 1273 K. Intermediate space at the ridge axis, T increases linearly. (B) Above the isotherm 973 K, both left and right vertical boundaries are allowed to outflow as plate spreading. Influx through the bottom horizontal boundary is allowed with no stress as Model A (Table 3). The observed surface deformation is not applied.
where η0 is the reference viscosity of 1 × 1018 Pa∙s, Q is the activation energy of 250 kJ∙mole−1, R is the gas constant, Ta is the temperature of ridge axis in asthenosphere and T is the subsurface temperature, both in K (Behn et al., 2007) [29]. This gives a linear approximation of non-linear rheology (Christensen, 1983) [30]. The reference viscosity is obtained from Pagli et al. (2007) [31] and, Jones & Maclennan (2005) [32], who suggest the viscosity of rheology beneath Iceland is order of 1018 Pa s. The Equation (2) gives viscosity higher than 1022 Pa s in temperature less than 700˚C. Any viscosity higher than 1022 Pa∙s is fixed to 1022 Pa∙s.
Model Implementation
First, we calculated a steady-state temperature distribution in the solid subsurface using the thermal structure suggested by Durbyshire et al. (2000) [18], Kaban et al. (2002) [13] and Björnsson (2008) [17] who from seismogenic studies in Iceland. The temperature is used as a boundary condition for the thermal model which is applied at the surface and the ridge axis (Figure 3(A)). A constant temperature 1300˚C is set in the interval 30 - 100 km depth, is used for the asthenosphere (Turcotte & Schubert, 2002) [33]. The temperature distribution in solid materials is controlled by the basic energy-balance equation as (COMSOL Multiphysics, 2013) [34],
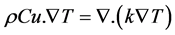 (3)
(3)
where ρ is the material density, C is the heat capacity at constant pressure of 1000 J∙kg−1∙K−1, u is the advection velocity, T is the temperature and k is the thermal conductivity = 1.9 W∙m−1∙K−1. Average density of lithosphere- asthenosphere is set to 3300 kg∙m−3 (e.g., Behn et al., 2007; Roland et al., 2010) [29] [35]. The temperature distribution in the model is presented in Figure 4(A).
We use the 700˚C (973 K) isotherm from Turcotte & Schubert (2002) [33] to demarcate the boundary between the lithosphere and asthenosphere, for hot and dry rheology. Since the rheology of newly formed upwelling Earth crust beneath Iceland is very hot and dry (Barnhoorn et al., 2011) [36]. Therefore, above the 700˚C isotherm, the left and right vertical boundaries of the models are allowed for advection at a rate of 7 mm∙yr−1, which corresponds to the total spreading rate of 14 mm∙yr−1 (Figure 3(B)). Temperature 700˚C isotherm at 12 km depth is used for boundary condition since as the 12 km elastic depth is found by elastic dislocation modes (e.g., LaFemina et al., 2005; Geirsson et al., 2012) [2] [6], and a similar depth is obtained by the 700˚C isotherm applying a temperature-dependent, non-linear rheological model along the same profile (Islam et al., 2013) [8].
Based on convection at the bottom boundary with no stress and, the observed vertical uplift and subsidence along the profile, eight different models are evaluated (Table 3).
Figure 4. Sub-surface temperature distribution and viscosity along profile in the EVZ, Iceland. Depth (km) ridge is in y axis. (A) The line indicates isotherm of 973 K (700˚C) which defines the depth of lithosphere allow for advection. (B) Viscosity Pa s in Log 10 base. Viscosity above 1022 Pa s belongs to lithosphere that behaves in brittle state.
Table 3. Fluid flow boundary conditions. Advection as plate spreading is applied to all models.
aTemperature dependent Newtonian rheology. bUniform rheology viscosity to 1 × 1019 Pa∙s.
Then, Laminar flow is executed in incompressible flow mode, which is governed by mass balance equation as
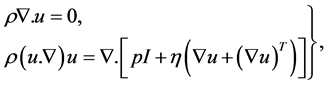 (4)
(4)
where ρ is the material density, η is the dynamic viscosity, u is the velocity and p is the pressure (COMSOL Multiphysics, 2013) [34]. The numerical solution follows minimization of residual of Newton method and weighted Euclidean norm for a convergence criterion. A tolerance of 1 × 10−6 is allowed to estimate relative error. A priori and posterioei error is generated by numarical solution which depends to element size. This error tends to null when element size tends to zero (Larson & Bengzon, 2009, p-27-28, 39-41) [37]. Therefore extremly fine elements (Physics-controlled mesh) in ranging 2 - 670 m (triangular), with 1.05 maximum growth rate, 0.2 resolution of curvature and 1 resolution of narrow regions are applied to minimize priori and posterioeri error.
4. Results and Discussions
The width of deformation zone in EVZ along the profile is estimated to be ~90 km based on where the slope’s gradient of the fitting curve (v(x)) is equal to zero or close to zero. More than 90% surface deformation occurs within this zone (Figure 2(B)).
The hypothesis of geodynamic modeling in this study is lithosphere is floating on top of asthenosphere in the MAR system (Turcotte & Schubert, 2002; Fowler, 2005) [33] [38]. The temperature structure in Figure 4(A) is the most likely subsurface thermal structure along the profile in EVZ, Iceland. The thermal distribution is similar as to the Pálmason model to describe the Icelandic crustal accretion model (Pálmason, 1986) [39].
The viscosity in the temperature dependent Newtonian rehological models was not allowd to exceed 1022 Pa∙s in the region at lower temperature (<700˚C), that is in shallow depth (Figure 4). Since empirical experiment of olivine (Turcotte & Schubert, 2002) [33] shows that maximum viscosity at low temperature is ~1022 Pa∙s. Therefore a temperature depenent rheology (Figure 4(B)) is obtained by Equation (2) that gives the best agrement with the viscosity of olivine experiment (Turcotte & Schubert, 2002) [33] and the 1022 Pa∙s iso- viscosity for ductile-brittle transition for the dry rheology (Barnhoorn et al., 2011) [36]. The viscosity in low temperature (<700˚C) behaves as in a brittle state, this is a representative of the lithosphere. The 700˚C isotherm and 1022 Pa s iso-viscosity provide a brittle region. They provide lithospheric thickness of 50 ± 3 km (depth) at a distance 100 km from active rift axis (Figure 4), this is in the same scale as the results of Bjarnason & Schmeling (2009) [15].
The sub-surface mass-flow shows distinct pattern when uniform viscosity and temperature dependent vis- cosity are applied (Figure 5). Model A, temperature dependent rheological model is stress free and convection is allowed from bottom, which results ~8.5 mm∙yr−1 subsidence at the rift center and ~10.5 mm∙yr−1 influx (uplift) at the 100 km bottom of ridge center (Figure 5(A)).
Figure 5. Subsurface mass flow pattern in the models. Depth (km) ridge is presented in y axis. The flow pattern is obtained by applying temperature dependent viscosity and uniform viscosity to 1 × 1019 Pa∙s. Subsurface mass flow in A-H is obtained by different rheological properties and boundary conditions as describe in Table 3, accordingly.
Model A may explore the scenario of the crustal deformation in the NVZ where a narrow graben is obsered at rift center (Pederssen et al., 2009) [7]. Model B, uniform rheological (viscosity of 1 × 1019 Pa∙s) model is also stress free and causes an ~8.5 mm∙yr−1 uplifting at the rift center and ~12 mm∙yr−1 magmatic influx at the ridge center of 100 km depth (Figure 5(B)). This phenomenon might be similar as so called central uplift of Iceland. High upwelling activities cause uplifting of whole Iceland (Sigmundsson, 2006; Árnadóttir et al., 2009) [4] [40].
Model C is similar as Model A but convection is not allowed, in model this results to ~9.5 mm∙yr−1 subsidence at the rift center (Figure 5(C)). This model may give the scenario of Thingvellir graben, in the WVZ where magmatic plumbing is almost absent and continuous subsidence is observed from the whole Holocene (Sturkell et al., 2013) [41]. Model D is similar as model B but convection at the bottom is not allowed. It gives ~4 mm∙yr−1 subsidence at the rift center (Figure 5(D)). However at ~60 km depth, mass-flow is not observed. But underplating drives away the plate from the ridge axis where the space is filled up by instrution (Björnsson, 2008) [17]. Therefore this model contradics with flow patter of Pálmason model.
Models E-H are produced by applying observed surface deformation as boundary condition (Figures 5(E)-(H)). Models E and G is temperature dependent, and F and H is uniform rheological model (Table 3). Model E gives ~11 mm∙yr−1 magmatic influx ~10 km west of the ridge center in 100 km depth. It also results ~8 mm∙yr−1 magmatic flow towards center of Earth as spriral sink (Hirsch et al., 2004, p 47) [42] ~80 km east of ridge center at 100 km depth (Figure 5(E)). This is due to convection as spiral source (Hirsch et al., 2004, p 47) [42] which further flows toward surface. However, Model F results in a ~5 mm∙yr−1 magmatic influx ~55 km west of rift axis but there is no mass flow observed beneath lithosphere at the east of ridge center (Figure 5(F)). Subsurface mass flow in Model G approaching from east of ridge center towards west (Figure 5(G)). This phenomena is not valid since masses flow with high rate alonge and near at ridge axis according to what in Pálmason model. Model H is simmilar as Model D.
Model E give the best scenario of the EVZ. In the model, ridge axis (high convection rate) is shifted ~10 - 20 km towards west (Figure 5(E)) that is very similar with the vertical component of observation (Figure 2(C)). The tilt measuremnts also give the indication of shifting center.
The subsurface mass flow in a state when observed surface deformation is not applied as boundary condition, gives that more than 90% vertical subsidence are predicted from model within ~45 km from the rift axis (Figure 5(A)). Similarly the horizontal component of masses flow is fairly constant beoynd ~45 km from the rift. This may indicate a deformation zone of ~45 km from the rift axis in each direction, which is fairly similar with the deformation zone observed by the fitting curve of GPS observations (Figure 2(B)). Since convection in the model is allowed from the depth with no stress, mass flows as spiral source in asthenosphere (Figure 5(A)) which refill the empty space caused by advection (plate spreading).
Plate spreading in Iceland is symmetric and thus deformation field is expected to be more or less symmetrical. For example, it is observed in the Thingvellir graben in the WVZ both in the horizontal and vertical deformation (Sturkell et al., 2013) [41]. Deformation (spreading axis) in the EVZ shifts between the five parallel volcanic systems and the systems which currently centared host experience the maximum subsidence (LaFemina et al., 2005) [2]. Therefore, vertical deformation and center of spreading along the profile at the EVZ is “Ping Pong” between the five parallel volcanic systems which seem to be active in turns. When the measured displacement vector (vertical component) is applied as boundary conditions in modeling, this ping pong is predicted and the ridge center is shifted (Figure 5(E)).
High upwelling is associated centrally beneath Iceland, therefore the whole of Iceland is uplifting (Árnadóttir et al., 2009) [4], which may cause uplift at western part across the EVZ. On the other hand, the upper crust at the eastern part of the profile may be loosely connected due to several faults (Figure 2(A)). This may hinder the sharing of the strain of central uplift of Iceland.
5. Conclusions
Here we have introduced geodynamic models of advection-convection in a plate spreading environment. In the models,
・ Newtonian rheology is dependent on the subsurface temperature distribution,
・ the viscosity of Newtonian rheology beneath Iceland varies both vertically and horizontally,
・ the depth of lithosphere in the EVZ along the profile is identified to reach 50 ± 3 km at distance of 100 km from rift axis,
・ at ~45 km from the rift axis ~90% of the spreading is accommodated,
・ ~8.5 mm∙yr−1 subsidence at the surface of rift center is predicted when magmatic plumbing is inactive and
・ predicted rift center is shifted ~10 - 20 km west to generate observed style surface deformation and in such case the highest magmatic influx is ~11 mm∙yr−1.
This deformation zone in model depends to spreading velocity, isotherm and depth of isotherm. However, all these three parameters have more or less equal weight. This type of model is comparatively easy to construct based on subsurface temperature distribution which introduce variation of viscosity.
Acknowledgements
Geodetic GPS data for this study was taken from Geirsson et al. (2012). Geirsson, H. and his all co-authors are gratefully acknowledged. The authors thank to Halldór Ólafsson and all others for levelling and geodetic GPS field measurement. Mark Johnson is acknowledged for his valuable comments. Financial support is obtained from Herbert och Karin Jacobssons Stiftelse 11/v15 for publication. We thank NORDVULK for cooperation. The anonymous reviewers are also gratefully acknowledged.
Cite this paper
Md. Tariqul Islam,Erik Sturkell, (2015) Temperature-Dependent Newtonian Rheology in Advection-Convection Geodynamical Model for Plate Spreading in Eastern Volcanic Zone, Iceland. Journal of Geoscience and Environment Protection,03,14-26. doi: 10.4236/gep.2015.35003
References
- 1. Einarsson, P. (2008) Plate Boundaries, Rifts and Transforms in Iceland. Jokull, 58, 35-58.
- 2. LaFemina, P.C., Dixon, T.H., Malservisi, R., árnadóttir, T., Sturkell, E., Sigmundsson, F. and Einarsson, P. (2005) Geodetic GPS Measurements in South Iceland: Strain Accumulation and Partitioning in a Propagating Ridge System. Journal of Geophysical Research, 110, 1-21. http://dx.doi.org/10.1029/2005JB003675
- 3. árnadóttir, T., Jiang, W., Feigl, K.L., Geirsson, H. and Sturkell, E. (2006) Kenematic Models of Plate Boundary Deformation in Sourthwest Iceland Derived from GPS Observation. Journal of Geophysical Research, 111, 1-16. http://dx.doi.org/10.1029/2005JB003907
- 4. árnadóttir, T., Lund, B., Jiang, W., Geirsson, H., Bjornsson, H., Einarsson, P. and Sigurdsson, T. (2009) Glacial Rebound and Plate Spreading: Results from the First Countrywide GPS Observations in Iceland. Geophysical Journal International, 177, 691-716. http://dx.doi.org/10.1111/j.1365-246X.2008.04059.x
- 5. Scheiber-Enslin, S.E., LaFemina, P.C., Sturkell, E., Hooper, A.J. and Webb, S.J. (2011) Geodetic Investigation of Plate Spreading along a Propagating Ridge: The Eastern Volcanic Zone, Iceland. Geophysical Journal International, 1-20. http://dx.doi.org/10.1111/j.1365-246x.2011.05243.x
- 6. Geirsson, H., LaFemina, P., árnadóttir, T., Sturkell, E., Sigmundsson, F., Travis, M., et al. (2012) Volcano Deformation at Active Plate Boundaries: Deep Magma Accumulation at Hekla Volcano and Plate Boundary Deformation in South Iceland. Journal of Geophysical Research, 117, 1-18. http://dx.doi.org/10.1029/2012JB009400
- 7. Pedersen, R., Sigmundsson, F. and Masterlark, T. (2009) Rheologic Controls on Inter-Rifting Deformation of the Northern Volcanic Zone, Iceland. Earth and Planetary Science Letters, 281, 14-26. http://dx.doi.org/10.1016/j.epsl.2009.02.003
- 8. Islam, M.T., Sturkell, E., Sigmundsson, F. and ófeigsson, B.G. (2013) Temperature-Dependent Non-Linear Rheological Models of Plate Spreading in Iceland [abs]. EGU General Assembly, 15, EGU2013-11236.
- 9. Jakobsson, S.P. (1979) Outline of the Petrology of Iceland. Jokull, 29, 57-73.
- 10. Sæmundsson, K. (1986) Suberial Volcanism in the Western North Atlantic. In: Vogt, P.R. and Tucholke, B.E., Eds., The Geology of North America: The Western North Atlantic Region, Geological Society of America, Boulder, 69-86.
- 11. Jóhannesson, H. and Somundsson, K. (1998) Geological Map of Iceland, 1:500000. Bedrock Geology. 2nd Edition, Icelandic Institute of Natural History, Reykjavik.
- 12. Darbyshire, F.A., Priestley, K.F., White, R.S., Stefánsson, R., Gudmundsson, G.B. and Jakobsdóttir, S.S. (2000) Crustal Structure of Central and Northern Iceland from Analysis of Teleseismic Receiver Functions. Geophysical Journal International, 143, 163-184. http://dx.doi.org/10.1046/j.1365-246x.2000.00224.x
- 13. Kaban, M.K., Flóvenz, ó. and Pálmason, G. (2002) Nature of the Crust-Mantle Transition Zone and the Thermal State of the Upper Mantle Beneath Iceland from Gravity Model-ling. Geophysical Journal International, 149, 281-299. http://dx.doi.org/10.1046/j.1365-246X.2002.01622.x
- 14. Brandsdóttir, B. and Menke, W.H. (2008) The Seismic Structure of Iceland. Jökull, 58, 17-34.
- 15. Bjarnason, I.T. and Schmeling, H. (2009) The Lithosphere and Astheo-nosphere of the Iceland Hotspot from Surface Waves. Geophysical Journal International, 178, 394-418. http://dx.doi.org/10.1111/j.1365-246X.2009.04155.x
- 16. Flóvenz, ó.G. and Somundsson, K. (1993) Heat Flow and Geothermal Processes in Iceland and Surrounding Area. Tectonophysics, 189, 1-17. http://dx.doi.org/10.1016/0040-1951(91)90483-9
- 17. Björnsson, A. (2008) Temperature of the Icelandic Crust: Inferred from Electical Conductivity, Temperature Gradient, and Maximum Depth of Earthquakes. Tectonophyscs, 447, 136-141. http://dx.doi.org/10.1016/j.tecto.2006.02.027
- 18. Durbyshire, et al. (2000)
- 19. DeMets, C., Gor-don, R. and Argus, D. (2010) Geologically Current Plate Motions. Geophysical Journal International, 181, 1-80. http://dx.doi.org/10.1111/j.1365-246X.2009.04491.x
- 20. Sæmundsson, K. (1974) Evolution of the Axial Rifting Zone in Northern Iceland and the Tjornes Fracture Zone. Bulletin of the Geological Society of America, 85, 495-504. http://dx.doi.org/10.1130/0016-7606(1974)85<495:EOTARZ>2.0.CO;2
- 21. Einarsson, P. (1991) Earthquakes and Present-Day Tectonism in Iceland. Tectonophysics, 189, 261-279. http://dx.doi.org/10.1016/0040-1951(91)90501-I
- 22. Jónsson, S., Einarsson, P. and Sigmundsson, F. (1997) Extension across a Divergent Plate Boundary, the Eastern Volcanic Rift Zone, South Iceland, 1967-1994, Observed with GPS and Electronic Distance Measurements. Journal of Geophysical Research, 102, 11913-11929. http://dx.doi.org/10.1029/96JB03893
- 23. Venzke, E., Wunderman, R.W., McClelland, L., Simkin, T., Luhr, J.F., Siebert, L. and Mayberry, G. (2002) Global Volcanism, 1968 to the Present. Digital Inf. Ser., GVP-4, Global Volcanism Program, Smithson. Inst., Washington DC. http://www.volcano.si.edu/gvp/reports/
- 24. Okada, Y. (1985) Surface Deformation Due to Shear and Tensile Faults in a Half-Space. Bulletin of the Seismological Society of America, 75, 1135-1154.
- 25. Sigmundsson, F. (2006) Iceland Geodynamics: Crustal Deformation and Divergent Plate Tectonics. Praxis Publishing, Chichester.
- 26. Altamimi, Z., Collilieux, X., Legrand, J., Garayt, B. and Boucher, C. (2007) ITRF2005: A New Release of the International Terrestrial Reference Frame Based on Time Series of Station Positions and Earth Orientation Parameters. Journal of Geophysical Research, 112, 1-19. http://dx.doi.org/10.1029/2007JB004949
- 27. Savage, J.C. and Burford, R.O. (1973) Geodetic Determination of Relative Plate Motion in Central California. Journal of Geophysical Research, 78, 832-854. http://dx.doi.org/10.1029/JB078i005p00832
- 28. Gudmundsson, A. (1987) Tectonics of the Thingvellir Fissure Swarm, SW Iceland. Journal of Structural Geology, 9, 61-69. http://dx.doi.org/10.1016/0191-8141(87)90044-7
- 29. Behn, M.D., Boettcher, M.S. and Hirth, G. (2007) Thermal Structure of Oceanic Transform Faults. Geology, 4, 307- 310. http://dx.doi.org/10.1130/G23112A.1
- 30. Christensen, U. (1983) Convection in a Variable-Viscosity Fluid: Newtonian versus Power-Law Reheology. Earth and Planetary Science Letters, 64, 153-162. http://dx.doi.org/10.1016/0012-821X(83)90060-2
- 31. Pagli, C., Sigmundsson, F., Lund, B., Sturkell, E., Geirsson, H., Einarsson, P., et al. (2007) Glacio-Isostatic Deformation around the Vatnajokull Ice Cap, Iceland, Induced by Recent Climate Warming: GPS Observations and Finite Element Modelling. Journal of Geophysical Research, 112, 1-12. http://dx.doi.org/10.1029/2006JB004421
- 32. Jones, S.M. and Maclennan, J. (2005) Crustal Flow Beneath Iceland. Journal of Geophysical Research, 110, 1-19. http://dx.doi.org/10.1029/2004JB003592
- 33. Turcotte, D.L. and Schubert, G. (2002) Geodynamics. 2nd Edition, Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511807442
- 34. COMSOL Multiphysics (2013) COMSOL Documentation, Version 4.3.2.152.
- 35. Roland, E., Behn, M.D. and Hirth, G. (2010) Thermal-Mechanical Behavior of Oceanic Transform Faults: Implications for the Spatial Distribution of Seismicity. Geochemistry, Geophysics, Geosystems, 7, 1-15. http://dx.doi.org/10.1029/2010gc003034
- 36. Barnhoorn, A., van der Wal, W. and Drury, M.R. (2011) Upper Mantle Viscosity and Lithospheric Thickness under Iceland. Journal of Geodynamics, 52, 260-270. http://dx.doi.org/10.1016/j.jog.2011.01.002
- 37. Wu, P. (2004) Using Commercial Finite Element Packages for the Study of Earth Deformation, Sea Levels and the State of Stress. Geophysical Journal International, 158, 401-408. http://dx.doi.org/10.1111/j.1365-246X.2004.02338.x
- 38. Larson, M.G. and Bengzon, F. (2009) The Finite Element Method: Theory, Implementation, and Practice. Department of Mathematics, Ume University, Ume.
- 39. Fowler, C.M.R. (2005) The Solid Earth: An Introduction to Global Geophysics. 2nd Edition, Cambridge University Press, Cambridge.
- 40. Pálmason, G. (1986) Model of Crustal Formation in Iceland, and Application to Submarine Mid-Ocean Ridge. In: Vogt, P.R. and Tucholke, B.E., Eds., The Geology of North America: The Western North Atlantic Region, Geo-logical Society of America, Boulder, 87-97. http://dx.doi.org/10.1130/dnag-gna-m.87
- 41. Sigmundsson (2006)
- 42. Sturkell, E., Islam, M.T., Sigmundsson, F., Geirsson, H. and LaFemina, P.C. (2013) Continuous Subsidence in the Thinvellir Rift Graben, Iceland: Geodetic Observations since 1996 Compared to Rheological Models of Plate Spreading [abs]. AGU Fall Meeting, 1810891.
- 43. Hirsch, M.W., Smale, S. and Devaney, R.L. (2004) Phase Portraits for Planar Systems, in Differential Equation, Dynamical Systems & an Introduction to Chaos. 2nd Edition, ELSEVIER Academic Press, California.







