Open Journal of Social Sciences
Vol.03 No.07(2015), Article ID:57985,6 pages
10.4236/jss.2015.37011
Intraday Periodicity and Long Memory Volatility in Hong Kong Stock Market
Wei Dai, Dejun Xie, Bianxia Sun
Department of Financial Mathematics and Financial Engineering, South University of Science and Technology of China, Shenzhen, China
Email: daiw@mail.sustc.edu.cn, xiedj@sustc.edu.cn, sunbx@sustc.edu.cn


Received 1 April 2015; accepted 11 July 2015; published 14 July 2015

ABSTRACT
This paper characterizes the volatility in Hong Kong Stock Market based on a 2-year sample of 5-min Heng Seng Index. By using the method of Flexible Fourier Form Filtering, we have successful removed the periodicity and have built a model of ARMA (1,1)-FIAPARCH (2, 0.300165,1). Further, the intraday volatility exists with long memory and asymmetry; the negative shock from the market will give rise to a higher volatility than the positive ones.
Keywords:
Volatility, High Frequency Data, Periodicity, Long Memory

1. Introduction
An extensive literature has characterized the systematic features of return volatility at the daily and lower frequencies for all major primary financial assets, including foreign exchange, equity, fixed-income, and commodity related securities, although there are some important differences across this diverse set of assets. The qualitative findings are remarkably uniform, enabling a variant of the nonlinear time-series models within the stochastic volatility and ARCH class to provide a good first-order approximation to the underlying volatility dynamics in practically all cases, see Bollerslev et al. (1992) [1] and Ghysels et al. (1995) [2].
Some research focuses on the volatility-volume relationship in contemporaneous period. Karpoff (1987) [3] reviews lots of papers studying the volatility and volume and points out that the positive correlation relationship exists between the two market variables. Lamoureu and Lastrapes (1990) [4] initially apply the GARCH model into the study on 20 stocks traded in NYSE and find that stock return volatility is positively influenced by trading volumes. Among others, Majand and Yung (1991) [5] and Sharma et al. (1996) [6] use different models in different financial markets and basically come to the same conclusion on the positive influence of trading volume on return volatility.
The purpose of this paper is to focus on the properties of high frequency trading data in Hong Kong. To identify what is the difference between Hong Kong and any other markets, we use a method of FFF and build up a model on volatility, which is very useful for investors involved in the quality trading and interested in Hong Kong Stock Market.
This paper is organized as follows. Data description and preliminary analysis are presented in Section 2. The methodology to build up a model and the empirical results are explained in Section 3. Section 4 gives a conclusion.
2. Data and Intraday Periodicity
2.1. Data
The sample we selected is five minute return of HSI (Heng Seng Index), for the following reasons. First, HSI is a capitalization-weighted stock market index in Hong Kong, It is used to record and monitor daily changes of the largest companies of the Hong Kong Stock Market, which is the significant indicator of the overall market performance in Hong Kong. Second, the sample frequency we choose to be 5 minutes is based on the research proposed by Hansen and Lunde (2006) [7], they showed as the sample frequency increased, the problems result from the market microstructure noise will be more serious. In order to balance the issue of accuracy and noise, 5 minutes return will be the most suitable choice, showed by Andersen (2001) [8] and Koopman (2005) [9]
The intraday HSI data covers the 2-year-period from March 26, 2012 to December 30, 2013. We partitioned the series into 5-min intervals and computed continuously compounded returns based on the last quotation within each interval. The daily interval covers the period from 9:20 a.m. to 12:00 a.m., 13:00 p.m. to 16:00 p.m. The initial return of the trading day, 9:20-9:25, largely reflects the adjustment to information accumulated overnight, and consequently displays a much lower average return variability than any other 5-min interval. In order not to confound our statistical inference, we deleted this “unusual” return interval. This leaves us with a sample of 427 trading days, each consisting of 67 intraday 5-min returns.
2.2. The Descriptive Statistics of 5-Minute Return
The daily return 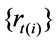 is calculated by
is calculated by
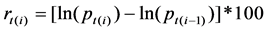 (1)
(1)
where, represents the index on the moment i, t day. In this paper, we mainly focus on the property of daily return volatility, so the daily overnight return (the return between the daily closing price and following open price) is out of our consideration.
As Table 1 shows, the sample mean of this 5-min return series equals 0.00068, given the standard deviation of 0.083, the high-frequency mean return is effectively zero from a statistical perspective. On the other hand, the p-value of Q-statistics on both raw data and square data are all less than 0.05, which means the five-min return and volatility exists strong autocorrelation and has the ARCH effect.
Figure 1 depicts the raw and absolute returns over the 427 trading days. The raw return appear to be systematically lower at the opening and then tend to be fluctuate around 0, but increase towards the end of the trading day and finally decrease. A similar tendency for low returns at the open and close have been documented for SHSZ300 Index returns by Bianxia Sun [10].
In contrast, the average absolute returns in Figure 1(B) display a strikingly regular pattern. Starting out about 0.22% in the morning, they drop almost quarter during the late morning and afternoon session. Specially, there are two bulges associated with the lunch break and the close time separately, both of these two bulges are increase at first and then decrease rapidly, which is different from the Japanese Market, showed by Andersen and Bollerslev (2000) [11], the absolute return in Japanese market stays high level at both the beginning and closing time.
Turning to the time-series dependencies, Figure 2 plots the auto correlograms for the absolute returns with a lag of 340 5-min intervals, or 5 trading days. For the absolute returns all of the autocorrelations in Figure 2 displays a pronounced repetitive pattern. These results are in line with the earlier evidence in Andersen and Bollerslev pertaining to the US equity and foreign exchange markets. Because of this strong periodicity, Standard ARCH and stochastic volatility models, which generally imply a monotone geometric decay in the autocorrelation of the absolute returns, are not directly applicable.
3. Modeling the Volatility
3.1. Periodicity
In order to address this issue, we rely on the general frame work developed by Andersen and Bollerslev (1997b,

Figure 1. Five-minute return of HIS.
Figure 2. ACF squared 5-min return.
Table 1. The descriptive statistics of data.
1998a) [12] for analyzing high-frequency return series. The basic idea involves the following decomposition
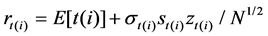 (2)
(2)
where N denotes the number of high-frequency returns per day, 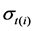 is intended to capture the overall volatility level on day t,
is intended to capture the overall volatility level on day t,  refers to the periodic intraday volatility component, and
refers to the periodic intraday volatility component, and  is an i.i.d mean zero, unit variance error term,
is an i.i.d mean zero, unit variance error term,  is the expectation of return
is the expectation of return
To separate the periodic factor from the equation, let move 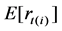 to the left side, square it and then take logarithmic on the equation , we can get
to the left side, square it and then take logarithmic on the equation , we can get
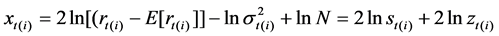 (3)
(3)
In application, first, we need to estimate 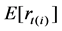 and
and  to make the left side of the equation available. Suggested by Anderse and Bollerslev (1997), the sample mean
to make the left side of the equation available. Suggested by Anderse and Bollerslev (1997), the sample mean 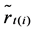 can be used to replace
can be used to replace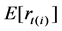 ,
,




By using the method of OLS,

where

where t refers the observation date, 









Figure 3 represents the ACF-Squared 5-min return after deseasonalizing by using the method proposed above. Clearly the periodicity do not exists any longer.
3.2. Modeling the Volatility
To take into account asymmetric responses of volatility to positive and negative shocks along with volatility persistence behavior, Tse (1998) [13] extended the Asymmetrc Power GARCH model of Ding, Granger and Engle (1993) [14] by incorporating a fractional filter in the conditional variance equation. The obtained model is known as FIAPARCH.
Figure 3. ACF squared deseasonalized 5-min FFF returns.
In the following, we present the ARFIMA-FIAPARCH model which generates long memory properties in both the first and the second conditional moment. In this dual long memory framework, in the conditional mean, we fit a ARFIMA (p,d,q) specification given formally by

where 





where 




When

3.3. Selection of the Optical Lag
In terms of the lag order selection of model ARFIMA (p, dm, q)-FIAPARCH (P,dv,Q). We decide to use the method of “Identify” “Estimate” and “Diagnosis”. Fist, in order to get the ARFIMA (p,dm,q) model, we choose the most suitable lag with the minimum AIC. Second, the same method to determine the lag of FIAPARCH (P, dv, Q). Finally, after the model has been established, the residuals should be checked by using Ljung-Box. If we can not reject the null hypothesis that the data exists autocorrelation under the significance level of 5%, we will see the model is fine. Once the check has been rejected, we should restart it from the beginning.
3.4. Estimation Results
According to the method proposed above, we determine to establish the model of ARMA (1,1)-FIAPARCH (2,dv,1), More details about the estimation results, reported as Table 2.
The parameter of dv is used to measure the long memory of volatility. In the model, dv is estimated to be 0.300165 and showed to be significant under the level of 5%, which represents, the five-min return of HSI has the property of long memory in volatility,
Empiricalresearch has showed asset daily return are usually information asymmetric. In our case, 

Table 2. Estimation results of ARMA-FIAPARCH.
4. Conclusion
This paper provides a detailed characterization of volatility in Hong Kong Stock Market based on a long sample of high-frequency 5-min Heng Seng Index returns. Our major findings are as follows: different from other stock markets like Japan that the intraday volatility is not acting as completely U-shaped Pattern, what is special in Hong Kong Stock Market is the volatility tending to decrease dramatically at the closing time. Meanwhile, the high frequency data contain very useful information about the salient long-lived interdaily volatility dependencies. This long-memory component in turn explains most of the day to day variation in Heng Seng volatility. Our results further show that in Hong Kong Stock Market, the negative information will give rise to a higher volatility than the positive ones.
Cite this paper
Wei Dai,Dejun Xie,Bianxia Sun, (2015) Intraday Periodicity and Long Memory Volatility in Hong Kong Stock Market. Open Journal of Social Sciences,03,61-66. doi: 10.4236/jss.2015.37011
References
- 1. Bollerslev, T., Chou, R.Y. and Kroner, K.F. (1992) ARCH Modeling in I’inance. Journal of Econometrics, 52, 5-59. http://dx.doi.org/10.1016/0304-4076(92)90064-X
- 2. Ghysels, E., Harvey, A. and Renault, E. (1995) Stochastic Volatility. CIRANO.
- 3. Karpoff, J.M. (1987) The Relation between Price Changes and Trading Volume: A Survey. Journal of Financial and Quantitative Analysis, 22, 109-126.
- 4. Lamoureux, C.G. and Lastrapes, W.D. (1990) Persistence in Variance, Structural Change, and the GARCH Model. Journal of Business & Economic Statistics, 8, 225-234.
- 5. Majand, M. and Yung, K. (1991) A GARCH Examination of the Relationship between Volume and Price Variability in Futures Markets. Journal of Futures Markets, 11, 613-621. http://dx.doi.org/10.1002/fut.3990110509
- 6. Sharma, J.L., Mougoue, M. and Kamath, R. (1996) Heteroscedasticity in Stock Market Indicator Return Data: Volume versus GARCH Effects. Applied Financial Economics, 6, 337-342.
- 7. Hansen, P.R. and Lunde, A. (2006) Realized Variance and Market Microstructure Noise. Journal of Business & Economic Statistics, 24, 127-161. http://dx.doi.org/10.1198/073500106000000071
- 8. Andersen, T.G., Bollerslev, T., Diebold, F.X., et al. (2001) The Distribution of Realized Stock Return Volatility. Journal of Financial Economics, 61, 43-76. http://dx.doi.org/10.1016/S0304-405X(01)00055-1
- 9. Koopman, S.J., Jungbacker, B. and Hol, E. (2005) Forecasting Daily Variability of the S&P 100 Stock Index Using Historical, Realised and Implied Volatility Measurements. Journal of Empirical Finance, 12, 445-475.
- 10. 孙便霞, 西村友作 (2012) 沪深300股指期货的日内动态特征分析. 上海金融, 12, 80-83.
- 11. Andersen, T.G., Bollerslev, T. and Cai, J. (2000) Intraday and Interday Volatility in the Japanese Stock Market. Journal of International Financial Markets, Institutions and Money, 10, 107-130. http://dx.doi.org/10.1016/S1042-4431(99)00029-3
- 12. Andersen, T.G. and Bollerslev, T. (1998) Answering the Skeptics: Yes, Standard Volatility Models Do Provide Accurate Forecasts. International Economic Review, 885-905.
- 13. Tse, Y.K. (1998) The Conditional Heteroscedasticity of the Yen-Dollar Exchange Rate. Journal of Applied Econometrics, 13, 49-55. http://dx.doi.org/10.1002/(SICI)1099-1255(199801/02)13:1<49::AID-JAE459>3.0.CO;2-O
- 14. Ding, Z. and Granger, C.W.J. (1996) Modeling Volatility Persistence of Speculative Returns: A New Approach. Journal of Econometrics, 73, 185-215. http://dx.doi.org/10.1016/0304-4076(95)01737-2






