Journal of Applied Mathematics and Physics
Vol.03 No.07(2015), Article ID:57952,8 pages
10.4236/jamp.2015.37105
Fundamental Research of Wave Phenomenon in Frozen Rock Massif during Shaft Sinking
I. M. Palankoev
President of Joint-Stock Company (UMC “Souz Spec Stroy”), Moscow, Russia
Email: mishkenzia@gmail.com


Received 20 February 2015; accepted 8 July 2015; published 15 July 2015

ABSTRACT
Shaft sinking in frozen soils with adoption of blasting for rocks ripping in some cases leads destruction of freezing columns. Such damages are coincided to rocks interface. At the same time, in case rock stratification is absent in geological section, rapture of freezing columns never has a place. Physical explanation of this phenomenon is possibly on the base of wave processes, which having place in specific conditions of shaft sinking with adoption of blasting works.
Keywords:
Ground Freezing, Blasting, Freezing Columns, Acoustic Stiffness

1. Introduction
Review of theoretical studies, concerning to a problem of negative development’s investigation of concomitant to the ground freezing process in shafts, and shows, that deformation of freezing columns often coincided with a regions of interbedded layers of frozen rocks with different acoustic stiffness, such as frozen sands and clays. But reason of this phenomenon is not explained [1].
This article will show the results of researches which explain appear of thickness resonance inside the vertical nonhomogeneous layer, abutting to later face of built shaft. And it will gives appraisal of feature distribution of normal waves in the waveguide generated between the free surface of pit bottom and a horizontal interface throughout the height for the heterogeneous waveguides. Critical thickness of the waveguide that leads to deformations of the frozen columns has been discovered.
2. Problem Formulation
Presence of horizontal interface of soils with different acoustic stiffness, lower pit bottom, creates prerequisites for beginnings of waveguide zone with drastic horizontal interfaces. Lower bound of this waveguide is an interface with different type soils, such as our example between frozen water-logged sand and clay. And the upper bound is a rock face, it is absolutely soft wall with reflection factor = 0 on pressure V [3].
Length of waveguide is correspond to the rock face (L = D = 7 m). At the both ends of waveguide, it mates with vertical layer with thickness hv, with dissimilar surface.
Altitude of horizontal waveguide hg depending on shaft sinking technology and can range between 2 and 4 m [2]. Thus is can be given a ration of waveguide and layer thicknesses: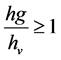 . Physical analog of an object in the case being considered in horizontal profile presented in Figure 1.
. Physical analog of an object in the case being considered in horizontal profile presented in Figure 1.
To make a characteristic of low bound, and consequently a classification of its type, we will estimate reflection index from this bound.
Under variation of longitudinal waves speed in frozen clay over the range 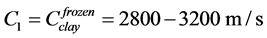 and in frozen sand
and in frozen sand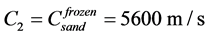 , refraction coefficient of P-waves, is:
, refraction coefficient of P-waves, is:  and clay
and clay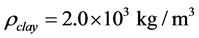 .
.
Average value n = 0.536, taking in account density of frozen sand 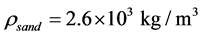 , their ratio will be
, their ratio will be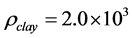 .
.
In this case, pressure refractive index will be 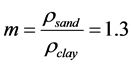 [5]
[5]

Consequently, low bound can be taken as a “strong” bound, and this waveguide, by ratio of its compounded mediums acoustic characteristics, is similar to so-called near surface sound channel, with a free upper bound (where upper bound-air) and lower drastic bound , on which n ˂ 1.
During the blasting of explosive charge, on each waveguide’s end (solution of the problem is in plane) inside of it, appears composite interference wave field, which theoretically, composed of infinite sum of normal waves with different numbers of l. Each normal wave number l is running lengthwise waveguide axis (lengthwise axis X) with its oven phase velocity Cl, which depends on the number of wave l, frequency of the source f, height of waveguide h and medium properties inside the waveguide.
At the same time each normal wave number l is stagnant along the thickness of waveguide h (lengthwise axis Z), i.e. amplitude of each normal wave number l congruence 0. For example, in the simplest case, when reflectance from low absolutely rigid bound V2 = 1, and reflectance from upper interface V1 = −1, as in the current task, then wave potential Ψ inside of the waveguide [1] [4]
Figure 1. An object of physical analog assumes the presence of horizontal interface.
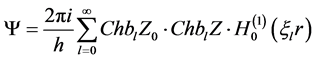 (1)
(1)
where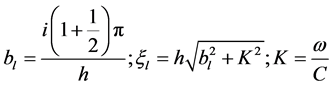 .
.
Z0-position of a point source; Z?position of observation point;
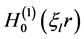 -Hankel transform
-Hankel transform
Each normal wave number l propagates lengthwise the layer with a speed:
 (2)
(2)
where C-speed of waves in medium of the waveguide; 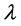 -wavelength,
-wavelength,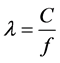 .
.
In the case under consideration, lower bound of waveguide is characterized by the absolute number of reflectance V1, which in general can be calculated so:
 (3)
(3)
where 

Similar formula can be given for reflectance from the second bound V2. In case if waveguide has two bounds with arbitrary index of reflectance V1 and V2, then more generally normal wave field inside the waveguide can be written so:

where b = ikcosϴ; ϴl―roots of dispersion equation

When the upper bound is absolutely soft (V2 = −1), in a rather big distances from the radiator (

where Z0, Z―radiator’s and detector’s location.

It being understood that wave field inside the waveguide springs up by point (spherical) source:

where A―vibration altitude of a source;
Q0―volume velocity;
S―radiating area,
V―particle velocity on a sphere.
Hereinafter amplitude of primary field will equals to unit (A0 = 1)
Xl is the root of dispersion equation:

where

Each normal wave number l is characterized by her distribution of waves amplitude through the thickness of the waveguide (lengthwise axis Z), her phase velocity Cl and absorption factor

To assess traits of normal waves distribution, which are created by explosion source inside the waveguide between the free surface of pit bottom and horizontal interface, we made calculations of first free normal waves amplitude distribution (l = 1, 2, 3) with waveguide height (

When caring out calculations, where considered only average waveguide characteristics 



In this case
The value of dispersion equation root for normal waves number l = 1, 2, 3 was calculated on the base of graphic solutions by congruent curve. Calculations were made for waveguides with height 
Table 1. Characteristics of the waveguide and normal waves with different number l.
To assess the possibility of excitation by each acoustic mode of thickness resonance in vertical layer with heterogeneous interface, where calculated ankles:

3. Model and Simulation Result
As a physical analog of item involved, we choose so-cold “acoustic medium”, in which are considered just longitudinal acoustic waves. Task solution is given in the plane same to profile of an object. To assess the possibility of thickness resonance excitation by each acoustic mode in the vertical layer with heterogeneous interface were calculated amplitudes of first three waves and angles of incidence on the heterogeneous layer.
Calculations were made in software Mathcad by ranking method.
Results of calculations are shown in Figures 2-7.
From derived distributions Al = f(Z) it is clear, that the biggest amplitude in the waveguide’s sectional view will be in all instances of main normal wave with l = 1. Besides, in all instances, first mode amplitude’s splitting form in sectional view of a waveguide is approximate to piston valve gear. Value of ankle ϴl is shown in Table 2.
That is why hereinafter we will analyze behavior just of first two modes (l = 1 and l = 2) under changing of waveguide’s height. Values of maximum amplitude for the first two modes of a waveguide, with different height h, are shown in Table 3.
Figure 2. First normal wave amplitude distribution according to a height of a waveguide (
Table 2. Angle ϴl according to h.
Figure 3. First two normal wave’s amplitude distribution according to a height of a waveguide
Figure 4. First two normal wave’s amplitude distribution according to a height of a waveguide
Figure 5. First three normal wave’s amplitude distribution according to a height of a waveguide
Figure 6. First two normal wave’s amplitude distribution according to a height of a waveguide
Figure 7. First two normal wave’s amplitude distribution according to a height of a waveguide
Table 3. Dependence of maximum amplitude Al from a waveguide’s thickness.
It is apparent from Table 3 that then less is the height of waveguide h, then bigger is the maximum amplitude of the main mode. On increasing of a waveguide’s height up to h = 3, amplitude A1(h) will slight decrease. And just for a waveguide with h = 4 there is a sudden amplitude decrease. Thus, ratio of amplitude Al of a waveguide with h = 2 m to the same amplitude for a waveguide with h = 4 m is more than 5 times. Besides, waveguide with h = 4 m has a different main mode amplitude pattern over a cross section?it changes into a double-humped distribution.
4. Discussion and Conclusion.
From this article, it may be inferred that the pronounced canalization of the wave energy from the radiator which inside the waveguide can be seen when the varying of distance from the pit bottom to a vertical interface in the range of 0.5 to 3 m and the distance h > 4 m this wave effect is practical insignificant.
From the results of this study I suppose to ensure practical guidance on the betterment of the shaft sinking technology with adoption of ground freezing method. On application of blasting workings during shaft sinking, in case of existence of interface between frozen soils in front of a pit bottom, to avoid possible destruction of freezing columns, we recommend to use blasting just in a distance not less than 4 meters between the pit bottom and horizontal interface [6].
To increase the probability of trouble-free operation of blasting works I suppose that the stowage of explosive should at the depth of 0.5 m from pit bottom face. When shaft sinking in a distance is less than 4 m to the rock interface it is important to use another shaft sinking method in frozen rocks, such as create of a relieve slot by the help of compensation holes.
Cite this paper
I. M. Palankoev, (2015) Fundamental Research of Wave Phenomenon in Frozen Rock Massif during Shaft Sinking. Journal of Applied Mathematics and Physics,03,846-853. doi: 10.4236/jamp.2015.37105
References
- 1. Brekhovskikh, L.M. (1957) Waves in Stratified Mediums. Publishing House of The Academy of Science.
- 2. Voyt, S.S. (1953) Reflection and Refraction of Spherical Acoustic Waves in Stationary-Moving Mediums Transition. Applied Mechanics, 17, 157.
- 3. Ivanovsky, V.N. and Kashtanov, V.S. (2006) Oil and Gas Equipment. High School Textbook, Gubkin RSU of Oil and Gas, Moscow, 720.
- 4. Krukov, G.M. and Glazkov, Y.V. (2003) Phenomenological Qua-si-Static Wave Theory of Deformation and Fracture of Material by Industrial Explosive Blasting. Publishing House of Moscow State Mining University.
- 5. Lependin, L.F. (1978) Acoustic. Publishing House “Visshaya skola”, Moscow.
- 6. Palankoev, I.M. (n.d.) Method of Shaft Sinking in Unstable and Water Flooded Rocks. Patent of Russian Federation No. 2534274.












