Received 6 May 2015; accepted 7 July 2015; published 14 July 2015

ABSTRACT

We consider the singularly perturbed sixth-order Boussinesq-type equation, which describes the bidirectional propagation of small amplitude and long capillary gravity waves on the surface of shallow water for bond number (surface tension parameter) less than but very close to 1/3. The sufficient conditions of blow-up of solution to the Cauchy problem for this equation are given.

Keywords:

Singularly Perturbed Sixth-Order Boussinesq Equation, Cauchy Problem, Blow-Up of Solution

1. Introduction

In this paper, we consider the following Cauchy problem

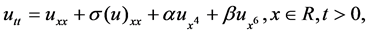(1.1)

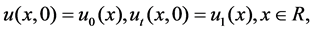(1.2)

where 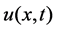is the unknown function, 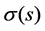is the given function, 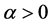and 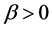are real numbers, 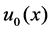and 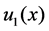are given initial value functions.

In [1], the author has proved the existence and uniqueness of the global generalized solution and the global classical solution for the initial boundary value problem of Equation (1.1).

In [2], the author has discussed the nonexistence of global solution to the initial boundary value problem of Equation (1.1) in some condition.

In order to prove that blow-up of Cauchy problem (1.1), (1.2), we shall consider the following auxiliary problem

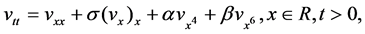(1.3)

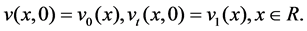(1.4)

Then, we can obtain blow-up of the Cauchy problem (1.1), (1.2) from (1.3), (1.4) by setting,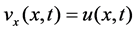

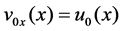and.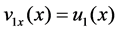

2. Main Theorems

Throughout this paper, we use the following notation: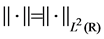. Now, we give the following main lemmas and theorems.

Lemma 2.1 (convex lemma [3]) Suppose that a positive twice-differential function 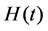satisfies on 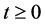the inequality

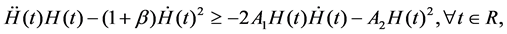(2.1)

where and are constants,.

(1) If and, then there exist a, such that as .

(2) If and, then as, where

and

Lemma 2.2 [4] Suppose that, then may be embedded into, and for any, we have

where is a set of nonnegative integers.

Lemma 2.3 Suppose that and, then the solution of the auxiliary problem (1.3), (1.4) satisfies the following energy identity

(2.2)

Proof Multiplying both sides of (1.3) by, integrating on, integrating by parts and lemma 2.2, we get

integrating the product over, we get the identity (2.2).

Theorem 2.1 Suppose that, and there exists

constant and, such that

(2.3)

Then, the solution of the auxiliary problem (1.3), (1.4) blows-up in finite time if one of the following conditions holds

(1)

(2)

(3)

Proof Suppose that the maximal time of the solution for (1.3), (1.4) is infinite. Let

(2.4)

where and are undetermined nonnegative constants. Differentiating (2.4) with respect to, we have

(2.5)

By using the Hölder inequality, it follows from (2.5) that

(2.6)

Differentiating (2.5) with respect to, making use of (1.3) and (2.2), we get

(2.7)

By virtue of interpolating inequality,

Observing the identity (2.7), we get

(2.8)

Combing (2.2), (2.3), (2.4), (2.6) with (2.8), we infer

(2.9)

(1) If, by taking, then

When is sufficiently large,. Clearly,. It follows from lemma (2.1) that there exists, such that as.

(2) If, by taking, we get

By virtue of assumption (2), we see and. It follows from lemma (2.1) that there exists, such that as.

(3) If, by taking, (2.9) becomes

Defining

then

(2.10)

By virtue of assumption (3), we have. Let

Thanks to the continuity of, is a positive number. Multiplying both sides of (2.10) by, we find

(2.11)

Integrating (2.11) with respect to over, one gets

By virtue of assumption (3), we see that

Since is a continuous function, we have for,

(2.12)

It follows from the definition of that (2.12) holds for all. Integrating (2.12) with respect to, we arrive at

Hence there is some, such that, where

So becomes infinite at.

Thus, always becomes infinite at under the assumption (1) or (2) or (3). This is a contradiction to the fact that the maximal time of existence of the solution is infinite. The theorem is proved.

Theorem 2.2 Suppose that, and there exist constant and, such that

Then, the solution of the Cauchy problem (1.1), (1.2) blows-up in finite time if one of the following conditions holds

(1)

(2)

(3)

where

Proof Let

where and are nonnegative constants as those in Theorem 2.1.

By virtue of assumption Theorem 2.1, satisfies the Equation (1.1) and the initial value condition (1.2) in classical sense. We take the change

(2.13)

Then

Substituting the above change (2.13) to the Cauchy problem (1.1), (1.2), we have

(2.14)

(2.15)

Integrating (2.14) and (2.15) over, we obtain

(2.16)

(2.17)

Let

where and are nonnegative constants as those in Theorem 2.1. By virtue of assumption Theorem 2.1, the sufficient conditions of blow-up of solution to the Cauchy problem (2.16), (2.17) are fulfilled. Therefore, It follows from theorem 2.1 that becomes infinite at Since by the change (2.13), , so becomes infinite at. Theorem 2.2 is proved.

Fund

This project is supported by NSF Grant 11271336, NSF of Henan Province Grant 122300410166.

Cite this paper

Changming Song,Li Chen, (2015) Blow-Up of Solution to Cauchy Problem for the Singularly Perturbed Sixth-Order Boussinesq-Type Equation. Journal of Applied Mathematics and Physics,03,834-838. doi: 10.4236/jamp.2015.37103

References