Communications and Network, 2009, 20-24
doi:10.4236/cn.2009.11003 Published Online August 2009 (http://www.scirp.org/journal/cn)
Comparison and Design of Decoder in B3G Mobile
Communication System
Mingxiang GUAN1, Mingchuan YANG2
1Department of Electronic Communication Technology, Shenzhen Institute of Information Technology, Shenzhen, China
2School of Electronic and Information Technology, Harbin Institute of Technology, Harbin, China
Abstract: Turbo code has been shown to have ability to achieve performance that is close to Shannon limit. It
has been adopted by various commercial communication systems. Both universal mobile telecommunications
system (UMTS) TDD and FDD have also employed turbo code as the error correction coding scheme. It out-
performs convolutional code in large block size, but because of its time delay, it is often only used in the
non-real-time service. In this paper, we discuss the encoder and decoder structure of turbo code in B3G mo-
bile communication System. In addition, various decoding techniques, such as the Log-MAP, Max-log-MAP
and SOVA algorithm for non-real-time service are deduced and compared. The performance results of de-
coder and algorithms in different configurations are also shown.
Keywords: decoder, beyond 3G mobile communication system, decoding algorithm
1. Introduction
A turbo code can be thought as a refinement of the con-
catenated encoding structure and an iterative algorithm
for decoding the associated code sequence [1]. The codes
are constructed by applying two or more component
codes to different interleaved versions of the same in-
formation sequence [2][3]. In literature [4], for any single
traditional code, the final step at the decoder yields
hard-decision decoded bits (or, more generally, decoded
symbols). In order for a concatenated scheme such as a
turbo code to work properly, the decoding algorithm
should not limit itself to pass hard decisions among the
decoders [5]. To best exploit the information learned
from each decoder, the decoding algorithm must effect
an exchange of soft rather than hard decisions [6]. For a
system with two component codes, the concept behind
turbo decoding is to pass soft decisions from the output
of one decoder to the input of the other, and to iterate this
process several times to produce better decisions [7].
2. Principle of Iterative Decoding
For the first decoding iteration of the soft input/soft out-
put decoder in Figure 1, one generally assumes the bi-
nary data to be equally likely, yielding an initial a priori
LLR value of L(d) =0 for the third term in [8]. The
channel pre-detection LLR value, Lc(x) , is measured by
forming the logarithm of the ratio o1
f

and 2

, seen
in Figure l. The outputˆ)
of the Figure 2 decoder is
made up of the LLR from the detector, , and the
extrinsic LLR output. , representing knowledge
gleaned from the decoding process. As illustrated in Fig-
ure 2, for iterative decoding the extrinsic likelihood is fed
back to the decoder input, to serve as a refinement of the
a priori value for the next iteration.
Consider the two-dimensional code (product code) de-
picted in Figure 2. The configuration can be described as
Figure 1. Soft input/soft output decoder
(Ld
ˆ
(
e
Ld
ˆ
'( )Ld
)
This paper supported by the 3rd natural science foundation of institute
(No. LG-08010). Figure 2. Two-dimensional product code

COMPARISON AND DESIGN OF DECODER IN B3G MOBILE COMMUNICATION SYSTEM 21
a data array made up of k1 rows and k2 columns. Each of
the k1 rows contains a code vector made up of k2 data bits
and n2-k2 parity bits. Similarly, each of the k
2 columns
contains a code vector made up of k1 data bits and n1-k1
parity bits. The various portions of the structure are la-
beled d for data, ph for horizontal parity (along the rows),
and pv for vertical parity (along the columns). Addition-
ally, there are blocks labeled Leh and L
ev , which house
the extrinsic LLR values learned from the horizontal and
vertical decoding steps, respectively. Notice that this
product code is a simple example of a concatenated code.
Its structure encompasses two separate encoding steps,
horizontal and vertical. The iterative decoding algorithm
for this product code proceeds as follows:
1) Set the a priori information
L(d)=0 (1)
2) Decode horizontally, obtain the horizontal extrinsic
information as shown below:
ˆˆ
()()() ()
eh c
LdLdLx Ld  (2)
3) Set
ˆ
() ()
eh
LdL d (3)
4) Decode vertically, obtain the vertical extrinsic in-
formation as shown below:
ˆˆ
()()() ()
ev c
LdLdLxLd  (4)
5) Set
ˆ
()()
ev
LdL d (5 )
6) If there have been enough iterations to yield a reli-
able 7 decision, go to step 7; otherwise, go to step 2;
7) The soft output is:
ˆˆ
() ()()()
ceh ev
LdL xLdLd 
ˆ
(6)
3. B3G Mobile System Decoder Design
The algorithms for decoders can be divided into two
categories: (1) Log-MAP: Log-Maximum A Posteriori,
(2) SOVA: Soft Output Viterbi Algorithm.
3.1. Log-MAP Algorithm
Before explaining the MAP decoding algorithm, we as-
sume some notations:
()
S
k
s
e starting stage of the edge e.
()
E
k
s
e ending stage of the edge e.
dk(e) the information word containing k0 bits.
ui stands for individual information bits.
xk(e) codeword containing n0 bits.
We assume here that the received signal is yk=xk+n
(transmitted symbols + noise).
The metric at time k is
()((),|())
(()|())(| ())(|)
k
EE
kkkk
ES S
kk kkkk
x
Mepsey xe
psesepxsepyx

 (7)
(()
E
k
pse |()
S
k
s
e) a priori information of the informa-
tion bit.
(|())
S
kk
pxs e
k
indicating the existence of connection
between edges()
S
s
e,()
E
k
s
e
(|)
kk
pyx probability of receiving yk if xk was trans-
mitted.
Ak(.) and Bk(.) is forward and backward path metrics.
1
1
:()
()( (),)
(( ))( ),1,...,1
E
k
Ek
kk
S
kk k
es e s
Asps esy
AseMek N






(8)
11
11 1
:()
()(|())
(())( ),,...,1
E
k
kS
kk
S
kk k
es e s
Bspy ses
BseMekN





 (9)
Suppose the decoder starts and ends with known states
0
0
1, 1,
()()
0, 0,
N
N
sS sS
AsB s
otherwise otherwise





， (10)
If the final state of the trellis is unknown:
1
() ,
2
Nm
Bs s

 (11)
The joint probability at time k is:
11
()(,)( ()).(). (())
NS E
kkkk
epeyAseMeBse 

 kk (12)
3.2. Output Viterbi Algorithm (SOVA)
There are two modifications compared to the classical
Viterbi algorithm. One is the path metric modified to
account the extrinsic information. This is similar to the
metric calculation in Log-MAP algorithm. The other is
the algorithm modified to calculate the soft bit. For each
state in the trellis the metric ()
S
k
M
s is calculated for
both merging paths, the path with the highest metric is
selected to be the survivor, and for the state (at this stage)
a pointer to the previous state along the surviving path is
stored. The information to give L(uk|y) is stored, the dif-
ference i
s
k

between the discarded and surviving path.
The binary vector containingδ+1 bits, indicating last δ+1
bits that generated the discarded path. After ML path is
found the update sequences and metric differences are
used to calculate L(uk|y). For each bit
M
L
k
u in the ML
path, we try to find the path merging with ML path that
had compared to the
M
L
k
u in ML different bit value uk at
state k and this path should have minimal distance with
ML path. We go trough δ+1 merging paths that follow
C opyright © 2009 SciRes CN

22 COMPARISON AND DESIGN OF DECODER IN B3G MOBILE COMMUNICATION SYSTEM
stage k i.e. the i
s
k
 i = k,…, (k +δ), for each merging
path in that set we calculate back to find out which value
of the bit uk generated this path. If the bit uk in this path is
not
M
L
k
u and i
s
k
 is less than current , we set
=.
min
k

min
k
i
s
k

...
(|y)min i
ML i
kk
S
kk i
ik k
uu
u
 

Lu ( 13)
4. Comparison of the Decoding Algorithms
SOVA the ML path is found. The recursion used is iden-
tical to the one used for calculating of α in Log-MAP
algorithm. Along the ML path hard decision on the bit uk
is made. L(uk|y) is the minimum metric difference be-
tween the ML path and the path that merges with ML
path and is generated with different bit value uk. In L(uk|y)
calculations accordingly to Log-MAP one path is ML
path and other is the most likely path that gives the dif-
ferent uk. In SOVA the difference is calculated between
the ML and the most likely path that merges with ML
path and gives different uk. This path but the other may
not be the most likely one for giving different uk. Com-
pared to Log-MAP output (SOVA does not have bias),
the output of SOVA is just much noisier. The SOVA and
Log-MAP have the same output. The magnitude of the
soft decisions of SOVA will either be identical of higher
than those of Log-MAP. If the most likely path that gives
the different hard decision for u
k, has survived and
merges with ML path the two algorithms are identical. If
that path does not survive the path on what different uk is
made is less likely than the path which should have been
used.
The forward recursion in Log-MAP and SOVA is
identical but the trace-back depth in SOVA is either less
than or equal to the backward recursion depth. Log-MAP
is the slowest of the three algorithms, but has the best
performance among these three algorithms. In our
TD-CDMA simulation, we implemented the Log-MAP
and SOVA decoder to get best performance (with Log-
MAP) or fastest speed (with SOVA). Figure 3 gives the
performance comparison between Log-MAP and SOVA
and it shows that Log-MAP is 1.2dB better than SOVA
at the BER of 10-2, with the code block size of 260 bits
and 7 iterations.
The code block size or interleaver size is also affect
the decoding performance, the BER performance com-
parison of various code block size is shown in Figure 4.
The longer is the code block, the better is the perform-
ance, but the big code block size makes more computing
time, and the computing complexity increases by expo-
nential.
Table 1. Comparison of complexity of different decoding
algorithms
Operations MAP Log-MAP SOVA
additions 4×2M+6 12×2M+6 4×2M+9
max-ops 4×2M-2 2×2M-1
multiplications 10×2M+8 8 4
look-ups 4(exp) 4×2M-2
Figure 3. BER performance of Log-MAP algorithm VS SOVA algorithm
Log-MAP
SOVA
BER
Eb/N0
1.5
1
0.5
10-4
0
10-3
10-2
10-1
100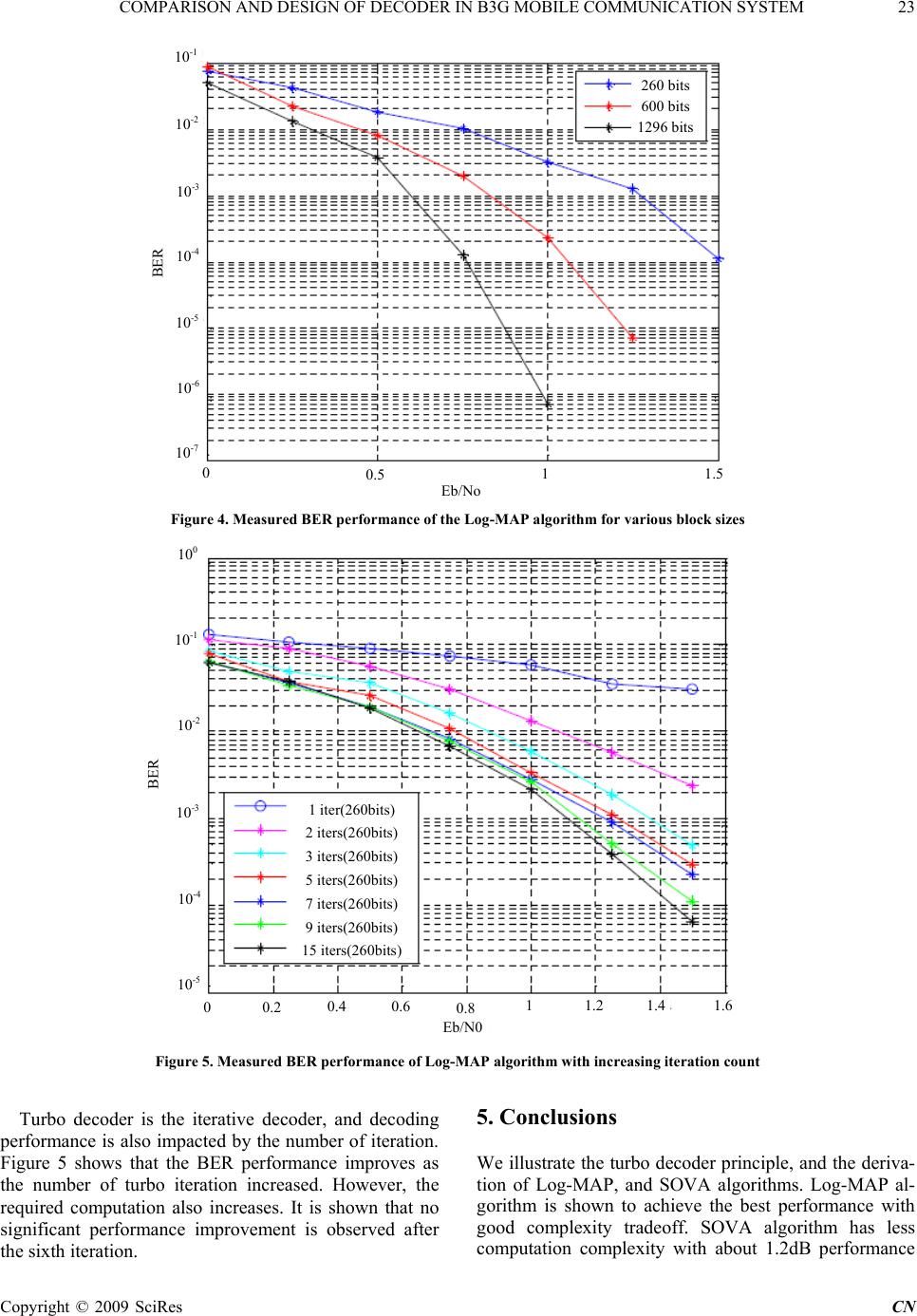

COMPARISON AND DESIGN OF DECODER IN B3G MOBILE COMMUNICATION SYSTEM 23
10-1
260 bits
600 bits
1296 bits
10-2
10-3
BER
10-4
10-5
10-6
10-7
0 1.5
1 0.5
Eb/No
Figure 4. Measured BER performance of the Log-MAP algorithm for various block sizes
100
10-1
10-2
BER
1 iter(260bits)
2 iters(260bits)
3 iters(260bits)
5 iters(260bits)
7 iters(260bits)
10-3
10-4
9 iters(260bits)
15 iters
(
260bits
)
10-5
1.4 1.2
11.6 0.4 0.6
0.2 0 0.8
Eb/N0
Figure 5. Measured BER performance of Log-MAP algorithm with increasing iteration count
Turbo decoder is the iterative decoder, and decoding
performance is also impacted by the number of iteration.
Figure 5 shows that the BER performance improves as
the number of turbo iteration increased. However, the
required computation also increases. It is shown that no
significant performance improvement is observed after
the sixth iteration.
5. Conclusions
We illustrate the turbo decoder principle, and the deriva-
tion of Log-MAP, and SOVA algorithms. Log-MAP al-
gorithm is shown to achieve the best performance with
good complexity tradeoff. SOVA algorithm has less
computation complexity with about 1.2dB performance
C opyright © 2009 SciRes CN

24 COMPARISON AND DESIGN OF DECODER IN B3G MOBILE COMMUNICATION SYSTEM
degradation compared with Log-MAP at the BER of 10-2.
We also demonstrate that the performance of turbo code
is directly proportional to the interleaver size and number
of iteration in the turbo decoder. Finally, it is also shown
that the performance is affected by the scale of the input
soft bits power but the effect is negligible when the scal-
ing factor is larger than 0.8.
6. Acknowledgments
The author would like to thank Dr. Li Lu to help to de-
sign simulation platform, and Prof. Gu Xuemai for his
revision of the text, and the editor and the anonymous
reviewers for their contributions that enriched the final
paper.
REFERENCES
[1] PIETROBON S S. Implementation and performance of a turbo/
MAP decoder. Int. J. Satellite Communication, 1998, 16: 23-46.
[2] KAZA J, CHAKRABARTI C. Design and implementation of
low-energy turbo decoders. IEEE Transactions on Very Large
Scale Integration (VLSI) Systems, 2004, 12(9): 968-977.
[3] HAGH M, SALEHI M, ET AL. Implementation issues in turbo
decoding for 3GPP FDD receiver. Wireless Personal Communi-
cations, 2006, 39(2): 165-182.
[4] LEE D-S, PARK I.-C. Low-power log-MAP decoding based on
reduced metric memory access. IEEE Transactions on Circuits and
Systems, 2006, 53(6): 1244-1253.
[5] BOUTILLON E, GROSS W J, GULAK P G. VLSI architectures
for the MAP algorithm. IEEE Transactions on Communications,
2003, 51(2): 175-185.
[6] ANANTHARAM V E Y. Iterative decoder architectures. IEEE
Communications Magazine, 2003, 41(8): 132-140.
[7] KWON T-W, CHOI J-R. Implementation of a two-step SOVA
decoder with a fixed scaling factor. IEICE Transactions on
Communications, E86-B(6): Jun. 2003, 1893-1900.
[8] CHEN Y, PARHI K K. On the performance and imple-
mentation issues of interleaved single parity check turbo product
codes. Journal of VLSI Signal Processing Systems for Signal,
Image, and Video Technology, 2005, 39(1): 35-47.