Int. J. Communications, Network and System Sciences, 2011, 4, 452-455
doi:10.4236/ijcns.2011.47054 Published Online July 2011 (http://www.SciRP.org/journal/ijcns)
Chaotic Encryption Scheme Using 1-D Chaotic Map
Mina Mishra, Vijay H. Mankar
Department of Electronics & Telecommunication, Nagpur University, Maharastra, India
Department of Electronics Engineering, Government Polytechnic Nagpur, Maharastra, India
Received February 5, 2011; revised April 3, 2011; accepted May 14, 2011
Abstract
This paper proposes three different chaotic encryption methods using 1-D chaotic map known as Logistic
map named as Logistic, NLFSR and Modified NLFSR according to the name of chaotic map and non-linear
function involved in the scheme. The designed schemes have been crypt analyzed for five different methods
for testing its strength. Cryptanalysis has been performed for various texts using various keys selected from
domain of key space. Logistic and NLFSR methods are found to resist known plaintext attack for available
first two characters of plaintext. Plaintext sensitivity of both methods is within small range along with me-
dium key sensitivity. Identifiability for keys of first two of the scheme has not been derived concluding that
methods may prove to be weak against brute-force attack. In the last modified scheme avalanche effect found
to be improved compared to the previous ones and method is found to resist brute-force attack as it derives
the conclusion for identifiability.
Keywords: Cryptanalysis, Plaintext Sensitivity, Key Sensitivity, Identifiability, Brute-Force Attack
1. Introduction
Chaotic cryptography [1] deals with hiding and recover-
ing of secret messages using algorithm which consists of
encryption rule that uses chaotic functions (analog or di-
gital). Logistic map is one-dimensio nal map that consists
of a parameter which is acting as secret key in the de-
signed encryption schemes. The proposed methods use
non-linear functions like, sinusoidal, non-linear shift re-
gister and logistic map to built confusion and diffusion.
The sine function describes a smooth repetitive oscil-
lation. It’s most basic form as a function of time (t) is:



sinyt At

 
where, A, the amplitude is th e pe ak deviation of th e func-
tion from its center position. ω, the angular frequency,
specifies how many oscillations occur in a unit time in-
terval, in radians per second. φ, the phase, specifies
where in its cycle the oscillation begins at t = 0.
A NLFSR (Non-Linear Feedback Shift-register) is a
common component in modern stream ciphers, especially
in RFID and smartcard applications. NLFSRs are known
to be more resistant to cryptanalytic attacks than Linear
Feedback Shift Registers (LFSR’s), although construction
of large NLFSRs with guaranteed long periods remains
an open problem. A NLFSR, is a shift register whose cu-
rrent state is a non-linear function of its previous state.
The NLFSR used here is shown in Figure 1 output.
The logistic map is a polynomial mapping of degree 2,
it takes a point, in a plane and maps it to a new point
using followi n g exp ressions:

 
11
x
krxk xk ;
where, map depends on the parameter r. From r = 3.57 to
r = 4, the map exhibits chaotic behavior which is shown
in Figure 2.
Cryptanalysis is the study of attacks against crypto-
graphic schemes to disclose its possible weakness. Dur-
ing cryptanalyzing a ciphering algorithm, the general
assumption made is that the cryptanalyst knows exactly
the design and working of the cryptosystem under study,
i.e., he/she knows everything about the cryptosystem ex-
cept the secret key. It is possible to differentiate between
different levels of attacks on cryptosystems. They are
briefly explained as fol l ows:
a) Cipher text-only attack: The attacker possesses a
string of cipher text.
b) Known plain text: The attacker possesses a string of
plain text, p, and the corresponding cipher text, c.
c) Chosen plain text: The attacker has obtained tempo-
rary access to the encryption machinery. He nce he/she can
choose a plain text string, p, and construct the corres-

M. MISHRA ET AL. 453
Figure 1. NLFSR using 8-bit shift registers.
Figure 2. Plot of Logistic map for r = 3.99 , x(0) = 0.99, n = 50 00.
ponding cipher text string, c.
d) Chosen cipher text: The attacker has obtained tem-
porary access to the decryption machinery. Hence he/ she
can choose a cipher text string, c, and construct the corre-
sponding plain text string, p.
e) Brute Force Attack: A brute force attack is the me-
thod of breaking a cipher by trying every possible key.
The brute force attack is the most expensive one, owing
to the exhaustive search.
In addition to the five general attacks described above,
there are some other specialized attacks, like, differential
and linear attacks.
Differential cryptanalysis is a kind of ch osen-plaintext
attack aimed at finding the secret key in a cipher. It ana-
lyzes the effect of particular differences in chosen plain-
text pairs on the differences of the resultant cipher text
pairs. These differences can be used to assign probabili-
ties to the possible keys and to locate the most probable
key.
Linear cryptanalysis is a type of known-plaintext at-
tack, whose purpose is to construct a linear approximate
expression of the cipher under study. It is a method of
finding a linear approximation expression or linear path
between plaintext and cipher text bits and then extends it
to the entire algorithm and finally reaches a linear appro-
ximate expression without intermediate value.
2. Methodology
The complete methodology involved during designing is
clearly cited with the help of block diagram as shown in
Figure 3.
The plain text is encrypted by an encryption rule which
uses non-linear function and the state generated by the
chaotic system in the transmitter [2]. Th e scrambled out-
put is inputted further to the chao tic system such that the
chaotic dynamics is changed continuously in a very
complex way. Then another state variable of the chaotic
system [3] in the transmitter is transmitted through the
channel.
Recovery of the plaintext is done by decrypting the
input (ciphertext) using reverse process of en cryption, as
used in the transmitter.
In the modified NLFSR method traditional encryption
method is used along with above method. For Logistic-
sinusoidal function and logistic map and for NLFSR-
Non-linear shift register and logistic map has been used
respectively.
3. Analysis and Results
The analysis accomplished on the designed ciphers has
been done for key space [4], avalance effect, known-
plaintext attack, Identifiability [5,6] and results are cited
in tabular form.
a) Logistic: Key Space range is from 3.57 to 4.0;
b) NLFSR: Key Space range is from 3.57 to 4.0;
c) Modified NLFSR: Key space is from 3.57 to 4.0.
4. Conclusions and Future Scope
Tables 1 and 2 show that Logistic and NLFSR methods
are found to resist known plaintext attack for available
first two characters of plaintext but modified NLFSR
proves its resistance against the attack for available some
numbers of characters of plaintext as given in the column
of Table 3. It also proves its resistance against brute-
force attack by deriving conclusion for identifiability of
selected key. All the three methods are similar to one-
time pad type instead more secure.
More secure ciphers can be designed and crypt ana-
lyzed [7,8] using different non-linear functions and 2-D
Figure 3. Methodology used in design of chaotic cryptosys-
tem. (a), Transmitter end (encryptor); (b), Receiver end (de-
cryptor). (p: plaintext; c: ciphertext; x: state of chaotic fun c-
tion; y: Intermediate encrypted plaintext).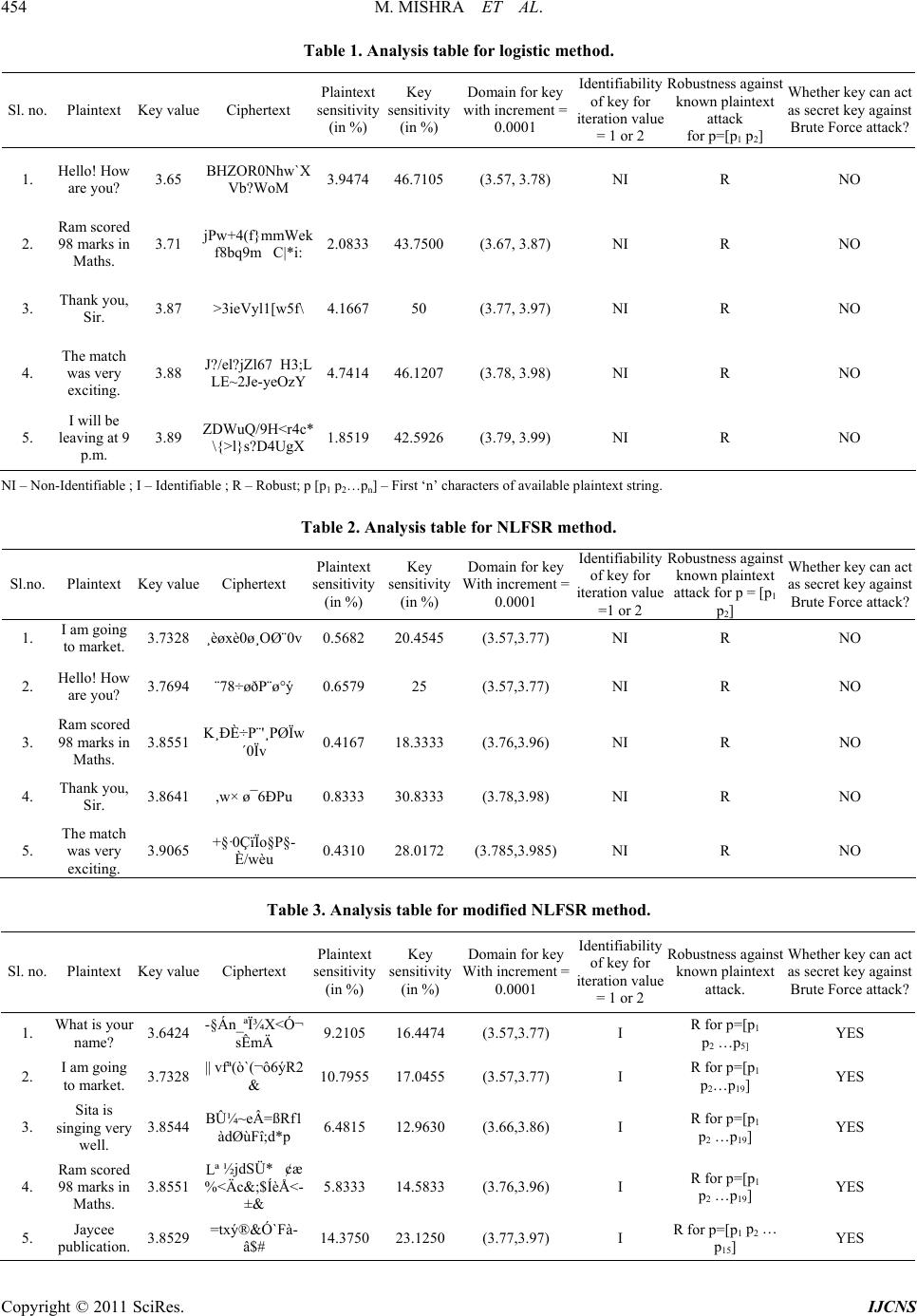

M. MISHRA ET AL. 454
Table 1. Analysis table for logistic method.
Sl. no. Plaintext Key value Ciphertext Plaintext sensitivity
(in %)
Key
sensitivity
(in %)
Domain for key
with increment =
0.0001
Identifiability
of key for
iteration value
= 1 or 2
Ro
b
ustness against
known plaintext
attack
for p=[p1 p2]
Whether key can act
as secret key against
Brute Force attack?
1. Hello! How
are you? 3.65 BHZOR0Nhw`X Vb?WoM 3.947446.7105(3.57, 3.78) NI R NO
2. Ram scored
98 marks in
Maths. 3.71 jPw+4(f}mmWek
 f8bq9mC|*i: 2.083343.7500(3.67, 3.87) NI R NO
3. Thank you,
Sir. 3.87 >3ieVyl1[w5f\ 4.166750 (3.77, 3.97) NI R NO
4. The match
was very
exciting. 3.88 J?/el?jZl67 H3;L
LE~2Je-yeOzY 4.741446.1207(3.78, 3.98) NI R NO
5. I will be
leaving at 9
p.m. 3.89 ZDWuQ/9H<r4c*
\{>l}s?D4UgX 1.851942.5926(3.79, 3.99) NI R NO
NI – Non-Identifiable ; I – Identifi able ; R – Robust; p [p1 p2…pn] – First ‘n’ characters of available plaintext string.
Table 2. Analysis table for NLFSR method.
Sl.no. Plaintext Key value Ciphertext Plaintext sensitivity
(in %)
Key
sensitivity
(in %)
Domain for key
With increment =
0.0001
Identifiability
of key for
iteration value
=1 or 2
Robustness against
known plaintext
attack for p = [p1
p2]
Whether key can act
as secret key against
Brute Force attack?
1. I am going
to market. 3.7328 ¸èøxè0ø¸Oب0v 0.5682 20.4545(3.57,3.77) NI R NO
2. Hello! How
are you? 3.7694 ¨78÷øðP¨ø°ý 0.6579 25 (3.57,3.77) NI R NO
3. Ram scored 98 marks in
Maths. 3.8551 K¸ÐÈ÷P¨'¸PØÏw
´0Ïv 0.4167 18.3333(3.76,3.96) NI R NO
4. Thank you,
Sir. 3.8641 ,w× ø¯6ÐPu 0.8333 30.8333(3.78,3.98) NI R NO
5. The match was very
exciting. 3.9065 +§·0ÇïÏo§P§-
È/wèu 0.4310 28.0172(3.785,3.985) NI R NO
Table 3. Analysis table for modified NLFSR method.
Sl. no. Plaintext Key value Ciphertext Plaintext sensitivity
(in %)
Key
sensitivity
(in %)
Domain for key
With increment =
0.0001
Identifiability
of key for
iteration value
= 1 or 2
Robustness against
known plaintext
attack.
Whether key can act
as secret key against
Brute Force attack?
1. What is your
name? 3.6424 -§Án_ªÏ¾X<Ó¬ sÊmÄ 9.2105 16.4474(3.57,3.77) I R for p=[p1
p2 …p5] YES
2. I am going
to market. 3.7328 || vfª( ò `(¬ô6ýR2 & 10.795517.0455(3.57,3.77) I R for p=[p1
p2…p19] YES
3. Sita is singing very
well. 3.8544 BÛ¼~eÂ=ßRf1
àdØùFî;d*p 6.4815 12.9630(3.66,3.86) I R for p=[p1
p2 …p19] YES
4. Ram scored 98 marks in
Maths. 3.8551 Lª 
½jdSÜ* ¢æ
%<Äc&;$ÍèÅ<-
±& 5.8333 14.5833(3.76,3.96) I R for p=[p1
p2 …p19] YES
5. Jaycee
publication. 3.8529 =txý®&Ó`Fà- â$# 14.375023.1250(3.77,3.97) I
R for p=[p1 p2 …
p15] YES

M. MISHRA ET AL. 455
chaotic maps [9] using different encryption rule. Im-
provement in the property of avalanche effect of designed
ciphers is required in future.
5. References
[1] F. Dachselt and W. Schwarz, “Chaos and Cryptography,”
IEEE Transactions on Circuits and Systems I, Vol. 48,
No. 6, 2001, pp. 1498-1509.
doi:10.1109/TCSI.2001.972857
[2] T. Yang, “A Survey of Chaotic Secure Communication
Systems,” International Journal of Computational Cog-
nition, Vol. 2, No. 2, 2004, pp. 3473-3749.
[3] G. Alvarez, F. Montoya, M. Romera and G. Pastor, “Cha-
otic Cryptosystems”, In: L. D. Sanson, Ed., Proceedings
of the IEEE 33rd 1999 Annual International Carnahan
Conference on Security Technology, Madrid, 5-7 October
1999, pp. 332-338.
[4] G. Alvarez and S. Li, “Some Basic Cryptographic Re-
quirements for Chaos-Based Cryptosystems,” Interna-
tional Journal of Bifurcation and Chaos, Vol. 16, No. 8,
2006, pp. 2129-2151.
doi:10.1142/S0218127406015970
[5] S. Nõmm and C. H. Moog, “Identifiability of Discrete-
Time Nonlinear Systems,” Proceedings of the 6th IFAC
Symposium on Nonlinear Control Systems, Stuttgart, Vol.
1, No. 3, 2004, pp. 477-489.
[6] F. Anstett, G. Millerioux and G. Bloch, “Chaotic Cryp-
tosystems: Cryptanalysis and Identifiability,” IEEE Tran-
sactions on Circuits and Systems, Vol. 53, No. 12, 2008,
pp. 2673-2680.
[7] E. Solak, “On the Security of a Class of Discrete-Time
Chaotic Cryptosystems,” Physics Letters A, Vol. 320, No.
5-6, 2004, pp. 389-395.
doi:10.1016/j.physleta.2003.11.008
[8] N. Masuda and K. Aihara, “Cryptosystems with Discre-
tized Chaotic Maps,” IEEE Transactions on Circuits and
Systems I, Vol. 53, No. 6, 2002, pp. 1341-1352.
[9] F. Huang and Z. H. Guan, “Cryptosystem Using Chaotic
Keys,” Chaos, Solitons and Fractals, Vol. 23, No. 3, 2005,
pp. 851-855.doi:10.1016/j.chaos.2004.05.026