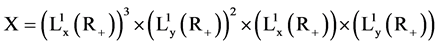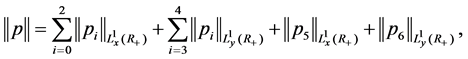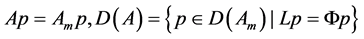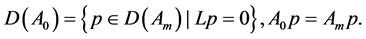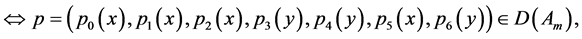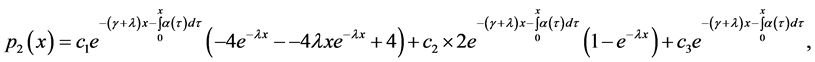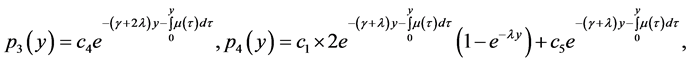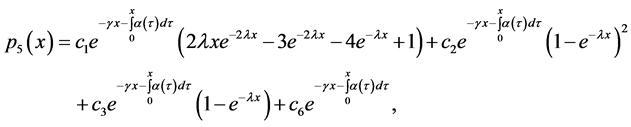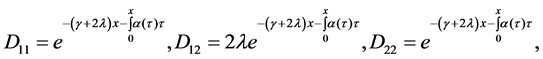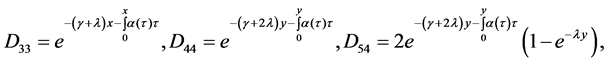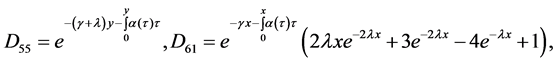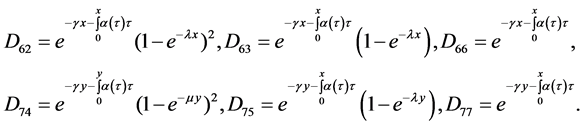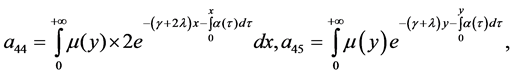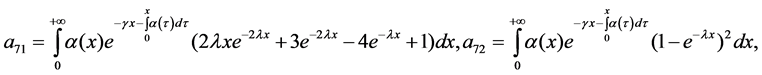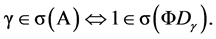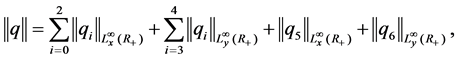Received 5 May 2015; accepted 23 June 2015; published 30 June 2015

ABSTRACT

We investigate Gaver’s parallel system attended by a cold standby unit and a repairman with multiple vacations. By using C₀-semigroup theory of linear operators in the functional analysis, we prove well-posedness and the existence of the unique positive dynamic solution of the system.

Keywords:

Gaver’s Parallel Pystem, C₀-Semigroup, Well-Posedness

1. Introduction

The study of repairable systems is an important topic in reliability. The Gaver’s Parallel system is one of the classical repairable systems in reliability. Since the strong practical background of The Gaver’s parallel system, many researchers have studied them extensively under varying assumptions on the failures and repairs, see [1]-[3]. The repairman leaves for a vacation or does other work when there are no failed units for repair in system, which can have important influence to performance of system. In [4], the authors studied Gaver’s parallel system attended by a cold standby unit and a repairman with multiple vacations and obtained some reliability expressions such as the Laplace transform of the reliability, the mean time to the first failure, the availability and the failure frequency of the system. In [4], the authors used the dynamic solution in calculating the availability and the reliability. But they did not discuss the well-posedness and the existence of the positive dynamic solution. Motivated by this, we study in this paper the well-posedness and the existence of a unique positive dynamic solution of the system, by using 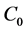-semigroup theory of linear operators. For background reading on semigroup theory we refer to [5] or [6]. First we formulate the model of the system as an abstract Cauchy problem in a Banach space, next we show that the system operator generates a positive contraction -semigroup, and finally we prove that the system is well-posed and there is a unique positive dynamic solution.

The Gaver’s parallel system attended by a cold standby unit and a repairman with multiple vacations can be described by the following equations (see [4]).

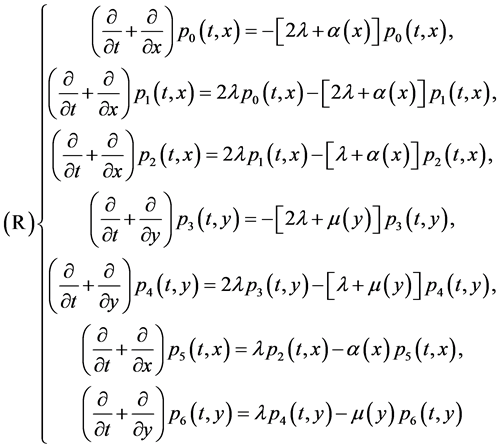
with the boundary conditions

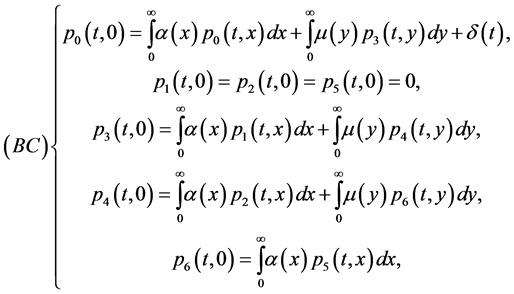
And the initial conditions

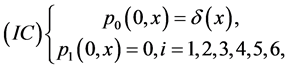where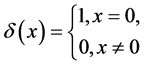

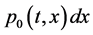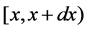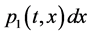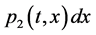Here; gives the probability that at time t two units are operating, one unit is under standby, the repairman is in vacation, the system is good and the elapsed repair time lies in; represents the probability that at time two units are operating, one unit is waiting for repair, the repairman is in vacation, the system is good and the elapsed repair time lies in; represents the probability that at time two unit is operating, one unit is waiting for repair, the repairman is in vacation, the system is good and the elapsed repair time lies in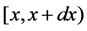; 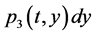represents the probability that at time two units are operating, one unit being repaired, the system is good and the hours that the failed unit has been repaired lies in; represents the probability that at time one unit is operating, one unit being repaired, one unit is waiting for repair, the system is good and the hours that the failed unit has been repaired lies in; represents the probability that at time three units are waiting for repair, the repairman is in vacation, the system is down and the elapsed repair time lies in; represents the probability that at time one unit being repaired, two unit is waiting for repair, the system is down and the hours that the failed unit has been repaired lies in; are positive constants; is the vacation rate function; is the repair rate function.

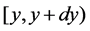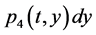
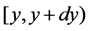
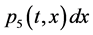
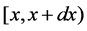
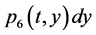
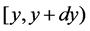
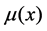
Throughout the paper we require the following assumption for the vacation rate function and the repair rate function.

General Assumption 1.1: The functions and are measurable and bounded such that

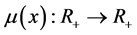
2. Problem as an Abstract Cauchy Problem

To apply semigroup theory we transform in this section the system, , into an abstract Cauchy problem [5, Def.II.6.1] on the Banach space, where

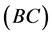
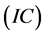
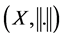
and

.

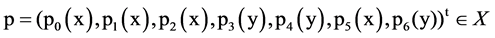
To define the system operator 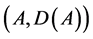we introduce a “maximal operator” on X given as

where

To model the boundary conditions (BC) we use an abstract approach as in [7]. For this purpose we consider the “boundary space” 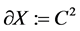and then define “boundary operators” and as follows.

and

,

where

,

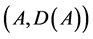
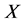
The system operator on is then defined as

With these definitions the above equations (R), (BC) and (IC) are equivalent to the abstract Cauchy problem

(ACP)

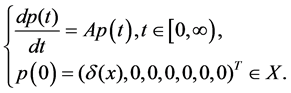
3. Characteristic Equation

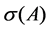
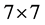
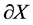
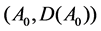
In this section we characterize by the spectrum of a scalar -matrix, i.e., or we obtain a characteristic equation which relates to the spectrum of an operator on the boundary space. For this purpose, we apply techniques and results from [7]. We start from the operator defined by

The elements in can be expressed as follows.

Lemma 3.1: For, we have

(1)

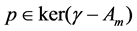
Using [8, Lemma 1.2], the domain of the maximal operator decomposes as

.

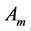
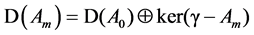
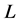
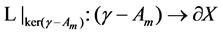
Moreover, since is surjective, is invertible for each, see [8, Lemma 1.2]. We denote its inverse by

and call it “Dirichlet operator”.

We can give the explicit form of as follows.

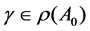
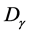
Lemma 3.2: For each, the operator has the form

,

where

For, the operator can be represented by the -matrix

,

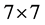
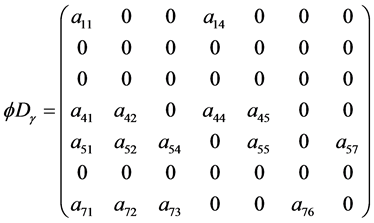
where

The Following result, which can be found in [9], plays important role for us to prove the well-posedness of the system.

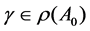
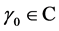
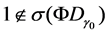
Lemma 3.3 (The characteristic equation): If and there exists such that, then

4. Well-Posedness of the System

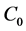
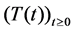
Our main goal in this section is to prove the well-posedness and the existence of a unique positive dynamic solution of the system. We first prove that the operator A generates a positive contraction -semigroup. For this purpose we will check that operator A fulfills all the conditions in the Phillips’ theorem, see [6, Thm. C-II 1.2]. The following lemma shows the surjectivity of for.

Lemma 4.1: If, , then.

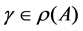
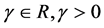
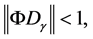
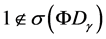
Proof: Let. Then all the entries of are positive and using only elementary calculations one can show that both column sums are strictly less than 1. Hence, and thus. Using Lemma 3.3 we conclude that.

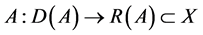
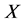
Lemma 4.2: is a closed linear operator and is dense in.

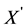
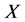
If denotes the dual space of, then.

It is obvious that 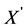is a Banach space endowed with the norm

where.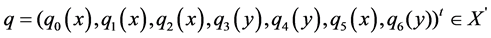

Lemma 4.3: The operator 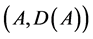is dispersive.

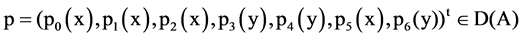
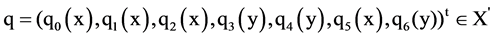
Proof: For, we define

,

where 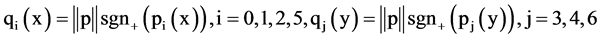and

Noting the boundary condition, it is not difficult to see that. By [6] (p. 49) we obtain that is a dispersive operator.

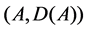
From Lemma 4.1 - 4.3 we see that all the conditions in Phillips’ theorem (see [6], Thm. C-II 1.2]) are fulfilled and thus we obtain the following result.

Theorem 4.4: The operator generates a positive contraction -semigroup.

From Theorem 4.4 and [5] (Cor.II.6.9) we can characterize the well-posedness of 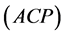as follows.

Theorem 4.5: The associated abstract Cauchy problem is well-posed.

From Theorem 4.5 and [5] (Prop.II.6.2) we can state our main result.

Theorem 4.6: The system and has a unique positive dynamic solution

.

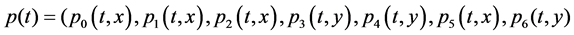
Acknowledgment

This work was supported by the National Natural Science Foundation of China (No.11361057).

Cite this paper

Abdukerim Haji,Bilikiz Yunus, (2015) Well-Posedness of Gaver’s Parallel System Attended by a Cold Standby Unit and a Repairman with Multiple Vacations. Journal of Applied Mathematics and Physics,03,821-827. doi: 10.4236/jamp.2015.37101

References