Received 1 April 2015; accepted 23 June 2015; published 30 June 2015

ABSTRACT

Fuzzy C-means (FCM) is simple and widely used for complex data pattern recognition and image analyses. However, selecting an appropriate fuzzifier (m) is crucial in identifying an optimal number of patterns and achieving higher clustering accuracy, which few studies have investigated. Built upon two existing methods on selecting fuzzifier, we developed an integrated fuzzifier evaluation and selection algorithm and tested it using real datasets. Our findings indicate that the consistent optimal number of clusters can be learnt from testing different fuzzifiers for each dataset and the fuzzifier with the lowest value for this consistency should be selected for clustering. Our evaluation also shows that the fuzzifier impacts the clustering accuracy. For longitudinal data with missing values, m = 2 could be an empirical rule to start fuzzy clustering, and the best clustering accuracy was achieved for tested data, especially using our multiple-imputation based fuzzy clustering.

Keywords:

Fuzzifier, Fuzzy C-Means, Multiple Imputation-Based Fuzzy Clustering (MIFuzzy), Missing Data, Longitudinal Data

1. Introduction

Fuzzy C-means (FCM) is an efficient clustering method in analyzing complex data patterns. FCM introduces the concept of membership into data partition, and uses the levels of membership to indicate the degree to which an object belongs to different clusters. In various applications and for complex data, FCM demonstrates its robustness and better data partition than crisp clustering such as in MRI image studies [1]-[4]. Recently, one major FCM variant, Multiple Imputation-based Fuzzy clustering (MIFuzzy) has been developed to detect patterns and help causal inference in health and biomedical studies [5] [6].

The fuzzifier, m, also called weighting exponent, ranges from 1 to +∞. When m is close to one, the FCM approaches the hard c-means algorithm; while m approaches infinity, FCM searches the mass center of the data. Proper selection of fuzzifiers can suppress noises and improve the smoothness of FCM membership function. A smaller fuzzifier usually achieves better computational performance. The existing FCM algorithms typically set the fuzzifier to 2, which is an empirical rule but without much evidence. There are also some FCM-centric methods [7]-[11] for selecting fuzzifiers based on FCM optimization, e.g., where n is the sample size [7]. Recently, two data-centric methods [12] [13] were proposed to establish the relationship between the fuzzifier and the characteristics of datasets. Specifically, these studies examined the influence of dominant data features (e.g., dimension and sample size) on selecting fuzzifiers.

To select appropriate fuzzifiers and achieve better clustering accuracy, this paper proposes a new integrated framework for fuzzifier-selection. Our computational results show that the consistent optimal number of clusters can be learnt from testing different fuzzifiers for each dataset; and the fuzzifier with the lowest value for this consistency should be selected for clustering. Furthermore, we evaluated the impact of fuzzifier on cluster accuracy. Specifically, we tested FCM on 3 real datasets with different fuzzifier values (MIFuzzy was used for datasets with missing values), and used 2 typical validation indices (i.e., VSC, XB) for fuzzy clustering to evaluate the consistency of the optimum number of clusters with different m.

The remainder of this paper is organized as follows. Section 2 introduces two existing fuzzifier computing methods. Section 3 demonstrates our integrated fuzzifier evaluation and selection algorithm. Section 4 concludes our work.

2. Two Fuzzifier Computing Methods

References [12] [13] used different methods to obtain fuzzifier directly from datasets. Reference [12] theoretically proved and computed the fuzzifier in the process of FCM clustering by searching a global optimal solution. Assuming the fuzzifier m, the number of data point n, and the dimension s, they designed two different rules to compute fuzzifier as follows:

where, and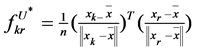, where k and r denote the index of different data. denotes the maximum eigenvalue of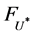. Rule is an approximation of Rule, indicating the

fuzzifier is related to the data dimension. According to Reference [12], if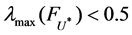, the fuzzifier can be directly computed with Rule, otherwise Rule and Rule 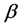are invalid.

Similarly, Reference [13] agrees that the fuzzifier m is related to the dataset dimension and size. Differently, they first used the probability theory to analyze the probability of a well-defined cluster. They found that the probability of a well-defined cluster exponentially decreases with respect to the dimension of dataset, and slightly slower with the increasing sample size. They argued that the fuzzifier m should at least qualitatively follow this tendency. They learnt a general functional relation between the fuzzifier and the dataset properties (data dimension and sample size) as shown in Equation (1) by studying the correlation among m, s, and n based on a comprehensive simulation.

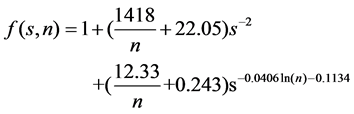(1)

where s also denotes the dimension of dataset, and n describes the sample size.

3. A New Integrated Fuzzifier Evaluation and Selection (NIFEs) Algorithm

This section describes and demonstrates our new integrated fuzzifier evaluation and selection (NIFEs) algorithm.

3.1. Conceptual Framework for NIFEs Algorithm

Our conceptual framework for NIFEs algorithm is shown in Figure 1. Specifically, we use typical fuzzy clustering validation indices to evaluate the consistency in choosing the optimal number of clusters for a range of fuzzifiers; and then analyze the impact of fuzzifiers on clustering accuracy. We used two major validation indexes for fuzzy clustering: widely-used XB [14], and recently-developed VSC [15] for datasets with overlapped clusters. XB is directly related to the fuzzifier while VSC is unrelated to the fuzzifier.

Moreover, we used 3 real datasets to evaluate our algorithm as shown in Table 1: IRIS [16], Infectious Disease (ID) and TDTA [17]. Briefly, IRIS consists 150 samples from three species: Setosa, Virginica and Versicolor. Length and width of the sepals and petals (i.e., four attributes) were measured for each species. ID includes a pediatric cohort of 162 infants with 7 anti-measles antibody measures each from 2 to 8 months before vaccination. TDTA data were collected from a culturally-adapted smoking cessation intervention for Asian Americans with 9 intervention attributes. In particular, we used the classical FCM for IRIS; as ID and TDTA are longitudinal data with missing values, we used MIFuzzy [5] as mentioned in Section 1.

3.2. Demonstrating New Integrated Fuzzifier Evaluation and Selection (NIFEs) Algorithm

The main idea of our new integrated fuzzifier selection (NIFEs) algorithm is to select a proper fuzzifier to ensure the optimal cluster identification and accuracy. Specifically, given the initial fuzzifier range as M: , and the validation index set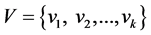, we implement fuzzy clustering algorithms (e.g., FCM, MIFuzzy) with given M, and obtain the validation index set V to evaluate the clustering results. For each validation index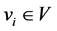, we use 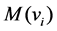to denote the set of available fuzzifiers that can identify the optimum number of clusters. By default, we set. Then, we select as the final fuzzifier. The NIFEs pseudo codes are displayed in Figure 2. Here, we set v₁= XB and v2 = VSC as examples to demonstrate our NIFEs algorithm. Define the XB peak as that satisfies and, where j denotes the cluster number. Then, the optimal number of clusters is.

FCM was performed on IRIS while MIFuzzy on ID and TDTA with a range of m (m_low = 2; m_max = 4). The variation of validation indices (v₁ = XB and v₂ = VSC) was obtained as shown in Figure 3. Then we examined if

these validation indices can consistently point to an optimal number of clusters with the range of fuzzifiers.

The optimal cluster number is corresponding to the smallest values of v₁= XB or v₂ = VSC. As mentioned above, XB is fuzzifier-related, incorporating the compactness and separation measures of clusters. As demonstrated in the three datasets, shown in Figure 3(a) IRIS, Figure 3(b) TDTA, and Figure 3(c) ID, the overall trends of XB are consistent across different fuzzifiers m, which implies that as long as XB can point to an optimal number of clusters, the smallest m could be identified. XB has consistent local minimum at 2 clusters with. For the longitudinal datasets ID and TDTA using MIFuzzy, XB achieves the consistent local minimum with.

Furthermore, we examined the variation of VSC, a non-fuzzifier-related index, over the same datasets, shown in Figures 3(d)-(f). The VSC curve of m = 2 is corresponding to the lower red curve. VSC incorporates the compactness and overlap measures to evaluate the quality of FCM. For all three datasets, VSC identifies the optimal number of clusters with a consistent minimum value across different fuzzifers.

Since we can obtain the consistency of an optimal number of clusters by testing different fuzzifiers, the fuzzfier with the lowest value for this consistency is regarded as the most appropriate for fuzzy clustering because of computational efficiency. Note that our idea is to detect this important consistency to establish a generalized fuzzifier evaluation algorithm; determining a final number of optimal clusters is not the scope of this study but a natural next step. Table 2 shows the fuzzifier obtained with NIFEs over these 3 datasets.

Using the two methods from References [12] and [13], we compute the optimal fuzzifiers for all these datasets as our baseline. Table 3 displays the m values for each dataset from these two methods. Particularly, inf in Table 3 means that the Reference [12] method failed. Compared to Table 3, NIFES agrees with the majority of fuzzifier identified by Reference [12] or [13]. In general, NIFEs seems to be more reliable, for example, m = 2 is appropriate for IRIS according to literature but Reference [13] suggested m = 4; for TDTA, both Reference [13] and our NIFES agree m = 2, which is appropriate according to our previous investigation while Reference [12] suggested 3.993.

Furthermore, given the real cluster number for each data set shown in Table 1, we examined the clustering accuracy of different m displayed in Figure 4. Given a sample size N, denote G as the correct number of cases identified in known clusters, the clustering accuracy is defined as G/N.

As shown in Figure 4, fuzzifier m = 2 could lead to better or comparable clustering accuracy given the identified optimal cluster number across the three datasets. Especially for longitudinal data with missing values (TDTA and ID), m = 2 shows the correct accuracy according to our known results.

4. Conclusions

This paper investigates selection of fuzzifier, an important element for FCM, using three real datasets: one well-

known biological data, IRIS; and two longitudinal data with missing values, TDTA and ID. We design a new integrated fuzzifier evaluation and selection (NIFEs) algorithm to assess and select the proper fuzzifer. The conceptual NIFEs framework is comprehensive, involving testing (non-)fuzzier related indices and clustering accuracy across a range of fuzzifiers. Our results indicate that our NIFEs algorithm is more reliable than two existing methods and could be a complementary reference for the fuzzy clustering field. Our findings indicate that the consistent optimal number of clusters can be learnt from testing different fuzzifiers for each dataset and the fuzzifier with the lowest value for this consistency should be selected for clustering for computational efficiency. Our evaluation also shows that the fuzzifier impacts the clustering accuracy. For longitudinal data with missing values, m = 2 could be an empirical rule to start fuzzy clustering, and the best clustering accuracy was achieved for tested data, especially using our multiple-imputation based fuzzy clustering.

Acknowledgements

This research was supported by NIH grant R01 DA033323-01A1, 1UL1RR031982-01 Pilot Project to Dr. Fang.

Cite this paper

Chanpaul Jin Wang,Hua Fang,Sun Kim,Ann Moormann,Honggang Wang, (2015) A New Integrated Fuzzifier Evaluation and Selection (NIFEs) Algorithm for Fuzzy Clustering. Journal of Applied Mathematics and Physics,03,802-807. doi: 10.4236/jamp.2015.37098

References

NOTES

^*Corresponding author.