Received 3 March 2015; accepted 23 June 2015; published 30 June 2015

ABSTRACT

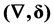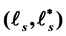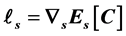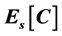As stochastic gradient and Skorohod integral operators, is an adjoint pair of unbounded operators on Guichardet Spaces. In this paper, we define an adjoint pair of operator, where with being the conditional expectation operator. We show that 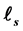(resp.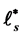) is essentially a kind of localization of the stochastic gradient operators (resp. Skorohod integral operators ). We examine that and 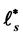satisfy a local CAR (canonical ani-communi- cation relation) and forms a mutually orthogonal operator sequence although each 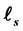is not a projection operator. We find that 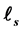is s-adapted operator if and only if 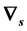is s-adapted operator. Finally we show application exponential vector formulation of QS calculus.

Keywords:

Stochastic Gradient Operator, Skorohod Integral Operator, Localization, Ex-Ponential Vector, Guichardet Spaces

1. Introduction

The quantum stochastic calculus [4] [6] developed by Hudson and Parthasarathy is essentially a noncommutative extension of classical Ito stochastic calculus. In this theory, annihilation, creation, and number operator processes in boson Fock space play the role of “quantum noises”, [2] which are in continuous time. On the other hand, the quantum stochastic calculus has been extended by Hitsuda is by means of the Hitsuda-Skorohod integral of anticipative process [3] [9] and the related gradient operator of Malliavin calculus. In this noncausal formulation the action of each QS integral is defined explicitly on Fock space vectors, and the essential quantum Ito formula is seen in terms of the Skorohod isometry.

In 2002, Attal [1] unify and extend both of the above approaches on Guichardet spaces. In this note, explicitly definitions of QS integrals provided and introduced no unnatural domain limitations. Moreover, maximality of operator domains is demon-strated for these QS integrals on Guichardet spaces.

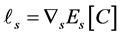In this argument, we define an adjoint pair of operator, where with 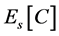being the conditional expectation (operator). The motivation for this study comes from the following observations. It is known that 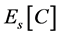is a projection operator on Guichardet Spaces. Hence, restricted to the range of, coincides with the stochastic gradient operator. We show that (resp.) is essentially a kind of localization of the stochastic gradient operators (resp. Skorohod integral operators). We examine that and can be called a local stochastic gradient operators (resp. local Skorohod integral operators). Then, it is necessary and important to study a pair of operator.

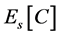This paper is organized as follows. In Section 2, we fix some necessary notations and recall main notions and facts about unbounded operators on Guichardet spaces. In Section 3, Section 4 and Section 5, we state our main results. We first examined that and satisfy a local CAR (canonical anti-communication relation) and forms a mutually orthogonal operator sequence although each’s is not a projection operator. We find that is s-adapted operator if and only if is s-adapted operator. Finally we show application exponential vector formulation of QS calculus.

2. Unbounded Operators on Guichardet Spaces

In this section, we fix some necessary notations and recall main notions and facts about unbounded operators on Guichardet spaces. For detail formulation of unbounded operators, we refer reader to [1].

Let be the set of all nonnegative real numbers and the finite power set of, namely

where denotes the cardinality of as a set, with denoting the collection of element subsets. Obviously,. Particularly, let be an atom of measure 1. We denote by the usual space of square integral real-valued functions on.

Fixing a complex separable Hilbert space, Guichardet space tensor product, which we identify with the space of square-integrable functions, and is denoted by. Guichardet space enjoys a continuous tensor product structure: for each the map

where,.

For a Hilbert space-valued map, let be the map given by

when, we call is Skorohod integrable, is Skorohod integral operator on and

For a map, let and be the maps given by

when, we call and the stochastic gradient of f and the adapted gradient of, respectively. Moreover,

where. Obviously, if, , where.

Let, the adapted projection on is the orthogonal projection onto the closed subspace:

Remark 2.1 As Hilbert space operators, and are unbounded operators. and are closed, densely defined operators. Especially, is adjoint operator of and

where is the number operator, with maximal domain and is identical operator.

Lemma 2.1 [1] Let and be Skorohod integrable, if the map

is integrable, then

. (1)

Lemma 2.2 [1] Let be measurable. If for almost every, then

, (2)

where (1) may call the canonical-commutation relations.

3. Local Skorohod Integral and Stochastic Gradient Operators

In the present section we state and prove our main results. We first make some preparations.

Let be an operator on with domain, we define an conditioned expectation operator on by the a.e. prescription

,

with domain

where, ,.

Clearly, is a subspce of, and for any, we have for a.a.. Thus is an s-adapted subspace.

Remark 3.1 If is s-adapted(i.e. for all, for a.a.), then the subspaces and coincide, and for in this subspace, it follows that

Whenever belongs to. If is densely defined, s-adapted and is closable, then.

Remark 3.2 is s-adapted operator and.

Definition 3.1 For, we call the local stochastic gradient operator and its adjoint operator is the local Skorohod integral operator. And operator domain of is given by

where is operator on.

We note that for,

hence,. Especially, when, we have.

Theorem 3.1 By lemma2.2, we can get the following relations

(3)

which we may call the local CAR(canonical anti-commutation relations).

Proof we note that

The next theorem shows that is not a projection operator on.

Theorem 3.2, whenever and.

Proof Let with. The following algebraic relations are evident for,

We show that, thus

We note that for with, which means that the is not mutually orthogonal. However, the theorem below shows that the local operator sequence is mutually orthogonal.

Theorem 3.3,whenever and.

Proof Let and. If, then we can show that, from which it follows that

Now, if, then by the result of the first step we have

This completes the proof.

Theorem 3.4 is s-adapted operator if and only if is s-adapted operator.

Proof we know that and is s-adapted operator. we have

for a.a., obviously, if is s-adapted, then and for a.a.. On the other hand, if is s-adapted, is also s-adapted.

4. Application to Exponential Vector Formulation of QS Calculus

Recall that in the exponential vector formulation of QS calculus, all processes are defined on a domain of the algebraic tensor product form, where is a dense subspace of and

which is a subset of and denotes the expential vector of the test function which in Guichardet spaces given by.

For all and a.a., we have

and (4)

since, the domain of the form are s-adapted. Note the a.e. identity

where (5)

Theorem 4.1 be an operator on with domain of the form. Then is s-adapted if and only if, for all and:

(6)

where

Proof By definition of, be an operator on with domain of the form. We note that if is s-adapted, then. Let and, by (4), for a.a.,

and so, for a.a.,

Acknowledgements

The authors are extremely grateful to the referees for their valuable comments and suggestions on improvement of the first version of the present paper. The authors are supported by National Natural Science Foundation of China (Grant No. 11261027 and No. 11461061).

Cite this paper

Jihong Zhang,Caishi Wang,Lina Tian, (2015) Localization of Unbounded Operators on Guichardet Spaces. Journal of Applied Mathematics and Physics,03,792-796. doi: 10.4236/jamp.2015.37096

References