Received 6 May 2015; accepted 23 June 2015; published 30 June 2015

ABSTRACT

Mixing and coherence are fundamental issues at the heart of understanding fluid dynamics and other non-autonomous dynamical systems. Recently the notion of coherence has come to a more rigorous footing, in particular, within the studies of finite-time nonautonomous dynamical systems. Here we recall “shape coherent sets” which is proven to correspond to slowly evolving curvature, for which tangency of finite time stable foliations (related to a “forward time” perspective) and finite time unstable foliations (related to a “backwards time” perspective) serve a central role. We compare and contrast this perspective to both the variational method of geodesics [17], as well as the coherent pairs perspective [12] from transfer operators.

Keywords:

Shape Coherent Set, Coherent Pairs, Geodesic Transport Barrier, Finite-Time Stable and Unstable Foliations, Implicit Function Theorem, Continuation, Mixing, Transport

1. Introduction

Understanding and describing mixing and transport in two-dimensional fluid flows have been a classic problem in dynamical systems for decades. Here we focus on three theories related to coherence in finite-time nonautonomous dynamical systems: 1) Shape coherent sets [22] where the nonlinear flow itself as considered to be special “shape coherent sets” reveals that the otherwise complicated flow reduces to a simpler transformation, namely rigid body transformations, on the corresponding time and spatial scales; 2) The geodesic theory of transport [17] which initially describes that transport barriers relate to minimally stretching material lines (“Seeking transport barriers as minimally stretching material lines, we obtain that such barriers must be shadowed by minimal geodesics under the Riemannian metric induced by the Cauchy-Green strain tensor.” [17]) and later it was improved to “stationary values of the averaged strain and the averaged shear,” [18]; 3) Coherent pairs [2] [12] [21] viewed by transfer operators in terms of evolving density. See Table 1. Not all methods are coverer here, notably the combination method of Tallapragada and Ross [26] which gives FTLE like quantities directly from transfer operator.

In this paper, we contrast three perspectives of coherence by calculating several objective measures which are a) the evolution of arc length; b) the relative coherence pairing; c) foliation angles; d) change of curvature; e) registration of shapes; and f) the shape coherence factor for sets developed from each of these methods, two of which are respectively shown in Tables 1-3. We show that each of these three perspectives of coherence may keep its advantages on its corresponding measure. According to a geodesic perspective, arc length should vary

slowly. On the other hand, according to the perspective of shape coherent sets, shape should be roughly preserved and the nonlinear flow restricted to that set should appear as a rigid body motion on that scale of time and space. This suggests that arc length may vary, however generally slowly. For coherent pairs, the definition [12] allows perfect overlap of a set and its image, so an extra condition called\robust must be added, which was later clarified in [11] [13] that effectively numerical diffusion was introduced in the stage of estimating the Ulam- Galerkin matrices that reward sets whose boundary curves do not grow dramatically. This suggests an implicit connection between the geodesic theory and the coherent pairs theory. See also [10]. Table 2 and Table 3 summarize a contrast study for benchmark examples, the Rossby wave and the double gyre system, where for the best possible comparison, a specific “coherent set” was found that seems to be roughly the same set as identified by all three perspectives. Therefore, the definition in each is not identical. Furthermore, there are numerical estimation issues that likely vary between each approach, as seen for example especially in the transfer operator method since many cells are required, and therefore many orbit samples for a reasonable estimate of a boundary curve.

It may seem striking that each method performs well on the measures of the other methods. There are of course differences between the methods as well, since each tends to identify sets that the other two do not, with significant difference in the non-corresponding measure. Note that we have used LCSTool [19] which uses closed shearlines, closed null-geodesics of the Green-Lagrange strain tensor, [18] which was pointed out to be for incompressible flows; these are infinitesimally arc length conserving, but not generally. In the appendix, we show a simple example to demonstrate that there exist continuous families of different shapes with the same area and the same arc length.

2. Shape Coherence, Relative Coherence and Geodesic Transport Barrier

For completeness, in brief detail we review the three methods to be compared, with references to the originating literature for greater detail. Let (, ,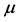) be a measure space, where 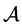is a 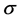-algebra and 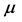is a normalized measure that is not necessarily invariant. We assume that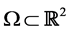. See [12] [21] [22]. Consider the planar nonautonomous differential equation [17],

(1)

We use 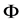to represent the flow map of the system¹.

2.1. Shape Coherence

Here we review shape coherence [22]. We recently introduced a definition concerning coherence called shape coherent sets², motivated by an intuitive idea of sets that “hold together” through finite-time. We connected shape coherent sets to slowly evolving boundary curvature by studying the tangency of finite-time stable and unstable foliations, which relate to forward and backward time perspectives respectively. The zero-angle curves are developed from the nonhyperbolic splitting of stable and unstable foliations by continuation methods that relate to the implicit function theorem. These closed zero-angle curves preserve their shapes in the time- dependent flow by a relatively small change of curvatures. See [22], on calculating the shape coherence factor. Taking a Lagrangian perspective, we offer the following mathematical definition:

Definition 1 [22] Finite Time Shape Coherence The shape coherence factor 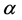between two measurable nonempty sets 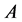and 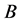under a flow 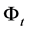after a finite time epoch 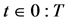is,

(2)

where is a group of transformations of rigid body motions of, specifically translations and rotations descriptive of frame invariance, and for certain problems it may include mirror translations. We interpret to denote Lebesgue measure, but one may substitute other measures as desired. Then we say is finite time shape coherent to with the factor under the flow after the time epoch, but we may say simply that is shape coherent to. We shall call the reference set, and shall be called the dynamic set. In other words, if the flow is restricted to a shape coherent set, then can be considered to be approximately equivalent to a transformation which belongs to the group, rigid body transformations. Throughout this paper we choose to be itself, which means we try to capture those sets with minimal shape change under the flow. Next, we introduce the finite-time stable and unstable foliations which are used to develop the boundaries of the shape coherent sets.

Stated simply, the stable foliation at a point describes the dominant direction of local contraction in forward time, and the unstable foliation describes the dominant direction of contraction in “backward” time. See Figure 1 and Figure 2. They are also called Lyapunov vectors. Generally, the Jacobian matrix, of the flow evaluated at the point has the same action as does any matrix in that a circle maps onto an ellipse. In Figure 1 and Figure 2 we illustrate the general infinitesimal geometry of a small disc of variations from a base point. At, we observe that a circle of such vectors, centered at the point pulls back under to an ellipsoid centered on. The major axis of that infinitesimal ellipsoid defines, the stable foliation at. Likewise, from, a small disc of variations pushes forward under to an ellipsoid, again centered on. The major axis of this ellipsoid defines the unstable foliations,.

To compute the major axis of ellipsoids corresponding to how discs evolve under the action of matrices, we

may refer to the singular value decomposition [14]. Let,

(3)

where denotes the transpose of a matrix, and are orthogonal matrices, and is a diagonal matrix. By convention we choose the index to order,. As part of the standard singular value decomposition theory, principal component analysis provides that the first unit column vector of corresponding to the largest singular value, , is the major axis of the image of a circle under the

matrix around. That is, as seen in Figure 1 describes the vector at that maps onto the major axis, at. Since, and, then recalling the orthogonality of and, it can be shown that, and. Therefore, , and the dominant axis of the image of an infinitesimal circle from comes from,.

We summarize, the stable foliation and unstable foliation at are,

(4)

where is the second right singular vector of, according to Equation (3). And is the first left singular vector of the matrix decomposition, An included angle between a pair of stable and unstable foliations is defined as follows,

Definition 2 [22] The included angle of the finite-time stable and unstable foliations is defined as

(5)

We give a comprehensive discussion of how the non-hyperbolic splitting angle of foliations preserves curvature of a curve in [22], and in turn, slowly changing of curvature yields significant shape coherence as noticed above. In order to generate curves of the zero-splitting angle, we apply the implicit function theorem to induce a continuation theorem, which guarantees that we can use ODE solvers and root-finding methods to describe the curve.

To calculate the shape coherence number is a form of “image registration”, which is the process of transforming different image data into one coordinate system. See [1]-[4]. Image registration is a widely used class of algorithms in the image processing community to solve the following practical problem. Suppose two images (photographs for example) have pieces of the same scene such as a car or a face, then how can the two images be best “aligned” so as to place one figure on top of the other in a manner that emphasizes that the scenes are aligned. By aligned we mean that rotations, and translations may be used, and in the image processing problem often linear scalings as well, but we will not use that class of transformation. In other words, alignment in terms of rigid body motions of two sets is equivalent to the image processing problem of registration, and it is a convenient comparison since image registration is a well matured problem with many fast and accurate algorithms, including methods based on Fourier Transforms, [1] [4]. Since we assume the flow is area- preserving, generally, we use rigid body motions and may include mirror. In Matlab, the command “imregister” is a convenient implementation of image registration. For more details on the algorithm, see [22].

2.2. The Geodesic Theory of LCS

Next, we review the geodesic theory of Lagrangian coherent structures. Consider an evolving material line in the system, which has length

(6)

where denotes the derivative of the flow map, and denotes the Cauchy-Green strain tensor, with refering to the matrix transpose. In [17], a transport barrier of system 1 over the time interval was described as a material curve, whose initial position is a minimizer of the length functional under the boundary conditions,

(7)

(8)

where are the eigenvectors corresponding to the smaller and larger eigenvalues of, is a pointwise normal, smooth perturbation to and are the normalized Lagrangian shear

vector fields, which are defined as, A transport barrier is a hyperbolic

barrier if satisfies the hyperbolic boundary conditions as defined in Equation (7). A transport barrier is a shear barrier if satisfies the shear boundary conditions as defined in Equation (8). For the computational part, for comparison here we use the the “LCS-tools” which were developed by the Nonlinear Dynamical Systems Group at ETH Zurich, led by Prof. George Haller. See. [19].

2.3. The Relatively Coherent Pairs

In this section, we briefly review the coherent pairs. Relatively coherent pairs [21] describe a system by hierar- chical partitions based on the idea of coherent pairs. See [12]. Given the time-dependent flow , through the time epoch of an initial point at time, a coherent pairs can be considered as a pair of subsets of such that,

Definition 3 [12] is a -coherent pair if

(9)

where the pair are ‘robust ’ to small perturbation and

Then we build a relative measure on induced by, where is a nonempty measurable subset of. In this way we enter into refinements of the initial partition on successive scales. A relative measure of to is, [21], for all. From the above definition, it follows that is also a measure space, where is the restriction of to and is a normalized measure on. We call the space, the relative measure space. Now, we define the relatively coherent pairs.

Definition 4 [21] Relatively coherent structures are those -coherent pairs defined in Definition 2.1, with respect to given relative measures on a subset, of a given scale, specializing [12].

To find coherent pairs in time-dependent dynamical systems, we use the Frobenius-Perron operator. If is a nonsingular transformation such that for all satisfying the unique operator defined by,

(10)

for all is called the Frobenius-Perron operator corresponding to S, where. See [2] [20]. Here, can be considered as the flow map and the formula above can be written as

Suppose is a subset of,

and let be a set that includes. We develop partitions for and respectively. In other words, let be a partition for and be a partition for. The Ulam-Galerkin matrix follows a well-known finite-rank approximation of the Frobenius-Perron operator,

where the sequence is a set of test points (passive tracers). See [5]. The computation of coherent pairs is a set-oriented method, but to compare the results to the other two methods which are defined in terms of boundary curves of sets, we must extract boundary curves from the boundaries that are approximated by the set of triangles covering the boundary, [21]. An effective way to extract the boundary is to shrink the size of triangles; then we approximate the boundary by connecting the centers of triangles on these boundary sets, and this is done either by line segments through adjacent triangles, or it could be done with some smoothing by a pair of smoothing splines.

3. Examples

We next apply the three methods to the Rossby wave system and double gyre system, both of which have become classic examples for studying and contrasting coherence and transport, [2] [10] [12] [17] [21].

3.1. The Nonautonomous Double Gyre.

Consider the nonautonomous double gyre system,

(11)

where, , and. See [10] [25]. Let the time interval be. Table 2, Figure 3 and Figure 4 show the numerical results of the comparison among the three theories of the nonautonomous double gyre system.

Consider the example sets shown. Note that the LCS has the smallest arc length change, but the shape coherent sets have the highest shape coherence factor. While the coherent pair number of both the shape coherence derived set and the geodesic transport derived set are shown as 1, since if the image in definition Equation (9) is its image, as the pairing, then 1 will always be the result, but the theory is properly interpreted the entire definition of coherent pairs requires a more careful pairing of sets as discussed above. What is striking here is that three different methods can find comparable sets, as reflected that the measures are similar.On the other hand, not shown here, is that each can find different sets, but the measures between them would ne- cessarily be dramatically different. See Figure 4 for such a scenario where two methods sometimes produce substantially similar regions, but sometimes substantially different regions.

3.2. An Idealized Stratospheric Flow

The second benchmark problem is a quasiperiodic system which represents an idealized zonal stratospheric flow [12] [24]. Consider the following Hamiltonian system where

(12)

Let and the other parameters be the same as stated in [24]. The numerical results in Table 3, Figure 5 and Figure 6 show that the elliptic LCS shown maintains arc length better than the other three curves also in this system, but the coherent pairs have a shape coherence factor a little greater than the first smaller shape coherent sets. Note that although these measurements are so close, that it could be inferred that differences are within the level of numerical accuracy. The degree of coherence becomes rarer for bigger regions, than smaller ones, so we show the second shape coherent sets as a bigger one with the highest shape coherence factor. See Table 3. Again we see each does especially well within its own measures, but quite well across measures. So while each method can and often does develop comparable sets, sometimes they develop dramatically different sets. See Figure 4. It is shown there that the two perspectives often do reveal extremely similar boundaries, but sometimes quite different ones.

4. Conclusions

In this paper, we have reviewed three complementary theories of coherence that come with similar goals but from different perspectives. These are the geodesic theory of LCS which emphasizes stationarity of averaged strain and shear, coherent pairs which describes “very small leakage” of sets and shape coherent sets which emphasizes those sets that preserve their shape by a slowly evolving curvature.

We have then presented two benchmark examples, the double gyre and the Rossby wave, to compare the different methods. In the examples described here, it has been illustrated that all three methods have reasonable and similar numerical results which agree with their own theories, and comparable results between given that similar sets were identified. For arc length, LCS always has the least change; and with respect to shape coherence, the zero-splitting curve has the best shape coherence number; coherent pairs has results very close to them. Notice that here we only compared similar elliptic shapes for all three methods, to allow each the best possibility of doing well relative to each other. On the other hand, each of the three methods can and does find clearly different sets and therefore with significant differences of performance measure. See Figure 7.

We have not found an a priori reason to expect that each of the three definitions of coherence will usually, or even often, find the same sets. A theorem directly connecting them is lacking. Indeed sometimes we find that each finds sets that the others do not, but in such a case, a numerical comparison of the measures included here only points out dramatic differences. Stated in terms of choice, a practitioner may ask which method to use for their own applied problem, but there is no magic bullet or best method to compute coherence. By offering the contrasting perspective of three different concepts of the general idea of coherence, in the same light, we hope that this discussion offers the practitioner a richer mathematical perspective of what is the outcome of what they are computing, no matter what method they choose to use.

Cite this paper

Tian Ma,Erik Bollt, (2015) Contrast of Perspectives of Coherency. Journal of Applied Mathematics and Physics,03,781-791. doi: 10.4236/jamp.2015.37095

References

NOTES

¹The form of may vary, such as, and, because we keep the original forms from different theories for better understanding. However, they represent the same flow.

²In this paper, we always use the initial status of a closed curve as its reference sets, i.e. as in Equation (2).

5BAppendix

Here, we present an example of a continuous two-dimensional family of simply connected sets with the same perimeter, and area, but different shapes. By this observation, we argue that a closed geodesic transport barrier may lose its shape through the flow. Figure 8 shows two simply connect sets, a rectangle with height and width and an annulus sector with angle, inner radius and outer radius. The perimeter

and area of are, and, And the perimeter and area of are, and, Now we assume the two shapes and have the same area and perimeter, so we have the relationships as follows,

(13)

So, for example, let, , and, we have and.