Received 28 April 2015; accepted 23 June 2015; published 30 June 2015

ABSTRACT

In this paper, we consider the direction and stability of time-delay induced Hopf bifurcation in a delayed predator-prey system with harvesting. We show that the positive equilibrium point is asymptotically stable in the absence of time delay, but loses its stability via the Hopf bifurcation when the time delay increases beyond a threshold. Furthermore, using the norm form and the center manifold theory, we investigate the stability and direction of the Hopf bifurcation.

Keywords:

Hopf Bifurcation, Time-Delay, Predator-Prey Model

1. Introduction

Due to its universal existence and importance, the study on the dynamics of predator-prey systems is one of the dominant subjects in ecology and mathematical ecology since Lotka [1] and Volterra [2] proposed the well- known predator-prey model [3]-[6]. Recently, a new method of central manifold has been developed to study the stability of delay induced bifurcation. In this paper, we study the following system:

(1)

with

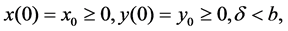(2)

where dot means differentiation with respect to time, 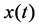and 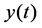are the prey and predator population densities, respectively. Parameter 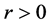is the specific growth rate of prey in the absence of predation and without environment limitation. 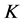is environmental carrying capacity. The functional response of the predator is of Holling’s type with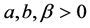. And all parameters involved with the model are positive.

The purpose of this paper is to investigate the effect of time-delay on a modified predator-prey model with harvesting. We discussed the existence of Hopf bifurcation of system (1) and the direction of Hopf bifurcation and the stability of bifurcated periodic solutions are given.

2. Positive Equilibrium and Locally Asymptotically Stabiliy

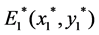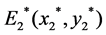After some calculations, we note system (1) has no boundary equilibria. However, it is more interesting to study the dynamical behaviors of the interior equilibrium points and, where

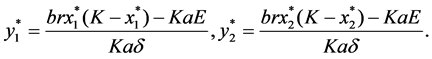
The two distinct interior equilibrium points 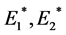exist whenever

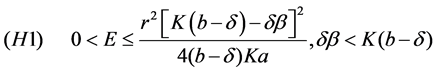
holds.

We transform the interior equilibrium 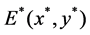to the origin by the transformation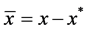,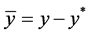. Respectively, we still denote and by and. Thus, system (1) is transformed into

(3)

First, we give the condition such that is locally stable. For simplicity, we denote

(4)

The characteristic polynomial of is

(5)

where

Now we consider the locally asymptotically stabiliy of the system without time-delay. Then we have

(6)

If

holds, then it follows from the Routh-Hurwitz criterion that two roots of (6) have negative real parts.

Theorem 1. If and hold, the interior equilibrium point of system (1) is locally asymptotically stable.

3. Hopf Bifurcaion

In the section, we study whether there exists periodic solutions of system (1) about the interior equilibrium point. Now we have the following results.

Theorem 2. If the system (1) satisfies the hypothesis and holds, then there exists a critical point such that the positive equilibrium point is locally asymptotically stable for and unstable for, where is defined in Equation (14).

By the use of the instability result for the delayed differential Equations, in order to prove the instability of the equilibrium point, it is sufficient to show that there exists a purely imaginary and a positive real such that

(7)

where is defined in Equation (5).

If is a root of Equation (7), then we have

(8)

which leads to

(9)

Let, then Equation (9) takes the form

(10)

Since holds, we have, which leads to. Thus Equation (10) has at least one positive root, which leads to

(11)

Set as the root of Equation (8) with, we have

(12)

where

(13)

Then are a pair of simple purely imaginary roots of Equation (8) with, and we have

(14)

Then by the Butler’s Lemma, is unstable for. On the other hand, if, then Equation (7) have no roots on the imaginary axis. Then Equation (7) for, only has negative real part roots, which implies that is locally asymptotically stable for.

Theorem 3. If the system (1) satisfies the hypothesis and, then the system (1) undergoes Hopf bifurcation at when.

Proof. The Hopf bifurcation will be proved if we can show that

(15)

From Equation (7), we have

(16)

Substituting Equation (8) into Equation (16), we have

(17)

Substituting Equation (14) into the above equation, we have

Therefore, the transversality condition is satisfied. Therefore Hopf bifurcation occurs at.

4. The Direction and Stability of the Hopf Bifurcation

In this section, we analyze the direction and stability of the Hopf bifurcation of (3) obtained in Theorem 3 by taking as the bifurcation parameter.

Let, then is the Hopf bifurcation value of system (3). Rescale the time by to normalize the delay. The periodic solution of system (3) is equivalent to the solution of the following system

(18)

We define as nonnegative integer, define as follows

Rewrite system (18) to

(19)

where

(20)

We use the method which is based on the center manifold and normal form theory, and define. Then the system (19) is transformed into a functional differential equation as

(21)

where and are respectively represented by

(22)

and

(23)

where. By the Riesz representation theorem, there exist a matrix, whose elements are of bounded variation functions such that

(24)

In fact, we can choose

(25)

where is the Dirac delta function. For, we define

(26)

and

(27)

Thus system (21) is equivalent to

(28)

where for.

For, define

(29)

and a bilinear inner product

(30)

where. Then and are adjoint operators. From the discussion in Theorem 2, we know that are eigenvalues of and therefore they are also eigenvalues of.

Suppose is the eigenvector of corresponding to. Thus,. From the definition of we have

Then we have

(31)

Similarly, let be the eigenvector of corresponding to. Then by and the definition of, we obtain

Therefore

(32)

In order to ensure, we need to determine the value of, from Equation (29) we have

(33)

Then we can choose such as

(34)

where is the conjugate complex number of.

Next we will compute the coordinate to describe the center manifold at. Let be the solution of Equation (27) when. Define

(35)

On the center manifold, we have, where

(36)

and are local coordinates for the center manifold in the direction of and. Note that is real if is real. We only concern with the real solutions. For solution of Equation (27), since and Equation (35), we have

(37)

We rewrite above equation as

(38)

where

(39)

From Equation (35) and Equation (36), we obtain that

(40)

Substituting Equation (23) and Equation (40) into Equation (39), we have

(41)

where stands for higher order terms, and

Comparing Equation (39) and Equation (41), we get

(42)

Since depends on and, we need to find the values of and. From Equation (21) and Equation (35), we have

(43)

where

(44)

From Equation (36), we have

(45)

It follows from Equation (39) that

(46)

Comparing the coefficients of and from Equation (45) and Equation (46), we get

(47)

Then for, we have

(48)

Comparing the coefficients of and between Equation (44) and Equation (48), we get

(49)

From the definition of and Equation (49), we have

(50)

Since, we obtain

(51)

where is a constant vector. Similarly, we have

(52)

where is a constant vector. Now, we shall find the values of and. From the definition of and Equation (50), we have

(53)

and

(54)

where. In view of Equation (43), we induce that when.

(55)

Then we have

(56)

Comparing both sides of Equation (56), we obtain

(57)

where and are respectively the coefficients of and of. Thus we have

(58)

where.

Since is the eigenvalue of and is the corresponding eigenvector, we get

(59)

(60)

Therefore, substituting Equation (53) and Equation (59) into Equation (60), we have

(61)

that is

(62)

where

(63)

Thus, , and is the value of the determinant, where is formed by replacing the th column vector of by another column vector for. In a similar way, we have

(64)

where

(65)

Thus, where and is the value of the determinant that is formed by replacing the th column vector of by another column vector for. Therefore, we can determine and from Equation (51) and Equation (52). Furthermore, we can easily compute.

Then the Hopf bifurcating periodic solutions of system (1) at on the center manifold are determined by the following formulas

(66)

Here determines the direction of Hopf bifurcation. If, then the Hopf-bifurcation is forward(backward) and the bifurcating periodic solutions exist for. Again determines the stability of the bifurcating periodic solutions. The bifurcating periodic solutions are stable (unstable) if. determines the period of periodic solutions: the period increases (decreases) if. Therefore, we have the following results.

Theorem 4. The Hopf bifurcation of the system (1) occurring at when is forward (backward) if and the bifurcating periodic solutions on the center manifold are stable (unstable) if .

5. Conclusion

This paper introduces modified time-delay predator- prey model. Then we study the Hopf bifurcation and the stability of the system. Our results reveal the conditions on the parameters so that the periodic solutions exist surrounding the interior equilibrium point. It shows that is a critical value for the time delay. Furthermore, the direction of Hopf bifurcation and the stability of bifurcated periodic solutions are investigated.

Acknowledgements

This project is jointly supported by the National Natural Science Foundations of China (Grant No. 61074192). We also would like to thank the anonymous referees which have improved the quality of our study.

Cite this paper

Yang Ni,Yan Meng,Yiming Ding, (2015) Hopf Bifurcation Analysis for a Modified Time-Delay Predator-Prey System with Harvesting. Journal of Applied Mathematics and Physics,03,771-780. doi: 10.4236/jamp.2015.37094

References