Journal of Applied Mathematics and Physics
Vol.03 No.07(2015), Article ID:57628,5 pages
10.4236/jamp.2015.37092
Perturbation Solutions for Annular Flow of Small Gap
Xiaojian Cao1*, Yuefang Wang1,2
1Department of Engineering Mechanics, Dalian University of Technology, Dalian, China
2State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian, China
Email: *cxjdlut@mail.dlut.edu.cn


Received 1 April 2015; accepted 23 June 2015; published 30 June 2015

ABSTRACT
The perturbation method is used to solve the control equations of a three-dimensional annular flow inside a small gap. The nonlinear equations are separated into zeroth-order and first-order perturbation equations. The velocity and pressure distributions are solved successively by different numerical methods with the zeroth-order and first-order equation. Agreement in results is found with the present method and software ANSYS-CFX, which illustrates the applicability of perturbation method in solving complicated flow field inside small gaps.
Keywords:
Perturbation, Annular Flow, Gap, Velocity, Pressure

1. Introduction
The annular flow inside small gaps between rotors and stators can be found in many fluid circumstances such as sliding bearings, radial dynamic pressure seals, submersible pumps and nuclear pumps. The study of dynamical effects related to gap fluid field has been one of the research hotspots of fluid mechanics. Fritz [1] investigated the dynamics model of an annular flow with large gap and simplified it to a two-dimensional incompressible fluid flow field. However, this model suffered from a disadvantage that it ignored the impact of the axial flow of the fluid. Hirs [2] proposed the theory of the turbulence overall flow which was applied to investigate the three- dimensional turbulent flow field of a seal ring by Childs [3]. Nelson [4] believed Moody wall friction coefficient equations [5] were more reasonable than Hirs wall friction coefficient equations in the study of the annular flow with gap. Antunes [6] studied the static and dynamic characteristics of an annular eccentric rotor with large gap based on the overall flow theory and Hirs wall friction coefficient equation. Moody wall friction coefficient equations are widely applied in the study of the dynamics of the seal ring subjected to the radial pressure. Sun [7] proposed the dynamic modeling of a 3D annular flow with large gap using the overall flow.
In this study, the perturbation method is used to solve three-dimensional control equations of an annular fluid flow inside a small gap that separates a rotating shaft and a fixed stator. The equations are expanded into zeroth- order and first-order perturbation equations of small eccentricity. The velocity and pressure distribution for the flow domain are solved successively with the zeroth-order and first-order equations by difference methods.
2. Control Equations for Flow
Consider a small-sized control volume, CV, shown in Figure 1, across a fluctuating gap thickness, with the whole boundary CS. The continuity equation and the momentum equation of three-dimensional annular flow of a small gap can be written as:
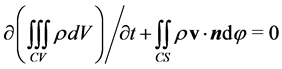 (1)
(1)
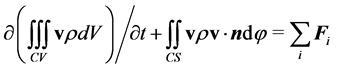 (2)
(2)
where  is fluid volume mass,
is fluid volume mass, 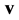 is the velocity of the fluid crossing CS,
is the velocity of the fluid crossing CS, 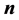 is the local unit vector normal to the boundary.
is the local unit vector normal to the boundary. 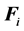 is the external and volume force acting on the fluid in CV.
is the external and volume force acting on the fluid in CV.
The control equations can be expressed based on overall flow theory and Moody’s wall friction coefficient equations [5]:
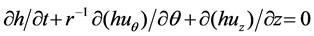 (3)
(3)
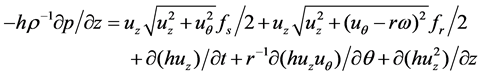 (4)
(4)
 (5)
(5)
3. Perturbation Expression
For nonlinear ordinary and partial differential equations, perturbation methods can be used to quantify the change in solution with respect to unperturbed linear systems due to tiny disturbance to parameters. These methods have been used and developed in various fields with different backgrounds [8]-[10].
The eccentricity of the rotor shaft is defined as the small disturbance in this study. The thickness of the gap, the pressure and velocity of the annular flow are assumed to be:
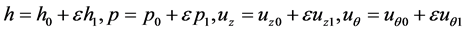 (6)
(6)
where 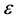 is the small parameter, being small eccentricity of the shaft centroid in this study.
is the small parameter, being small eccentricity of the shaft centroid in this study.
Equations (3) through (5) are separated in terms of order of , giving zeroth-order and first-order perturbation equations. The zeroth-order perturbation equations are as follows:
, giving zeroth-order and first-order perturbation equations. The zeroth-order perturbation equations are as follows:
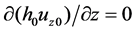 (7)
(7)
 (8)
(8)
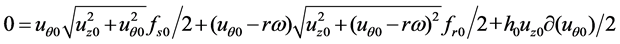 (9)
(9)
Figure 1. Geometry of the annular flow of gap.
The first-order perturbation equations are:
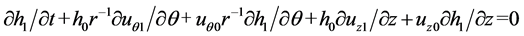 (10)
(10)


where

The difference method is used to discretize the zeroth-order perturbation equations. The nonlinear partial differential equations are transformed into algebraic equations. The zeroth-order solution is substituted into the first-order perturbation equations to obtain the solution of the first order. The results of Equations (3) through (5) are the addition of zeroth-order perturbation solutions to Equations (7) through (9) and the first-order perturbation solutions to Equations (10) through (12).
4. Results of the Flow Field
Numerical simulations using software ANSYS-CFX [11] are carried out to verify the perturbation solution obtained from the present method. An example is illustrated with boundary conditions of a 5 m/s velocity at inlet and a zero pressure at outlet. The results of pressure and circumferential velocity obtained through the perturbation equations are compared with those obtained through ANSYS-CFX, as illustrated in Figure 2 and Figure 3.
The results displayed in Figure 2(a) are the solution to the zeroth-order perturbation equations. It is noticed that the pressure distribution is axially symmetric. The closer of a position to the inlet is, the greater its pressure will be, which is qualitatively consistent with the results through ANSYS-CFX shown in Figure 2(b). Similarly, the circumferential velocity obtained through the zeroth-order perturbation equations in Figure 3 shows the same trend with those calculated by ANSYS-CFX. The profile of velocity is also centrosymmetric, and the farther to the inlet is, the greater the circumferential velocity will be. The solutions to the first-order perturbation,

Figure 2. Comparison of pressure distribution. (a) Perturbation solution; (b) ANSYS-CFX.

Figure 3. Comparison of circumferential velocity distribution. (a) Perturbation method; (b) ANSYS-CFX.
equations also agree well with the results through ANSYS-CFX qualitatively which will not be discussed any further.
5. Conclusion
The solution to a three-dimensional annular flow inside a small gap between rotor and stator is obtained using zeroth-order and first-order perturbed control equations. The perturbed solutions are compared with the numerical results through ANSYS-CFX and they are found to agree qualitatively. Consequently, it is applicable to solve three-dimensional nonlinear control equations of the small-gap annular fluid when the eccentricity of axis is small enough compared with the average clearance between the rotor and the stator.
Acknowledgements
This paper is sponsored by the National Basic Research Program of China (Grant 2015CB057300), the Key Specific Projects of Liaoning Scientific Innovation (201303002), Liaoning Provincial Science and Technology Programs(2014010499-301), Program of Cultivated Key Project of Dalian University of Technology, and the Free Exploration Project of State Key Laboratory of Structural Analysis for Industrial Equipment (S14204).
Cite this paper
Xiaojian Cao,Yuefang Wang, (2015) Perturbation Solutions for Annular Flow of Small Gap. Journal of Applied Mathematics and Physics,03,761-765. doi: 10.4236/jamp.2015.37092
References
- 1. Fritz, R.J. (1970) The Effects of an Annular Fluid on the Vibrations of a Long Rotor, Part 1-Theory. Journal of Basic Enginneering, 1970, 923-929. http://dx.doi.org/10.1115/1.3425165
- 2. Hirs, G.G. (1973) A Bulk-Flow Theory for Turbulence in Lubrication Film. ASME Journal of Lubrication Technology, 95, 137-146. http://dx.doi.org/10.1115/1.3451752
- 3. Childs, D.W. (1983) Dynamic Analysis of Turbulent Annular Seals Base on Hirs’ Lubrication Equation. ASME Journal of Lubrication Technology, 105, 429-436. http://dx.doi.org/10.1115/1.3254633
- 4. Nelson, C.C. (1987) Comparison of Hirs’ Equation with Moody’s Equation for Determining Rotor Dynamic Coefficients of Annular Pressure Seals. ASME Journal of Trilogy, 109, 144-148. http://dx.doi.org/10.1115/1.3261306
- 5. Massey, B.S. and Smith, J.W. (1979) Mechanics of Fluids. 4th Edition, Van Nostrand Reinhold Company, New York.
- 6. Antunes, J. (1996) Dynamics of Rotors Immersed in Eccentric Annular Flow. Part 1: Theory. Journal of Fluids and Structures, 10, 893-918. http://dx.doi.org/10.1006/jfls.1996.0058
- 7. Sun, Q.G. and Yu, L. (2000) Effect of Stator and Rotor Wall Roughness on Dynamic Coefficients of Eccentric Rotor in Large Gap Annular Flow. Tribology, 20, 365-369.
- 8. Chen, J.Y. (1995) An Improved Perturbation Method for Free Vibration Analysis. Journal of Sound and Vibration, 180, 519-523. http://dx.doi.org/10.1006/jsvi.1995.0094
- 9. Stepanova, L.V. and Igonin, S.A. (2014) Perturbation Method for Solving the Nonlinear Eigenvalue Problem Arising from Fatigue Crack Growth Problem in a Damaged Medium. Applied Mathematical Modeling, 38, 3436-3455. http://dx.doi.org/10.1016/j.apm.2013.11.057
- 10. Wang, Z.X. and Qiao, P. (2015) Vibration Analysis of Laminated Composite Plates with Damage Using the Perturbation Method. Composites: Part B, 72, 160-174. http://dx.doi.org/10.1016/j.compositesb.2014.12.005
- 11. Pu, G.Y. (2011) ANSYS Workbench 12 Basic Tutorial and Example Explanation, China Waterpower Press, Beijing. (In Chinese)
NOTES
*Corresponding author.





