Journal of Applied Mathematics and Physics
Vol.03 No.07(2015), Article ID:57613,4 pages
10.4236/jamp.2015.37091
Existence and Multiple of Positive Solution for Nonlinear Fractional Difference Equations with Parameter
Youji Xu
Department of Mathematics, Northwest Normal University, Lanzhou, China
Email: xuyj@nwnu.edu.cn


Received 31 March 2015; accepted 23 June 2015; published 30 June 2015

ABSTRACT
Let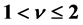 ,
,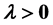 . We study the existence and multiple positive solutions of n-th nonlinear discrete fractional boundary value problem of the form
. We study the existence and multiple positive solutions of n-th nonlinear discrete fractional boundary value problem of the form 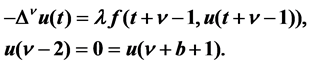 By using a fixed-point theorem on cone, the parameter intervals of problem is established.
By using a fixed-point theorem on cone, the parameter intervals of problem is established.
Keywords:
Fractional Difference Equations, Parameter Intervals, Positive Solution, Fixed-Point Theorem

1. Introduction
There have been of great interest recently on fractional difference equations. It is caused by the development of the theory of fractional calculus and discrete fractional calculus, also by its applications, see [1]-[7]. We noted that most papers on discrete fractional difference equation are devoted to solvability of linear initial fractional difference equations [8] [9]. Recently, there are some papers dealing with the existence of solutions of nonlinear boundary value problems, we also refer the readers to [10] [11]. However, there are few papers consider parameter intervals of fractional difference boundary value problems. In the present work, our purpose is to the parameter intervals of the following fractional difference boundary value problem
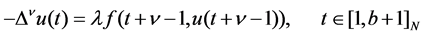 (1.1)
(1.1)
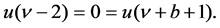 (1.2)
(1.2)
where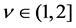 ,
, 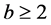 is an integer,
is an integer, 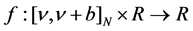 is continuous,
is continuous, 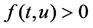 for
for 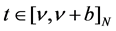 and
and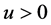 . For
. For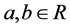 , define
, define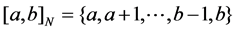 .
.
F. M. Atici and P. W. E. [10] studied fractional difference boundary value problem
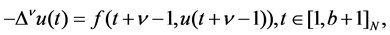 (1.3)
(1.3)
with the boundary value condition (1.2). By using Krasnosel’skii fixed point theorem under condition
(H1)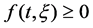 ,
,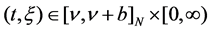 ;
;
(H2)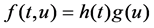 , where
, where 

(H3)


They get the following.
Theorem 1.1[10] Assume that conditions (H1) and (H2) are satisfied, then problem (1.1) and (1.2) has at least one solution. Assume that conditions (H1) and (H3) are satisfied, then problem (1.1) and (1.2) has at least one solution.
The following conditions will be used in the paper
(A1)




(A2)
2. Preliminaries
Recall the factorial polynomial 





is a pole of the Gamma function and 








where

where 



Lemma 2.1 [10] Let


is 

Lemma 2.2 [10] The Green’s function 
(i) 


(ii) 

(iii) There exists a positive number 

where

In the rest of the paper, we will use the fixed point index theory in cones to deal with (1.1) and (1.2).
Lemma2.3 [12] Let 





(i)



(ii)


holds, then 

We will need the following notations. Let
Then 
So, 


Note









Lemma 2.4 Suppose that conditions (A1) hold, and there exist two different positive numbers 



Then, problem (1.1), (1.2) has at least one positive solution 

Proof. We can suppose that



these mains that for




these mains that for






so 





3. Main Results
For some
By using Lemma 2.4, we get
Theorem 3.1 Assume that (A1) hold, and 



Theorem 3.2 Assume that (A1) hold, and 


Theorem 3.3 Assume that (A1) hold, and 


Theorem 3.4 Assume that (A1) and (A2) hold, and 


Acknowledgements
Author was supported by the NSF of Gansu Province (No. 2013GS08288).
Cite this paper
Youji Xu, (2015) Existence and Multiple of Positive Solution for Nonlinear Fractional Difference Equations with Parameter. Journal of Applied Mathematics and Physics,03,757-760. doi: 10.4236/jamp.2015.37091
References
- 1. Miller, K.S. and Ross, B. (1988) Fractional Difference Calculus. Proceedings of the International Symposium on Univalent Functions, Fractional Calculus and Their Applications, Nihon University, Koriyama, 139-152; Ellis Horwood Ser. Math. Appl., Horwood, Chichester, 1989.
- 2. Agrawal, O.P. (2002) Formulation of Euler-Lagrange Equations for Fractional Variational Problems. Journal of Mathematical Analysis and Applications, 272, 368-379. http://dx.doi.org/10.1016/S0022-247X(02)00180-4
- 3. Podlubny, I. (1999) Fractional Differential Equations. Academic Press, New York.
- 4. Lakshmikantham, V. and Vatsala, A.S. (2008) Basic Theory of Fractional Differential Equations. Nonlinear Analysis: Theory, Methods & Applications, 69, 2677-2682. http://dx.doi.org/10.1016/j.na.2007.08.042
- 5. Bai, Z. and Lü, H. (2005) Positive Solutions for Boundary Value Problem of Nonlinear Fractional Differential Equation. Journal of Mathematical Analysis and Applications, 311, 495-505. http://dx.doi.org/10.1016/j.jmaa.2005.02.052
- 6. Salem, H.A.H. (2009) On the Fractional Order m-Point Boundary Value Problem in Reflexive Banach Spaces and Weak Topologies. Journal of Computational and Applied Mathematics, 224, 567-572. http://dx.doi.org/10.1016/j.cam.2008.05.033
- 7. Atici, F.M. and Eloe, P.W. (2007) A Transform Method in Discrete Fractional Calculus. International Journal of Difference Equations, 2, 165-176.
- 8. Goodrich, C.S. (2010) Continuity of Solutions to Discrete Fractional Initial Value Problems. Computers and Mathematics with Applications, 59, 3489-3499. http://dx.doi.org/10.1016/j.camwa.2010.03.040
- 9. Atici, F.M. and Eloe, P.W. (2009) Initial Value Prob-lems in Discrete Fractional Calculus. Proceedings of the American Mathematical Society, 137, 981-989. http://dx.doi.org/10.1090/S0002-9939-08-09626-3
- 10. Atici, F.M. and Eloe, P.W. (2011) Two-Point Boundary Value Problems for Finite Fractional Difference Equations. Journal of Difference Equations and Applications, 17, 445-456. http://dx.doi.org/10.1080/10236190903029241
- 11. Goodrich, C.S. (2010) Solutions to a Discrete Right-Focal Fractional Boundary Value Problem. International Journal of Difference Equations, 5, 195-216.
- 12. Guo, D. and Laksmikantham, V. (1988) Nonlinear Problems in Abstract Cones. Academic Press, London.













