Journal of Applied Mathematics and Physics
Vol.03 No.07(2015), Article ID:57577,11 pages
10.4236/jamp.2015.37090
Periodic Sequences of p-Class Tower Groups
Daniel C. Mayer
Dedicated to the memory of Emil Artin
Email: algebraic.number.theory@algebra


Received 31 March 2015; accepted 23 June 2015; published 30 June 2015

ABSTRACT
Recent examples of periodic bifurcations in descendant trees of finite p-groups with 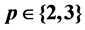 are used to show that the possible p-class tower groups G of certain multiquadratic fields K with p- class group of type
are used to show that the possible p-class tower groups G of certain multiquadratic fields K with p- class group of type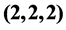 , resp.
, resp.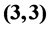 , form periodic sequences in the descendant tree of the elementary Abelian root
, form periodic sequences in the descendant tree of the elementary Abelian root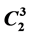 , resp.
, resp.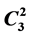 . The particular vertex of the periodic sequence which occurs as the p-class tower group G of an assigned field K is determined uniquely by the p-class number of a quadratic, resp. cubic, auxiliary field k, associated unambiguously to K. Consequently, the hard problem of identifying the p-class tower group G is reduced to an easy computation of low degree arithmetical invariants.
. The particular vertex of the periodic sequence which occurs as the p-class tower group G of an assigned field K is determined uniquely by the p-class number of a quadratic, resp. cubic, auxiliary field k, associated unambiguously to K. Consequently, the hard problem of identifying the p-class tower group G is reduced to an easy computation of low degree arithmetical invariants.
Keywords:
p-Class Field Towers, p-Principalization, p-Class Groups, Quadratic Fields, Multiquadratic Fields, Cubic Fields, Finite p-Groups, Parametrized Pc-Presentations, p-Group Generation Algorithm

1. Introduction
In this article, we establish class field theoretic applications of the purely group theoretic discovery of periodic bifurcations in descendant trees of finite p-groups, as described in our previous papers [1] [21] [22] (pp. 182-193) and [2] (§6.2.2), and summarized in section §2.
The infinite families of Galois groups of p-class field towers with 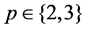 which are presented in sections §§4 and 6 can be divided into different kinds. Either they form infinite periodic sequences of uniform step size 1, and thus of fixed coclass. These are the classical and well-known coclass sequences whose virtual periodicity has been proved independently by du Sautoy and by Eick and Leedham-Green (see [1], §7, pp. 167-168). Or they arise from infinite paths of directed edges in descendant trees whose vertices reveal periodic bifurcations (see [1], Thm.21.1, p. 182, [1], Thm.21.3, p. 185, and [2], Thm.6.4). Extensive finite parts of the latter have been constructed computationally with the aid of the p-group generation algorithm by Newman [3] and O’Brien [4] (see [1] [12]-[18]), but their indefinitely repeating periodic pattern has not been proven rigorously, so far. They can be of uniform step size 2, as in §4, or of mixed alternating step sizes 1 and 2, as in §6, whence their coclass increases unboundedly.
which are presented in sections §§4 and 6 can be divided into different kinds. Either they form infinite periodic sequences of uniform step size 1, and thus of fixed coclass. These are the classical and well-known coclass sequences whose virtual periodicity has been proved independently by du Sautoy and by Eick and Leedham-Green (see [1], §7, pp. 167-168). Or they arise from infinite paths of directed edges in descendant trees whose vertices reveal periodic bifurcations (see [1], Thm.21.1, p. 182, [1], Thm.21.3, p. 185, and [2], Thm.6.4). Extensive finite parts of the latter have been constructed computationally with the aid of the p-group generation algorithm by Newman [3] and O’Brien [4] (see [1] [12]-[18]), but their indefinitely repeating periodic pattern has not been proven rigorously, so far. They can be of uniform step size 2, as in §4, or of mixed alternating step sizes 1 and 2, as in §6, whence their coclass increases unboundedly.
2. Periodic Bifurcations in Trees of p-Groups
For the specification of finite p-groups throughout this article, we use the identifiers of the SmallGroups database [5] [6] and of the ANUPQ-package [7] implemented in the computational algebra systems GAP [8] and MAGMA [9]-[11], as discussed in [1] (§9, pp. 168-169).
The first periodic bifurcations were discovered in August 2012 for the descendant trees of the 3-groups  and
and 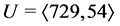 (see [1], §3, p. 163] and [1], Thm.21.3, p. 185), having abelian quotient in- variants
(see [1], §3, p. 163] and [1], Thm.21.3, p. 185), having abelian quotient in- variants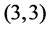 , when we, in collaboration with Bush, conducted a search for Schur
, when we, in collaboration with Bush, conducted a search for Schur 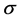 -groups as possible
-groups as possible
candidates for Galois groups 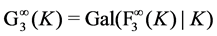 of three-stage towers of 3-class fields over complex quadratic base fields
of three-stage towers of 3-class fields over complex quadratic base fields 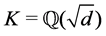 with
with 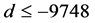 and a certain type of 3-principalization [12] (Cor. 4.1.1,
and a certain type of 3-principalization [12] (Cor. 4.1.1,
p. 775). The result in [12] (Thm. 4.1, p. 774) will be generalized to more principalization types and groups of higher nilpotency class in section §6.
Similar phenomena were found in May 2013 for the trees with roots 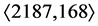 and
and 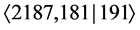 of type
of type 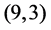 but have not been published yet, since we first have to present a classification of all metabelian 3- groups with abelianization
but have not been published yet, since we first have to present a classification of all metabelian 3- groups with abelianization .
.
At the beginning of 2014, we investigated the root
In January 2015, we studied complex bicyclic biquadratic fields

and Taous [14, Thm.2,(4)], provided the radicand d exhibits a certain prime factorization which ensures a 2- class group 

In Section §4, we use the viewpoint of descendant trees of finite metabelian 2-groups and our discovery of periodic bifurcations in the tree with root 



3. Pattern Recognition via Artin Transfers
Let p denote a prime number and suppose that G is a finite p-group or an infinite pro-p group with finite abelianization 


In this situation, there exist 
of intermediate normal subgroups 




The following information is known [16] to be crucial for identifying the metabelianization 


Definition 3.1 By the Artin pattern of 

onsisting of the multiple-layered TTT 


If 




As Emil Artin [15] pointed out in 1929 already, using a more classical terminology, the concepts transfer target type (TTT) and transfer kernel type (TKT) of a base field













derived quotient



Figure 1. Pairs 

according to the isomorphism theorem. Similarly, we have the coincidence of TKTs

4. Two-Stage Towers of 2-Class Fields
As our first application of periodic bifurcations in trees of 2-groups, we present a family of biquadratic number fields 



This claim is stronger than the statements in the following Theorem 4.1. The proof firstly consists of a group theoretic construction of all possible candidates for






Remark 4.1 Generally, the first layer of the transfer kernel type 



Theorem 4.1 Let 






Then the 2-class group 






parameters 




The Legendre symbol 



• 







of the coclass tree
• 








More precisely, in the second case the following equivalences hold in dependence on the parameters

• 



and varying

• 



and varying

We add a corollary which gives the Artin pattern of the groups in Theorem 4.1, firstly, since it is interesting in its own right, and secondly, because we are going to use its proof as a starting point for the proof of Theorem 4.1.
Corollary 4.1 Under the assumptions of Theorem 4.1, the Artin pattern 


The ordered multi-layered transfer target type (TTT) 





If we now denote by








Thus, 


Proof. The underlying order of the 7 unramified quadratic, resp. bicyclic biquadratic, extensions of 
For the TTT we use logarithmic abelian type invariants as explained in [2] (§2). 


Concerning the TKT, 


Proof. (Proof of Theorem 4.1)
Firstly, the equivalence 


Next, we use the Artin pattern of



















So far, we have been able to single out that 




is used as input for a Magma program script [10] [11] which identifies a 2-group, given by generators and relations,
Group
• CanIdentify Group() and Identify Group() if
• Is In Small Group Database(), pQuotient(), Number Of Small Groups(), Small Group() and Is Isomorphic() if
• Generatep Groups(), resp. a recursive call of Descendants() (using Nuclear Rank() for the recursion), and Is Isomorphic() if
The output of the Magma script is in perfect accordance with the pruned descendant tree
Finally, the class and coclass of 
5. Computational Results for Two-Stage Towers
With the aid of the computational algebra system MAGMA [11], we have determined the pairs of parameters




Recall that a pair 
By means of the following invariants, the statistical distribution 





The purely group theoretic pruned descendant tree was constructed in [1] (§21.1, pp. 182-184), and was shown in [1] (§10.4.1, Figure 7, p. 175), with vertices labelled by the standard identifiers in the SmallGroups Library [5] [6] or of the ANUPQ-package [7].
In Figure 1, a pair 



In Figure 2, the minimal radicand 

Vertices within the support of the distribution are surrounded by an oval. The oval is drawn in horizontal orientation for mainline vertices and in vertical orientation for vertices in other periodic coclass sequences.
6. Three-Stage Towers of 3-Class Fields
Our second discovery of periodic bifurcations in trees of 3-groups will now be applied to a family of quadratic number fields 



Theorem 6.1 Let 




resp.
Further, let the integer 
Then the 3-class field tower of 










Figure 2. Minimal radicands 


The metabelianization 






Again, we first state a corollary whose proof will initialize the proof of Theorem 6.1.
Corollary 6.1 Under the assumptions of Theorem 6.1, the Artin pattern 


The ordered multi-layered transfer target type (TTT) 




If we now denote by







Thus, 



Proof. First, we must establish the connection of the TTT of 














Now, the statements are an immediate consequence of §§4.1-4.2 in our recent article [2], where the claims are reduced to theorems in our earlier papers: [16] (Thm.1.3, p. 405), and, more generally, [18] (Thm.4.4, p.440 and Tbl.4.7, p. 441). We must only take into consideration that the 3-class group 




Proof. (Proof of Theorem 6.1) First, we use the Artin pattern of















Now, Theorem 21.3 and Corollaries 21.2-21.3 in [1] (pp. 185-187) show that, using the local notation of Corollary 21.2,
and
both with
7. Computational Results for Three-Stage Towers
With the aid of the computational algebra system MAGMA [11], where the class field theoretic techniques of Fieker [20] are implemented, we have determined the Artin pattern 



Figure 3. Minimal absolute discriminants 

precomputed by Boston, Bush and Hajir in the database underlying the numerical results in [19].
Figure 3, resp. 4, shows the minimal absolute discriminant


Figure 4. Minimal absolute discriminants 

lianization 



We have published this information in the Online Encyclopedia of Integer Sequences (OEIS) [21], sequences A247692 to A247697.
We emphasize that the results of section 6 provide the background for considerably stronger assertions than those made in [12]. Firstly, since they concern four TKTs E.6, E.14, E.8, E.9 instead of just TKT E.9 [2] (§4), and secondly, since they apply to varying odd nilpotency class 
Acknowledgements
We gratefully acknowledge that our research is supported by the Austrian Science Fund (FWF): P 26008-N25. We are indebted to Nigel Boston, Michael R. Bush and Farshid Hajir for kindly making available an unpublish- ed database containing numerical results of their paper [19].
Cite this paper
Daniel C. Mayer, (2015) Periodic Sequences of p-Class Tower Groups. Journal of Applied Mathematics and Physics,03,746-756. doi: 10.4236/jamp.2015.37090
References
- 1. Mayer, D.C. (2015) Periodic Bifurcations in Descendant Trees of Finite p-Groups. Advances in Pure Mathematics, 5, 162-195. http://dx.doi.org/10.4236/apm.2015.54020 Special Issue on Group Theory, March 2015. (arXiv: 1502.03390v1 [math.GT] 11 Feb 2015.)
- 2. Mayer, D.C. (2015) Index-p Abelianization data of p-Class Tower Groups, to appear in Advances in Pure Mathematics, 5, Special Issue on Number Theory and Cryptography, April 2015. (arXiv: 1502.03388v1 [math.NT] 11 Feb 2015.)
- 3. Newman, M.F. (1977) Determination of Groups of Prime-Power Order. In: Lecture Notes in Math., vol. 573, Group Theory, Canberra, Springer, Berlin, 73-84. http://dx.doi.org/10.1007/bfb0087814
- 4. O’Brien, E.A. (1990) The p-Group Generation Algorithm. Journal of Symbolic Computation, 9, 677-698. http://dx.doi.org/10.1016/S0747-7171(08)80082-X
- 5. Besche, H.U., Eick, B. and O’Brien, E.A. (2002) A Millen-nium Project: Constructing Small Groups. Int. J. Algebra Comput., 12, 623-644. http://dx.doi.org/10.1142/S0218196702001115
- 6. Besche, H.U., Eick, B. and O’Brien, E.A. (2005) The SmallGroups Library—A Library of Groups of Small Order. An accepted and refereed GAP 4 package, available also in MAGMA.
- 7. Gamble, G., Nickel, W. and O’Brien, E.A. (2006) ANU p-Quotient—p-Quotient and p-Group Generation Algorithms. An accepted GAP 4 package, available also in MAGMA.
- 8. The GAP Group (2015) GAP—Groups, Algorithms, and Programming—a System for Computational Discrete Algebra. Version 4.7.7, Aachen, Braunschweig, Fort Collins, St. Andrews. http://www.gap-system.org
- 9. Bosma, W., Cannon, J. and Playoust, C. (1997) The Magma Algebra System. I. The User Language. J. Symbolic Comput. 24, 235-265. http://dx.doi.org/10.1006/jsco.1996.0125
- 10. Bosma, W., Cannon, J.J., Fieker, C. and Steels, A. (eds.) (2015) Hand-book of Magma Functions. Edition 2.21, Univ. of Sydney, Sydney.
- 11. The MAGMA Group (2015) MAGMA Computational Algebra System. Version 2.21-2, Sydney. http://magma.maths.usyd.edu.au
- 12. Bush, M.R. and Mayer, D.C. (2015) 3-Class Field Towers of Exact Length 3. J. Number Theory, 147, 766-777. (arXiv: 1312.0251v1 [math.NT] 1 Dec 2013.)
- 13. Hilbert, D. (1894) Ueber den Di-richlet'schen biquadratischen Zahlk?rper. Mathematische Annalen, 45, 309-340. http://dx.doi.org/10.1007/BF01446682�
- 14. Azizi, A., Zekhnini, A. and Taous, M. (2015) Coclass of for Some Fields with 2-Class Groups of Type . To appear in J. Algebra Appl.
- 15. Artin, E. (1929) Idealklassen in Oberk?rpern und allgemeines Reziprozit?tsgesetz. Abh. Math. Sem. Univ. Hamburg, 7, 46-51. http://dx.doi.org/10.1007/BF02941159�
- 16. Mayer, D.C. (2013) The Distribution of Second p-Class Groups on Coclass Graphs. J. Théor. Nombres Bordeaux, 25, 401-456. (27th Journées Arithmétiques, Faculty of Mathematics and In-formatics, Univ. of Vilnius, Lithuania, 2011.)
- 17. Mayer, D.C. (2012) The Second p-Class Group of a Number Field. Int. J. Number Theory, 8, 471-505.
- 18. Mayer, D.C. (2014) Principalization Algorithm via Class Group Structure. J. Théor. Nombres Bordeaux, 26, 415-464.
- 19. Boston, N., Bush, M.R. and Hajir, F. (2015) Heuristics for p-Class Towers of Imaginary Quadratic Fields. To appear in Math. Annalen. (arXiv: 1111.4679v2 [math.NT] 10 Dec 2014.)
- 20. Fieker, C. (2001) Computing Class Fields via the Artin Map. Math. Comp., 70, 1293-1303.
- 21. Sloane, N.J.A. (2014) The On-Line Encyclopedia of Integer Sequences (OEIS). The OEIS Foundation Inc. http://oeis.org/















