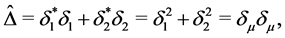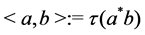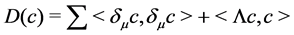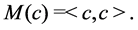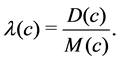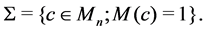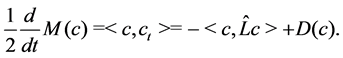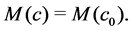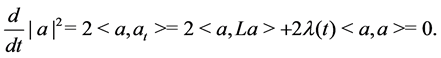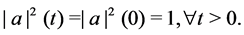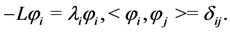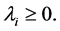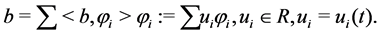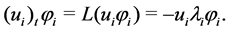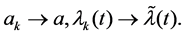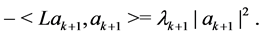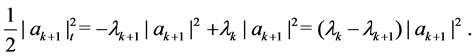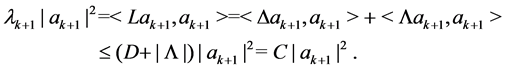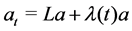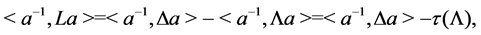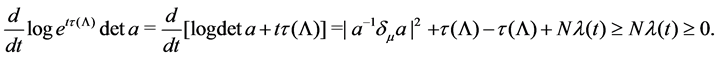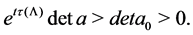Received 17 April 2015; accepted 23 June 2015; published 30 June 2015

ABSTRACT

We introduce a new L² norm preserving heat flow in matrix geometry. We show that this flow exists globally and preserves the positivity property of Hermitian matrices.

Keywords:

Global Flow, Norm Conservation, Positivity

1. Introduction

In this paper we introduce a new evolution equation in the matrix geometry such that the 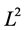norm is preserved. In [1], the author introduced the Ricci flow which exists globally when the initial matrix is a positive definite. The Ricci flow [2] [3] preserves the trace of the initial matrix and the flow converges the scalar matrix with the same trace as the initial matrix. In [4], we have introduced the heat equation, which also preserves the trace of the initial matrix. In [5]-[8], the authors introduce the norm preserving flows which are global flows and conver- ge to eigenfunctions. We know that the fidelity of quantum state is an important subject in quantum computation and quantum information [9] [10], the 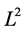norm flow we studied is very closed related to the fidelity. This is the motivation of the study of norm preserving flow in matrix geometry.

To introduce our new 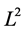norm flow in matrix geometry, we need to use some language from the book [11] and the papers [1] [4] [12]. Let 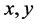be two Hermitian matrices on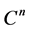. Define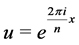,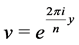. We use

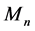to denote the algebra of all complex matrices which generated by and 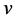with the bracket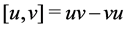. Then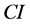, which is the scalar multiples of the identity matrix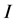, is the commutant of the operation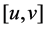. Sometimes we simply use 1 to denote the 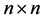identity matrix.

We define two derivations 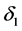and on the algebra by the commutators

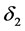
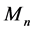
and define the Laplacian operator on 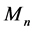by

where we have used the Einstein sum convention. We use the Hilbert-Schmidt norm 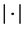defined by the inner product

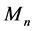
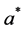
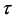
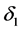
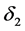
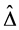
on the algebra and let. Here is the Hermitian adjoint of the matrix and denotes the usual trace function on. We now state basic properties of, and (see also [1]) as follows.

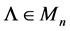
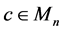
Given a positive definite Hermitian matrix. For any, we define the Dirichlet energy

and the 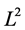mass

Let, for,

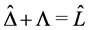
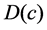
Then the eigenvalues of the operator correspond to the critical values of the Dirichlet energy on the sphere

We consider the evolution flow

(1.1)

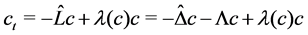
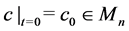
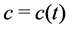
with its initial matrix. Assume is the solution to the flow above. Then

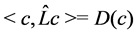
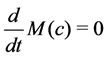
Since, we know that. Then

The aim of this paper is to show that there is a global flow to (1.1) with the initial data 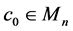and the flow preserves the positivity of the initial matrix.

2. Existence of the Global Flow

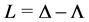
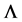
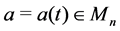
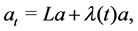
Firstly, we consider the local existence of the flow (1.1). We prefer to follow the standard notation and we let, where is a positive definite Hermitian matrix. Let be such that

(2.1)

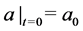
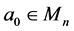
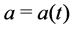
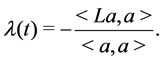
with the initial matrix. Here such that. Then for, we let

(2.2)

Formally, if the flow (2.1) exists, then we compute that

Then

In this section, our aim is to show that there is a global solution to Equation (2.1) for any initial matrix with.

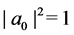
Assume at first that is any given continuous function and is the corresponding solution of (2.1). Define. Then and we get

(2.3)

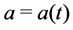
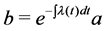
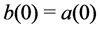
The Equation (2.3) can be solved by standard iteration method and we present it in below. Assume and are eigen-matrices and eigenvalues of as we introduced in [4], such that

Note that

Assume that 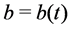is the solution to (2.3). Set

Then by (2.3), we obtain

Then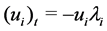, and.

Hence

and

(2.4)

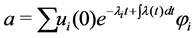
solves (2.1) with the given.

Next we define a iteration relation to solve (2.1) for the unknown 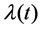given by (2.2).

Define such that it solves the equation with.

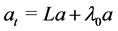
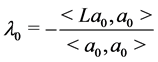
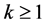
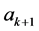
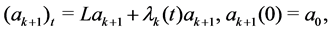
Let be any integer. Define such that

(2.5)

with

(2.6)

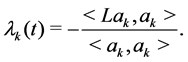
Then using the Formula (2.4), we get a sequence.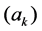

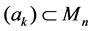
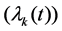
We claim that is a bounded sequence and is also a bounded sequence.

It is clear that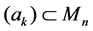. If this claim is true, we may assume

Then by (2.5) and (2.6), we obtain

and

which is the same as (2.1). That is to say, obtained above is the desired solution to (2.1).

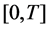
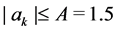
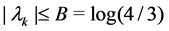
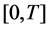
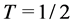
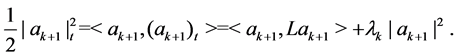
Firstly we prove the claim in a small interval. Assume and on,. Then, by (2.5),

(2.7)

By (2.6), we obtain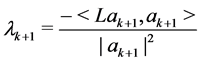. Then

By (2.7), we get

Then.

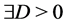
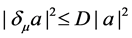
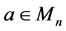
Note that such that for any. We have

Then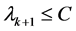. Hence the claim is true in.

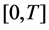
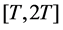
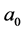
Therefore, (2.1) has a solution in. By iteration we can get a solution in with as the initial data. We can iterate this step on and on and we get a global solution to (2.1) with initial data.

In conclusion we have the below.

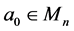
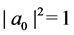
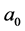
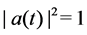
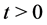
Theorem 2.1 For any given initial matrix with, the Equation (2.1) has a global solution with as its initial data and for all.

3. Positive Property Preserved by the Flow

In this section we show that positivity of the initial matrices is preserved along the flow. That is to say, we show that if the initial matrix is positive definite, then along the flow (2.1), the evolution matrix is also positive definite.

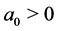
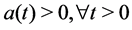
Theorem 3.1 Assume, that is is a Hermitian positive definite. Then along the flow equation

with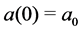, where is given by (2.2).

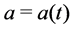
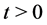
Proof. By an argument as in [4], we know is Hermitian matrix. Then we know that for small by continuity. Compute

where.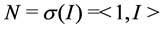

Since

and

We know that

Then we have

Hence and,.

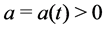
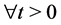
Then the proof of Theorem 3.1 is complete.

Remark that by continuity, we can show that if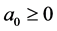, then along the flow (2.1).

Funds

The research is partially supported by the National Natural Science Foundation of China (No. 11301158, No.11271111).

Cite this paper

Jiaojiao Li,Meixia Dou, (2015) New Model for L² Norm Flow. Journal of Applied Mathematics and Physics,03,741-745. doi: 10.4236/jamp.2015.37089

References