Journal of Applied Mathematics and Physics
Vol.03 No.07(2015), Article ID:57569,7 pages
10.4236/jamp.2015.37087
Pullback Exponential Attractors for Nonautonomous Reaction Diffusion Equations in 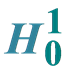
Yongjun Li, Yanhong Zhang, Xiaona Wei
School of Mathematics, Lanzhou City University, Lanzhou, China
Email: li_liyong120@163.com


Received 1 March 2015; accepted 23 June 2015; published 30 June 2015

ABSTRACT
Under the assumption that 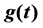 is translation bounded in
is translation bounded in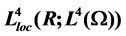 , and using the method developed in [3], we prove the existence of pullback exponential attractors in
, and using the method developed in [3], we prove the existence of pullback exponential attractors in 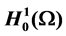 for nonlinear reaction diffusion equation with polynomial growth nonlinearity(
for nonlinear reaction diffusion equation with polynomial growth nonlinearity(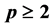 is arbitrary).
is arbitrary).
Keywords:
Dynamical System, Pullback Exponential Attractors, Reaction Diffusion Equation

1. Introduction
Attractor’s theory is very important to describe the long time behavior of dissipative dynamical systems generated by evolution equations, and there are several kinds of attractors. In this article, we will study the existence of pullback exponential attractors (see [1]-[3]) for nonlinear reaction diffusion equation. This equation is written in the following form:
 (1.1)
(1.1)
where 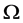 is a bounded smooth domain in
is a bounded smooth domain in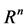 ,
, 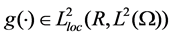 ,
, 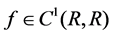 and there exist
and there exist 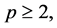
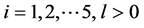
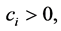 such that
such that
 (1.2)
(1.2)
for all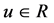 .
.
The Equation of (1.1) has been widely studied. For the autonomous case, i.e., 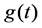 does not depend on the time, the asymptotic behaviors of the solution have been studied extensively in the framework of global attractor, see [4]-[6]. For the nonautonomous case, the asymptotic behaviors of the solution have been studied in the framework of pullback attractor, see [7]-[9]. Recently, the theory of pullback exponential attractor have been developed, see [1]-[3], and some methods are given to prove the existence of pullback exponential attractors.
does not depend on the time, the asymptotic behaviors of the solution have been studied extensively in the framework of global attractor, see [4]-[6]. For the nonautonomous case, the asymptotic behaviors of the solution have been studied in the framework of pullback attractor, see [7]-[9]. Recently, the theory of pullback exponential attractor have been developed, see [1]-[3], and some methods are given to prove the existence of pullback exponential attractors.
In order to obtain the existence of pullback exponential attractors of (1.1), we will need the following theorem.
Theorem 1.1. ([3]) Let 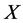 be an uniformly convex Banach space,
be an uniformly convex Banach space, 





(1) There exists an uniformly bounded absorbing set




(2) There exist




for all 









2. Some Estimates of Equation (1.1)
In this section, we will derive some priori estimates for the solutions of (1.1) that will be used to construct pullback exponential attractors for the problem (1.1).
For convenience, hereafter let 












For the initial value problem (1.1), we know from [4]-[6] that for any initial datum


Thanks to the existence theorem, the initial value problem is equivalent to a process 

In addition, we assume that the function 


By (2.1), for

Lemma 2.1. ([7]-[9]) Assume that 



and

Lemma 2.2. Assume that 


Obviously, for any bounded




Proof. Let



Taking inner product of (1.1) with 


Multiply (1.1) by
since

Combining (2.7), we get

Thanks to Poincaré inequality

Let

which imply

integrating, we get

using (2.3) and (2.4), we get the inequality (2.5).
Lemma 2.3. Assume that 


Here 

By the assumption (2.1) and for

Proof. Multiply (1.1) with

By (1.2) and Young’s inequality, we have


By (2.13), we get
integrating and using (2.4), we get

Multiply (1.1) with

By (2.1), we get

Using Young’s inequality

By the above inequality, we have
integrating and using (2.12) and (2.14), we get (2.11) holds.
Lemma 2.1, lemma 2.2 and lemma 2.3 show that the process generated by the equation (1.1) have an uniformly pullback bounded absorbing set in
Theorem 2.4. Assume that 






In fact, using the same proof as in Lemma 2.3, we can get the following result.
Lemma 2.5. Assume that 




an uniformly pullback bounded absorbing set




3. Pullback Exponential Attractors
In this section, we will use Theorem 1.1 to prove that the process generated by Equation (1.1) exists a pullback exponential attractor.
First we assume that the function 




Obviously, 



We set














Theorem 2.4. Assume that 


Next, we will verify that the process generated by (1.1) satisfy all the conditions of Theorem 1.1.
Proof. By Theorem 2.4, there exists







We set









Taking inner product of (3.2) with 


Taking into account (1.2) and Holder inequality, it is immediate to see that

and
By Lemma 2.5, we get

Using (3.3), we obtain

Let






Taking into (3.4) account, we obtain

Using the Poincaré inequality



Let



Since


By Gronwall’s lemma, we get

By (3.1), we obtain that there exists








Let

Since





By Theorem 2.4 and (3.9)-(3.11), we know that the process 
Funds
This work was supported by the National Nature Science Foundation of China (11261027) and Longyuan youth innovative talents support programs of 2014, and the innovation Funds of principal (LZCU-XZ2014-05).
Cite this paper
Yongjun Li,Yanhong Zhang,Xiaona Wei, (2015) Pullback Exponential Attractors for Nonautonomous Reaction Diffusion Equations in H01. Journal of Applied Mathematics and Physics,03,730-736. doi: 10.4236/jamp.2015.37087
References
- 1. Langa, J., Miranville, A. and Real, J. (2010) Pullback Exponential Attractors. Discrete and Continuous Dynamical Systems—Series A, 26, 1329-1357.
- 2. Czaja, R. and Efendiev, M. (2011) Pullback Exponential Attractors for Non-Autonomous Equations, Part I: Semilinear parabolic Problems. Journal of Mathematical Analysis and Applications, 381, 748-765. http://dx.doi.org/10.1016/j.jmaa.2011.03.053
- 3. Li, Y., Wang, S. and Zhao, T. (2015) The Existence of Pullback Exponential Attractors for Non-Autonomous Dynamical System and Application to Non-Autonomous Reaction Diffusion Equations. J. Appl. Anal. Comp (in press).
- 4. Chepyzhov, V. and Vishik, M. (2002) Attractors for Equations of Mathematics Physics. 49, American Mathematical Society Colloquium Publications, AMS.
- 5. Temam, R. (1997) Infinite-Dimensional Dynamical Systems in Mechanics and Physics. 68, Springer, New York. http://dx.doi.org/10.1007/978-1-4612-0645-3
- 6. Ladyzhenskaya, O. (1991)Attractors for Semigroups and Evolution Equations. Cambridge University Press, Cambridge, UK. http://dx.doi.org/10.1017/CBO9780511569418
- 7. Song, H. and Wu, H. (2007) Pullback Attractor for Nonlinear Autonomous Reaction Diffusion Equations. Journal of Mathematical Analysis and Applications, 325, 1200-1215. http://dx.doi.org/10.1016/j.jmaa.2006.02.041
- 8. Song, H. (2010) Pullback Attractors of Nonautonomous Reaction Diffusion Equation in . Journal of Differential Equations, 249, 2357-2376. http://dx.doi.org/10.1016/j.jde.2010.07.034
- 9. Li, Y. and Zhong, C. (2007) Pullback Attractors for the Norm-to-Weak Continuous Process and Application to the Non-Autonomous Reaction Diffusion Equations. Appl. Math. Comp., 190, 1020-1029. http://dx.doi.org/10.1016/j.amc.2006.11.187
- 10. Lu, S., Wu, Q. and Zhong, C. (2005) Attractors for Nonautonomous 2D Navier-Stokes Equation with Normal External Forces. Discrete Cont. Dyna. Syst, 13, 701-719. http://dx.doi.org/10.3934/dcds.2005.13.701









