Received 6 February 2015; accepted 23 June 2015; published 30 June 2015

ABSTRACT

In this paper, we provide a new approach to study the geometry of attractor. By applying category, we investigate the relationship between attractor and its attraction basin. In a complete metric space, we prove that the categories of attractor and its attraction basin are always equal. Then we apply this result to both autonomous and non-autonomous systems, and obtain a number of corresponding results.

Keywords:

Ljusternik-Schnirelmann Category, Attractor, Attraction Basin

1. Introduction

Attractors of a given system are of crucial importance, this is because that much of longtime dynamics is represented by the dynamics on and near the attractors. It is well known that the global attractors of dynamical systems can be very complicated. The geometry can be very pathological, even in the finite dimensional situation. To have a better understanding on the dynamics of a system, it is quite necessary for us to study the topology and geometry of the attractors. In the past few decades, there appeared many studies. In [1], Kapitanski and Rodnianski studied the shape of attractors of continuous semi-dynamical systems on general metric spaces. They proved that the global attractor has the same shape as the state space. Moreover, using the results on the shape of attractors, they developed an elementary Morse theory for an attractor. Lately, the author of [2] studied the Morse theory of attractors for semiflows on complete metric spaces by constructing continuous Lyapunov functions, and he introduced the concept of critical groups for Morse sets and established Morse inequalities and Morse equations for attractors. To study the geometry of the attractors, some concepts such as Lyapunov exponents, the Hausdorff dimension and the fractal dimension were also proposed, see [3] [4] etc. Recently, in [5] author studied the geometrical property of the global attractor for a class of symmetric p-Laplacian equations by means of 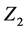index, obtained some lower estimates for the fractal dimension of the global attractor.

In this paper, by using Ljusternik-Schnirelmann category (category for short), we try to provide a new approach to studying the geometry of the global attractor. Category is a topological invariant, which often be used in the estimate of the lower bound of the number of critical points, see [6]. Here we investigate the relationship between attractor and attraction basin in the sense of category. In a complete metric space, for asymptotic compact semiflow, we obtain that the categories of attractor and attraction basin are always equal. This result match with the result in [1]. Now we can directly describe this result by category. The result will be of most interest when we choose 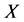be some special metric space. Finally, we have to point out that it is generally not very easy to compute the category of a given space. However, we can see there are more and more new results and methods about calculation of category, see [7] [8] etc.

We will prove the main results in Section 3 and give some applications in Section 4. Before that we provide some preliminaries and results in Section 2.

2. Preliminaries

We recall some basic definitions and facts in the theory of dynamical systems for semiflows on complete metric spaces. Let 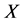be a complete metric space with metric.

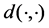Definition 2.1 A semiflow (semidynamical system) on is a continuous mapping that satisfies

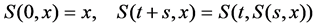for all and.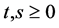

We usually write as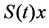. Therefore a semiflow can be viewed as a family of operators 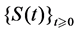satisfying:

From now on, we will always assume that there has been given a semidynamical system 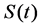on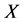; Moreover, we assume is asymptotically compact, that is, satisfies the following assumption:

For any bounded sequence and, if the sequence is bounded, then it has a convergent subsequence.

The asymptotic compactness property (A) is fulfilled by a large number of infinite dimensional semiflows generated by PDEs in application [4].

Let be a subset of. We say that attracts, if for any there exists a such that

The attraction basin of, denote by, is defined as:

The set is said to be positively invariant (resp. invariant), if

Definition 2.2 A compact set is said to be an attractor of, if it is invariant and attracts a neighborhood of itself. An attractor is said to be the global attractor of, if it attracts each bounded subset of.

Let be an open subset of, and be a closed subset of with.

Definition 2.3 A function is said to be coercive with, if for any,

In order to prove our result, we need following theorem (see Theorem 3.5 in [2]). Let there be given an attractor with attraction basin.

Theorem 2.4 ([2]) The attractor has radially unbounded Lyapunov function on such that

where is a nonnegative function satisfying

Remark 2.5 We emphasize that the is coercive with on.This point is not contained in the statement of Theorem 2.4, but we can obtain this result from the proof of the Theorem 3.5 in [2] easily.

In the following, we recall some basic results on the Ljusternik-Schnirelmann category (category for short).

Definition 2.6 Let be a topological space, be a closed subset. Set

A set is called contractible (in), if such that and one point set.

The category defined above has properties as follows.

Lemma 2.7 Properties for the category:

1);

2) (Monotonicity);

3) (Subadditivity);

4) (Deformation nondecreasing) If is continuous such that, then

;

5) (Continuity) If is compact, then there is a closed neighborhood of such that

and;

6) (Normality).

For the proof of this lemma, we refer readers to [6].

Remark 2.8 By (2) and (5), we can easily obtain that if is compact, then there exists a -neighborhood of, such that.

Just by the definition of category, we can prove the following lemma:

Lemma 2.9 Let are topology spaces, and. F is a subset of. If, then

3. Category of Attractor

The main results can be stated as follows:

Theorem 3.1 Let be a complete metric space and is a semiflow on, which is asymptotically compact. Let be an attractor of on with attraction basin. Then.

Proof. Since, by monotonicity,

. (3.1)

Since is compact, by continuity (Remark 2.8}), fixed small enough, we have

(3.2)

If we find a set such that

(3.3)

by using monotonicity again and (3.2}), we have

(3.4)

Then combine (3.1}) and (3.4), we will obtain the result

Now the rest of the work in this proof is in finding the appropriate set, which is subset of and satisfies (3.3). In order to obtain the proper set, the key tool here is the level set of Lyapunov function on attractor. Thanks to Theorem 2.4, we can construct a Lapunov function. For, we devote by the level set of in,

is clearly positively invariant and satisfies as.

By the Remark 2.5, is coercive with, that is for the fixed above, there exists such that

Hence, let, we have.

We use the method in [2], Define a function on as

Here and is continuous on. (See Theorem 5.1 and Lemma 5.2 in [2], in which replaced by.) Define

Then satisfies:

Since is continuous on, we see that is a continuous mapping, by deformation nondecreasing and monotonicity, we have

Now we just let, which completes the proof.

Now to extend our result to non-autonomous case, we consider a skew-product system, which consists of a base semiflow, and a semiflow on the phase space that is in some sense driven by the base semiflow. More precisely, the base semiflow consists of the base space, which we take to be a metric space with metric, and a group of continuous transformations from into itself such that; for all.

The dynamics on the phase space is given by a family of continuous mappings

satisfy the cocycle property

1) for all;

2) for all and;

3) is continuous.

Then we can define an autonomous semigroup on by setting

If we assume that the autonomous semigroup is asymptotically compact on, and has an global attractor, then we can generalize Theorem 3.1 to the non-autonomous case as follows:

Corollary 3.2 Let is a asymptotically compact semiflow on. If is a global attractor of on. Then.

4. Applications

In this section, we further apply our results to some special metric space, we will see some interesting results.

Example 1. Assume. Let is a asymptotically compact semiflow on. If is a global attractor of on. Then.

Proof. Suppose the contrary. Then there exist at least one point such that. Then we deduce that. By the monotonicity, we have

Note that is a punctured -dimensional sphere,

Thus, we have

On the other hand, by virtue of Theorem, we have which leads to a contradiction! Hence, the global attractor must be phase space itself.

Using similar arguments, one can prove the case of.

Example 2. In skew-product flow case, we assume. Let is a asymptotically compact semiflow on. If is a global attractor of on. Then.

Proof. Suppose the contrary. Then there exist at least one point such that. Then we deduce that. By the monotonicity, we have

Note that is a punctured - dimensional ball,

By Lemma 2.9, while by Theorem 15 in [7], we have

Thus, we have

On the other hand, by Virtue of Theorem 3.1, we have which leads to a contradiction! Hence, we obtain.

Remark 3.3 If, since

and

we can obtain the same result.

Remark 3.4 By Theorem 15.7 in [9], if is a global attractor of on. Then with is the pullback attractor of the skew-product flow, where is the section of over. Since corollary 3.2, we can show that the pull back attractor of the skew-product flow must be.

Acknowledgements

This work was supported by the National Nature Science Foundation of China (11261027) and Longyuan youth innovative talents support programs of 2014, and by the innovation Funds of principal (LZCU-XZ2014-05).

Support

This work was supported by the National Nature Science Foundation of China (11261027) and Longyuan youth innovative talents support programs of 2014, and by the innovation Funds of principal (LZCU-XZ2014-05).

Cite this paper

Jinying Wei,Yongjun Li,Mansheng Li, (2015) Category of Attractor and Its Application. Journal of Applied Mathematics and Physics,03,725-729. doi: 10.4236/jamp.2015.37086

References