Low Carbon Economy, 2015, 6, 64-72
Published Online June 2015 in SciRes. http://www.scirp.org/journal/lce
http://dx.doi.org/10.4236/lce.2015.62008
How to cite this paper: Zhang, Q. and Mei, D.X. (2015) An Empirical Research on Interactive Relationship of Urban Housing
Prices in China: Analysis of Six Major Cities. Low Carbon Economy, 6, 64-72. http://dx.doi.org/10.4236/lce.2015.62008
An Empirical Research on Interactive
Relationship of Urban Housing Prices in
China: Analysis of Six Major Cities
Qian Zhang, Dexiang Mei*
School of Economics and Management, Southwest Jiaotong University, Chengdu, China
Received 25 May 2015; accepted 21 June 2015; published 24 June 2015
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Abstract
This paper applies non-linear granger causality test and impulse response function method to
analyze the spillover effect of housing prices fluctuation among six major Chinese cities, namely,
Beijing, Shanghai, Guangzhou, Shenzhen, Tianjin and Chongqing. Results indicate that fluctuation
of urban housing prices in the short term is a wide range of positive spillover effect, and then the
effect will gradually disappear. The spillover effect of housing prices fluctuation and cities’ space
distance do not necessarily exist relationship; at the same time, Shanghai housing price fluctua-
tion has a great influence on other cities generally. Accordingly, relevant policy sugges tions are
put forward.
Keywords
Housing Prices, Spillover Effect, Non-Linear Granger Test, Impulse Response Function
1. Introduction
Real estate industry drives relevant industries at a strong degree, plays an important role in driving China’s eco-
nomic development and improves people’s living standard. The level of real estate price not only determines
whether the real estate industry can develop healthily, but also has an impact on relative industry development,
economic development, resident life quality, country financial security, etc. In particular, it will have a huge
impact on social fairness and stability.
Since 1998, when the real estate industry carried out market-oriented reform, China’s real estate industry has
always maintained the rapid development of strength. At the same time, housing prices generally present the fast
*
Corresponding author.

Q. Zhang, D. X. Mei
65
growth momentum. In 2014, the growth of many cities’ housing prices slows down or even falls, which once
again inspires people to debate whether the real estate market enters a turning point. These cities’ housing prices’
changes will affect housing prices fluctuation of other areas or not, whether there are internal relations among
housing prices’ fluctuation of different areas, and whether it is affected by a certain mechanism is worth explor-
ing.
2. Literature Review
In existing literature, the earliest scholar who researched the fluctuation relationship of house prices was Hol-
mans [1], analyzed and calculated the 90s and 1960s’ British regional housing prices, found the propensity for
housing prices to change first predominantly London in the south of the country and gradually impacted from
south to north across the UK housing prices fluctuations, and defined it as the “ripple effect” of housing prices.
“ripple effect” was a kind of special form of housing prices fluctuation spillover effect, it indicated the
long-term relationships that some areas’ housing price fluctuations drived by the center city/core region and
have a conduction effect on other cities/regions’ housing prices fluctuations. Among other scholars research on
housing prices, a similar phenomenon was called diffusion effect, space effect or ripple effect. In this article, this
kind of phenomenon was called “housing prices fluctuation spillover effect”, namely, the housing market prices
fluctuation of a region would affect another region prices fluctuations.
In recent years, domestic and foreign scholars used different methods to research and explore real estate price
fluctuation spillover effect. Hui [2] applied co-integration test and granger causality test method, found housing
prices changes exist mutual influence among three cities in Malaysia. Holly and Pesarana [3] used the spatial
econometric methods, under the condition of controlling the influence of real income and other factors, analyzed
the 49 states housing data of 29 years, found space factors still have important effects on housing prices fluctua-
tions. Bandt, Barhoumi and Bruneau [4] expanded this kind of research to the oecd member countries, suggested
that the real house prices directly or indirectly affect the prices of other countries. Lee and Chien [5] analyzed
the regional housing prices in 1993-2009 in Taiwan area by using the latest methods of unit root test. The result
showed that housing prices had significantly diffusion effect in other regions except Taipei. At the same time
deemed it is caused by a smaller public housing and the housing presale system. Simo-Kengne, Bittencourt and
Gupta [6] examined the influence of South Africa’s nine provinces prices on economic development, set up
space SUR model, showed that space effect was a very important factor to affect housing prices. Lean and
Smyth [7] investigated the relationship of the price index in Malaysia 14 regional five different building types
by using single factor and panel LM unit root test method, and found that Malaysia’s regional housing prices
passed from the most developed regions to the less developed areas. The study of Ferrari and Rae [8] considered
migration, especially the selective migration, impacted the UK housing prices space differentiation. Liu and
Roberts [9] from the perspective of counter urbanization examined interdependent relationship between the re-
gional house prices in Hong Kong by using vector error model. The results showed that the diffusion effect of
Hong Kong housing prices from city center to rural areas was greater than the inverse process of urbanization.
Zhu and other scholars [10] researched yields of non-system risk and volatility of the spacespace relationship of
19 U.S. regional housing markets in 1995-2009. The result showed that the linkage of the whole market not only
affected adjacent space regions, also affected the similar economic level region; At the same time due to the
spread of the subprime crisis, made the space influence of whole housing market more strongly.
Scholars in the study of Chinese regional housing prices fluctuation spillover was still in the exploratory stage,
mainly concentrated in the validation of whether China’s regional housing prices volatility spillover effect exists,
only a minority of scholars further study on the space diffusion path of housing prices. Liang and Gao [11] in the
perspective of regional differences found that housing prices fluctuation in the area are different. At the same
time, through empirical analysis, found that the regional price differences are mainly caused by the effect of
monetary policy and the differences in expectations of housing prices. Hong et al. [12], on the basis of panel da-
ta model, used CSD inspection to analyze the residual further, concluded that there are correlations between dif-
ferent cities real estate prices. Li [13] through IVQR and spatial econometric analysis, pointed out that urban
housing prices in China rose in the whole performance, mainly due to price changes inertia, demand-driven and
housing prices change “ripple effect”. Meanwhile, the effect of inflation would lead to less ripple effect. Wang
and Liu [14] used the impulse response function to analysis Beijing, Shanghai, Tianjin and Chongqing housing
prices data bubble and found that four cities housing prices bubble have widespread spillover effects, but had

Q. Zhang, D. X. Mei
66
significant differences in influencing direction and strength. Liang and Xing [15] utilized the dynamic factor
model to analyse housing prices fluctuation factor of 26 large and medium cities, showed that the regional cha-
racteristics of the regional factor had great influence on regional cities prices fluctuation. Simultaneously, Chi-
na’s cities prices fluctuation presented the “ripple effect”, which spread from eastern developed regions to the
central and western regions.
From the above studies both at home and abroad, foreign scholars study are more abundant. They proved that
the housing prices fluctuation spillover effect widely exists in various countries and regions through a variety of
methods. Moreover, some scholars further found that housing prices fluctuation are mostly driven by economic
or real estate developed region to undeveloped region. However, domestic related literature is relatively small,
the existing research mainly focus on the use of statistical test and space measurement method to test whether
China regional housing prices fluctuation spillover effects exist. Furthermore, specific conduction path for the
housing prices fluctuation spillover of research and analysis on domestic is almost none. Based on the above
reasons, this paper made further researches, by using DCC MVGARCH model to study dynamic correlations
among different China’s cities housing prices fluctuation and to explore the conduction relationship among
China’s cities prices fluctuation fluctuation spillover.
2.1. Research Method Introduction
2.1.1. Nonlinear Granger Test Method
Bake and Broch [16] study found that the results when using the method of linear causality test analysis in ex-
amining the nonlinear causality was not accurate. Thus, they proposed a new nonparametric statistical methods
to examine the nonlinear relationship of things by introducing the concept of spatial probability. On this basis,
Hiemstra and Jones [17] allowed variables to have weak dependence, so as to enhance the scope of the nonlinear
test method. Their proposed nonlinear Granger test is as follows.
The nonlinear Granger test is firstly assumed that the sum is two stationary time series and then defined:
Is a leading sequence m phase vector, namely, m = 1, 2, …; T = 1, 2, …
Is a sequence Lx phase vector, namely the Lx = 1, 2, …; T = Lx + 1, Lx + 2, …
Is a sequence Ly phase vector, namely Ly = 1, 2, …; T = Ly + 1, Ly + 2, …
For a given m, Lx, Ly 1 ≥ 1, and the interval parameter e > 0. Conditions of null hypothesis “Y (strict) is
not nonlinear granger reason of X” establish:
Among them, on behalf of the probability function, on behalf of the vector norm. According to the definition
of conditional probability formula and the definition of the maximum norm, the type () can be further defined:
The ratio of the joint probability distribution of the type () can be further simplified:
Makes the Kernel function is 1 when the distance of maximum norm is between variables and the variables
and falls within the scope of e, not in e is 0. So further expand the type (), can get:
Among them, using the Kernel function eliminate values of variables maximum norm which fell outside the
scope of e.
Thus, if the sequence sum is a strictly stationary and weakly dependent assumption, using the joint probability
value in the type () can convert the test of null hypothesis “Y (strict) is not nonlinear granger reason of X” in the
type () to test whether the type () is set up.
The significance of the positive test statistic in the type () indicates that the lag value of Y is good for the pre-
diction of X, but the significant negative test statistic shows that the information in the lag of Y interferes with
the prediction of X. Therefore, when test causality exists, test statistics in the type () shall be calculated accord-
ing to according to the critical value of the right tail inspection.
2.2. Data Introduction
Beijing, Shanghai, Guangzhou, Shenzhen, Tianjin and Chongqing, the six cities hold important positions in
China’s economic development and real estate industry development, the changes in these cities’ housing prices
have been received extensive attention of the society. Therefore, this paper selects the six representative cities to
study the spillover relationship of the housing prices fluctuation.
According to the availability of data, in this paper, the sample interval of empirical analysis is July 2005 to
November 2014, a total of 113 sets of data. Data is from where national bureau of statistics of China published
monthly new commodity housing sales price index in 70 large and medium cities housing prices data (Last

Q. Zhang, D. X. Mei
67
month = 100), and through simple calculation convert into the cities’ housing prices monthly rate. Table 1
shows the main descriptive statistics of the sample.
3. Empirical Analysis and Results
3.1. Unit Root Test
Before using the empirical analysis of nonlinear granger causality test, according to the Hiemstra and Jones [17]
study, the housing prices fluctuation sequence of each city need to be carried out unit root test separately at first.
The results are shown in Table 2. All time series have rejected “existence unit root” null hypothesis according to
the results of test. So the four variables that this paper need are stable, the nonlinear granger test analysis can be
further expanded.
3.2. Nonlinear Granger Causality Test
With the continuous development of nonlinear research in recent years, the existing research shows that when the
time series exist nonlinear changing trend, the traditional granger causality test may not be able to discriminate
whether there is a causal relationship of variables accurately, or lead to a significant deviation of conclusions. So,
in order to investigate the transitive relationship of the six cities’ housing prices fluctuation in Beijing, Shanghai,
Guangzhou, Shenzhen, Tianjin and Chongqing, this paper applies the nonlinear granger causality test method to
study the nonlinear relationship of cities housing prices fluctuations. To test whether there is “strictly” nonlinear
relationship in the sequence, this paper uses VAR model to conduct the sequence “linear filtering” and further test
the filtered residual sequence. In addition, results are very sensitive to the choice of lag period in causality test, so
in order to display the nonlinear relationship of the four cities’ housing prices fluctuation completely, this paper
lists results of the nonlinear granger causality test based on common lag periods () 1 to 6 in Table 3.
Table 3 shows that Beijing’s housing price fluctuation is influenced by the two cities which are Shenzhen and
Tianjin in one-way, the price fluctuations of Beijing, Guangzhou and Shanghai have a one-way causality on
Chongqing market, at the same time, the price fluctuation of Guangzhou has a striking impact on Shanghai
Table 1. Descriptive statistics data.
Beijing Shanghai Guangzhou Shenzhen Tianjin Chongqing
Mean 0.0060 0.0021 0.0044 0.0039 0.0040 0.0030
Minimum −0.0130 −0.0260 −0.0310 −0.0560 −0.0110 −0.0290
Std. Dev. 0.0090 0.0090 0.0113 0.0122 0.0059 0.0098
Skewness 1.1045 0.4138 −0.2780 −1.7573 0.6076 2.0242
Kurtosis 5.8097 4.3599 4.1211 9.7894 5.8150 14.8199
Jarque-Bera 61.2121*** 12.1440*** 7.5040** 280.0625*** 45.0466*** 747.9780***
Observations 115 115 115 115 115 115
Remarks: ***, ** and * respectively at the 1%, 5% and 10% significant level to reject the null hypothesis.
Table 2. Results of unit root test.
ADF test statistic PP test statistic
t-statistic Prob (P) Adj. t-Stat (T) Prob (P)
Beijing −2.7218* 0.0735 −3.9955*** 0.0020
Shanghai −3.6242*** 0.0067 −3.8426*** 0.0034
Guangzhou −4.6432*** 0.0002 −4.8213*** 0.0001
Shenzhen −4.3637*** 0.0006 −4.2771*** 0.0008
Tianjin −5.0403*** 0.0000 −5.3114*** 0.0000
Chongqing −4.8645*** 0.0001 −4.6532*** 0.0002
Remarks: ***, ** and * respectively at the 1%, 5% and 10% significant level to reject to exist unit root null hypothesis.

Q. Zhang, D. X. Mei
68
Table 3. Nonlinear granger causality test based on VAR linear filtering.
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Beijing Shanghai
1 0.0605* 1.5508
Shanghai Beijing
1 0.0655* 1.5099
2 0.1699 0.9544 2 0.0929* 1.3230
3 0.1863 0.8915 3 0.0746* 1.4426
4 0.2264 0.7507 4 0.1134 1.2088
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Beijing
Guangzhou
1 0.1018 1.2714
Guangzhou
Beijing
1 0.0138** 2.2028
2 0.0487** 1.6577 2 0.0109** 2.2946
3 0.0167** 2.1277 3 0.0083*** 2.3937
4 0.0416** 1.7320 4 0.0304** 1.8747
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Beijing
Shenzhen
1 0.3284 0.4443
Shenzhen
Beijing
1 0.1486 1.0423
2 0.1723 0.9452 2 0.1501 1.0359
3 0.1285 1.1335 3 0.0876* 1.3556
4 0.1627 0.9834 4 0.0888* 1.3483
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Beijing Tianjin
1 0.8162 −0.9008
Tianjin Beijing
1 0.0378** 1.7766
2 0.1788 0.9201 2 0.0129** 2.2294
3 0.2979 0.5304 3 0.0327** 1.8424
4 0.2123 0.7986 4 0.0401** 1.7490
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Beijing
Chongqing
1 0.0138** 2.2030
Chongqing
Beijing
1 0.1274 1.1389
2 0.0181** 2.0954 2 0.4412 0.1479
3 0.0395** 1.7565 3 0.3687 0.3352
4 0.0430** 1.7171 4 0.4819 0.0454
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Shanghai
Guangzhou
1 0.6437 −0.3683
Guangzhou
Shanghai
1 0.0130** 2.2255
2 0.2140 0.7927 2 0.0040*** 2.6514
3 0.2614 0.6390 3 0.0062*** 2.4995
4 0.3056 0.5084 4 0.0038*** 2.6667
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Shanghai
Shenzhen
1 0.3012 0.5208
Shenzhen
Shanghai
1 0.1193 1.1783
2 0.0378** 1.7766 2 0.1522 1.0271
3 0.0348** 1.8142 3 0.2551 0.6586
4 0.0524* 1.6217 4 0.0579* 1.5722
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Shanghai Tianjin 1 0.0299** 1.8819 Tianjin Shanghai 1 0.0845* 1.3752

Q. Zhang, D. X. Mei
69
Continued
2 0.0035*** 2.6944 2 0.1340 1.1077
3 0.0029*** 2.7575 3 0.0921* 1.3278
4 0.0153** 2.1629 4 0.0867* 1.3614
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Shanghai
Chongqing
1 0.0876* 1.3559
Chongqing
Shanghai
1 0.6513 −0.3889
2 0.0299** 1.8828 2 0.1085 1.2345
3 0.1297 1.1276 3 0.2893 0.5556
4 0.1070 1.2424 4 0.3169 0.4764
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Guangzhou
Shenzhen
1 0.0198** 2.0585
Shenzhen
Guangzhou
1 0.1567 1.0080
2 0.1042 1.2580 2 0.0176** 2.1059
3 0.0167** 2.1281 3 0.0302** 1.8784
4 0.0686* 1.4866 4 0.0244** 1.9711
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Guangzhou
Tianjin
1 0.0746* 1.4425
Tianjin
Guangzhou
1 0.1245 1.1526
2 0.1028 1.2655 2 0.1082 1.2364
3 0.0431** 1.7157 3 0.0175** 2.1074
4 0.0660* 1.5064 4 0.0875* 1.3563
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Guangzhou
Chongqing
1 0.0959* 1.3055
Chongqing
Guangzhou
1 0.5758 −0.1912
2 0.0333** 1.8345 2 0.1818 0.9087
3 0.0366** 1.7914 3 0.3411 0.4095
4 0.0356** 1.8038 4 0.1366 1.0956
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Shenzhen
Tianjin
1 0.1438 1.0636
Tianjin
Shenzhen
1 0.0924* 1.3264
2 0.3599 0.3587 2 0.0307** 1.8709
3 0.0705* 1.4721 3 0.0293** 1.8913
4 0.0519* 1.6266 4 0.0246** 1.9669
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Shenzhen
Chongqing
1 0.7757 −0.7579
Chongqing
Shenzhen
1 0.3497 0.3862
2 0.2786 0.5869 2 0.2883 0.5583
3 0.2684 0.6175 3 0.0399** 1.7521
4 0.1012 1.2748 4 0.0335** 1.8314
Null hypothesis Lx = Ly P statistics T statistics Null hypothesis Lx = Ly P statistics T statistics
Tianjin
Chongqing
1 0.0471** 1.6732
Chongqing
Tianjin
1 0.0765* 1.4293
2 0.0176** 2.1065 2 0.0468** 1.6772
3 0.0496** 1.6489 3 0.0660* 1.5064
4 0.0145** 2.1826 4 0.0683* 1.4888

Q. Zhang, D. X. Mei
70
market, Chongqing has a remarkable one-way nonlinear effect on the price fluctuations of Shenzhen. Besides,
there are significant two-way causal relationships among among other cities housing prices fluctuations.
Collectively, through the nonlinear granger causality test to investigate China’s six major cities housing prices
fluc tua tion spillover effect, can find the following characteristics: 1) there is significant spillover effect
among housing prices fluctuation; 2) the spillover effect exists is not necessarily related, may also be affected
with the space distance, may also be affected by other factors such as economic level; 3) the price fluctuation
spillover of the housing market has some asymmetry.
Because the nonlinear Granger causality test can only examine the transmission direction of cities housing
prices fluctuation spillover effect from the statistical perspective, need to further use the impulse response func-
tion to identify the impact strength and direction of the spillover effect. Impulse response function is an efficient
tool to research housing prices spillover effect. It can track the dynamic effect of each house price fluctuation
variables impact on system. The most commonly used method is to use Cholesky to decompose residual cova-
riance matrix to obtain the corresponding orthogonalization pulse, however the Cholesky decomposition results
depend heavily on the order of the variables in the model. The generalized impulse response function proposed
by Koop et al (1996) effectively overcome the above shortcomings. Therefore, we use generalized impulse re-
sponse function to investigate the regional spillover effect of residential real estate market. The result is shown
in Figure 1.
Overall, the impact of housing prices fluctuation in the six major cities is more remarkable in the short term.
However, after the eighth basically stable stage and the response almost disappear at the same time, this shows
the long-term impact of spillover effects is not obvious. Combined with the analysis of Figure 1, we found that
there is a wide spillover effect among cities housing prices fluctuations, but there are some differences in inten-
sity and direction. Firstly, the impact of housing prices fluctuation in all cities has the biggest impact on their
market, especially the influence of the former two periods impact is significant compared with other cities, but
the pace of decline is more quickly. Secondly, the impact of cities housing prices fluctuation influenced by ex-
ternal shocks in stage 2 and 3 is general maximum, then gradually decreases, and the influence gradually disap-
pear after the eighth period. So we take phase 2 and 3 as an example, report the impact of cities housing prices
fluctuation on other cities real estate market. Beijing housing market is subject to external shocks mainly from
Shanghai and Guangzhou. Shanghai housing prices fluctuation has the biggest impact on the market of Chongq-
ing. The biggest impact on the housing prices fluctuation in Shanghai is subject to the Guangzhou and Shenzhen
real estate market, followed by Beijing and Tianjin. Each city housing prices fluctuation can have a certain in-
fluence on Shanghai real estate market, but they are much smaller than the impact of prices fluctuations from
Shanghai itself. Shenzhen influenced the impact of Guangzhou housing prices fluctuation in stage 2 is maximum,
but in the third period Guangzhou, Shanghai and Chongqing have a greater impact on the housing prices fluctu-
ationin Shenzhen. The largest spillover effects of Tianjin real estate market price fluctuations in stage 2 is from
Beijing, and it is greater than the effect of its impact in Tianjin, and the Guangzhou and Shanghai housing prices
fluctuationin the third phase will also have strong impact on the Tianjin market. Finally, in addition to Chongq-
ing has a strong negative spillover effect on the Guangzhou market in the third period, there are obvious positive
spillover effects among the rest of the cities’ housing prices fluctuations.
Through the investigation, we can get the following characteristics of the six major cities housing prices fluc-
tuations: 1) the housing prices fluctuation spillover effects are more obvious in the short term; 2) the housing
prices fluctuation of Shanghai has a great influence on other cities generally, this may be related to its strong
economic development level; 3) there is significant positive spillover effect among housing prices fluctuations;
4) the biggest impact of cities housing prices fluctuation generally comes from their own.
4. Conclusions
This paper selects six major cities, namely, Beijing, Shanghai, Guangzhou, Shenzhen, Tianjin and Chongqing, as
the research object, using the nonlinear granger test and generalized impulse response function to analyze the
new commodity housing price index for monthly of six cities in July 2005 to January 2015 and to investigate the
six cities’ housing price fluctuation spillover effect.
Research shows that: 1) cities’ housing prices fluctuation in the short term is a wide range of positive spillover
effect, and then the effect will gradually disappear; 2) the spillover effect of housing prices fluctuation and ci-
ties’ space distance do not necessarily exist relationship, and may also be affected by factors such as eco-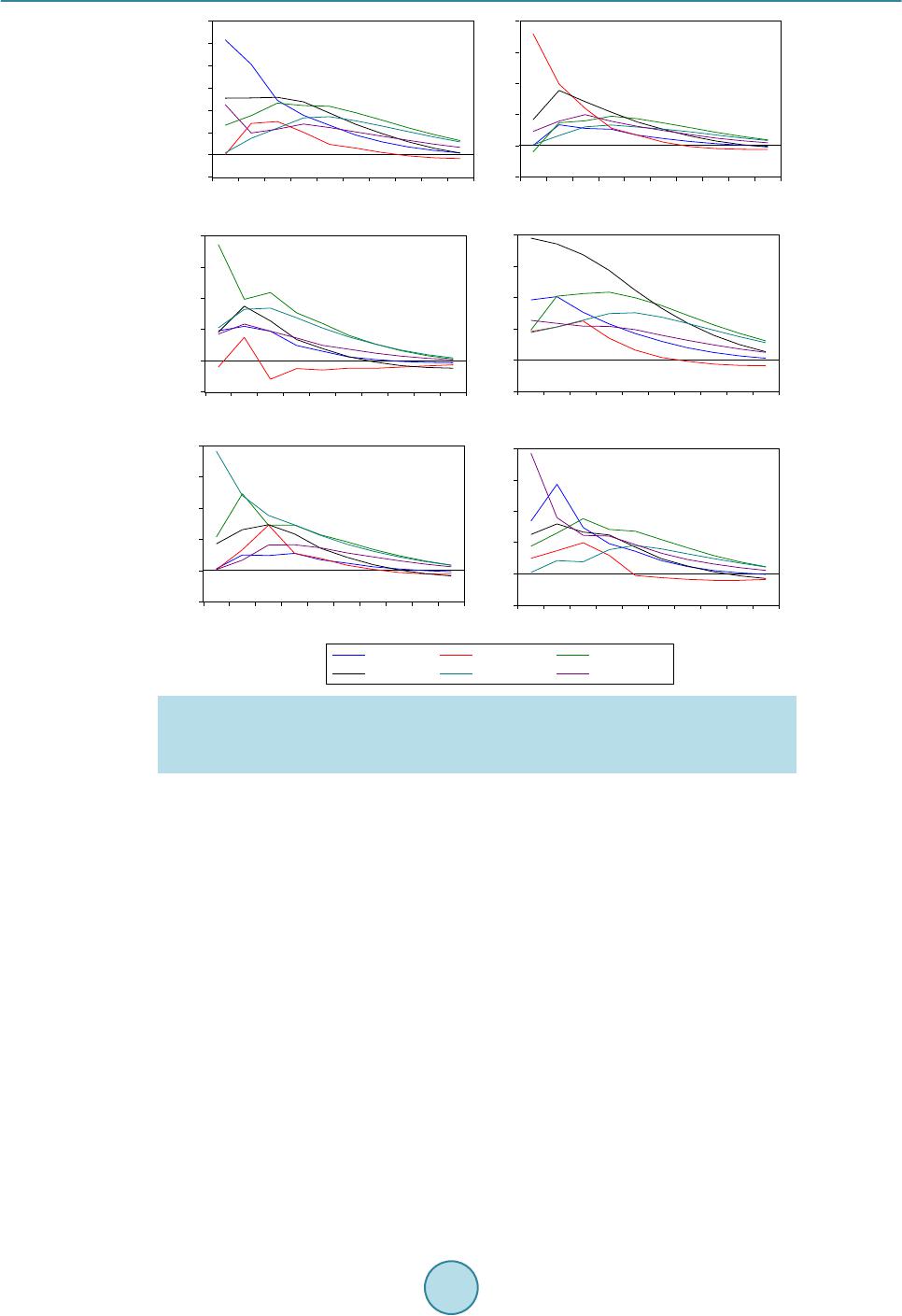

Q. Zhang, D. X. Mei
71
-.001
.000
.001
.002
.003
.004
.005
.006
12345678910
1-1
-.002
.000
.002
.004
.006
.008
123456 7 8910
1-2
-.002
.000
.002
.004
.006
.008
12345678910
1-3
-.001
.000
.001
.002
.003
.004
12345678910
1-4
-.002
.000
.002
.004
.006
.008
1 2 345678910 -.001
.000
.001
.002
.003
.004
1 2 3 4 5678910
Beijing Chongqing Guangzhou
Shanghai Shenzhen Tianjin
1-6
1-5
Figure 1. Generalized impulse response function analysis results. Remarks: 1-1, 1-2, 1-3, 1-4,
1-5, 1-6 are the generalized impulse response function graphs which represent respectively
Beijing, Chongqing, Guangzhou, Shanghai, Shenzhen, Tianjin is impacted by the other city
housing prices fluctuation compositions.
nomic development level; 3) Shanghai has a great influence on other cities generally, and this may be related to
its strong economic development level. This study is not only conducive to the relevant government departments
for the housing market macroeconomic regulation and control, regional and systemic risk prevention, but also
good for the housing market participants to risk management.
Based on the above research conclusions, this paper has the following suggestions: F i r st , the stability of the
real estate regulation and control policies should be kept as far as possible. This is beneficial to avoid sharp
fluctuations in housing prices to maintain the steady and healthy development of the real estate market; the
second is to strengthen the central government unified guidance for real estate regulation at the same time, ac-
cording to the actual situation of different areas of the real estate market development, strengthening the guid-
ance and audit of local rules for regulation and control policies, i.e. to adjust measures to local conditions to
avoid the “one size fits all”, and to prevent the local government in disguise to resist the policy of regulation; the
third is to strengthen real estate regulation and control of the areas where housing prices fluctuate dramatically
and have obvious spillover effects, to avoid that the housing price fluctuation spillover effect causes other hous-
ing markets’ fluctuation, which is beneficial to the stability of the entire housing market and the prevention of
regional and systematic real estate risks.
References
[1] Holmans, A.E. (1990) House Prices: Changes through Time at National and Sub-National Level. Department of the

Q. Zhang, D. X. Mei
72
Environment, London.
[2] Hui, H.-C. (2010) House Price Diffusions across Three Urban Areas in Malaysia. International Journal of Housing
Markets and Analysis, 3, 369-379. http://dx.doi.org/10.1108/17538271011080664
[3] Holly, S., Hashem Pesarana, M. and Yamagata, T. (2010) A Spatio-Temporal Model of House Prices in the USA.
Journal of Econometrics, 158, 160-173. http://dx.doi.org/10.1016/j.jeconom.2010.03.040
[4] De Bandt, O., Barhoumi, K. and Bruneau, C. (2010) The International Transmission of House Price Shocks. Springer,
Berlin, 129-158. http://dx.doi.org/10.1007/978-3-642-15340-2_7
[5] Lee, C.-C. and Chien, M.-S. (2011) Empirical Modelling of Regional House Prices and the Ripple Effect. Urban Stu-
dies, 48, 2029-2047. http://dx.doi.org/10.1177/0042098010385257
[6] Simo-Kengne, B.D. , Bittencourt, M. and Gupta, R. (2012) House Prices and Economic Growth in South Africa: Evi-
dence From Provincial-Level Data. Journal of Real Estate Literature, 20, 97-117.
[7] Lean, H.H. and Smyth, R. (2013) Regional House Prices and the Ripple Effect in Malaysia. Urban Studies, 50, 895-
922. http://dx.doi.org/10.1177/0042098012459582
[8] Ferrari, E. and Rae, A. (2013) The Spatiality of Housing Market Volatility and Selective Migration. Town Planning
Review, 84, 107-125. http://dx.doi.org/10.3828/tpr.2013.6
[9] Liu, N. and Roberts, D. (2013) Counter-Urbanisation, Planning and House Prices: An Analysis of the Aberdeen Hous-
ing Market Area, 1984-2010. Town Planning Review, 84, 81-105. http://dx.doi.org/10.3828/tpr.2013.5
[10] Zhu, B., Füss, R. and Rottke, N.B. (2013) Spatial Linkages in Returns and Volatilities among U.S. Regional Housing
Markets. Real Estate Economics, 41, 29-64. http://dx.doi.org/10.1111/j.1540-6229.2012.00337.x
[11] Liang, Y.-F. and Gao, T.-M. (2007) Empirical Analysis on Real Estate Price Fluctuation in Different Provinces of
China. Economic Research Journal, 8, 133-142.
[12] Hong, T., Xi, B. and Gao, B. (2007) Co-Movement of Real Estate Prices and Spatial Diffusion of Bubbles: Evidence
from 35 Metropolis in China from 2000 to 2005. Statistical Research, 24, 64-67.
[13] Li, Y.-Y. (2014) Demand Driving and Ripple Effects of Housing Prices Rising: On Strategies to Deal with the Prob-
lems of Housing Price. China Economic Quarterly, 2, 443-464.
[14] Wang, J.-Y. and Liu, X.-L. (2014) Residential Fundamental Value, Bubble Component and Regional Spillover Effect.
China Economic Quarterly, 4, 1283-1302.
[15] Liang, Y.-F. and Xing, C.-S. (2012) An Application Research on Dynamic Factor Model of Housing Prices Fluctuation:
Based on 26 Cities in China. Mathematics in Practice and Theory, 24, 7-16.
[16] Baek, E.G. and Brock, W.A. (1992) A Nonparametric Test for Independence of a Multivariate Time Series. General
Information, 2, 137-156.
[17] Hiemstra, C. and Jones, J.D. (1994) Testing for Linear and Nonlinear Granger Causality in the Stock Price-Volume
Relation. Journal of Finance, 49, 1639-1664.